地下空间增层开挖支护桩与基桩工作特性模型试验研究
孔德森,吴绍娟,马顺顺,王 凯
(1.山东科技大学 土木工程与建筑学院,山东 青岛 266590;2.山东科技大学 山东省土木工程防灾减灾重点实验室,山东 青岛 266590)
由于土地资源有限,城市规划设计缺乏创新性与前瞻性,导致部分建筑不能满足人们的多方面需求。因此,城市地下空间扩增成为缓解城市用地紧张的必要手段。既有基坑二次开挖会使原有支护桩的嵌固深度变小,进而打破原有的桩-土平衡状态。随着开挖深度的增加,既有支护桩难以承受桩后的土压力而发生倾覆破坏,从而导致基坑倒塌,造成严重的工程事故。为避免此类事故的发生,需要在既有基坑二次开挖前,在原有支护桩外侧新增一排支护桩,形成既有-新增双层排桩支护体系[1],不仅能够提高基坑支护能力,而且可以充分利用既有支护桩的承载能力,保证上部建筑物的稳定。 龚晓南等[2]采用理论分析和数值模拟方法研究了增层开挖后桩基的承载力,分析了增层开挖条件下桩侧极限摩阻力损失比随不同增层开挖宽度和深度的变化规律。伍程杰[3]利用有限元软件建立地下空间向下增层开挖的三维有限元模型,研究了群桩基础的桩身轴力、桩侧摩阻力、土体回弹等在二次开挖过程中的变化规律。单华峰等[4]采用有限元软件模拟地下空间二次开挖过程,并对群桩基础中的桩基沉降特性进行了研究,发现桩顶沉降量与地下空间二次开挖深度呈正比,当开挖深度不变时,不同位置的桩顶沉降量不同。冯若峰[5]对二次开挖过程中役桩的竖向承载特性进行研究,对比分析受荷单桩和群桩的承载特性差异,建立了在役桩的荷载传递模型。Lee等[6]利用有限元软件,对基坑内单桩和群桩的工作机理进行研究,分析了基坑开挖过程中单桩和群桩的受力、变形规律。Wan等[7-9]对基坑开挖过程中桩身拉力的产生和桩身拉力的变化规律进行了研究,认为基坑开挖的卸荷作用是导致桩身拉力产生的主要原因。王相阁等[10]通过室内大比尺模型试验,研究了h型双排桩中的既有桩与新增桩桩身受力随开挖深度的变化规律。唐德琪等[11]通过室内模型试验方法,研究了被动区土体侧移作用下坑内桩基的受力特性,重点分析了基坑开挖深度、支护结构与坑内桩基的距离、桩顶竖向荷载以及承台约束高度等对桩基弯矩和剪力的影响。
上述研究分析了基坑中桩基础的承载能力和变形特性以及既有基坑二次开挖时双层支护排桩与既有受荷桩的承载特性,而对地下空间二次开挖时双层排桩支护体系与受荷基桩共同工作特性的研究较少。为探究既有-新增双层支护桩与受荷基桩在不同基坑开挖深度下的受力特性,建立室内试验模型,以分析基坑内支护桩和基桩的桩顶位移与桩身弯矩的变化规律。
1 工程背景
某建筑平面呈近似正方形,长和宽均为33 m,占地面积为1 089 m2,主体为框架剪力墙结构,每层楼单位荷载为18.96 kPa,各楼层自重一致。该建筑只有一层地下室,原基坑开挖深度为5 m,采用直径为0.8 m的钻孔灌注桩支护,桩长为15 m,桩间距为1.5 m。拟向下增层开挖,新建一层地下车库。由于增建的地下二层车库的层高较高,新增开挖深度为13 m,需在地下室周边增设排桩支护结构。新增支护桩为直径0.8 m的钻孔灌注桩,桩长25 m,桩间距1.5 m,既有排桩支护结构与新增排桩支护结构的间距为3 m。基坑内的桩基础为钻孔灌注桩,桩径为0.8 m,桩长为37.5 m,桩间距为6.6 m,呈正方形布置,共16根,桩基础混凝土的强度等级为C30,与既有支护桩的最小间距为6.6 m。
2 试验方案
2.1 模型设计
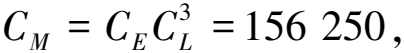

图1 模型平面示意图

图2 过模型中心线剖面图Fig. 2 Section through the model centerline

图3 模型桩示意图Fig. 3 Diagram of model pile
2.2 面积置换
由于基桩的布桩密度较高,引入置换率的概念进行简化计算,采用大面积规则布桩中的正方形布桩形式进行置换。根据置换率的定义,按照有限范围内所有桩的面积除以有限范围的总面积即可得到置换率[12]。
m=n·Ap/A=16π×0.0162/1.322=0.007 4。
(1)
其中:m为面积置换率;n为基桩的数量;Ap为单根桩的截面积,m2;A为有限范围的总面积,m2。
按正方形布桩划分单元体,单元体面积内桩的截面积为半个桩面积,此时面积置换率
(2)
其中:d为置换后的基桩直径,m;s为置换后的基桩桩间距,m。根据置换率相等,有
(3)
d/s=0.096 97。
(4)
据试验要求,基桩模型桩外径为0.05 m,厚度为0.002 m,则基桩的桩间距为0.516 m。
2.3 试验工况
室内模型试验共分9次开挖,试验参数设定及开挖深度如表1所示。

表1 实验开挖各桩及深度信息
2.4 试验步骤
1) 模拟既有工程阶段。经过测量放线,确定基桩位置,将基桩垂直放置于基坑内并进行填土,当坑内土体距离基坑顶部65 cm时,埋入既有支护桩,继续填土至距桩顶5 cm位置处,静置24 h。
2) 新增支护桩阶段。将基坑向下开挖20 cm,即原有一层地下室的几何相似高度,静置24 h,打入新增支护桩。
3) 监测仪器放置阶段。采用百分表测试新增支护桩的桩顶水平位移时,将测量杆与新增支护桩抵触,使测量杆有一定的压缩量,记录初始数值。百分表安装完成后接入高速静态应变仪,应变片采用半桥连接,实时记录桩身应变数据。
4) 开挖阶段。采用分层开挖,开挖深度为10~20 cm时,每10 cm开挖一步;开挖深度为20~30 cm时,每5 cm开挖一步;开挖至30 cm后再开挖2 cm,然后继续向下开挖3 cm,此时开挖深度达到35 cm。在开挖深度为35~50 cm时,每5 cm开挖一步,即总开挖深度为50 cm。每一步开挖完成,待土体稳定后检测桩身应变值、桩顶水平位移。
3 桩身位移及弯矩分析
由于桩呈正方形布置,四边受力及变形相同,故取基坑一边中点位置的支护桩(既有支护桩Y1、新增支护桩Y7)和基桩YT2为研究对象,如图4所示,研究支护桩及受荷基桩的相互作用。
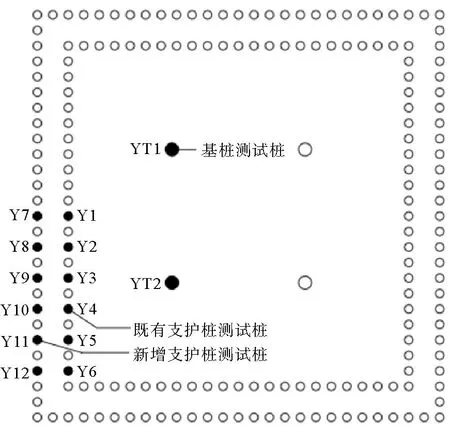
图4 测试桩编号平面图Fig. 4 Test pile number plan
3.1 桩顶位移分析
增层开挖时既有支护桩Y1与新增支护桩Y7以及基桩YT2的桩顶水平位移如图5所示。从图5可以看出,支护桩的桩顶水平位移与二次开挖深度呈正比,随着开挖深度的增加,桩顶水平位移的增长幅度越大;基桩的桩顶水平位移变化幅度很小。另外,既有支护桩和新增支护桩的桩顶水平位移都随二次开挖深度的增加而增大,但新增支护桩的桩顶水平位移增长趋势没有既有支护桩明显;在同一开挖深度时,既有支护桩的桩顶水平位移要大于新增支护桩,说明在二次开挖时,水平位移主要发生在既有支护桩上。因此,当开挖到一定深度时,既有支护桩可能会先产生倾覆破坏。随着增层开挖深度的增大,基桩的桩顶水平位移增长幅度不大,其主要原因是基桩的嵌固深度较深,说明基桩在开挖过程中一般不会发生倾覆破坏。
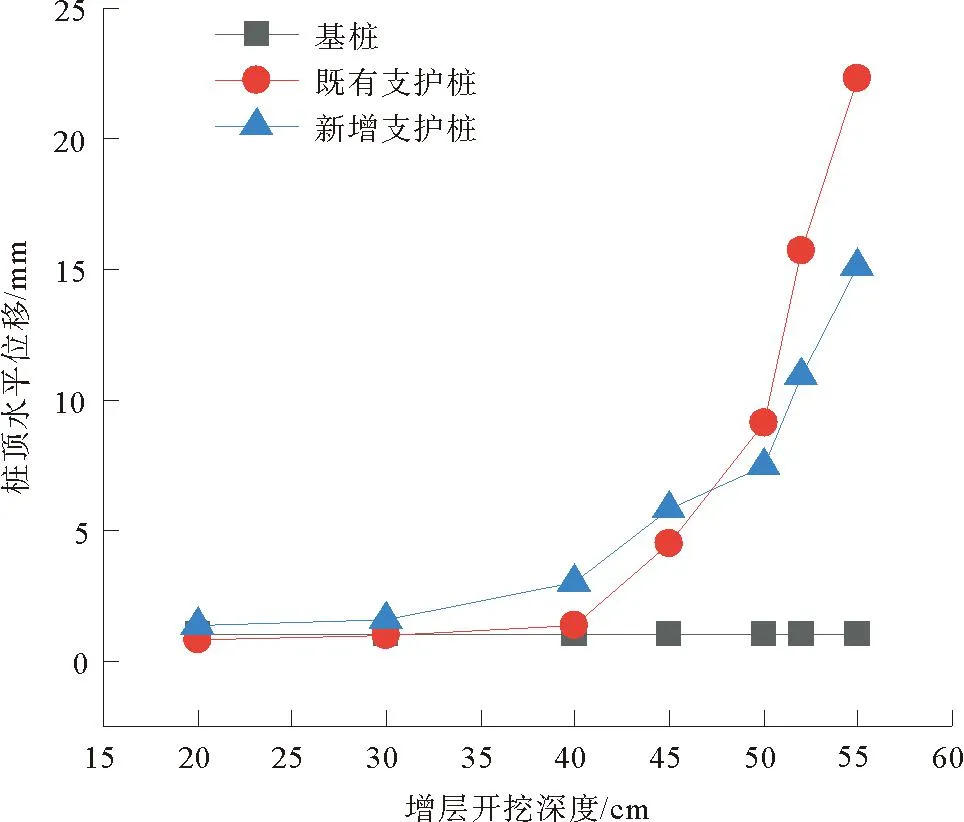
图5 桩顶位移图
3.2 桩身弯矩分析
Y1、Y7及YT2的桩身弯矩分布曲线分别如图6和图7所示。由图6(a)可知,埋深5~15 cm时既有支护桩的桩身弯矩基本不变,最大弯矩位于埋深25 cm处,最大弯矩值为168.43 N·cm。随着开挖深度的增大,弯矩逐渐减小,说明在既有支护桩外围补入新增支护桩能够分担一大部分由于开挖产生的侧向土压力,减少既有支护桩的受力。因此,从桩身弯矩方面分析,新增支护桩能够有效承担土压力,具有一定的支护能力。由图6(b)可知,新增支护桩的桩身弯矩在开挖深度H=25 cm和H=40 cm时突增;另外,新增支护桩的最大弯矩值均在埋深60 cm处,即既有支护桩失效处,说明既有支护桩倾覆后,桩间土对新增支护桩的弹性支撑作用减弱。

图6 支护桩弯矩图

图7 基桩弯矩图
如图6所示,开挖深度H为10 cm时,既有支护桩的最大弯矩值为96.60 N·cm,H分别为20、25、30、32、35、40 cm时,既有支护桩的最大弯矩值分别为168.43、160.45、134.87、120.27、120.27、107.39 N·cm;H为10、20 cm时,新增支护桩的最大弯矩值分别为12.85、39.86 N·cm;H分别为25、30、32、35、40 cm时,新增支护桩的最大弯矩值分别为131.45、175.74、182.63、175.74、198.43 N·cm。可见,在开挖10 cm之后,既有支护桩的弯矩开始急剧增长,而在开挖20 cm后,新增支护桩的弯矩才开始急剧增长,并且随着开挖深度的增加,新增支护桩的桩身弯矩要大于既有支护桩。说明既有基坑二次开挖时,中心位置处的新增支护桩能够有效承担侧向土压力和桩间土的剪应力,分担土压力的作用较强。从图7可以看出,基桩的桩身弯矩变化大致呈“S”形,弯矩最小值位于埋深65 cm处,即既有支护桩失效处,说明在既有支护桩失效前,基桩几乎不承担侧向土压力。随着开挖深度的增大,基桩的桩身弯矩呈负增长趋势,此时新增支护桩承担大部分土压力,因此新增支护桩起到至关重要的作用。既有支护桩倾覆破坏后,基桩和新增支护桩共同作用,此时基桩的弯矩开始增长。基桩弯矩的最大值位于埋深105 cm处,即新增支护桩失效处,此时既有-新增支护体系失去作用。
4 空间效应分析
二次开挖时,由于空间效应的影响,试验中同一开挖深度下,沿基坑一边分布的支护桩的工作特性会有明显差别。沿基坑的宽度方向上,桩体的最大水平变形、弯矩峰值的大小随距坑角的距离增大而增大[13]。取中心桩(Y1、Y7)、边桩(Y3、Y9)、角桩(Y5、Y11)为研究对象,分析在空间效应作用下不同位置的支护桩承载特性的变化规律。在室内模型试验中,基坑平面为边长132 cm的正方形,中心桩位于基坑边中点,边桩距中心桩24 cm,角桩距中心桩48 cm。
不同位置支护桩的桩顶水平位移变化规律如图8所示。由图8(a)可知,既有支护桩的桩顶水平位移增速随二次开挖深度的增加而逐渐增大,且中心桩的桩顶水平位移增长速度最快,角桩的增长速度最慢,边桩位于中心桩和角桩之间。由图8(b)可知,同一开挖深度下,新增支护桩的桩顶水平位移变化规律与既有支护桩相同。与既有支护桩不同的是,随着二次开挖深度的增加,新增支护桩的桩顶水平位移增长速率没有明显提升。从中心桩到边角桩,既有支护桩和新增支护桩的桩顶水平位移都呈减少的趋势,说明基坑两侧壁土体具有一定的限制作用,使支护桩在二次开挖作用下产生的桩顶水平位移呈现中间大、两边小的趋势,且空间效应对既有支护桩的影响较大,对新增支护桩的影响较小。
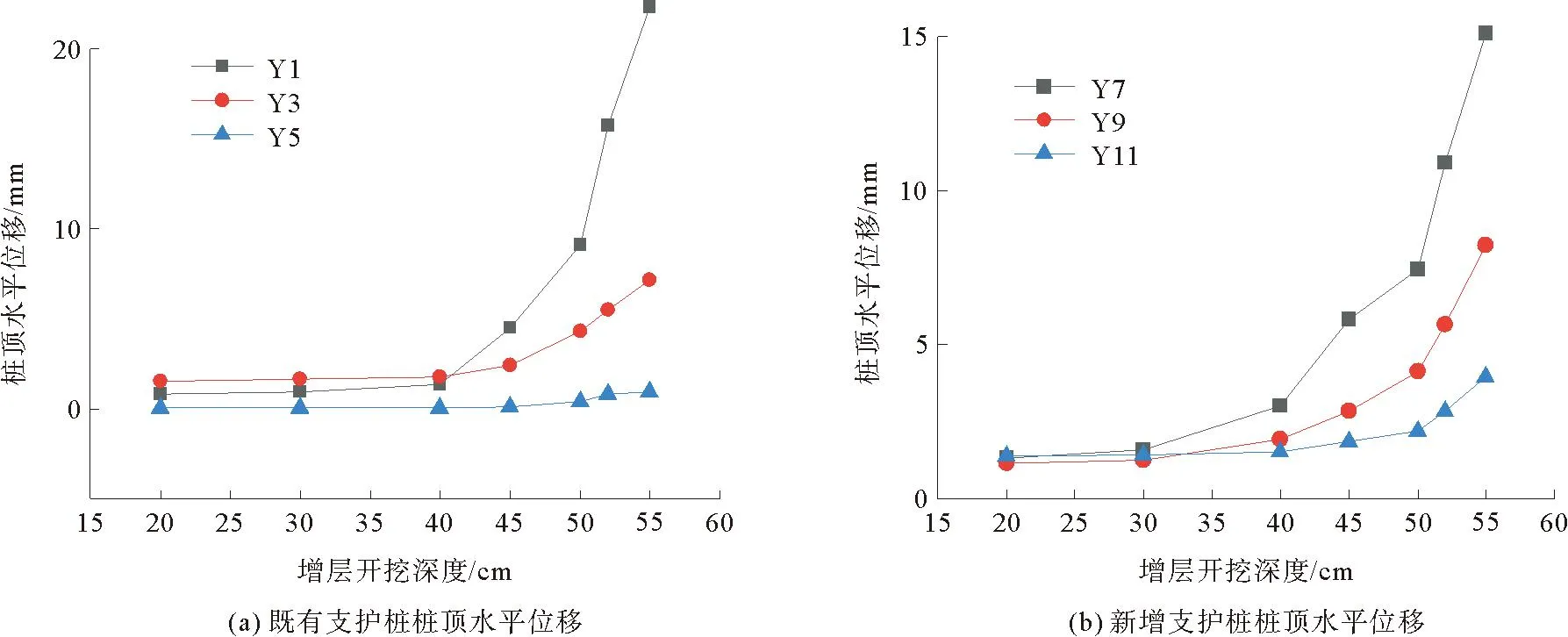
图8 不同位置处支护桩桩顶水平位移
模型试验得到不同位置既有支护桩和新增支护桩的桩身弯矩分布规律,如图9和图10所示。由图9可知,在同一开挖深度,不同位置既有支护桩的桩身弯矩大小不同,表现为中心桩的桩身弯矩最大,边桩其次,角桩的桩身弯矩最小,虽然不同位置既有支护桩的桩身弯矩相差不大,但其桩身弯矩的分布规律较为相似,都呈中间大、两边小的趋势[14]。由图10可以看出,不同位置新增支护桩的桩身弯矩分布类似于既有支护桩,但中心桩与角桩的最大桩身弯矩相差较大。不同位置支护桩的桩身弯矩不同主要是受到空间效应的影响,支护桩在同一基坑边受到的侧向土压力不同,土压力沿基坑边方向呈抛物线分布,因此中心桩受力最大,角桩受力最小,边桩介于两者之间。从支护桩受力角度分析,中间区域为支护桩受力的薄弱区域[15],可推断出开挖到一定深度时中心桩可能最先倒塌破坏,而边角桩的支护效果较好。总体上,在中心位置处新增支护桩的桩身弯矩大于既有支护桩,而在边角位置处弯矩值比既有支护桩小,说明新增支护桩为主要的受力支护体系,在中心位置处分担土压力的作用更强,在边角位置处分担土压力的能力较弱。
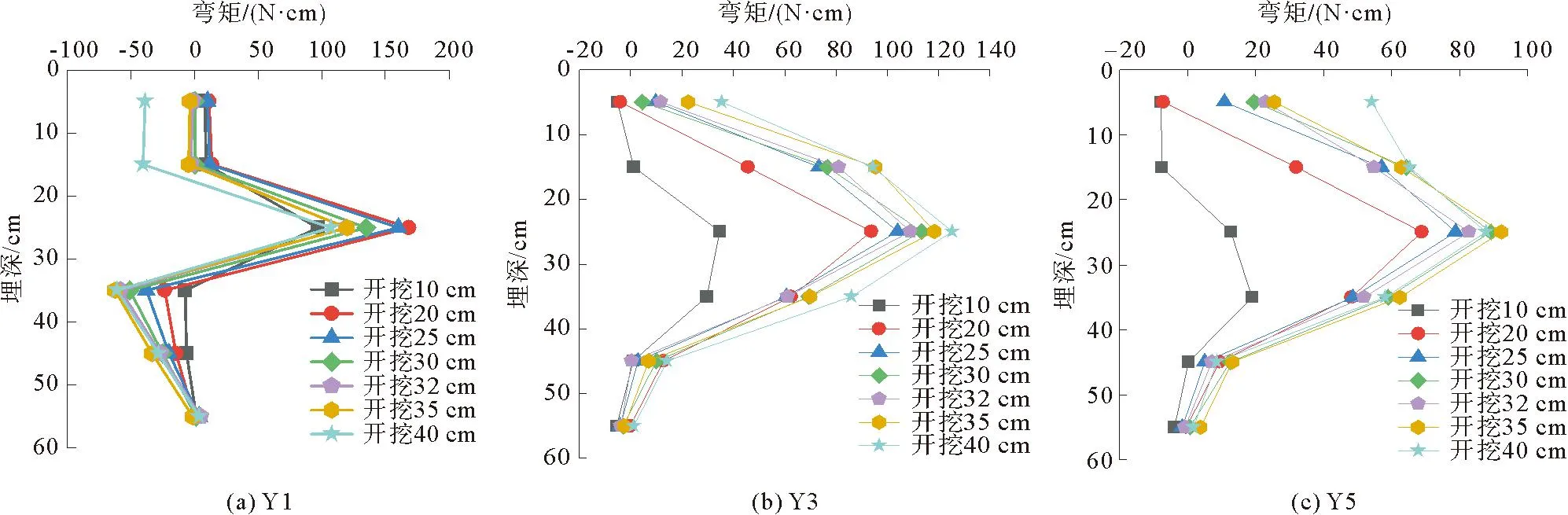
图9 不同位置处既有支护桩桩身弯矩
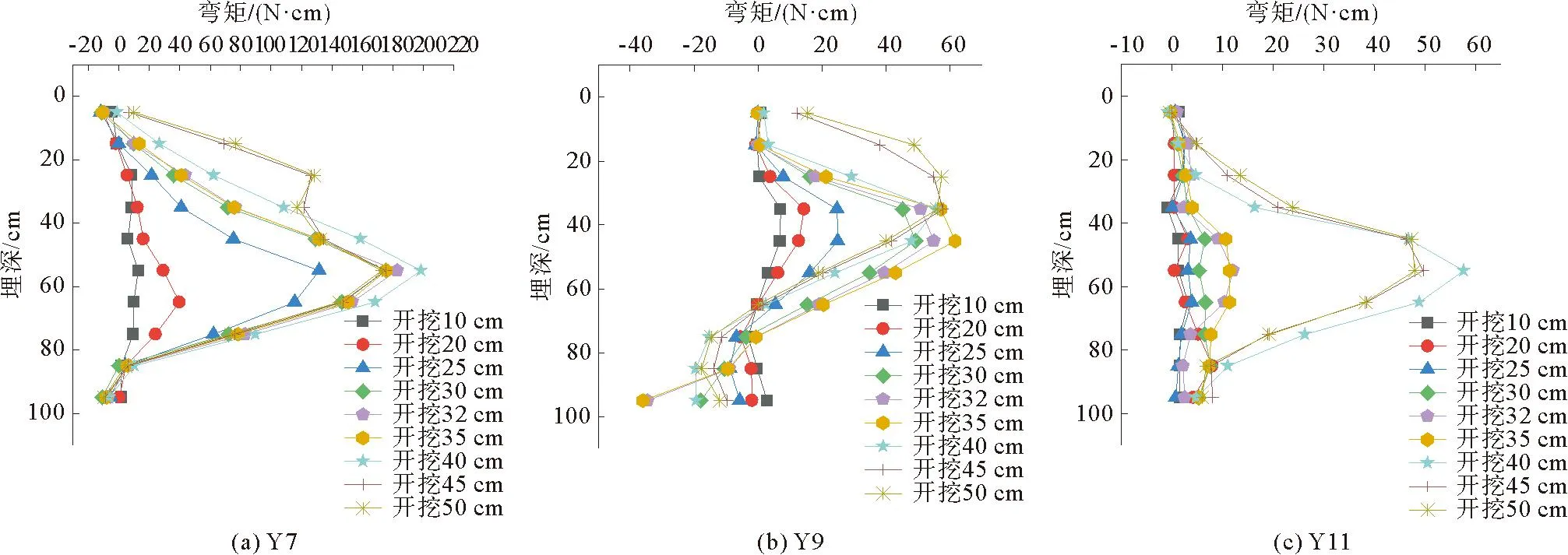
图10 不同位置处新增支护桩桩身弯矩
5 结论
1) 在中心位置,随着开挖深度的增加,既有、新增支护桩的桩顶水平位移不断增大。开挖深度40 cm以内,桩顶水平位移增长缓慢,开挖深度超过40 cm,支护桩桩顶位移急剧增长,但新增支护桩的桩顶水平位移增长速度比既有支护桩缓慢,基桩的桩顶水平位移随开挖深度增加变化不大。
2) 在中心位置,开挖深度较小时,既有支护桩和新增支护桩桩身弯矩相差不大,但随着开挖深度的增加,新增支护桩的桩身弯矩要远大于既有支护桩,且在开挖10 cm后,既有支护桩桩身弯矩急剧增长,而新增支护桩在开挖20 cm后,桩身弯矩随开挖深度急剧增长。基桩桩身弯矩呈“S”型分布,在既有支护桩退出工作前,桩身弯矩呈负向缓慢增长,而在既有支护桩失效后,桩身弯矩呈正向且迅速增长,桩身最大弯矩出现在新增支护桩失效时。
3) 受空间效应的影响,从中心桩到边角桩位置,支护体系的桩顶水平位移逐渐减小,但既有支护桩的减小趋势要远大于新增支护桩。随着二次开挖深度的增大,中心桩的桩顶位移增长速度最快,角桩的增长速度最慢,边桩位于中心桩和角桩之间。
4) 既有基坑二次开挖条件下,支护桩的桩身弯矩呈中间大、两边小的趋势。既有支护桩和新增支护桩的桩身最大弯矩值都呈线性增长;受到空间效应的影响,中心桩的桩身弯矩最大,其次是边桩,角桩最小,在中心位置处新增支护桩的桩身弯矩大于既有支护桩,而在边角位置处小于既有支护桩。

