基于张量环分解的三维地震数据重建方法

张杏莉,刘作刚,张亚萍,赵卫东

(山东科技大学 计算机科学与工程学院,山东 青岛 266590)

地震数据采集受采集环境和地理条件的限制,容易造成数据不完整,低质量的地震数据对后续地震数据处理和解释工作产生较大影响,因此地震数据重建已成为地震数据处理的重点研究内容之一。数据重建是在数据缺失的情况下,利用少量的数据预测、补全缺失的数据。目前常用的数据重建方法有滤波器、函数变换、压缩感知和降秩等。

基于滤波器的方法通过缺失数据与某种插值滤波器的卷积来获得重建数据。Spitz[1]提出f-x域插值重建方法,在f-x域中使用低频数据重建高频数据;Naghizadeh等[2]提出线性预测滤波器重建方法,在规则的网格下重建不规则的数据。但基于滤波器的方法只能处理规则的数据。基于函数变换的方法先对地震数据进行正变换编码,然后在变换域内插值,再进行反变换解码,进而对数据重建。Jahanjoo等[3]提出抗泄漏傅里叶变换方法,通过正则化处理不规则的数据,但是当输入的数据比较混叠时数据重建效果不理想,并且傅里叶变换是一种全局变换,不能准确地表示局部特征;唐欢欢等[4]提出3D高阶抛物Radon变换方法,解决了3D不规则数据的重建问题,但Radon变换处理复杂曲线事件的能力较差;Zhang等[5]通过多尺度、多方向的Curvelet变换对较大规模的数据进行处理;文献[6]采用一种非等间距的离散Curvelet变换方法对非均匀采样的数据进行处理;张凯等[7]将Shearlet变换和离散余弦变换字典相结合进行数据重建。但是函数变换方法的基函数是固定的,不能根据地震数据的特征自适应地选择基函数[8]。压缩感知理论是一种新的信号处理方法,可以由远少于采样定理要求的采样点重建恢复,目前已经被应用到地震数据重建中。Zhang等[9]提出基于随机样本的压缩感知方法,通过将样本划分为若干子集以获得重建结果;孙苗苗等[10]将形态成分分析与压缩感知结合,消除了空间假频;段中钰等[11]将压缩感知和平方正则交替方向乘子法结合,消除了过拟合现象。但压缩感知方法难以满足地震道大范围缺失的情况。降秩是地震数据重建的另一种方法,如低秩矩阵补全方法[12]、基于奇异值分解(singular value decomposition, SVD)的低秩约束和曲线域稀疏约束的重建方法[13-14],而在低秩矩阵上进行核范数约束的方法变得越来越广泛。Wang等[15]提出加权核范数最小化方法,通过迭代重新加权使加权核函数模型接近于“计数秩函数”并且可以提升低秩矩阵,但核范数最小化是指所有奇异值之和的最小化,不等于核函数的最小值;Zhang等[16]对核范数正则化,从而对更少的奇异值最小化,可以更加逼近秩函数,但是奇异值分解会消耗大量的计算资源;多通道奇异谱分析方法是一种数据驱动方法,该方法基于Hankel矩阵的截断奇异值分解,通过频率切片进行数据重建[17]。但是传统的低秩或降秩矩阵补全方法在三维数据的应用中仍存在一些重建误差。

张量环(tensor ring, TR)分解是一种新的数据补全方法,对数据特征没有要求,可以处理复杂的事件,并且可以有效利用三维数据的结构信息,被广泛应用于图像的缺失数据重建,如子空间非局部张量环分解的高光谱图像重建[18]、全变分正则化张量环分解的遥感图像重建[19]、张量环低秩因子(tensor ring low-rank factors, TRLRF)缺失图像重建[20]等。本研究将TRLRF方法首次应用于地震数据重建,先通过张量环分解将三维地震数据转换为小的三维数据的乘积,再利用交替方向乘子法(alternating direction method of multipliers, ADMM)和增广拉格朗日函数对小的三维数据求解,最后通过循环多线性乘积将小的三维数据恢复为大的三维数据,实现对三维地震数据的重建。仿真数据和真实数据实验结果均表明,TRLRF方法在重建效率和重建质量上都有较大优势,重建效果良好。

1 方法原理

1.1 张量环分解

本研究采用Kolda等[21]和Long等[22]所提出的符号和定义。张量环分解是通过一系列低维核张量上的循环多线性乘积表示大维张量,这一系列低维核张量称为TR因子。对于n=1,2,…,N,TR因子可以用C(n)∈RRn×In×Rn+1表示,其中Rn(1≤n≤N)表示TR的秩,R1=Rn+1,In是原始张量的维度。对于一个

N阶张量A∈RI1×I2×…×IN,张量环分解的定义为:

(1)

图1 张量环分解

1.2 张量环低秩因子

将ADMM和增广的拉格朗日方程相结合,TRLRF方法的表达式为[20]:

(2)

C(n)、W(n,i)和U(n,i)都是相对独立的,式(2)可以通过以下过程更新。

1) 更新C(n)。

(3)

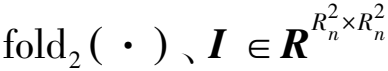
2) 更新W(n,i)。

(4)

3) 更新U(n,i)。

U(n,i)=U(n,i)+η(W(n,i)-C(n))。

(5)

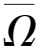
4) 更新A。A通常在相应的数据中输入观测值更新,并且在每次迭代中通过TR因子[C]近似缺失的数据,即:

(6)

2 TRLRF方法的影响因素及复杂度分析

2.1 秩的选择

在张量环分解中一个关键问题是如何选取最优秩。一个地震数据体包含的地震信息都是相互关联的,秩选取过小会导致TR因子中的数据信息过少,秩选取过大会导致TR因子中存在过多的干扰数据。因此,秩选取过大或过小均会使TR因子不能准确地近似缺失的数据,导致重建效果差。同时,秩选取过大会增加方法运行时间,影响重建效率。本研究通过对秩取不同值时的信噪比(signal-to-noise ratio, SNR)、均方根误差(root mean square error, RMSE)以及运行时间等评价指标进行统计分析确定最优秩的值。

分别使用两个包含线性事件(数据1、数据2)、两个包含曲线事件(数据3、数据4)的仿真数据对秩的选择进行实验,并计算重建后数据的SNR、RMSE和运行时间,实验结果如图2所示。由图2(a)可知,随着秩的增加,重建后的仿真数据的SNR值逐步升高,当秩为10时SNR值取得最大值,当秩大于10时SNR值趋于稳定或稍有下降趋势;由图2(b)可知,随着秩的增加,RMSE值逐渐降低,当秩为10时RMSE取得最小值,当秩大于10时RMSE趋于平稳或逐渐增加。可见,秩为10时4个仿真数据的重建效果最好。由图2(c)可知,随着秩的增加,TRLRF方法所需运行时间快速增加。因此,综合考虑重建后数据的SNR、RMSE以及重建所需的运行时间,认为秩的值取10时可以获得最好的重建结果并且保持良好的重建效率。因此,TRLRF方法中秩的值选择为10。

图2 不同秩时的SNR、RMSE和运行时间

2.2 TRLRF方法及复杂度分析

表1 不同重建方法的时间复杂度

方法 1. 基于张量环分解的地震数据重建方法 1) Input:missing seismic data PΩ(T), TR-rank{Rn } N n= 1 = 10 2) Initialization:For n = 1,…,N,i = 1,2,3, random sample C (n) by N ～ (0,1),ξ = 10,η = 0. 9,tol = 10 -8 ,kmax = 500,W (n,i) = 0,U (n,i) = 0. 3) For k = 1 to kmax do 4) Apre = A . 5) Calculate (C (≠n),T (2) C (≠n) (2) ) -1 ,A < n > C (≠n) (2) . 6) Update {C (n) } N n = 1 by (3). 7) Calculate S 1 η C (n) (i) - 1 η U (n,i) (i) ) . 8) Update {W (n,i) } N,3 n = 1,i = 1 by (4). 9) Update {U (n,i) } N,3 n = 1,i = 1 by (5). 10) Update A by (6). 11) If mse(A - Apre) < tol ,break. 12) End for 13) Output:reconstructed seismic data

由表1可见,尽管OMPHR方法中K的阶次比较低,但时间复杂度中含有数据维度平方相乘项,DDTF方法也包含维度平方相乘项,而TRLRF方法复杂度仅为维度平方之和,所以数据量较大时,TRLRF方法的时间复杂度比DDTF和OMPHR方法低。

3 实验分析

为验证TRLRF方法的有效性,分别对仿真数据的地震道随机缺失和实际三维地震数据(来源https:∥wiki.seg.org/wiki/Kerry-3D)的地震道随机缺失、规则缺失进行实验。

在地震数据重建方法中,把数据划分为字典小块的字典学习和对数据的每个二维频率切片的矩阵补全的重建方法都是典型方法。近年来,有学者将深度学习应用于地震数据重建,但是需要大量样本数据进行训练和测试。故本研究选用基于字典学习的DDTF方法和基于矩阵补全的OMPHR方法作为本研究的对比方法。

3.1 实验结果评价指标

本研究采用地震数据重建后的SNR、RMSE和运行时间3个指标验证数据重建的效果和效率。SNR(SNR)和RMSE(RMSE)两种指标分别定义为:

(7)

(8)

式中:f是完整原始地震数据,f0是重建地震数据,mean(·)表示元素的平均值。信噪比越高表明重建数据越接近原始数据,均方根误差是重建后的地震数据偏离原始数据平均值的度量,均方根误差越小表示重建的数据越接近原始数据。

3.2 仿真数据实验及分析

为验证TRLRF方法的有效性和优越性,使用Marmousi2构造仿真地震数据,图3(a)为原始仿真数据的正面切片,图3(b)为随机缺失50%的仿真数据。从图3(b)可以看出,在缺失50%的数据后,该地震数据损坏严重。分别使用TRLRF、DDTF和OMPHR方法对图3(b)所示地震数据进行重建,重建后的地震数据如图4所示。

图3 原始仿真数据与地震道随机缺失50%的仿真数据

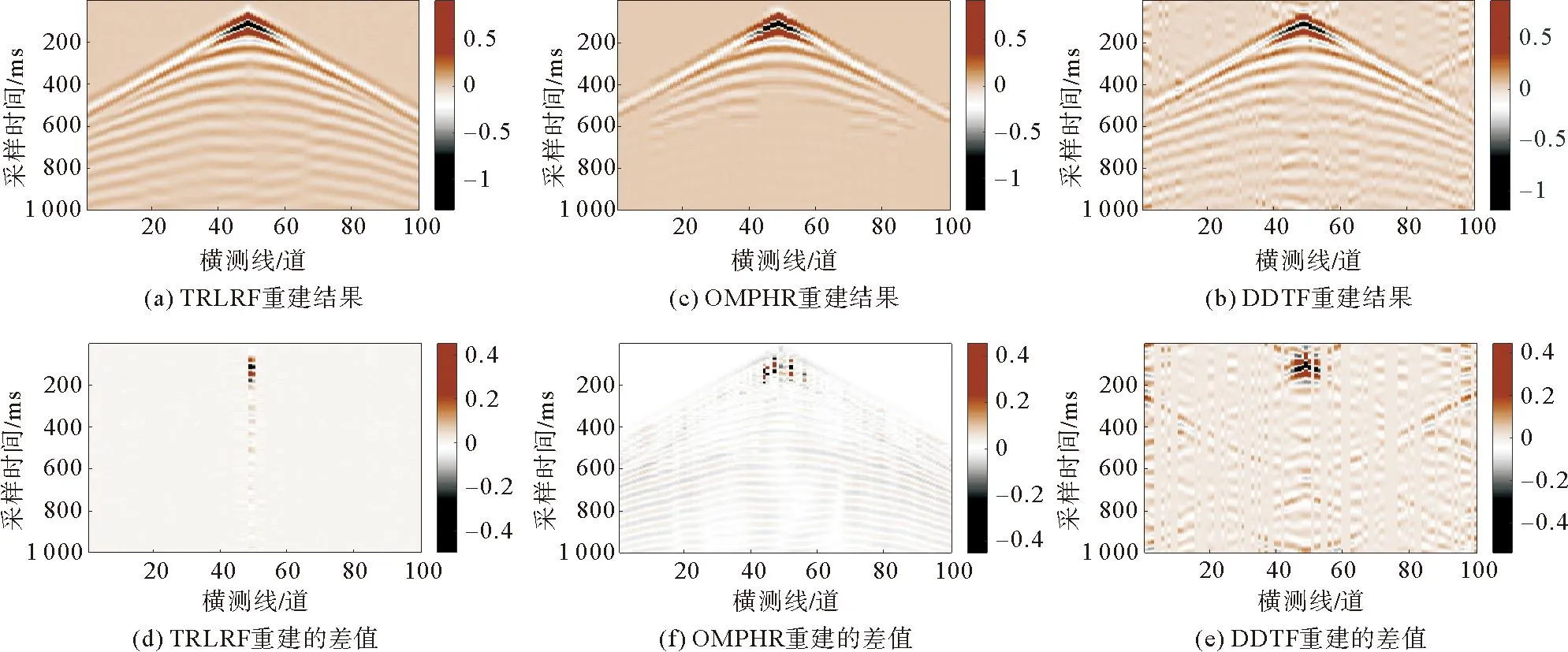
图4 地震道随机缺失50%的仿真数据的正切面重建结果

由图4可知,原始仿真数据在采样点600之前地震波的幅值较大,特征比较明显,而在采样点600之后地震波的幅值较小,波形趋于平缓。DDTF方法在重建过程中通过小块数据形成训练集恢复缺失的数据,在幅值较小、特征不明显的情况下恢复数据能力较差,故DDTF方法在采样点600之后的重建效果较差。OMPHR方法通过二维切面的频率切面和对每个切面进行反平均生成每一列以恢复缺失的数据,在进行反平均生成每一列时容易造成数据的混乱,因此,OMPHR方法在重建后产生反向波的混乱现象。而TRLRF方法通过张量环分解有效利用了三维数据的结构信息,能保证划分的块包含更多的特征,使用适合解决结构复杂问题的交替方向乘子法求解划分的块,从而获得更好的重建结果。

从微观角度进一步对比3种方法的重建效果,对第65条缺失的单个信道的原始数据与重建结果进行对比,如图5所示。由图5可看出,TRLRF方法较完整地重建了缺失的数据,而DDTF方法对采样点520后幅值较小的波形重建效果差,OMPHR方法在采样点500后有明显振荡,重建质量较差。

图5 不同方法重建后的第65条信道

为了验证不同缺失率下3种方法的重建效果,对3种方法的SNR进行分析,结果如图6所示。由图6可以看出,TRLRF方法在不同缺失率下的重建质量均优于DDTF和OMPHR方法。

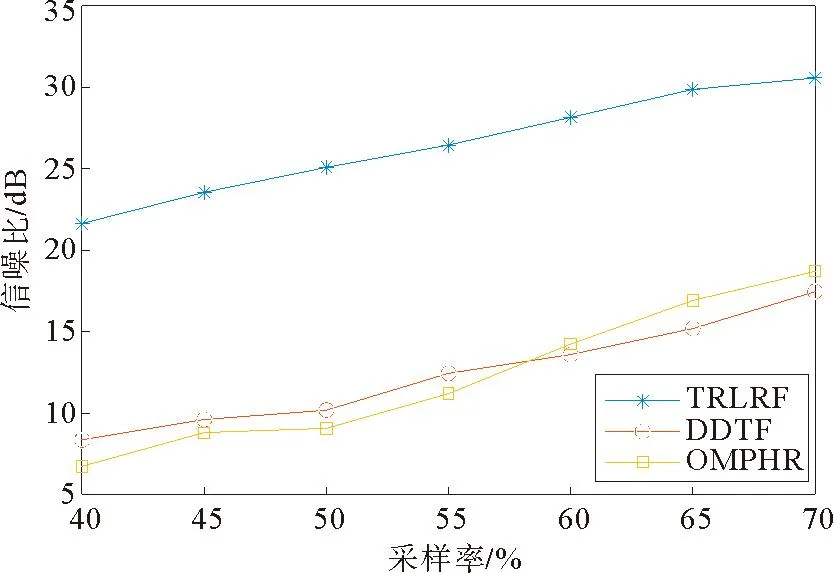
图6 仿真数据的不同采样率与信噪比的关系

分别计算TRLRF、DDTF和OMPHR方法在地震道随机缺失50%重建后的SNR、RMSE和运行时间,计算结果见表2。分析表2可知,TRLRF方法在缺失率相等的条件下取得最高的SNR和最低的RMSE。由此可以看出,TRLRF方法在仿真数据的重建质量上比DDTF和OMPHR方法都要优越,并且TRLRF方法的运行时间最小,具有较高的重建效率。

表2 仿真数据地震道随机缺失时重建结果对比

3.3 真实数据实验及分析

使用真实地震数据(来源https:∥wiki.seg.org/wiki/Kerry-3D)进行实验,如图7、图8所示。

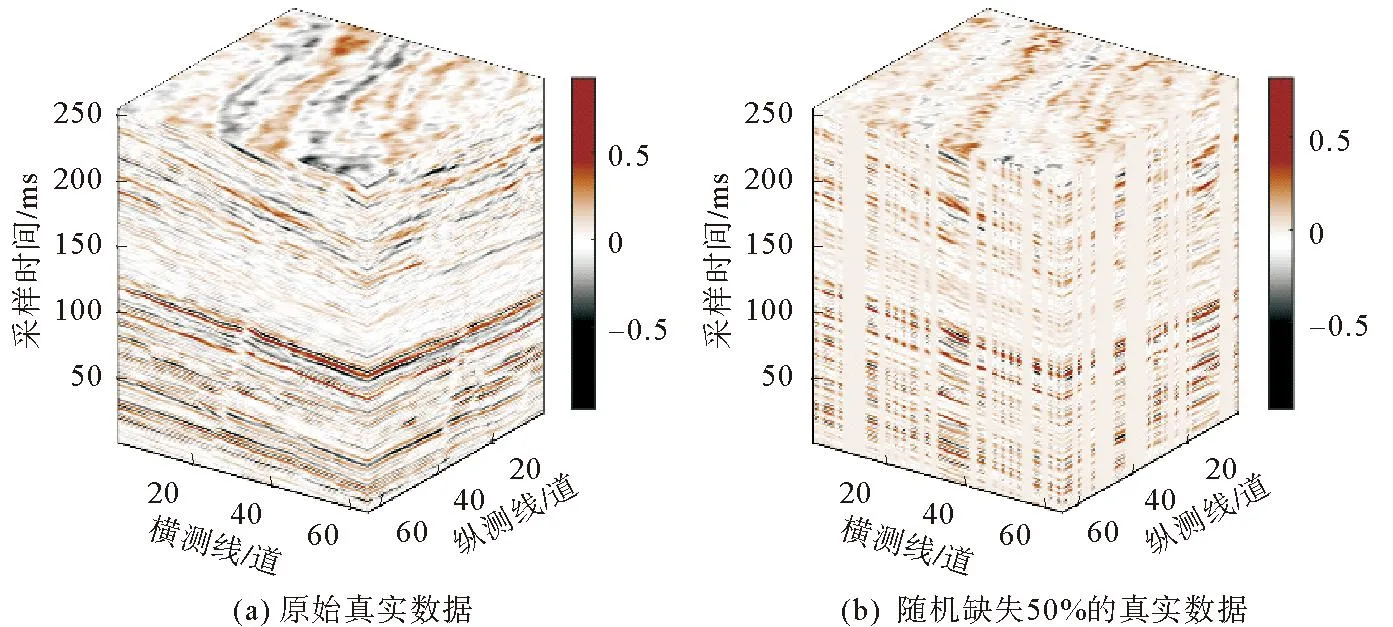
图7 原始三维真实数据与地震道随机缺失50%的三维真实数据

图8 原始三维真实数据与地震道随机缺失50%的三维数据的各切面示例

分别使用TRLRF、DDTF和OMPHR方法对图7(b)缺失的数据进行重建,其正切面的重建结果如图9所示。由图9可以看出,DDTF方法重建的数据存在大面积误差,重建效果差;OMPHR方法重建的数据在某些地震道上存在误差,重建效果较差;而TRLRF方法在整体重建质量上优于DDTF和OMPHR方法。这是由于DDTF方法是把数据划分为小块数据形成训练集,通过训练集对缺失的数据进行估计,训练过程中对特征不明显的数据不敏感,不能较好地补全缺失的数据。OMPHR方法是把三维数据的每个二维切面转换为频率切面,对每个切面采用OR1MP方法将矩阵表示为秩为1的基矩阵的线性组合,但是对于秩比较大的缺失数据来说,秩为1的基矩阵的线性组合不能很好地表示原始数据,从而不能很好地恢复缺失的数据。而TRLRF方法通过张量环分解有效利用了三维数据的结构信息,保证划分的块包含更多地特征,使用适合解决结构复杂问题的交替方向乘子法求解划分的块,从而获得更好的重建结果。

图9 地震道随机缺失50%的三维真实数据的正切面重建结果

从微观角度进一步对比3种方法的重建效果,对正切面的第33条缺失的单个信道的原始数据与重建结果进行对比,如图10所示。从图10可以看出,TRLRF方法较完整的重建了缺失的数据,而DDTF和OMPHR方法存在振荡,重建质量较差。

图10 不同方法重建后正切面的第33条信道

为了说明3种方法在不同缺失率下的良好重建性能,对3种方法在不同缺失率下重建后的SNR进行分析,如图11所示。由图11可以看出,TRLRF方法在不同缺失率下的重建质量均优于DDTF和OMPHR方法。

图11 真实数据的不同采样率与信噪比的关系

分别计算TRLRF、DDTF和OMPHR方法在地震道随机缺失50%重建后的SNR、RMSE和运行时间,计算结果见表3。分析表3可知,TRLRF方法的SNR最高,而OMPHR方法重建的SNR仅为TRLRF方法的1/2;TRLRF方法的RMSE值最小,可见,TRLRF方法重建后的三维地震数据最接近原始三维地震数据;同时,TRLRF方法的运行时间相对于DDTF和OMPHR方法最短。因此,TRLRF方法具有良好的重建效率。

表3 真实数据地震道随机缺失时重建结果对比

表4分别给出了真实数据地震道随机缺失时上切面、侧切面和正切面的SNR和RMSE结果。从表4可知,TRLRF方法在各个切面的重建效果优于DDTF和OMPHR方法。

表4 真实数据地震道随机缺失时各切面重建结果对比

对地震数据的规则缺失进行实验,进一步说明TRLRF方法能够很好地重建缺失数据,如图12、图13所示。分别使用TRLRF、DDTF和OMPHR方法对图12缺失的数据进行重建,其侧切面的重建结果如图14所示。由图14可以看出,DDTF方法重建的数据存在大面积误差,重建效果差;OMPHR方法重建的数据在某些地震道上存在误差,重建效果较差;而TRLRF方法在整体重建质量上优于DDTF和OMPHR方法。这是由于DDTF方法是把数据划分为小块数据形成训练集,通过训练集对缺失的数据进行估计,在训练过程中对特征不明显的数据不敏感,不能较好地补全缺失的数据。OMPHR方法是把三维数据的每个二维切面转换为频率切面,难以充分利用三维数据的结构信息,不能很好地恢复缺失的数据。而TRLRF方法通过张量环分解有效利用了三维数据的结构信息,可保证划分的块包含更多特征,使用适合解决结构复杂问题的交替方向乘子法求解划分的块,从而获得更好的重建结果。

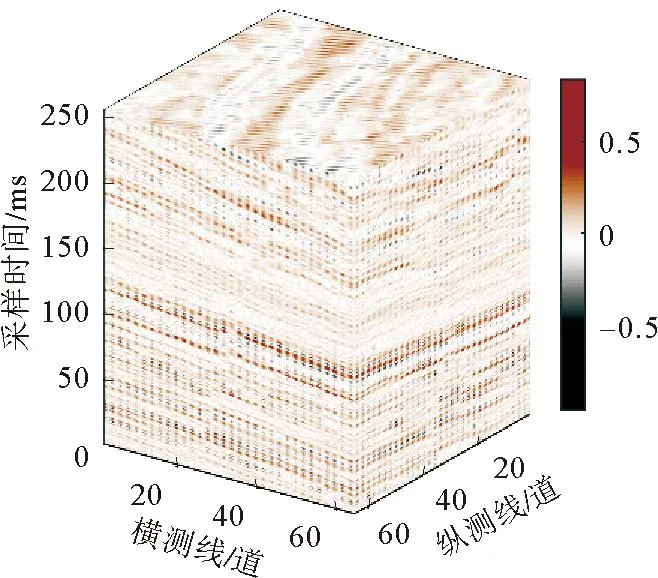
图12 地震道规则缺失50%的三维真实数据

图13 地震道规则缺失50%的三维真实数据的各切面示例

图14 地震道规则缺失50%的三维真实数据的侧切面重建结果

分别计算TRLRF、DDTF和OMPHR方法在地震道规则缺失50%重建后的SNR、RMSE和运行时间,结果见表5。分析表5可知,TRLRF方法的SNR最高,是DDTF和OMPHR方法重建的SNR值的两倍多;TRLRF方法的RMSE值最小,重建后的三维地震数据更接近原始三维真实地震数据。同时,TRLRF方法的运行时间均小于DDTF和OMPHR方法。可见,TRLRF方法具有良好的重建效率。

表5 真实数据地震道规则缺失时重建结果对比

表6分别给出了真实数据地震道规则缺失时上切面、侧切面和正切面的SNR和RMSE结果,可以看出TRLRF方法在各个切面上的重建效果均优于DDTF和OMPHR方法。

表6 真实数据地震道规则缺失时各切面重建结果对比

4 结论

本研究针对三维地震数据缺失重建问题,提出一种基于隐空间上张量环低秩因子的地震数据重建方法。张量环分解方法对数据特征要求低,能够处理幅值较低、特征不明显的数据,并且能够充分利用三维数据的结构信息。仿真数据和真实地震数据的实验结果表明,在SNR、RMSE和运行时间等量化指标下,与DDTF、OMPHR方法相比,TRLRF方法重建效果较好,同时针对较大的三维地震数据,张量环分解可有效提高计算效率。本研究依据仿真三维地震数据在不同秩时的重建效果确定张量环分解中最优秩,该方法具有一定的参考意义。复杂三维地震数据在进行张量环分解时的最优秩的自适应选取是下一步的研究方向和研究重点。