煤矿工作服的上衣原型研究

刘淑强，张 洁，吴改红，高 伟，姚容程

（太原理工大学 轻纺工程学院 山西晋中 030600）

1 引言

煤矿矿井恶劣的环境对煤矿工人的工作效率、身心健康等有较大的负面影响。对煤矿工人的个体防护不仅能在一定程度上减少矿井安全问题，还可以预防职业病[1]。煤矿工作服是煤矿工人个体防护中最重要的部分，不仅可以遮身蔽体，还起到保障矿工安全和身体健康的作用[2]。由于长期劳作，煤矿工人的体型产生了一些变化，与标准体型有一定的差异，致使目前使用的矿工服存在很大的结构设计问题。解决这一问题的关键在于把握矿工体型规律，找到适合矿工体型的原型。目前专门针对煤矿工作服的原型及版型的研究很少[3]。本文研究了矿工的体型规律，通过随机抽样测量矿工的5 项身体数据，分析各项数据间的数值关系，最终以胸围为基准，建立适合矿工体型的上衣原型。

2 矿工体型测量

本次测量随机选取年龄20 ～50岁，从业一年以上的男性矿工，样本量50 人。采用马丁测量法对矿工人体进行测量，主要工具有测高仪、皮尺、直角规、弯角规、量角器等工具，对人体5 个关键项目：胸围、腰围、臂展、肩宽、身高进行测量分析。

3 体型项目回归分析

回归分析以肩宽为例，建立肩宽的回归方程。其他测量项目与肩宽回归模型的建立相同，故其他部位仅给出结果。本文采用SPSS 软件中的前进法（Forward），筛选对因变量作用大的自变量作为最终的自变量[4]。以肩宽为例，筛选自变量因变量，逐步建立肩宽的回归模型Y=aX+b。

肩宽回归模型摘要如表1 所示，复相关系数R 表明了自变量与因变量的线性回归性强弱，本项目R 值为0.956，R2为0.914，调整后的R2为0.912，估计的标准误差为0.7972，数值的大小很好地说明了肩宽与身高有较强的回归关系。

表1 模型摘要（肩宽）

表2 方差分析（肩宽）

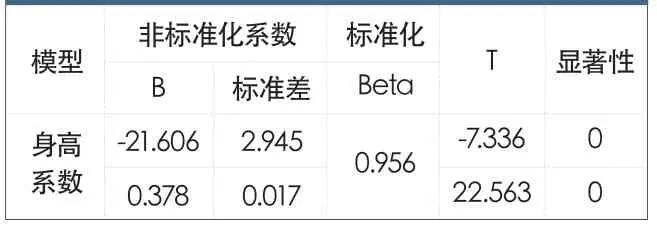
表3 回归系数分析（肩宽）

肩宽的方差分析，如表2 所示。由表中数据可知，肩宽回归方程式的平方和为323.497。F 值为509.068，代表回归模型均方与残差均方之比，该值大于95%置信区间临界值，回归系数大于0，故回归模型有效。

由表3 可知，肩宽的回归常数和偏回归系数标准差。偏回归系数真实地反映了自变量的重要性，回归模型中身高为自变量，对于肩宽来说非常重要。肩宽的T 检验值为-7.336，拒绝偏回归系数为0 的假设。

由此可得出肩宽的回归方程为：肩宽=0.378 身高-21.606

其他测量部位回归模型的建立方法与肩宽相同，其它部位依次与身高、胸围等建立回归模型如下：

胸围=10261 身高-131.656

腰围=1.174 胸围-21.441

臂长=0.945 身高-32.042

4 服装松量设置

4.1 松量概述与计算

松量大小是由服装与人体的孔隙来决定的[5]。在山西某中型煤矿对矿工进行调查后发现，一般煤矿工人在井下的着装为秋衣（厚度约0.2 cm）、秋裤（厚度约0.2 cm）、棉袄（厚度约0.8 cm）。容纳秋衣、秋裤、棉袄所需要的松量为6.3 cm 左右。

4.2 松量与皮肤变化率

一般情况下，人体的运动会导致皮肤表面横向伸长，影响服装横向方向上的最小放松量[6]。横向放松量主要包括服装围度的松量，如表4 所示。

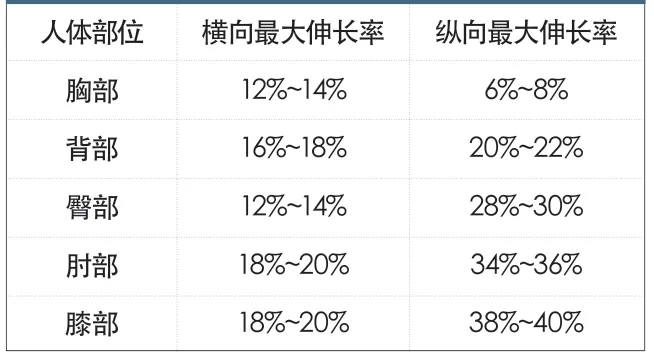
表4 人体不同部位的皮肤变化率

4.3 胸围松量

表5 人体姿势、动作与腰围放松增加量的关系

胸围松量主要考虑生理放松量和运动放松量[7]。生理放松量经过测量，成人作深吸气时，胸围的平均变化量为2.1cm；作深呼气时，胸围的平均变化量为0.8cm。再考虑皮肤弹性因素，得出胸围最小松量为4cm 左右。运动放松量的计算需要假设净胸90cm，胸、背宽34cm（宽松款式下，将胸背宽取肩宽）。根据横向最大伸长率：胸部伸长量为4.08～4.76cm，背部伸长量为5.44～6.12cm。由此可知胸围运动松量最小值为8.84～11.56 cm。两项相加，胸围放松量即为12.84～15.56 cm。

4.4 腰围松量

腰部后部运动幅度小，松量设置较小；由于人体呼吸与腰部前屈等动作，腰部前部松量明显大于后部。通过计算，腰部的基本放松量可设置在0～2 cm 内。煤矿工人在井下工作时会出现大幅度的动作，根据表5 所测量的数据，满足运动舒适量的放松量应该考虑松量最大的数值，所以运动放松量为3～4 cm。与基本放松量结合，腰部总放松量为5～6 cm。

5 矿工服上衣原型建立

现以净胸围90cm 为例，依据以上回归分析和松量计算，构建矿工服上衣原型，如图1 所示。