基于隐式参数化建模的发动机舱盖结构优化

王峻峰，印明勋，乔鑫

基于隐式参数化建模的发动机舱盖结构优化

王峻峰，印明勋，乔鑫

（华晨汽车工程研究院，辽宁 沈阳 110141）

为提升某发动机舱盖模态频率与刚度性能，建立隐式参数化模型。以结构在不同约束或加载位置下表现出不同的刚度性能为依据，研究此发动机舱盖的缓冲块在不同位置处对刚度性能的影响。将此作为设计变量，结合发动机舱盖断面尺寸，支撑梁位置设计变量进行多目标优化并研究了各变量对性能的影响。结果表明，缓冲块沿整车坐标系下的X向及Y向移动，对各项刚度性能均有不同程度的影响。同时，多目标优化对弯曲刚度及前角刚度性能有明显的提升，获得了更为合理的结构。

隐式参数化；发动机舱盖；缓冲块；多目标优化

前言

缩短开发周期，加快产品设计与验证速度对于汽车企业来说是提升竞争力的有效手段之一。传统的“CAD方案—CAE验证—方案修改—验证……”过程十分繁杂、耗时[1]。隐式参数化建模技术使得CAE分析在无CAD数据的前提下提前进入到开发早期阶段，通过建立全参数化模型，快速实现设计人员想要的设计方案并自动生成满足分析需求的网格，完成CAE分析，获得相关性能。同时，可变的参数化模型可以嵌入到优化分析流程中，实现对结构各部位尺寸，形状的最优化设计。

目前，汽车结构优化一般从零件的尺寸，形状，以及厚度等方面进行，但对于刚度非均匀分布的结构来说，其支撑位置与受力位置的布置对结构的综合性能影响也是不可忽视的，因而需要将这两个因素考虑到优化分析中。另外，隐式参数化建模技术多用于白车身的建模，分析与优化中，如文献[2-5]等探讨了隐式参数化建模技术在白车身开发中的应用与优化方法，但是隐式参数化技术在汽车其它结构方面的应用研究较少。

本文以某发动机舱盖为研究对象，利用SFE-Concept软件建立较为详细的发动机舱盖参数化模型，以作为发动机舱盖分析加载或约束的缓冲块位置为变量，研究其位置变化对结构刚度性能的影响趋势，为缓冲块的布置提供依据。同时，再结合发动机舱盖两侧与后部结构断面变量，纵向支撑梁的角度与宽度变量，从结构变化的角度对发动机舱盖进行了多目标的外形与尺寸优化，使得此发动机舱盖结构更加合理。最后，研究了各个变量对各项性能的影响，为后续单项性能的优化提供参考方向。

2 隐式参数化模型与变量定义

2.1 发动机舱盖参数化模型

利用SFE-Concept建模软件，将发动机舱盖结构分解为梁与接头这两种形式的基本模型单元，通过MAP功能建立发动机舱盖中的加强件与内外板之间的连接关系，实现隐式参数化发舱盖的建立，如图1所示。

图1 隐式参数化发动机舱盖模型

2.2 变量的录制

图2 优化变量位置说明

表1 优化变量的变化范围

利用隐式参数化模型的好处之一是可以实现结构各部位在空间中的位置与形状的改变，同时保持各零部件之间的连接关系保持不变，而这些变化可作为优化分析的变量。本文以发动机盖缓冲块位置，发动机舱盖两侧结构断面，发动机舱盖后部结构断面尺寸，纵向支撑梁的位置与宽度为变量，每个变量以5mm为一步进行变量的录制，各变量位置说明图2所示。根据布置要求等相关设计限制，制定的各变量变化范围如表1所示。

2.3 分析工况定义说明

发动机舱盖作为汽车不可缺少的结构之一，对其重量，行人保护，隔热隔音，振动及刚度方面均有要求。本文仅从发动机舱盖的模态及刚度性能角度进行考察与优化。对于模态，考察自由模态，主要关心结构一阶扭转振型下的模态频率，即此发动机舱盖的一阶频率。对于刚度分析，主要以扭转变形与弯曲变形的形式对发动机舱盖刚度进行考察。由于发动机舱盖安装在车身上，其受力主要来自车身，并通过铰链安装点，缓冲块及发动机盖锁将载荷传递到发动机舱盖上，因而，通常情况下，对其刚度的考察一般以这些位置作为加载或约束点。各个刚度工况考察方式如图3所示。

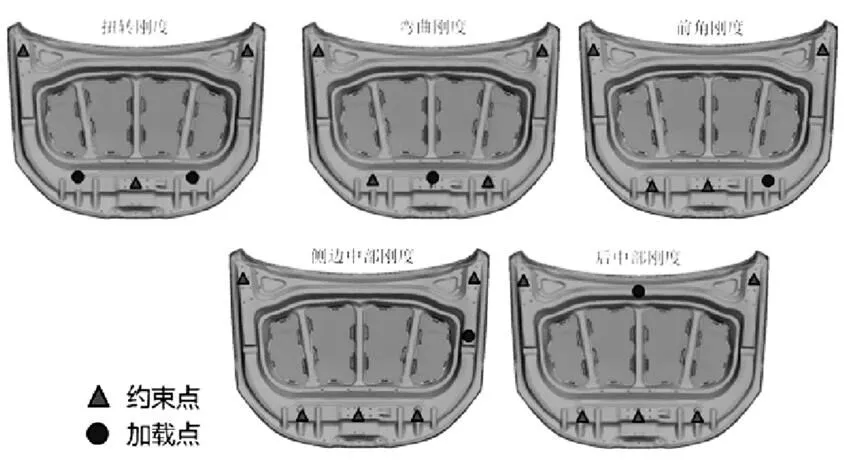
图3 刚度分析工况说明

3 缓冲块位置对刚度性能的影响

3.1 加载与支撑位置对结构刚度性能的影响

由简支梁挠度公式可知，当载荷位于梁的中间位置，且结构的弹性模量，惯性矩以及承受的载荷不变时，如图4所示，其最大挠度与支撑点之间的跨距成三次方正比，跨距越大，最大挠度越大。如公式（1）所示。

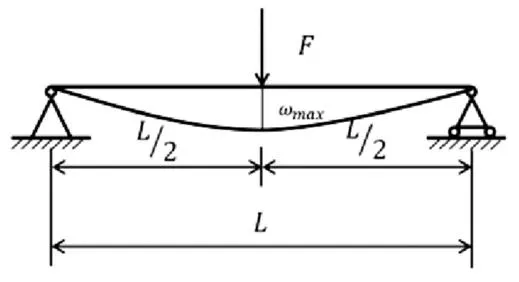
图4 载荷位于简支梁中间

式中：ωmax为最大挠度，E为弹性模量，I为惯性矩，F为载荷，L为左右支撑点之间的跨距。

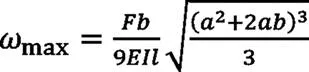
式中：ωmax为最大挠度，E为弹性模量，I为惯性矩，F为载荷，L为左右支撑点之间的跨距，a为载荷距左侧支撑点距离，b为载荷距右侧支撑点距离。

基于以上理论，当结构的支撑位置及载荷施加的位置不同时，其加载点处的挠度是不同的，作为载荷与加载点处的挠度比值的刚度值也不同。因而，合理布置结构支撑位置和载荷施加位置是提升结构弯曲刚度性能的一种手段。

在发动机舱盖设计中，缓冲块位置不属于设计中的硬点，即不可改变的位置，因而可以调整其位置。同时发动机舱盖关闭后需要通过缓冲块与水箱横梁接触，以起到缓冲与支撑作用，其位置的变化范围应考虑水箱横梁接触面的尺寸限制，从而对该变量的变化范围产生限制。

3.2 缓冲块位置对各刚度性能的影响

根据表1中缓冲块X向和Y向变化范围及5mm为一个步距，分别计算出缓冲块沿X向移动和Y向时各个位置下发动机舱盖的各项刚度性能。从分析结果中可以看出，当两侧缓冲块同时沿整车X向移动时，此发动机舱盖的弯曲刚度，前角刚度，侧边中部刚度及扭转刚度均成线性变化趋势，且沿X负向移动，即车前方向移动，其刚度值越低。对后中部刚度来说，基本无影响。从幅值变化程度来看，其对弯曲刚度及前角刚度影响程度较大。如图6所示。

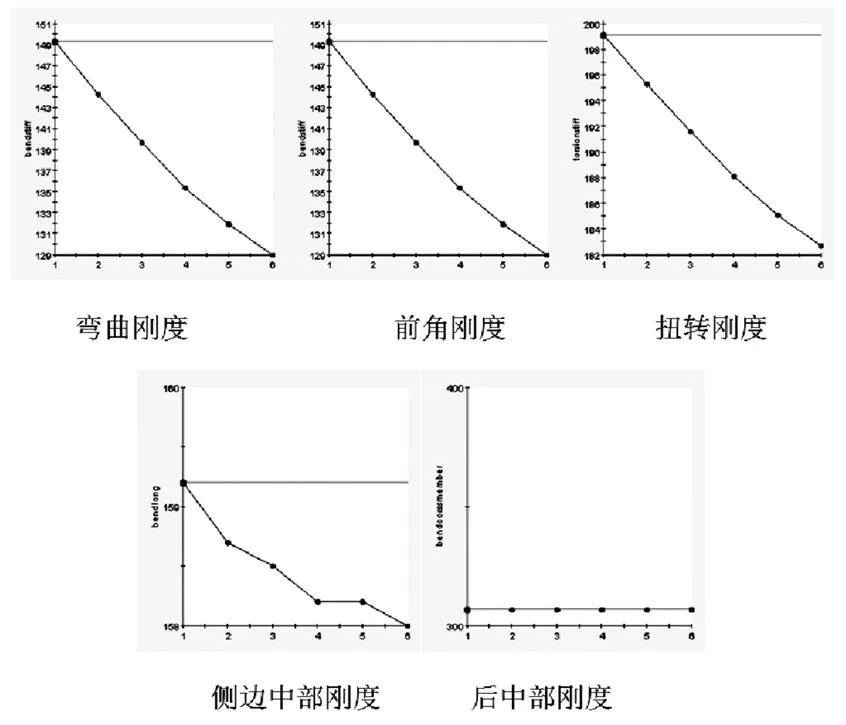
图6 缓冲块X向移动对刚度性能的影响

当两侧缓冲块同时沿整车Y向移动时，此发动机舱盖的弯曲刚度，前角刚度，侧边中部刚度均成线性变化趋势，且缓冲块同时向车内方向移动时，其弯曲刚度值及前角值越高，而侧边中部刚度值越低。对后中部刚度来说，基本无影响。对扭转刚度来说，呈先低后高的抛物线变化趋势。从幅值变化程度来看，其对弯曲刚度及前角刚度影响程度较大。如图7所示。

图7 缓冲块Y向移动对刚度性能的影响

4 发动机舱盖多目标优化分析

4.1 优化流程与优化方法

本文以在发动机舱盖质量不变的前提下发掘初版结构性能潜力以便指导下一轮结构设计为分析目的。基于此思路，该发动机舱盖将以模态及各个刚度考察项的性能最大化为优化目标，以当前发动机舱盖结构的质量为约束条件，进行多目标优化分析，使发动机舱盖的结构布置与尺寸更为合理。

试验设计（DOE）采用优化拉丁超立方设计方法对样本进行抽样，该方法使得所有的试验点尽量均匀地分布在设计空间中，具有非常好的空间填充性和均衡性。考虑到变量数量及各个变量水平数量，样本数量设置为50个，以确保近似模型的准确性。试验流程如图8所示。

图8 试验设计流程

常用的近似模型的构建方法有克里格模型，响应面模型及径向基函数法等，本文经过筛选对比，最终采用二阶的响应面法构建近似模型，并使用交叉验证的方法来考察近似模型的准确性。使用决定系数R2来考察近似模型的整体精度，其越接近1表明近似精度越高，一般大于0.9可满足近似要求[7]。经拟合，各个输出变量的R2值分别为：模态0.994；侧边中部刚度0.991；扭转刚度0.940；前角刚度0.971；弯曲刚度0.974；后中部刚度0.982，质量0.999。

对于多目标优化方法，本文选取非支配排序遗传算法（NSGA-Ⅱ），该方法将目标参数分别处理，并采用标准的突变与交叉遗传算法。筛选过程采用非支配排序和拥挤距离排序两种主要的运算机制[8]。该方法探索性能良好，增强了帕累托前进能力。

4.2 多目标优化分析结果

多目标优化问题的各个目标之间一般是相互冲突的，其最优解不是单一解，设计人员需要从一系列的解集，即帕累托解集中进行权衡取舍，挑选出达到所允许性能要求的一个优化结果。本文经过14407次优化运算并获得740个帕累托解。

表2 多目标优化结果

优化后的最终结构如图9所示。与原始结构相比，左右两侧缓冲块X向位置不变，Y向沿车内方向移动60mm，左右两侧支撑梁前端（车头方向）同时向车内方向移动10mm，后端同时向车内方向移动25mm，且该支撑梁断面尺寸缩小10mm，中间支撑梁断面加宽10mm，发动机舱盖两侧断面尺寸同时加宽10mm，后部断面尺寸减少10mm。

由于优化结果基于近似模型得到，与实际有限元分析结果有一定误差，因而需要基于有限元计算重新获得优化结构的最终性能。该发舱盖最终模态与刚度性能如表3所示。

表3 最终性能结果

从计算结果可知，与原始性能相比，优化后的发动机舱盖结构在弯曲刚度提升33.8%，前角刚度提升28.1%，性能提升明显，对于其他性能来说，变化幅度不大。与表2的近似模型结果相比，误差均在10%以内，说明该近似模型的精度较高。

5 结论

（1）使用SFE-Concept软件的隐式参数化建模技术可以在发动机舱盖早期的开发中构建参数化模型，录制以结构尺寸及布置变化为主的相关变量，快速生成有限元网格进行性能分析，并嵌入到优化流程中探寻性能更优的结构，以指导后期开发阶段的结构设计。

（2）作为发动机舱盖刚度分析的约束或加载位置的缓冲块，其所在位置对刚度性能具有一定的影响。从优化结果中可以看出，缓冲块的Y向位置对弯曲刚度及前角刚度具有较大的影响程度。因而在设计中应合理布置缓冲块等结构支撑与载荷施加位置，充分发挥结构的刚度性能。

（3）经过以缓冲块，纵向支撑梁位置及其他断面尺寸为变量进行的多目标优化分析，使得该发动机舱盖在弯曲刚度的考察中提升了33.8%，在前角刚度的考察中有28.1%的性能提升，其他性能也有不同程度的变化。该优化过程使得发动机舱盖的设计更加合理，尤其在结构本身性能满足的前提下，再次合理优化结构也可为后期轻量化提供更多的减重空间。同时，对各个变量进行各项性能的影响分析可为后期开发中提升单项性能提供优化方向。

[1] 邱忠财.基于全参数化模型的车身结构设计、性能评估及优化[C] // 2015中国汽车工程学会年会论文集,北京:中国学术期刊电子出版社,2015,3:922.

[2] 王磊,刘莹,乔鑫.基于正向开发流程的车身轻量化设计[J].汽车工程学报,2015,5(6):461-465.

[3] 王磊.基于参数化模型的车身结构优化设计// 2016 中国汽车工程学会年会论文集.北京:中国学术期刊电子出版社,2016: 1351- 1356.

[4] 王登峰,蔡珂芳,马明辉,张帅.基于隐式参数化模型的白车身轻量化设计[J].汽车工程,2018,40(05):610-616+624.

[5] Zhou Suwei, LEE M, Cai Hongmei, et al. Upfront Body Structure Development Process Using Parametric Concept Modelling [C]. Proceeding of International Auto Body Congress(IABC), Novi, Michigan, September 19-21, 2006.

[6] 刘鸿文.材料力学(Ⅰ) [M].北京:高等教育出版社,2004:190.

[7] 朱茂桃,郭佳欢,钱洋,刘涛.基于6σ稳健性的车门多学科优化设计[J].汽车技术,2015(12):4-7.

[8] Isight5.6 Component Guide[M]. Dassault Systèmes,2011:182.

Structure Optimization of Engine Hood Based on Implicit Parametric Model

Wang Junfeng, Yin Mingxun, Qiao Xin

（Brilliance Automotive Engineering Research Institute, Liaoning Shenyang 110141）

In order to make the mass and performance of car door reasonable match and determine the reasonable structure of car door in the early design stage, an implicit parametric model of car door is built by using SFE-Concept, part size and position are taken as size variable, and parts thickness is taken as thickness variable. A ulti-objective optimization of the size optimization and thickness optimization is done by using NSGA-Ⅱ optimization algorithm within a single optimization flow. The first mode performance of the door is improved by 12.1%, and the lower stiffness performance of the door is improved by 14.4%. The mass and other performance of the door is basically the same.

implicit parameterization; engine hood; buffer block; multi-objective ptimization

U467

A

1671-7988(2019)14-141-04

U467

A

1671-7988(2019)14-141-04

王峻峰，工程师，硕士，就职于华晨汽车工程研究院，研究方向为结构耐久分析与轻量化分析。

10.16638/j.cnki.1671-7988.2019.14.046