底层柱脚连接方式不同时框架柱计算长度

王金鹏 （深圳市建筑设计研究总院有限公司合肥分院，安徽 合肥 230000）

传统计算长度系数法由于假定较多，且部分假定不合理，导致其精度不理想。文献[1]摈弃了传统计算长度系数法的部分不合理假定，根据平面框架整体屈曲的特点，提出了考虑框架层间相互支援的改进计算长度系数法，并介绍了当框架左右不对称时，采用梁柱合并的方法求解柱计算长度，计算精度很高。但实际工程中，框架左右不对称的问题并非仅限于梁柱截面刚度的不同，或左右承受荷载的大小不同，也存在框架底层柱脚连接方式不同的情况。本文将针对这种情况，继续运用改进计算长度系数法和梁柱合并的方法求解其整体屈曲时的各柱计算长度系数。

1 改进计算长度系数法的简述

为便于使用本文方法，先简单介绍改进计算长度系数法和梁柱合并的方法。如图1所示。

框架底层柱脚均为固端，且左右两侧柱截面和受荷情况对称，据框架各构件线刚度，记求解一元二次方程 aη2+bη+c=0，式中：

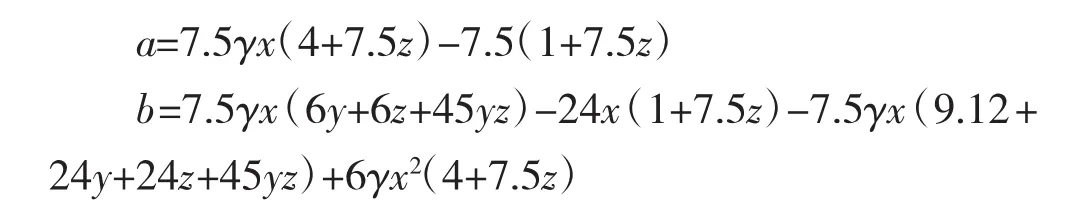
c=24x（6y+6z+45yz）-6γx2（9.12+24y+24z+45yz）

当图1左侧为有侧移不对称框架时，可作梁柱合并处理，将上、下层各柱线刚度合并相加得到各层合并后柱刚度，相应将原结构各柱的梁端约束汇总于合并后的柱端，如图1右侧所示，如此便可按前述对称框架的方法求解合并后各层柱μ值，相应可得各层的层屈曲荷载ΣPcrj，此处便已考虑了层与层相互影响，继而由同层各柱的相互支援的（1）式便可得到合并前各柱μ值。

由此得到的各柱μ值满足（2）式关系。

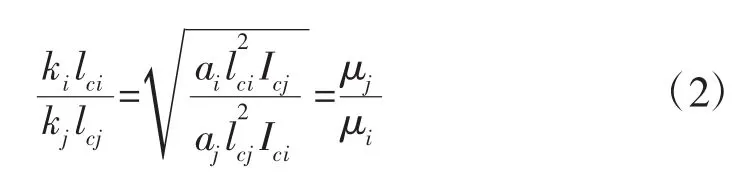
由文献[1]可知该方法精度良好。

2 底层柱脚连接方式不同的不对称问题

当框架左右两侧的底层柱脚连接方式不同时，即如图1所示，底层左侧C点固端，右侧C3柱脚F点改为铰接，求解各柱μ值变得较为复杂。可利用前述方法，将C3柱的线刚度ic3乘以一个刚度折减系数β，使之等效为底层柱脚固端的线刚度为βic3的框架柱参与框架整体屈曲分析，则问题便可解决，关键是该折减系数如何取值，才能使等效前后其他柱μ值变化最小。

本文尝试了两种方案，第一种方案是将图1右侧柱脚铰接的半榀框架取出，将其等效为柱脚固端的型式，等效前后右侧上柱C4柱μ值不变，如图2所示，这就需使等效前后框架E节点处由梁B1提供给上、下柱的约束分配比例不变。E节点处梁提供的总弹簧约束记为mE，对于有侧移框架mE=6ib1，令梁向下柱分配约束为 mE1，向上柱为 mE2，即 6ib1=mE1+mE2。

图2 等效刚度方法

解方程取正值根即可。至此，便将部分底层柱脚铰接的问题转换为柱脚均为固端的问题，按前述方法求解即可，所得其他柱μ值可直接使用，而对于C3柱需结合（2）式求得。该方法需要C3柱K1值足够精确，但上述方法是取出半榀框架来分析求解η值，理论上该值不够准确，不过经过大量试算，发现由该方案求得的各柱μ值与有限元机算所得精确值误差不大，基本在3%以内，精度良好。

第二种方案是由原结构的梁柱线刚度比直接写出C3柱K1值，代入方程（3）求解β值，进而求解各柱μ值，经试算，该方案精度良好，且计算量较小，故推荐使用。

3 几种方案在实例中的验证

以下举部分实例，图1中F点铰接，若lc1=lc2=lb，lc2=lc4=lb1=lb2，ic1=ic3=2ic2，比例加载系数 α1=α2=α3=2α4。按第一种方案，先取右侧底部柱脚铰接的模型计算得 η=6.181，x=2，C3 柱 K1=0.515，代入方程（3）求解，可得折减系数β=0.161，将C3柱转换为线刚度为βic2的底端柱脚固端的柱参与框架整体屈曲分析，按同层梁柱合并求解可得 C2 柱 μ2=1.244，μ1=μ4=1.759，返回原结构由（2）式可得μ3=1.759。对比精确解μ1=μ3=μ4=1.759，μ2=1.269，误差为 -2.0%，较理想。按第二种方案，由原结构图可得C3柱K1=0.333，求解得β=0.135，转换后算得 μ2=1.248，其余各柱因遵从（2）式关系不再列出，误差为-1.7%，精度良好。

若 lc1=lb，lc2=10lb，ic4=ic2，ic3=ic1=2ic2，ib1=ib2=3ic2，仅顶层加载，α1=α2=α3=α4，由第一种方案计算得η=0.851，K1=0.0709，β=0.0493，转换后解得 μ2=1.1223，对比精确解μ2=1.107，误差为+1.5%；按第二种方案，取 K1=1，解得 β=0.195，转换后可得 μ2=1.1226，误差为+1.4%，精度良好。因篇幅关系，其余试例不再列举。

4 结语

从以上分析可知，针对底层柱脚连接方式不同的不对称框架，可以将柱脚为铰接的底层柱刚度折减后转换为底层柱脚均为固端的框架来求解各柱μ值，其中刚度折减系数β可按文中介绍的第二种方案计算，由原结构的梁柱线刚度比直接得到C3柱上端K1值，代入方程（3）求解β，再按改进计算长度系数法和梁柱合并的方法求解各柱μ值，该方法仅需初等代数运算即可得到精度良好的解。