基于变分模态分解的地震随机噪声压制方法

方江雄 温志平 顾华奇 刘 军 张 华

(①东华理工大学核技术应用教育部工程研究中心，江西南昌 330013；②东华理工大学地球物理与测控技术学院，江西南昌 330013；③江西省基础地理信息中心，江西南昌 330209)

0 引言

地震信号随机噪声衰减是地震数据处理领域的热点和难点问题。从观测数据中有效去除随机噪声干扰、提高信号信噪比和分辨率，是正、反演计算和地质解释的前提。目前，学者们提出了大量的地震信号随机噪声压制方法，比如基于滤波理论的方法[1-2]、基于小波域变换方法[3-6]、基于矩阵理论的变换方法[7-10]、基于信号分解理论方法[11-16]等。近年来，由于在处理非平稳及非线性数据上具有很高的信噪比，基于信号分解的经验模态分解(Empirical Mode Decomposition，EMD)方法[17]已成为信号分解领域研究的热点。

学者们在EMD方法基础上，进一步提出两种经典的改进方法，即集合经验模态分解(Ensemble EMD，EEMD)[18]和完备集合经验模态分解(Complete EEMD，CEEMD)[19]。其中，EEMD避免了EMD方法中的模态混叠，而CEEMD改善了EEMD方法中因辅助噪声造成的噪声污染。但是，CEEMD方法中依然采用递归迭代式筛选分解过程，非平稳地震信号极值点插值和包络计算过程耗时过长，在处理多维度和多尺度地震数据时存在一定限制。为了解决这些问题，以进一步提升信号分解的精度，本文提出全新的非线性、非递归的完全自适应时序序列分解算法——基于变分模态分解(Variational Modal Decomposition，VMD)的地震信号分解方法，并应用于二维和三维地震数据随机噪声压制中。

1 基本原理

VMD的基本思路是：在EMD的固有模态函数(Intrinsic Mode Function，IMF)分量基础上，引入更严格的频率域带宽先验约束(Band-Limited Intrinsic Mode Function，BIMF)信号，又称带限分量，解决EMD中模态混叠和高频率信号丢失问题。IMF被定义为在信号极值点个数和过零点个数相等或相差一个时，任一时刻点由局部极值点所确定包络均值为零的信号。

VMD基本原理是： 在IMF信号分量基础上，通过引入调幅—调频(AM-FM)信号

uk(t)=Ak(t)cosφk(t)

(1)

式中：Ak(t)和φk(t)分别为uk(t)的瞬时幅值和瞬时相位。φk(t)为非减函数，即瞬时角频率

(2)

与φk(t)相比，Ak(t)和ωk(t)的变化较为缓慢，即在短时范围内可认为是一个幅值和频率不变的谐波信号。将满足上述条件的BIMF赋予具体的物理意义，即VMD将输入信号自适应分解成有限个BIMF分量之和，分解过程满足每个带限BIMF分量的估计聚集带宽之和为最小。与传统EMD方法不同，在获取BIMF分量时，VMD方法的递归迭代筛选模式将信号的分解过程转换至变分问题的求解，在寻找变分模型最优解的过程中完成信号的自适应分解。

2 地震随机噪声压制

2.1 地震信号的域表示

线性地震数据可表示为

(3)

式中：t和x为时间和炮检距轴；w为地震子波函数，如Ricker子波；c为波在介质中的传播速度。将同相轴数据沿t(时间轴)作傅里叶变换，将t-x域转换到f-x域，得到原始数据的f-x频谱

(4)

将式(4)进行离散化，即可得到D(f-x)的离散表示

Df(m)≡D(f,mΔx)m=1,2,…,M

(5)

式中： Δx表示沿x轴方向的道间距；m为地震采样道数，M为总道数。统计相邻两道可表示为

(6)

式(6)是一阶递归微分方程，对应每一个频率切片Df(m)信号，由一个复调和谐波函数(调幅—调频)组成。因此，通过在t-x域中的无噪声线性数据中找到递归系数ei2πfΔx/c，使其在f-x域中完全可预测。类似地，t-x域中N个线性事件的叠加相当于f-x域中的N个复数谐波的叠加。

2.2 VMD框架求解

基于上述地震数据域分析，在频率域中估计BIMF分量频率带宽目标函数[20]

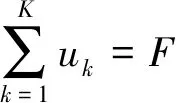
(7)

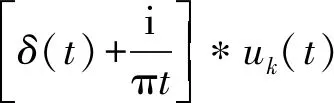
通过将VMD方法的变分优化框架(式(7))拓展至复数空间，而复数空间正弦信号的傅里叶频谱是单边的，因此式(7)改写为

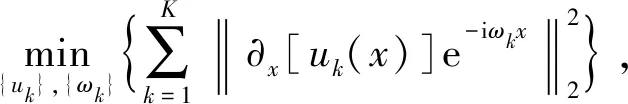
(8)

为求解式(8)中变分问题，采用增广Lagrange函数[14]计算其最优解。通过引入二次惩罚因子α和拉格朗日乘法算子λ，将约束性变分问题转换为非约束性变分形式

(9)

式中：L(·)表示目标函数；“∶”是一个函数的标记；〈·,·〉表示內积；二次惩罚因子α是控制数据保真度的均衡参数，用于平衡变分正则项和二次约束项，在含噪声情形时可保证信号重构精度；λ可以保证模型约束条件的严格性。

采用交替方向乘子算法 (Alternate Direction Method of Multipliers，ADMM)[22]求解式(9)，具体步骤如下：

(2)n=n+1，执行主循环；

(3)Fork=1∶K-1，执行第一个内循环更新uk

(10)

(4)k=K，结束第一个内循环；

(5)Fork=1∶K-1，执行第二个内循环更新ωk

(11)

(6)k=K，结束第二个内循环；

(7)对于所有ωk>0,k∈[1,K]， 双重对偶上升，更新λ

(12)

式中τ表示噪声容限参数。在噪声压制任务中(而不是信号的重构)，更新参数τ=0以得到更好的去噪效果；

(8)给定判定精度ε>0,k∈[1,K]， 重复步骤(2)～(7)，直至满足迭代停止条件

(13)

(9)结束迭代，即得到K个带限BIMF分量。

从上述步骤可知，ADMM的求解过程包含VMD的模态和频率中心更新。其中，ωk的更新由对应模态的能量谱重新得到，uk模态更新对应于1/βω2的Wiener滤波器结构(β为白噪声方差，1/ω2表示信号的能量谱为低通形式)。参数α控制着Wiener滤波器的宽度，本文称为保真度均衡参数。增大α值，Wiener滤波器宽度变窄，可以滤除更多的噪声，但也使得BIMF分量包含更少的真实信号峰值信息，同时算法趋于发散不收敛的几率增加，反之亦然。式(7)的增广Lagrange函数形式与Tikhonov正则一致，具有保真项和正则项。其中，VMD方法中分解的带限BIMF分量具有明显的稀疏特性，因而正则项可用稀疏先验。α与正则参数类似，用于控制保真项和正则项的权重，使BIMF模态分量的更新公式(式(10)～式(12))具备Wiener滤波特性，这正是VMD方法具有较强抗噪性能的关键因素。

2.3 基于VMD的二维地震信号去噪方法

根据上述理论，基于VMD方法的二维地震信号随机噪声压制处理算法流程如下：

(1)选择一个时间窗口将原始含噪地震信号d(x,t)作傅里叶变换至f-x域；

(2)对每一个频率切片数据进行复数VMD分解；

(3)将VMD分解得到的BIMF分量组合得到滤波后的信号；

(4)将信号作傅里叶逆变换回t-x域；

(5)对下一个时间窗口重复以上操作，地震记录全部处理完毕后，即得到最终的二维地震去噪结果。

2.4 基于VMD的三维地震信号去噪方法

在三维地震数据中，平面波可表示为

(14)

式中：x=(m,h)为中心点和炮检距坐标；n为波的传播单位方向。三维地震模型的频率切片Df是由沿n方向的一个f-m-h域复谐波模式组成。将d(t,x)沿时间轴上作傅里叶变换得到f-m-h谱，每个频率切片数据即为Df。相应地t-m-h域中p个平面波的叠加与f-m-h域中p个复谐波叠加等效。本文将二维VMD拓展到复值，拓展后的目标优化函数为

(15)

式中vk为二维平面的波数向量。与一维VMD求解类似，通过引入二次惩罚和拉格朗日乘数(增广Lagrange)重建约束变分框架，由ADMM优化求解，二维VMD的三维地震随机噪声压制算法步骤如下：

(1)选择一个时间窗口将原始含噪地震信号d(m,h,t)作傅里叶变换至f-m-h域；

(2)对每一个频率切片数据进行二维复数VMD分解；

(3)组合VMD分解的BIMF分量得到滤波后的信号；

(4)将信号作傅里叶逆变换回t-m-h域；

(5)对下一个时间窗口重复以上操作；

(6)地震记录全部处理完毕后，即得到最终的三维地震去噪结果。

3 算例

3.1 VMD参数优选

VMD变分模型目标函数是非凸的，算法的收敛性与参数的设置有密切联系，有三个重要参数，即带限BIMF分量个数K、ωk和α。其中，K依据BIMF分量瞬时频率均值的极大值点确定；ωk采用匹配追踪算法(Matching Pursuits，MP)[23]确定；α与原始信号的噪声水平有关，用来控制保真项和正则项的权重，本文采用“L”曲线法则确定α。为验证VMD方法的有效性，本文将三个不同中心频率余弦信号累加构成合成信号s(t)

(16)

图1a、图1c、图1e显示了合成信号s(t)经VMD分解得到的3个BIMF分量信号，图1b、图1d、图1f分别为上述相应的BIMF分量信号局部放大结果。从分解结果可以看出，各个BIMF分量信号与原始组分信号几乎一致，仅在信号两端点处出现微小误差。

图2为原始合成信号的频谱分布与VMD分解后的3个BIMF分量信号的频谱图(双对数坐标)，每个重构BIMF模态分量的频谱都有一个最高峰值，对应其中心频率，与原始信号的期望中心频率2、24、288Hz高度一致(非等间距横坐标)，VMD分解得到的3个BIMF分量均能成功捕捉对应中心频率。

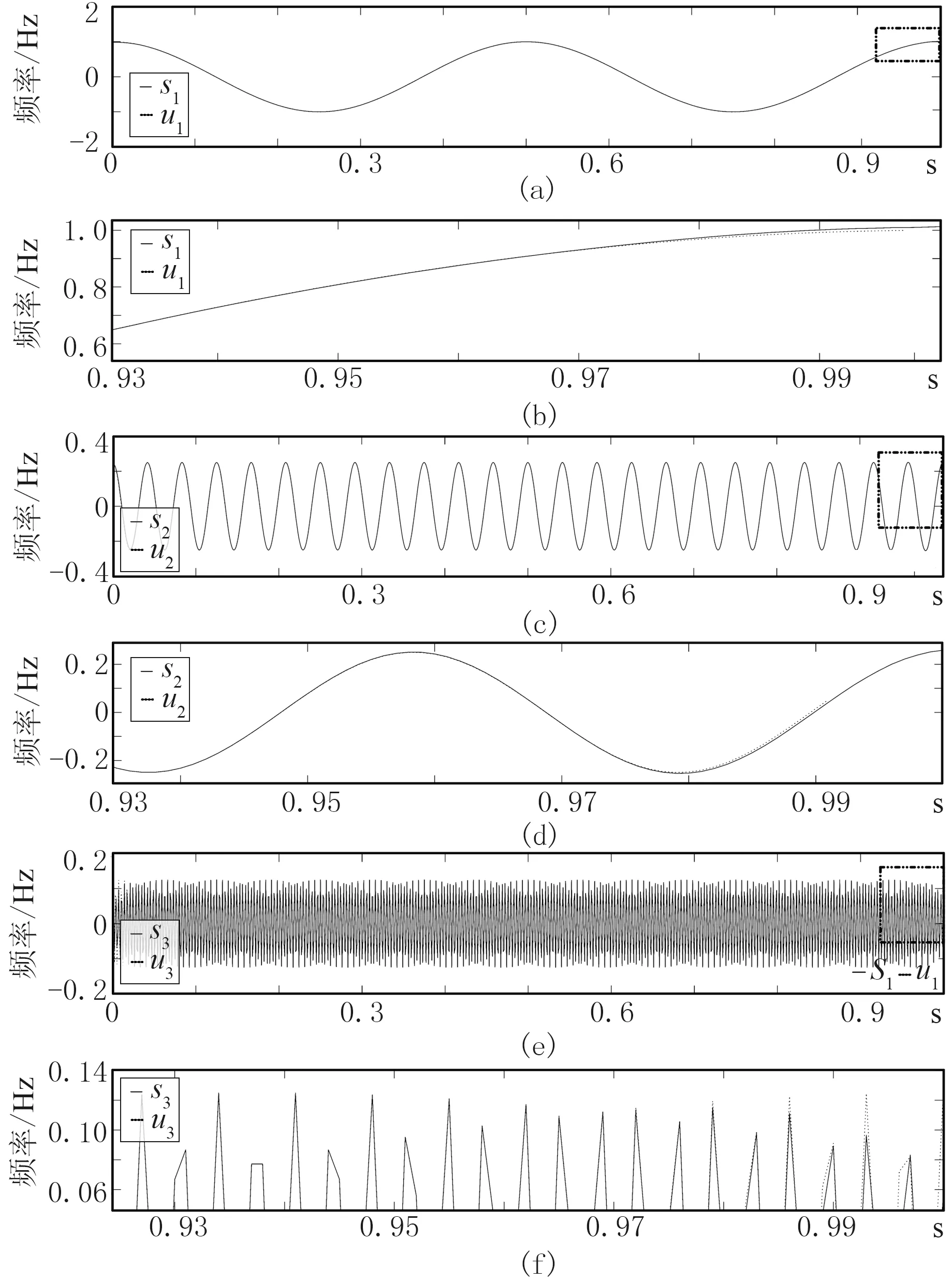
图1 各组分信号及VMD分解BIMF分量

图3为分解各模态信号的频率中心随迭代次数的变化曲线(半对数坐标)。由图可见，图3a迭代更新过程较慢，在150次后才找到最优的中心频率，而图3b经3次迭代即可获得最佳频率中心分布。

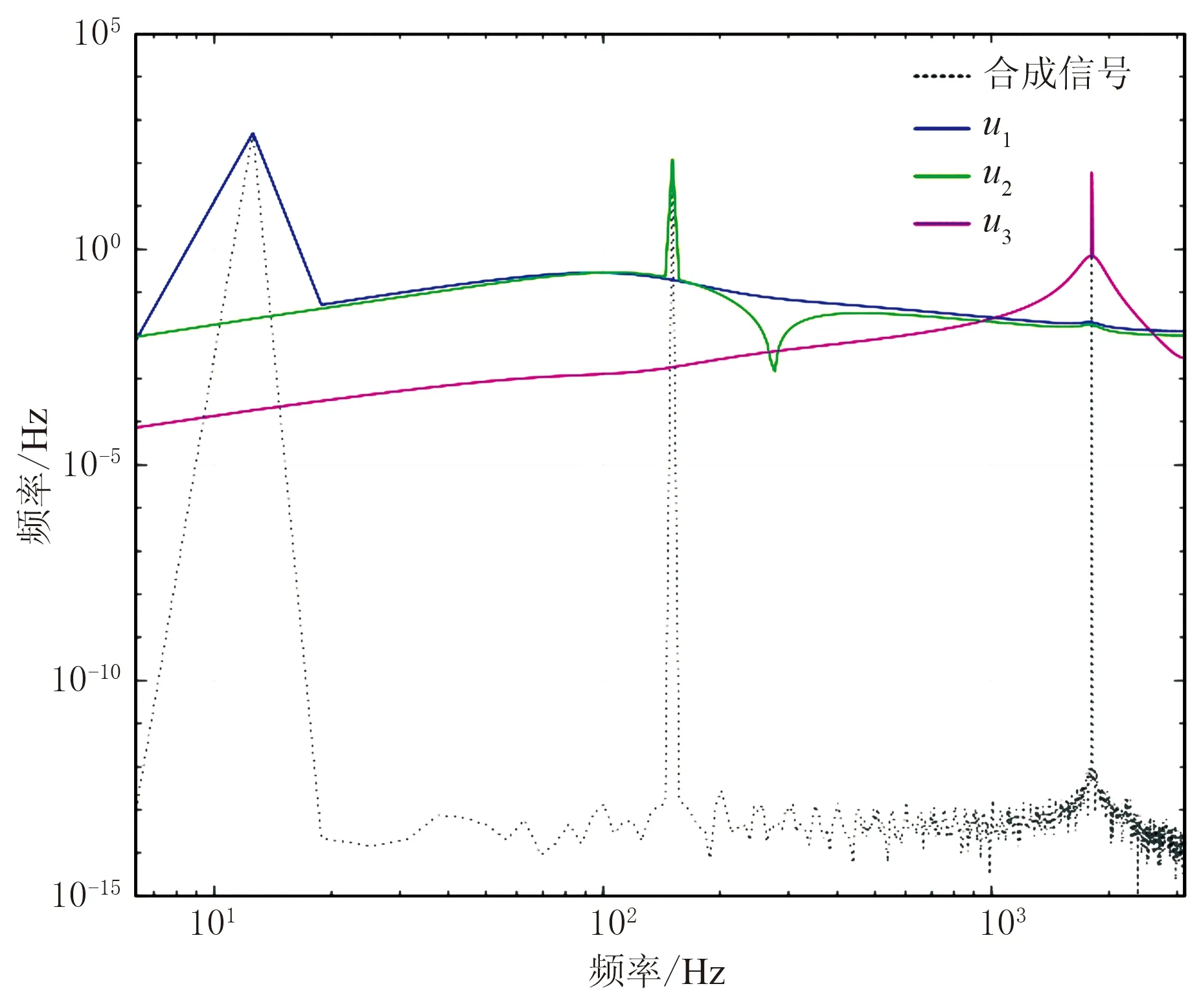
图2 VMD分解各模态频谱分布

图3 VMD分解各模态频率中心变化

图4 合成地震数据(左)及加噪数据(右)频谱对比

图4是一组由四个线性事件组成的合成地震数据、加噪数据及其对应的f-x频谱图、f-k频谱图。对图4b中第40个采样点切片含噪数据作VMD分解，结果如图5所示。设置参数α=2000，K=4，以匹配追踪算法初始化ωk分解得到四个近似谐波信号，各个BIMF分量的频谱与原始信号的频谱峰值高度一致。

3.2 二维地震去噪实例

本文采用信噪比(SNR)、 局部相似度(Local Similarity，LS)[24]、 结构相似度(Structural Simila-rity Index，SSIM)[25]评价算法的有效性。局部相似度定义为

(17)

式中： T表示转置；c1、c2通过最小二乘问题最小化得到

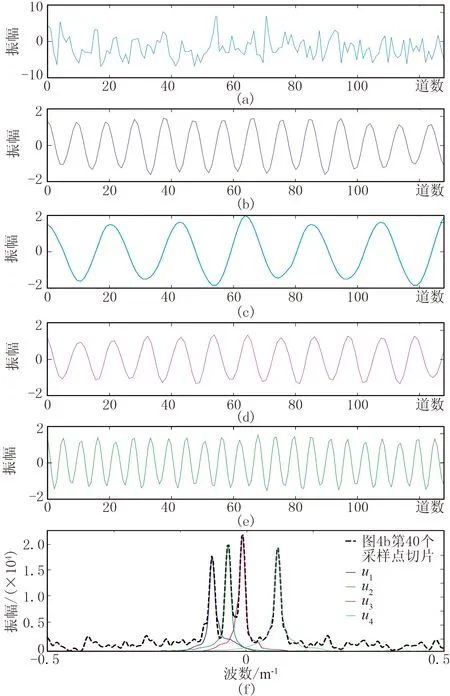
图5 含噪f-x谱第40个采样点切片数据作VMD分解

(18)

(19)

式中：a和b为矩阵；A、B分别为a、b构成的对角算子。LS值变化范围为[0，1]，LS值越大表示去噪结果与噪声剖面的局部相似程度越高，有效能量泄漏越严重，算法的幅值保持能力越差。

结构相似度定义为

(20)

式中：μx、μy分别表示图像x、y的均值；σx、σy分别表示图像x、y的标准差；σx、σy分别表示图像x、y的方差；σxy代表图像x和y的协方差；C1、C2为常数，C1=(k1L)2，C2=(k2L)2，L为像素动态范围，一般k1=0.01、k2=0.03、L=255；SSIM值变化范围为[0，1]，值越大表示两个图像的结构相似程度越高，去噪性能越强。

图6表示一个含有多层倾斜地层、一个不整合面、一条断层和多套正弦起伏形态地层组成的理论合成地震记录Sigmoid模型[26]，含256道，每道有256个时间采样。为验证VMD方法的有效性，本文将VMD与Curvelet(曲波)、NLM(非局部均值)、BM 3D(三维块匹配)、CEEMD四种方法进行对比。

图6 合成地震记录Sigmoid模型

在本实验中，VMD方法中K=4，α=2000，ωk初始化采用匹配追踪方法，时间轴窗口长度取64个采样点，空间轴窗口长度取64道，时间轴和空间轴的滑动步长重叠度均设置为50%；CEEMD方法集总次数I取100；Curvelet、NLM和BM3D三种方法采用工具包中的默认参数。算法运行平台参数为MATLAB 2017a Parallel Pool×8、Win 10×64、i7-7700K CPU 4.2GHz。

图7a～图7f左图为地震数据加噪后用不同方法去噪的结果，右图为相应的噪声剖面局部相似度。由图可知，五种方法均达到一定的去噪效果，但Curvelet方法去噪结果有一定的变形，在正弦状起伏的强反射同相轴周围发生明显伪影现象，断层现象不明显，弱反射同相轴连续性差，对应的局部相似度图表明有效能量泄漏明显(图7b)；NLM去噪结果中仍保留有肉眼可视的噪声信息，对应的局部相似度图表明线性和双曲线有效能量均出现泄漏，对原图像的结构信息保护不够，这与NLM算法中在计算图像块相似性时只考虑块的平移特性有关(图7c)；相对Curvelet和NLM方法，CEEMD方法在SNR数值上有些提升，但去噪结果中仍保留部分噪声信息，断层部分尚可辨识，对应的局部相似度图在正弦状起伏的强反射同相轴有些许能量损失(图7d)；BM 3D方法的去噪效果较好，但也可见部分低能量有效信号被当做噪声被去除(图7e)；VMD的去噪结果中SNR提升最为明显，优于其余四种方法，合成模型中的倾斜、正弦状起伏地层以及断层位置都得到了很好的保留，噪声得到有效压制，视觉表现上与原始无噪模型最为接近。对比局部相似度图可知，VMD方法有效能量泄漏程度最轻微，保真度性能最好(图7f)。

图8给出了五种方法的第175道信号去噪结果对比，可以看出VMD去噪结果与无噪信号最为接近。因此，VMD方法在去除强噪声的同时，可最大程度的减少有效地震能量的损失。

Curvelet、NLM、BM 3D、CEEMD和VMD五种方法处理耗时分别为0.724、11.291、181.039、2.207和2.513s，Curvelet去噪处理效率最高，BM3D处理效率最低。

图7 Sigmoid模型五种方法去噪结果(左)及相应的局部相似度(右)

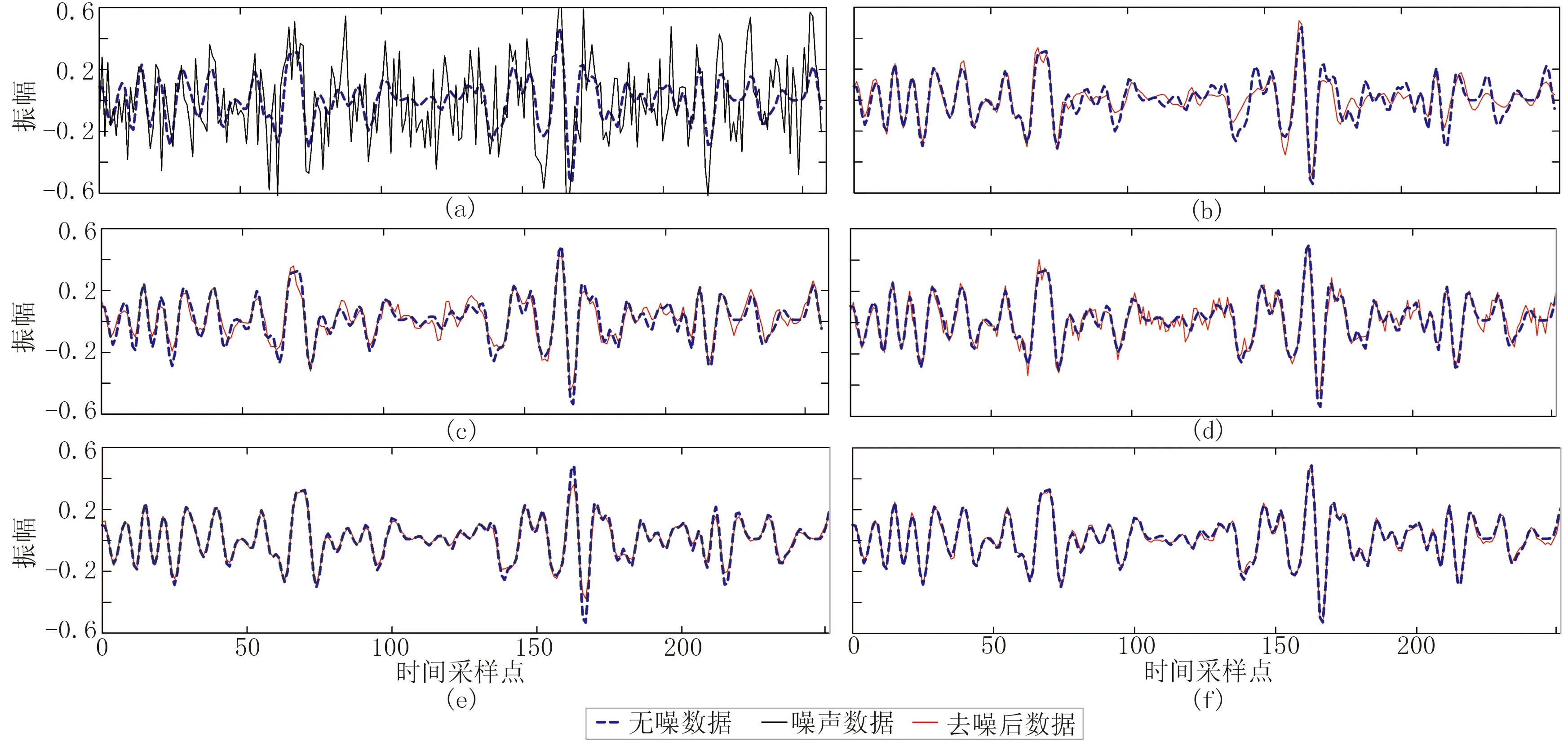
图8 Sigmoid模型五种方法第175道去噪结果对比

3.3 三维地震去噪实例

处理效率是考虑算法是否适用的重要指标，在三维甚至五维地震资料的随机噪声压制处理中，尤其需考虑计算耗时。本文将Curvelet 3D、NLM 3D、BM 4D和二维VMD(VMD 2D)四种方法运用于三维实际含噪地震数据处理。取某地随机噪声分布较多的三维叠后实际资料，数据尺度为221×271×752(依次表示x、y和时间三个方向的采样点数)，采样间隔分别为20m和4ms。取实际数据x、y方向的第100个切片，如图9所示。

图10为四种方法去噪结果，图11为相应的噪声剖面局部相似度图，去噪结果与噪声剖面的局部相似程度越高，表明有效能量泄漏越严重。对比各图可知，Curvelet 3D方法去噪结果过于平滑，同相轴边缘细节信息模糊，较难辨别，对应局部相似度表现较多的有效能量损失；NLM 3D方法去噪结果中局部块状细节消失，可见部分噪声依然分布于去噪结果中，对应局部相似度出现较多的局部高异常区域；BM 4D方法的去噪效果有所改善，剖面视觉效果较好，局部相似度表现为有效信息损失少；本文二维VMD 2D方法的去噪结果最优，剖面上同相轴细节、断裂走向清晰，局部相似度呈低能均匀分布，有效同相轴信息丢失最少。

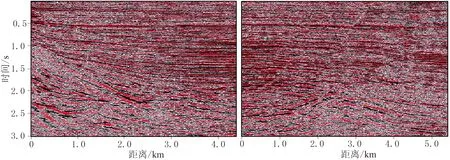
图9 三维叠后含噪实际地震剖面

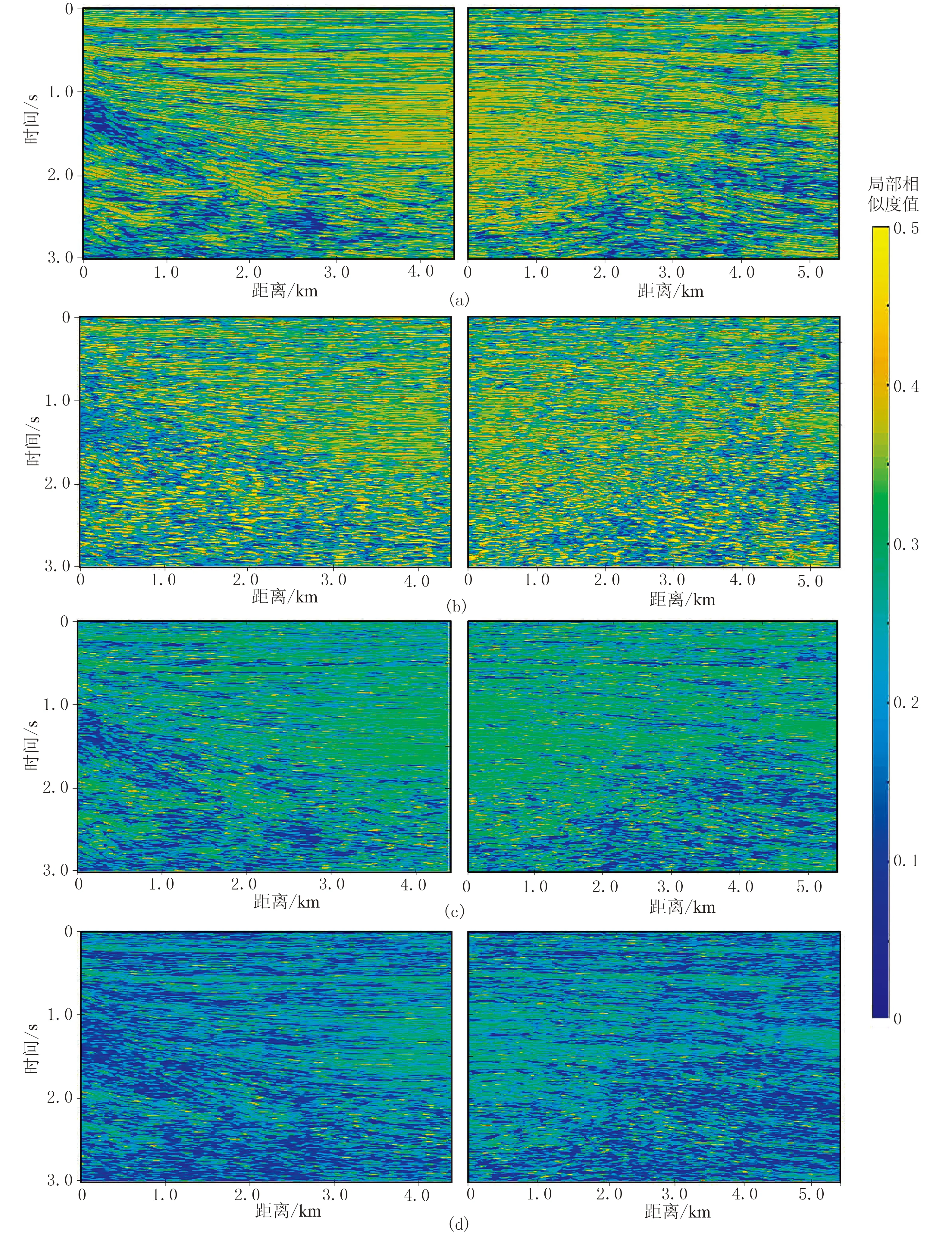
图11 三维实际资料去噪后噪声剖面的局部相似度

Sigmoid模型和实际资料的去噪结果数值统计如表1所示，可见Curvelet方法的SNR数值提升最小，但时间效率最高；CEEMD方法处理耗时最长；与CEEMD递归式模态分解方法不同，VMD在变分框架约束下一次性求解得到所有带限BIMF分量，在SNR和SSIM指标上均达最优，去噪结果与原始无噪信号在细节上最为接近。由于在匹配追踪优化下快速定位到频率中心，VMD方法时间效率高于NLM、CEEMD和BM 3D方法。三维实际地震资料的去噪结果LS同样验证其有效性。因此，VMD方法具备优异的噪声压制、幅值保持性能的同时，还有具有较高的计算效率，可以满足实时处理要求。

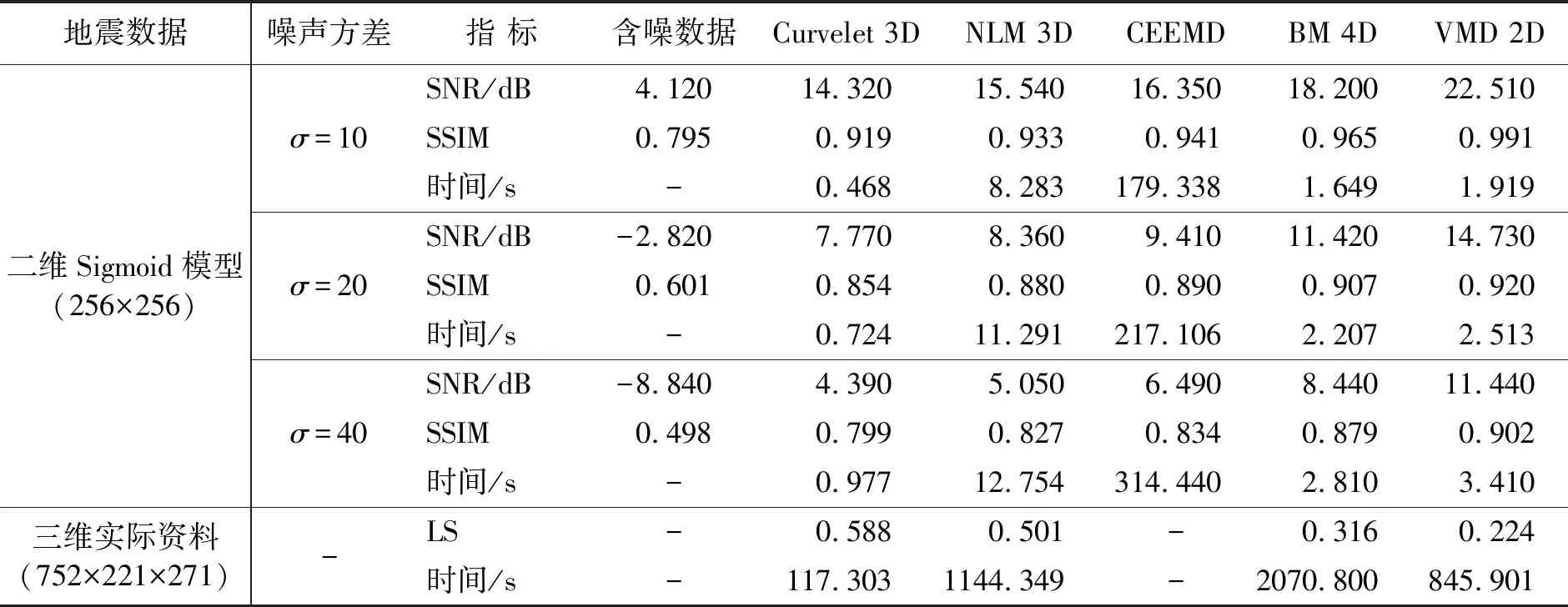
表1 去噪结果统计

4 结束语

本文在EMD信号分解理论基础上，提出了在频率域内复数VMD方法。通过将信号分解过程转移到变分框架内，引入增广Lagrange函数迭代求解各分量的频率中心及带宽参数，生成窄带约束模态分量，使VMD方法在噪声压制和有效能量保持间寻求最优平衡。实验结果表明，在二维地震数据的随机噪声压制处理方面，与CEEMD、Curvelet、NLM和BM 3D方法相比，VMD方法在SNR、SSIM和视觉效果方面均保持最优趋势，处理后同相轴细节变得清晰连续，微弱信号被有效保留；在三维地震数据的随机噪声压制处理方面，与Curvelet 3D、NLM 3D和BM 4D方法相比，VMD方法具备优异的噪声压制性能且计算效率高。