一项高效的折射静校正技术

肖永新 杨海申 崔士天 徐丽军 赵薇薇 马 洁

(东方地球物理公司采集技术中心，河北涿州 072751)

0 引言

折射静校正是根据地震资料中单炮的折射波初至时间，计算折射层速度、延迟时及近地表厚度，进而得到静校正量的一种常规静校正方法。1919年德国人Mintrop首先在石油勘探中运用了折射法[1]。折射波方法早期应用大多是针对浅层折射波资料的解释。Hagedoorn[2]根据几何地震学原理，给出了一种用相遇观测系统折射地震资料求取水平均匀折射界面的几何作图法——加减法，并应用该方法成功地解决了浅层折射波解释和地震反射勘探中的风化层校正问题；Gardner[3]提出将截距时间分解成激发点和接收点两个延迟时分量的思路；Barthelmes[4]提出了延迟时间法(或时间项法)；Scheridegger等[5]提出了时间项法即分解法；Hawkins[6]提出互换法，该方法能简捷地确定折射层结构和速度变化；Palmer[7]提出的广义互换法(GRM)可利用相遇剖面处理很不规则的折射层；基于GRM，Bahorich等[8]提出扩展广义互换法(EGRM)和ABCD法；陈广思[9]提出了相对折射静校正技术，潘红勋等[10]对此进行了改进。

经过近百年的发展，折射静校正理论趋于完善，近年来发表的折射静校正的文献很少有理论上的创新，基本都是探讨算法改进或报道应用实例。例如： Bridle[11]以加减法为基础求得非线性的延迟时解；Law等[12]提出了一种稳健的结合反射数据的折射静校正方法。

涉及折射静校正技术的应用软件研发也持续了数十年。绿山公司早在20世纪90年代就推出了折射静校正应用软件；业界其他知名处理软件系统(如CGG、OMEGA、PROMAX、FOCUS等)也纷纷推出各自折射静校正算法；2000年，石油物探局(BGP)发布了克浪折射静校正软件。这些折射静校正软件在业界得到广泛应用并取得良好效果。但究其基本原理，都是上面提到的互换法、时间项法及广义反演等算法。

随着勘探领域的拓展，所面临的近地表问题越来越复杂，勘探数据量也呈几何级数增长。近十年来，越来越大的数据体导致处理一套折射静校正量动辄需要几周的运算时间甚至导致软件长时间无响应。绿山、克浪等一系列折射静校正软件越来越难以满足现阶段数据采集现场处理要求。另外，从实际地震资料处理情况看，目前还没有一种静校正方法能完全解决所有静校正问题，复杂地区需多种静校正方法协同解决静校正问题，而折射静校正是其中不可或缺的一种方法[13-15]。

为此，本文从折射静校正的基本原理出发，充分汲取前人研究成果，探究并建立了一套针对海量地震数据的高效、实用的折射静校正技术系列。

1 折射静校正原理

折射静校正是以折射波传播理论为基础的一种成熟的且适应性广泛的静校正方法，这种方法充分利用初至波中包含的丰富的近地表信息，统计得到准确的长、短波长的静校正量，是解决复杂地区静校正问题的一种常规手段。折射静校正的计算原理简单易懂，但为了便于对后续内容的理解，本文简要介绍基本折射方程、折射速度计算原理及延迟时计算方法，其他折射静校正的原理及实现过程如：层位划分、模型建立、静校正量计算等功能采用常规方法就能够满足效率需求，本文不再赘述。

1.1 基本折射方程

单界面水平层状介质中折射波传播路径及时距曲线如图1所示，经推导可得折射波时距曲线方程[16-20]

(1)

式中：t为折射波旅行时；x为炮检距；v0、v1分别为风化层和折射层速度；h为风化层厚度；θ为临界角。

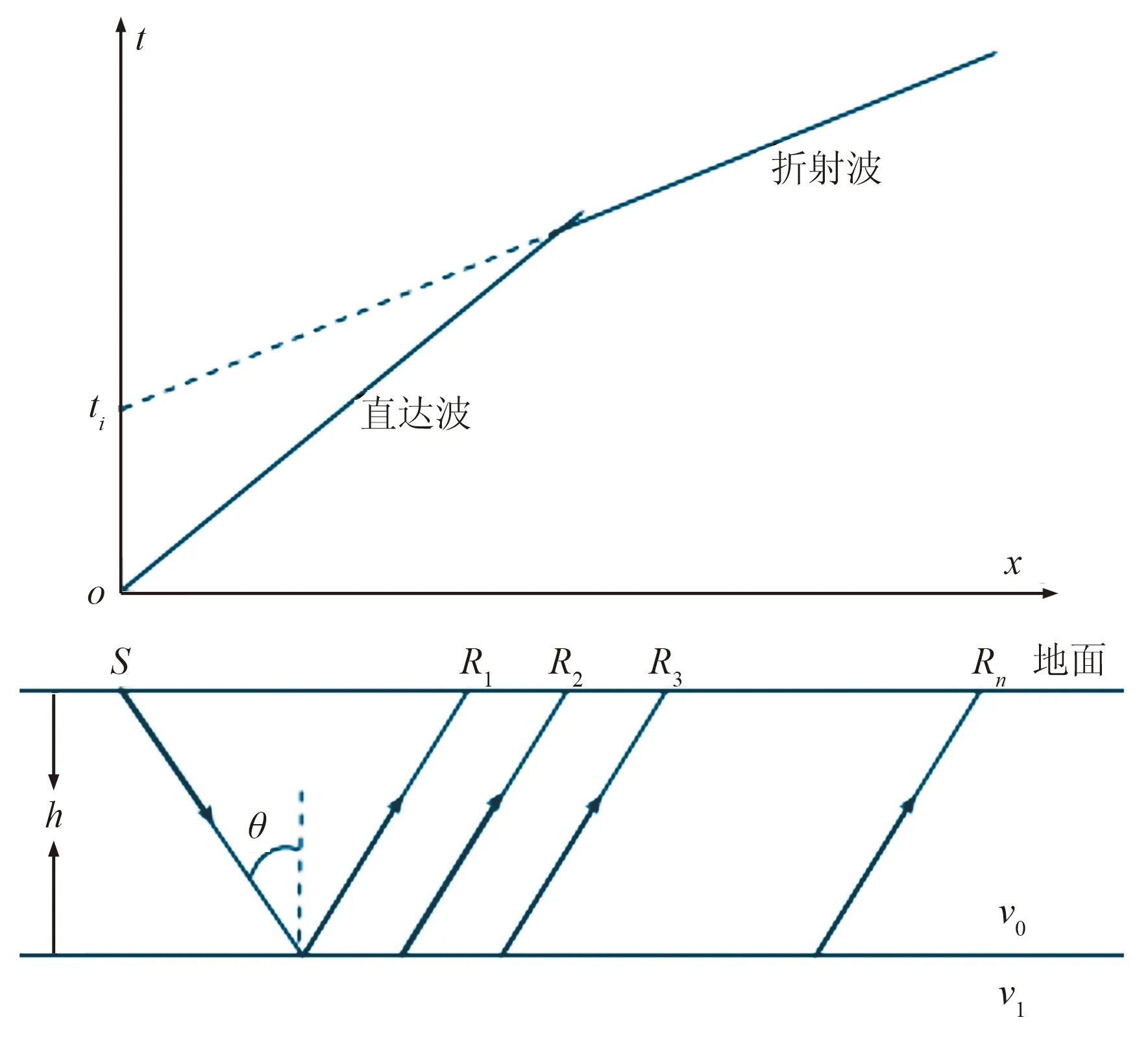
图1 单个水平界面折射波时距曲线示意图

对该折射波时距曲线方程做简单变形，可得基本折射方程

(2)

式中：ts为炮点延迟时；tr为检波点延迟时。显然，该式表明折射波初至时间由三部分组成，即炮点延迟时、检波点延迟时和沿炮检距的滑行时间。

1.2 折射速度计算原理

折射静校正计算过程中，若排除计算机硬件因素、人为因素的影响，折射速度计算效率是影响其运算效率的最重要因素，因此要提高折射静校正计算效率，提高折射速度计算效率是至关重要的。

折射速度计算是选择合适炮检距范围内的初至信息，通过拟合算法或互换算法进行计算的。拟合法是在CMP域或共炮域内，在炮检距—时间坐标系中，用直线拟合初至，直线斜率的倒数就是折射波的速度值。拟合初至得到折射速度，具有计算速度快的优点，但是计算得到的折射速度精度受地表起伏、地层倾角等因素影响严重，所以在实际生产中很少使用。

用互换法计算折射速度。图2中A、B为炮点，R1、R2、…、Rn为可同时接收来自炮点A和B的折射波的接收点，表层速度为v0，折射层速度为v1。

图2 二维折射波传播示意图

根据基本折射方程，炮点A到接收点R1、R2、…、Rn的初至时间可表示为

(3)

(4)

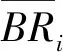
由式(3)、式(4)得到

(5)

在ΔX—ΔT坐标系中(图3)，用直线拟合散点，同样该直线斜率的倒数即为待求的折射波速度值。这样可消除折射界面起伏和接收点不严格在一个平面时的影响，从而计算出准确的折射速度。该方法同样适用于三维施工(图4)情形，两炮点共同的接收点可来自多条接收线。

图3 折射速度计算示意图

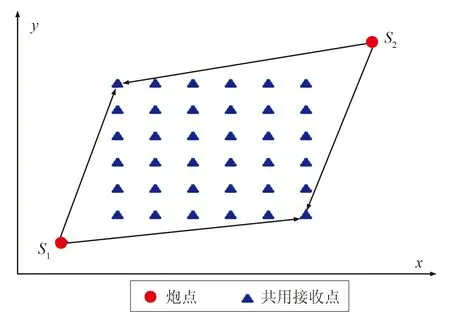
图4 三维速度计算示意图

互换算法一直是折射速度计算的主流算法，具有计算精度高的优点。常规方法是利用任意两炮点共用的检波点计算折射速度，导致其计算量巨大，计算效率难以满足实际需要。

1.3 延迟时计算

延迟时是折射静校正中一个重要参数，延迟时计算结果直接影响近地表模型的建立及静校正量的计算精度[18]。延迟时的计算方法很多，本文介绍高斯—赛德尔迭代算法。

由基本折射方程(式(2))可得

(6)

式中： 炮检距x可以通过坐标计算得到；折射速度v1在速度计算后已知，因此式(6)中只有炮点延迟时ts和检波点延迟时tr两个未知数。

对于每一炮的每一道初至来说，都可写成式(6)的形式，即每个炮检对都可列出这样一个方程，就可得到一个大型的超定方程组，解此方程组即可得到每个炮检点的延迟时。在本文所述的折射静校正方法中采用高斯—赛德尔迭代算法求解方程组，此算法具有运算速度快、收敛迅速、计算结果稳定等特点，一般迭代3～4次即可得到稳定的结果。在计算过程中，还充分考虑到激发点深度、炮检点组合等因素的影响，从而提高了延迟时计算结果的精度。

2 实现方法改进

折射静校正中影响计算效率的因素很多，折射速度计算与延迟时计算是最重要的两个因素，这两个过程都需读取初至文件，初至文件占用内存大、初至数据提取效率低等问题都严重影响了计算效率。

2.1 高效的初至数据管理

折射静校正的计算过程就是对初至时间的处理过程，其中不可省略的读写初至的步骤有： ①加载初至时，需要读写共炮初至；②折射分层时，需要读入共中心点初至；③计算折射速度时，需要读入共炮初至；④计算延迟时，需读入共炮和共检初至。

对初至数据的读、写几乎贯穿整个折射静校正的计算过程，所以初至读、写的效率决定了折射静校正的计算效率。以前炮道密度较小，一个工区的初至数据量不大，所以初至文件的读、写效率对折射静校正计算效率的影响较小。但近年来，炮道密度动辄上百万，甚至达千万，初至数据骤然变得巨大，初至文件读写效率对折射静校正计算效率的影响日益凸显。以往的折射静校正软件运行效率很低，折射分层时显示一个或多个网格的共中心点初至就需耗时几分钟，交互分层后还需等待几分钟软件才有响应，这样仅在定义分层控制点这一环节就需大量耗时；而计算折射速度时，数据稍大就会造成软件系统几天甚至几周无响应，这样的计算效率显然远远不能满足实际应用需求。

折射静校正计算过程需共炮初至、共检初至及共中心点初至，以前做法是由共炮初至文件生成共检初至文件和共中心点初至文件，这样一个文件变成三个文件，大量地占用了磁盘空间，而且使用时要读入内存，初至文件稍大就有可能导致系统崩溃。为此，针对算法的需要重新设计了初至存储格式和初至数据管理方法：

(1)初至文件共炮结构存储；

(2)初至文件内容在原格式(图5a)基础上做了精简，只保留炮检索引和初至时间两列数据，炮点索引及初至位置作为辅助文件(图5b)；

(3)共检初至及共中心点初至采用一项专利技术[21]，高效快捷实时组织，磁盘空间和内存的使用降低4倍以上。

炮索引文件位置00120962409637890︙︙炮索引检索引炮检距初至00151.9104.101167.1114.502194.8123.903229.8146.3︙︙︙︙

(a)

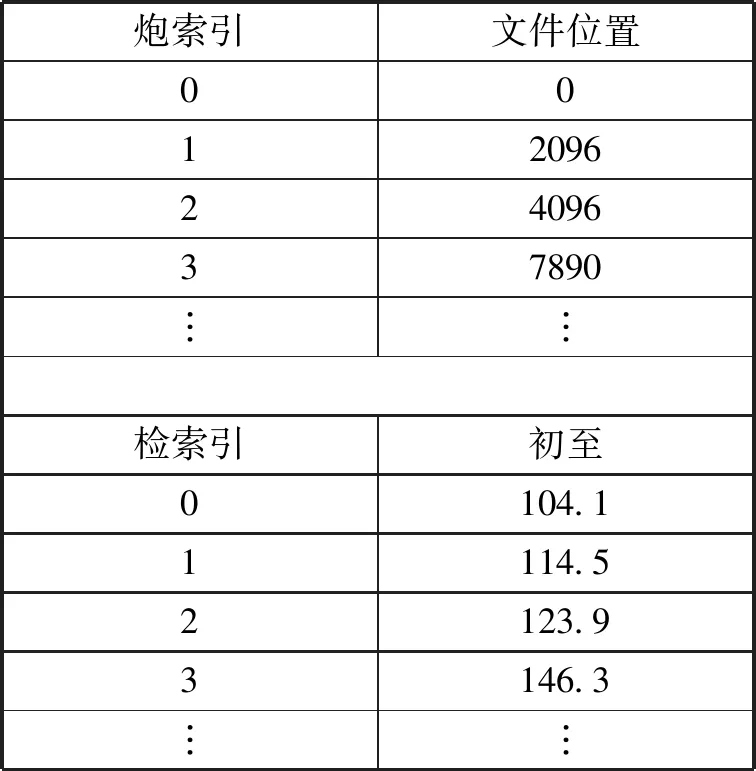
炮索引文件位置00120962409637890︙︙检索引初至0104.11114.52123.93146.3︙︙

(b)

图5 共炮初至文件格式

(a)原初至格式；(b)改进后初至格式

某工区40658炮，初至432502582道，表1中显示改进前后保存初至所需时间及占用磁盘空间对比情况。

表1 改进前、后性能提升对比表

初至文件格式的改进，使初至存取的效率大幅提高，存储空间大幅降低，也为折射层位划分、折射速度计算、延迟时计算的效率提升奠定基础。

2.2 高效的折射速度实现方法

折射速度的计算效率一直是折射静校正的一个瓶颈问题。常规的折射速度算法是根据两炮共用的检波点，然后按照折射速度计算原理求取折射速度，查找运算量随着数据量的增大呈几何级数增长，这是折射速度计算效率低的根本原因。为了提高折射速度计算效率，进行了各种实验(如按物理剩余内存批量读取初至，分批计算等)，但效率提升有限，效果都不理想。若要大幅提高折射速度计算效率，必须对原实现方法进行彻底改进。

计算折射速度，最关键、最耗时的步骤就是查找两炮的共用检波点，所以针对查找量大、查找效率低的问题，提出了一种孔径约束折射速度计算方法。具体实施方法如下：

(1)对炮点进行分区，按照工区方位角划分为若干规则矩形网格，对网格进行顺序编号，并记录每个网格内的炮点；

(2)根据折射分层炮检距范围确定矩形网格编号范围，继而快速寻找所需炮点，此即“孔径约束法”；

(3)只查找炮检距范围内网格的共用检波点；

(4)根据折射速度计算原理求取折射速度。

计算过程中，矩形网格作为计算单元，从第一炮所在的网格开始，再根据折射分层的炮检距范围，确定第二炮的网格范围(图6)，此范围内每一个炮点依次作为第二炮，查找两炮的共用检波点初至，最后计算折射速度。

通过孔径约束(对于图6箭头网格内所有炮点，根据折射分层的炮检距范围画出两个半圆，只查找两个弧形区域网格内炮点，这样直接找出所需炮点，既保证了运算精度又极大地减小了查找运算量)，快速确定具有共同折射速度的炮检点分组，突破了逐点循环计算分组数据的常规做法的限制，同时采用了并行算法、共用检波点快速查找算法等多项技术，大幅度地提高了折射速度计算效率。大量实际数据测试表明，数据量越大，该方法优势越明显。

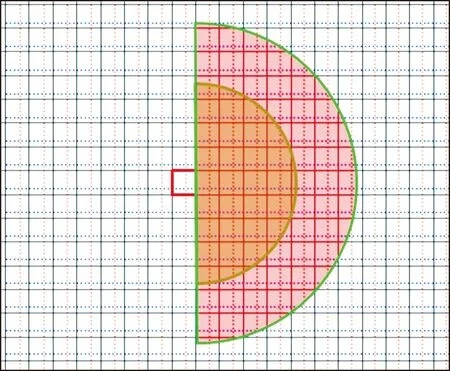
图6 孔径约束折射速度计算示意图

2.3 高效的延迟时计算方法

以往计算延迟时需在内存中读入共炮初至和共检初至，通过共炮初至计算炮点延迟时，通过共检初至计算检波点延迟时，迭代一次延迟时就需读两遍初至(共炮初至、共检初至各一次)，这是计算延迟时效率低的根本原因。从式(6)可看出，炮检点的延迟时是从剔除滑行时间的每一道初至上分解得到的，与共炮初至或共检初至没有直接联系，所以迭代一次延迟时需要读入两次初至完全是算法不合理造成的。通过对延迟时计算方法的深入剖析，实现了通过读入共炮初至，迭代一次、同时统计出炮点延迟时和检波点延迟时的计算方法。仅此一项改进，延迟时的计算时间就减少一半，再加上初至提取效率的提升对延迟时计算效率的影响，新算法延迟时的计算效率提升一倍以上。

3 理论模型试算

为了验证折射静校正算法的正确性，设计了一个地表起伏、界面水平的三维理论模型(图7)。模型参数分别设定为： 表层速度1000m/s，折射层速度2000m/s，地表高程2931.8～3204.7m，界面高程2920.0m。先后用本文折射方法(KLSeisⅡ)及某商用软件的折射静校正模块进行了计算，计算得到的折射层速度都比较准确，接近2000m/s，误差都在±0.1m/s之内(图8a)，但本文折射方法误差更小；而本文算法的延迟时误差明显小于商用软件(图8b)。

图7 理论模型

图8 KLSeisⅡ与某商用软件对比(针对一条检波线)

4 应用实例

将改进的折射法静校正技术应用于实际地震勘探，以检测其处理效果。图9a为中国西部M工区应用某商用软件折射静校正后叠加剖面，图9b为应用本文折射法静校正后叠加剖面，可看出本文折射方法静校正效果(右上方框)优于该商用软件。

图10a为N工区未做静校正的十字排列1500ms切片；图10b是应用某商用软件折射静校正切片；图10c是应用本文折射法静校正切片，其同相轴更接近同心圆，基本消除了静校正造成的同相轴扭曲，静校正效果优于商用软件。

对于软件的计算效率也做了大量的实际数据对比，选取了4个工区的数据，分别统计了某商用软件和本文方法求取折射速度的耗时及延迟时情况(表2)。针对表2中工区4的大数据，商用软件一周内未能计算出结果。在硬件及所用数据量相同条件下本文方法的效率是某商用软件的200～360倍。

图9 折射静校正后叠加剖面对比

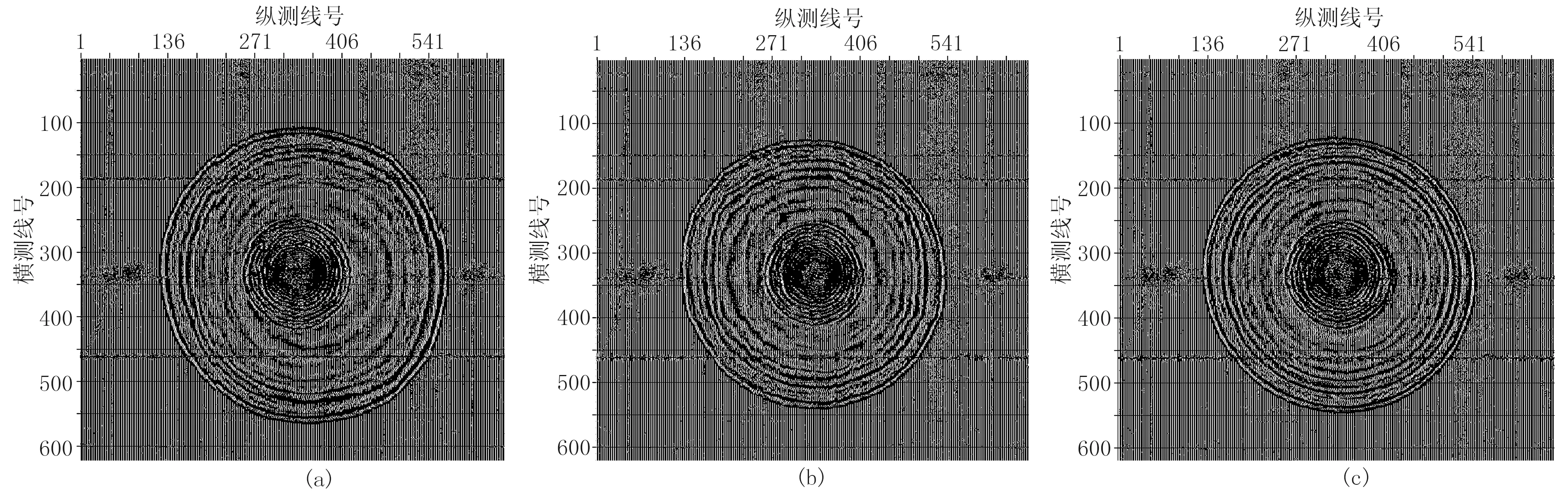
图10 十字排列1500ms切片对比

工区炮数电脑核数本文方法耗时商用软件耗时折射速度延迟时折射速度延迟时工区1 3617435s39s4h26min9min25s工区23524043min1min30s16h38min1h31min工区3755183min1min22h2h工区419601485min15s2min10s--

5 结论

针对折射静校正计算中初至文件占用内存大、提取效率低的问题，改进了初至文件的存取格式，采用随用随取的方式实现了高效的初至提取，为后续的高效折射速度计算及延迟时计算奠定基础；针对折射速度计算量大、计算效率低的问题，提出了一种孔径约束折射速度计算方法，明显提高了折射速度的计算效率；针对延迟时计算迭代一次需要读入两遍初至的问题，改进了实现算法，减少了每次迭代读入初至的次数，使得延迟时的计算效率提高一倍。这三项改进，为高密度地震勘探的现场处理奠定了基础。从实际应用的情况来看，本文折射静校正算法在保证了应用效果的同时计算效率远优于同类商用软件。