仿生算法优化BP神经网络在降雨空间插值中的应用

王汉涛， 张潇潇

(1.中国长江三峡集团有限公司， 湖北 宜昌443002；2.三峡水利枢纽梯级调度通信中心，四川 成都 610042； 3.四川大学 水利水电学院， 四川 成都 610065)

1 研究背景

降雨是影响流域水循环最活跃的因素，对流域产汇流的形成起着决定性的作用。降雨空间插值研究有利于掌握降雨的空间分布特征，对区域水文水情分析、水资源管理、旱涝灾害预报等具有重要意义[1-2]。人工神经网络能通过对训练样本的学习有效地揭示变量间的非线性关系，并具备对未知样点的预测能力，因此，国内外学者将人工神经网络方法应用于降雨空间插值研究中。目前，人工神经网络在降雨空间插值中的研究主要集中在以下两个方面：一是直接采用人工神经网络(如BP神经网络、RBF神经网络等)对降雨量的空间分布进行模拟及预测[3-6]；二是将人工神经网络与普通克里金、反距离权重等传统插值方法相结合得到一种新的混合插值法[7-8]。本文直接采用BP神经网络构建降雨空间插值模型，用于三峡区间流域年、月、日降雨量空间插值计算中。

仿生算法是基于自然界生物种群的特殊行为方式提出的群体智能优化算法，同时具有全局和局部搜索能力，能快速收敛到全局最优解附近，适用于求解高维的复杂非线性优化问题[9]。仿生算法优化神经网络，主要解决神经网络初始连接权值和阈值难以确定的问题，目前在水文、气象等领域都有大量研究成果，广泛应用于时间序列预测中[10-15]，但是运用在空间插值领域较少。本文采用遗传、粒子群、蚁群3种仿生算法来优化求解BP神经网络的初始连接权值和阈值，并构建了相应的降雨空间插值模型，以期提高BP模型插值的稳定性和精度。将插值结果分别与泰森多边形(Thiessen Polygon, TP)、反距离加权(Inverse Distance Weighted, IDW)和普通克里金法(Ordinary Kriging , OK)3种常规插值方法进行对比。

2 研究流域及数据

2.1 研究流域

以长江干流寸滩水文站和支流乌江武隆水文站到三峡大坝之间的三峡区间流域为研究对象。三峡区间流域集水面积约为6×104km2，干流全长658 km，位于东经106°36′00″～110°44′00″，北纬28°56′00″～31°44′18″之间。区内地形地貌条件复杂，支流水系均较短小。

三峡区间属北温带与亚热带季风气候的过渡带，受峡谷地形影响，其气候要素东西差异大，具有多雨、多雾、湿润、冬暖夏热等特点。暴雨发生频繁、降雨强度大，暴雨走向多为自西向东、沿干流向下游移动[16]。

2.2 研究数据

研究流域雨量数据由三峡集团水雨情遥测系统提供。共计99个站点，随机选取89个站点作为插值训练站，10个站点作为测试站，10个测试站分别位于不同的子流域，站点分布见图1。

以研究区内2014年降雨量、2014年8月降雨量、2014年8月31日降雨量作为年、月、日降雨量空间插值对象。

图1 研究区雨量站点空间分布

2.3 降雨量影响因子选择

地理位置、地形特征是影响降雨空间分布的重要因素，本文初步选择经度、纬度、高程、坡度和坡向等因子作为降雨影响因子[17]。将各影响因子与降雨量进行相关性分析，见表1。结果显示，纬度与降雨量相关性最好、经度次之、其余因子相关性较差，因此，本文最终选择经度、纬度作为三峡区间降雨量的主要影响因子。

表1 降雨量与各影响因子的相关系数

注：*表示在 0.05 水平(双侧)上显著相关，**表示在0.01 水平(双侧)上显著相关。

3 研究方法

3.1 单纯BP神经网络模型

BP神经网络(Back Propagation Neural Network, 简称BP)是一种多层前馈神经网络，通过信号正向传播和误差反向传播不断调整连接权值、阈值，使预测输出不断逼近期望输出。正反两个阶段反复交替，直到网络收敛为止[18]。

本次研究以降雨量的影响因子(经度、纬度)作为输入层变量、神经元数为2，降雨量作为输出层变量、神经元数为1，构建BP神经网络。隐含层神经元数在经验公式确定的范围内选取[19-20]。随机生成输入层与隐含层、隐含层与输出层神经元之间的初始连接权值，隐含层、输出层神经元初始阈值。

通过对BP神经网络进行训练，能够逼近降雨量影响因子和降雨量之间的非线性函数关系，实现降雨空间插值。但是，BP神经网络对初始权阈值依赖较大，在训练过程中，初始连接权阈值的选取是随机生成的、具有很大的不确定性，若设置不合理，会出现收敛速度变慢或者陷入局部最优的情况，也可能会出现震荡、不收敛的情况；此外，由于BP神经网络结构、参数设置的任意性，也会导致训练过程中出现过拟合现象。

3.2 仿生算法优化BP神经网络模型

仿生算法是基于自然界生物种群的特殊行为方式提出的群体智能优化算法，同时具有全局和局部搜索能力，能快速收敛到全局最优解附近，适用于求解高维的复杂非线性优化问题[9]。本文采用遗传(Genetic Algorithm，GA)、粒子群(Particle Swarm Optimization，PSO)[21]、蚁群(Ant Colony Optimization，ACO)3种仿生算法来优化求解BP神经网络的初始连接权值和阈值，分别构建了GABP、PSOBP、ACOBP模型，以降低BP神经网络在训练过程中陷入局部最小、过拟合的风险，提高降雨空间插值预测稳定性和精度；选择绝对误差和作为适应度函数。计算流程如图2所示。

图2 仿生算法优化BP神经网络流程

遗传算法(Genetic Algorithms, GA)实现过程中对染色体数量、交叉概率、变异概率、迭代次数等参数进行了调节；粒子群算法(Particle Swarm Optimization, PSO)实现过程中对粒子群数量、飞行速度限制范围、迭代次数等参数进行了调节；蚁群算法(Ant Colony Optimization, ACO)实现过程中对蚁群数量、迭代次数等参数进行了调节。

3.3 误差评价指标

本次研究采用均方根误差和判定系数两个指标对测试站降雨量模拟精度进行评价。

等把吉尔金娜那些年轻的朋友送走之后，江大亮的酒劲也上来了，就有些难以自持，那些客人刚走，吉尔金娜就迫不急待地捧起江大亮的脸就亲吻起来，吉尔金娜很狂热，用力将江大亮推倒在床上奋不顾身地用那隆起的双乳挤压在江大亮铁铜色的胸上，江大亮终于被吉尔金娜火热的激情给烤化了，就跟吉尔金娜默契地配合着，运作着，两个人似乎都投入到无比的幸福之中。

(1)均方根误差。均方根误差RMSE越小，表明预测值越接近实测值，预测的精度越高，见公式(1)。

(1)

(2)判定系数。判定系数R2越接近1，表明模型对数据拟合得越好，见公式(2)。

(2)

4 结果分析与讨论

4.1 结果分析

算法参数的设置对解的质量有着非常重要的影响，因此需要对相关参数进行反复调试。选取4种BP模型在年、月、日降雨量空间插值中RMSE值表现最优、最差的参数组合，列于表2。4种BP模型和3种常规插值方法得到的降雨量预测误差指标RMSE统计及预测结果分别见表3、图3～5。

对3种常用插值方法得到的RMSE进行比较：从图3～5可以看出，2014年、2014年8月降雨量OK方法插值效果较好，2014年8月31日降雨量IDW方法插值效果较好，TP方法整体误差较大。从表3可以看出，TP方法训练集RMSE值为0，IDW方法训练集RMSE值近似为0，体现了精确性插值方法的特点；OK方法训练集RMSE值较大，符合其本身为非精确性插值方法的情况。

对BP模型得到的测试集RMSE与训练集RMSE进行比较发现(表3)：单纯BP模型得到的测试集RMSE整体上大于训练集RMSE，存在过拟合的可能。有学者认为，网络学习过多是导致过拟合问题发生的重要原因[22-24]；本文将BP训练步数设置为500、1000、1500、2000、2500、3000共6种情形，均没有获得较好的推广能力。因此，笔者认为，相比起训练步数，BP的网络结构设置和模型参数选取对训练结果影响更大。通过仿生算法对BP神经网络初始权值和阈值进行优化，可以降低网络过度拟合的风险，GABP、PSOBP、ACOBP模型较BP预测能力均有较大的提高。

对BP模型和仿生算法优化后的BP模型得到的测试集RMSE进行比较(表3)：GA、PSO、ACO算法优化BP模型后，调试参数过程中出现的RMSE最大值有大幅度的下降，RMSE平均值整体减小；2014年降雨量RMSE最小值由PSOBP模型获得，但2014年8月、2014年8月31日降雨量RMSE最小值仍由BP模型获得。因此，仿生算法优化BP神经网络能够从整体上提高BP神经网络的预测精度和稳定性；但BP神经网络本身的学习特点决定了它在训练和模拟过程中存在较强的随机性，不能保证采用仿生算法对BP神经网络初始权值和阈值进行求解后一定会获得最好的插值结果。

对3种仿生算法优化后的BP模型得到的测试集RMSE进行比较(表3)：2014年降雨量RMSE最小值由PSOBP模型获得、最大值由GABP模型获得，2014年8月降雨量RMSE最小值由ACOBP模型获得、最大值由PSOBP模型获得，2014年8月31日降雨量RMSE最小值、最大值均由PSOBP模型获得。3种算法虽然原理、参数各不相同，但优化BP模型表现相当，没有明显的优劣之分。

对年、月、日插值结果进行比较：从图3～5可以看出，3种常用插值方法对日降雨量的拟合程度较好，月降雨量的拟合程度次之，年降雨量的拟合程度较差。4种BP模型通过调试参数，日降雨量拟合效果与3种常用插值方法相当，月、年降雨量均优于3种常用插值方法的效果；但BP模型稳定性欠佳，GABP、PSOBP、ACOBP模型整体表现较好。

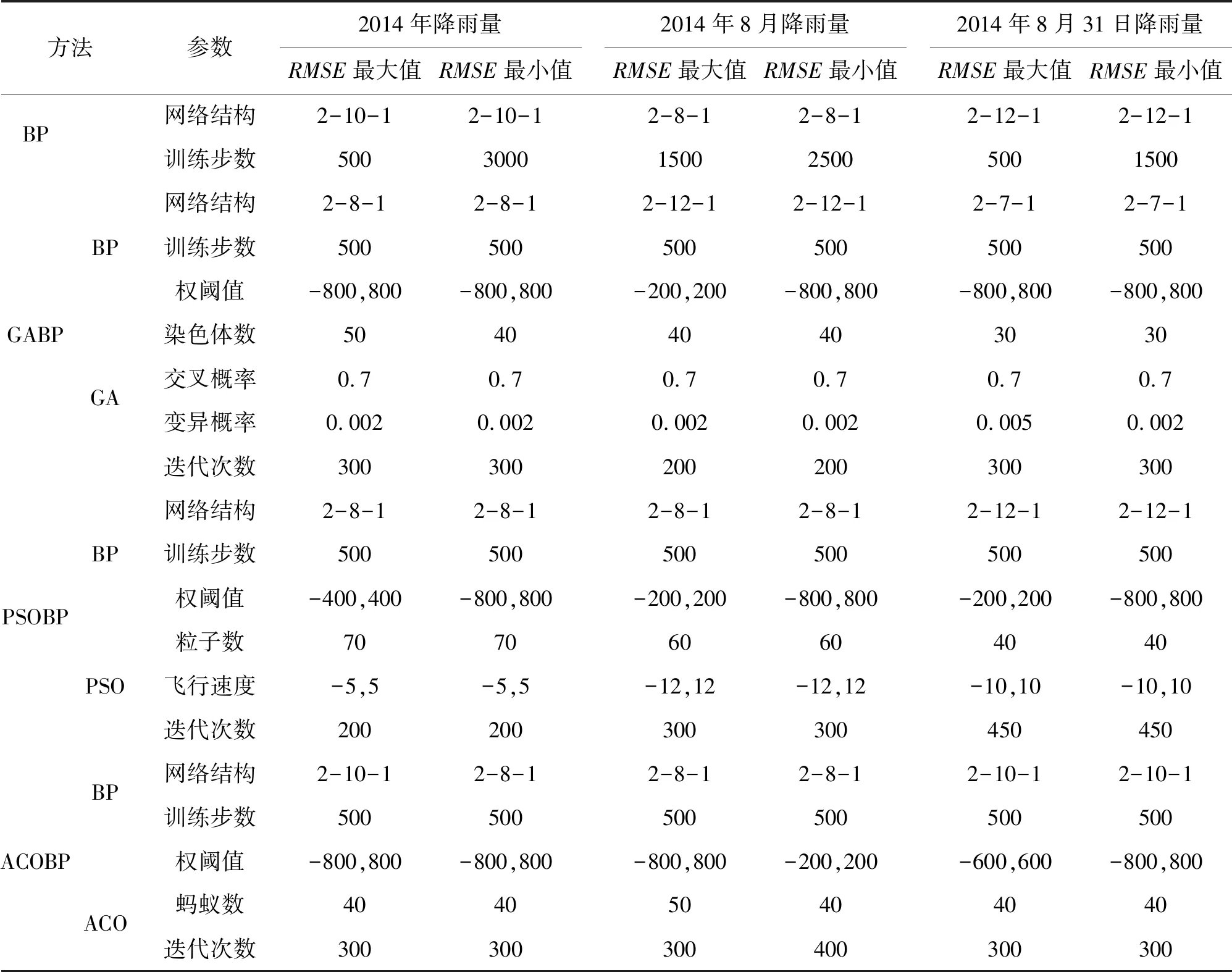
表2 4种BP模型在降雨量空间插值中RMSE值表现最优和最差的参数组合

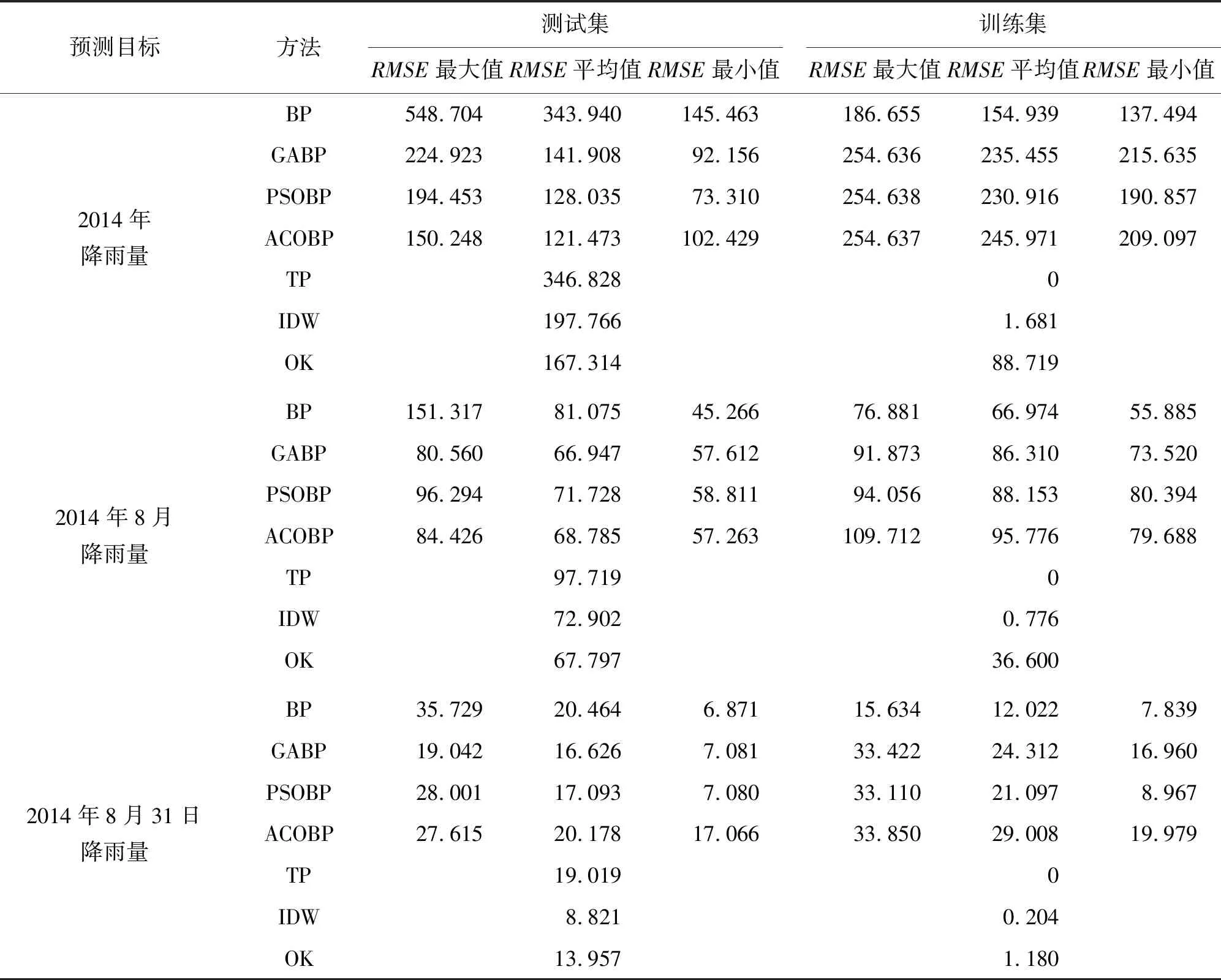
表3 4种BP模型和3种常规插值方法预测误差指标RMSE统计 mm

4.2 讨 论

整体来看，通过调试参数，仿生算法优化BP神经网络模型能够获得较好的降雨插值模拟和预测结果，若要将模型运用在长时间序列降雨量空间插值计算中，会面临以下两个问题：

(1)BP神经网络计算时间较短、通常1 min能完成一次计算(训练步数设置为3000)，但预测效果不稳定；采用仿生算法优化BP神经网络能够达到稳定的插值结果，但计算时间较长，不管是遗传、粒子群还是蚁群，通常要2 h才能完成一次计算(算法迭代次数设置为300，BP神经网络训练步数设置为500；计算机采用Intel(R)Core(TM)i3-2310M/CPU@2.10GHz处理器，内存为4.00GB，32位操作系统)。究其原因，一是仿生算法本身的参数设置具有一定的随机性、影响算法的收敛性能，冗余迭代使求得精确解的效率低；二是计算机性能不高。整体来看，仿生算法优化BP神经网络模型的时效性需要改良。

(2)仿生算法的参数设置对最终插值结果有较大程度的影响，而降雨量具有较强的时空分布特性，每个地区、每个时间段的降雨量都不会完全相同，因此需要根据每组数据分别进行参数调试，工作量大且受主观经验、判断制约，仿生算法优化BP神经网络模型的通用性有待进一步加强。

此外，在降雨量影响因子识别过程中，本文虽然考虑了三峡区间流域高程、坡度、坡向等影响因素，但是根据相关性分析，最终仅选择经度、纬度作为输入变量，降雨量作为输出变量，建立BP神经网络降雨插值模型。降雨量受多种因素影响，除了代表地理位置的经纬度，地形和气候带特征亦不容忽视，在接下来的研究工作中，有待进一步掌握三峡区间地形地貌特点和降雨形成机理，更好地挖掘影响三峡区间降雨量的特征因子；其次，区域的卫星降水数据与地面实测降雨有很好的相关性，下一步尝试将卫星降水数据作为辅助变量，提高地面站点降雨空间插值精度[25]；同时，考虑采用模糊熵聚类分析算法，对流域内雨量站进行模糊熵聚类研究，探索区间降雨的地理位置聚拢性，更好地进行降雨量空间插值研究[26]。

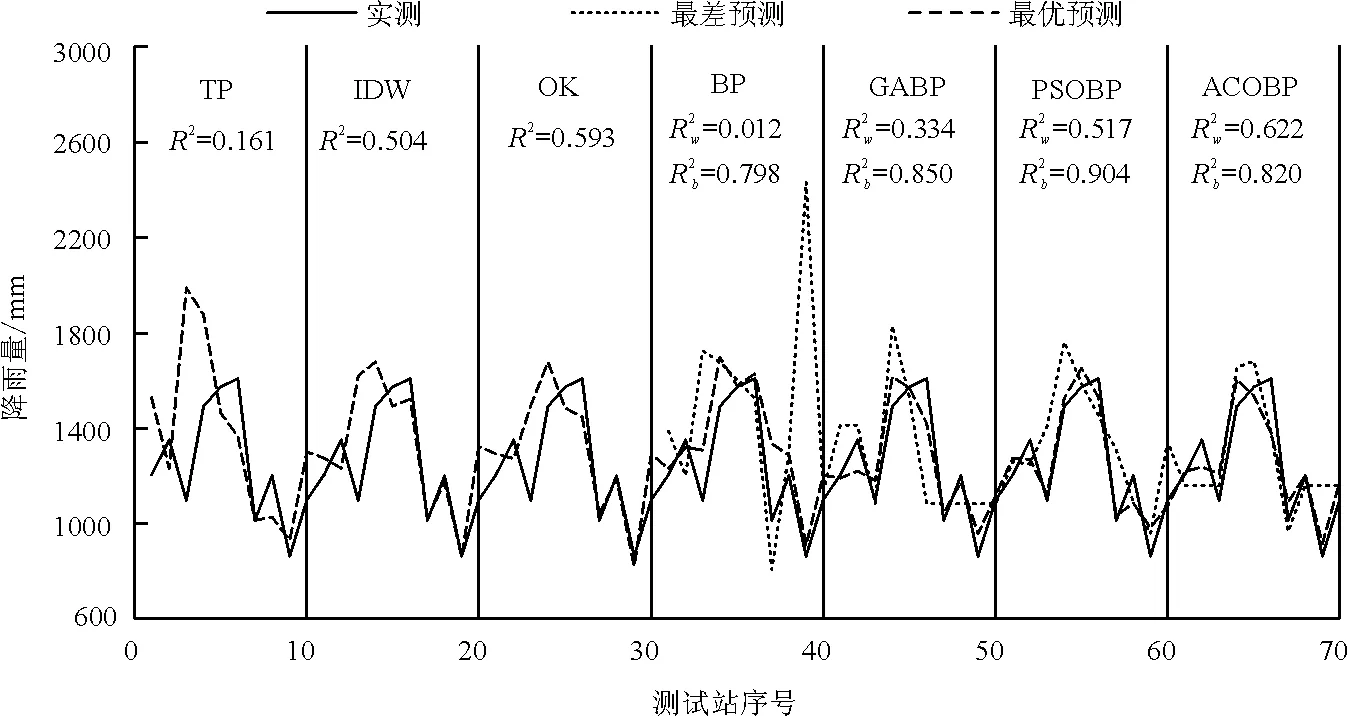
图3 测试站2014年降雨量插值结果

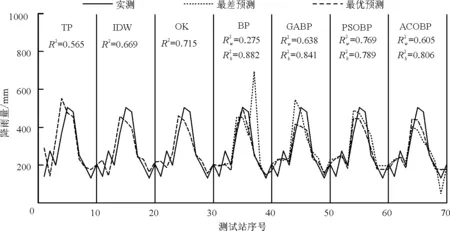
图4 测试站2014年8月降雨量插值结果

图5 测试站2014年8月31日降雨量插值结果

5 结 论

(1)较传统插值方法而言，BP神经网络能在一定程度上描述地理特征与降雨量的复杂非线性关系，但预测稳定性较差。

(2)选用遗传、粒子群、蚁群算法对BP神经网络的初始连接权值和阈值同时进行全局和局部搜索，不再采用随机生成的初始权阈值，降低了BP神经网络陷入局部最优、过度拟合的风险，GABP、PSOBP、ACOBP模型较BP预测能力均有较大的提高，可以在降雨空间插值领域进行更深入地研究和推广。

经仿生算法优化后的BP神经网络在三峡区间流域年、月、日尺度降雨量空间插值计算中，取得了理想的插值结果；但BP神经网络的拓扑结构、学习特点和仿生算法本身的参数设置均具有一定的随机性，仿生算法优化BP神经网络模型的时效性、通用性有待进一步改良。