基于含砂液流振动信号特征分析的出砂监测实验研究

王 锴， 刘 刚， 李祎宸， 王 刚， 冯 凯

(中国石油大学(华东) 石油工程学院，山东 青岛 266580)

液-固两相流广泛存在于石油工业，在原油开采的过程中，岩石层的细小砂粒伴随生产的液流进入生产管道[1]，造成管道冲蚀和阻塞，为安全生产埋下重大隐患[2-3]。油井生产过程中，准确预测和监测油井出砂，并将其可能造成的危害减少到最低，已成为迫切需要解决的关键问题。国内对出砂预测理论和技术有了较全面的研究，但出砂监测技术尚属起步阶段[4-5]。同时由于液-固两相流动的复杂性，多相流中的固相测量在国际上还未得到满意的解决，而成为是国内外研究人员探索的热点课题[6-9]。

近年来一些学者对多相流中的固相检测展开研究，Xu等[10]基于静电测量原理对气-砂两相流中的砂粒速度和粒径特性进行了研究；Hii等[11]基于声发射原理成功获得了气-固两相流中固相含量特性；El-alej等[12]利用声发射技术获得了水-砂两相流中砂含量特性；而基于振动信号时-频特征分析的水-砂两相流中砂粒监测研究还未见大量报道。液-固两相流动冲击管壁激发的是非平稳随机信号，而目前针对非平稳随机信号没有统一完整的描述方法，为实现液-固两相流中砂粒相检测，必须对含砂液流激发的振动信号进行时-频特征分析。Ong等[13]基于小波变换构造阈值函数对流体激发的噪声进行表征，但是很难构造匹配流体特征的小波基；Aghdam等[14]基于ARMA时序模型对非平稳振动信号特征提取，但存在建模复杂、阶数选取和计算量之间矛盾等问题； Liu[15]基于WVD分布获得能量集中性最优的时-频表示，但是在分析多分量信号时会受到交叉项的干扰。因此有必要进一步研究适用于基于含砂液流时-频特征分析的油井出砂监测方法。

本文针对高含水期油田出砂问题，提出了一种利用加速度计、采集仪获取管壁振动信号，并通过分析水-砂两相流流动冲击管壁激励振动信号时-频特征，监测出砂量变化的方法。该方法与上述提到的其他检测方法相比，具有安装方便、实时监测、体积较小和成本低等明显优势。同时该方法也可为生产单位及时调整生产参数，以降低和避免过度出砂对生产设备损坏、对提高油田生产效率，降低生产成本意义重大。

1 水-砂两相流中砂粒监测原理

水-砂两相流在管路流动时具有一定动能，当携砂流体以较高速度流经管道90°弯头处时，由于流体流向突变，砂粒会在惯性的作用下摆脱液流拖拽力的束缚而冲击到管壁上并产生振动，如图1所示。

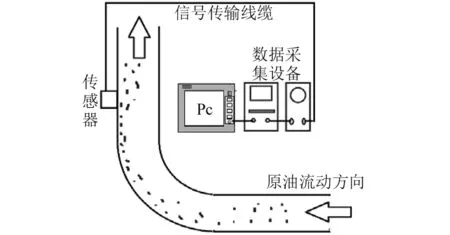
图1 水-砂两相流中砂粒监测示意图Fig.1 The schematic diagram of sand monitor in sand-water two-phase flow

砂粒对管壁做功产生一定的冲击动能，弯头外侧的传感器拾取该振动特征，并进一步转化为所需的砂粒参数，其中砂粒产生的动能KE为[16]

(1)

式中：m为砂粒的质量；v为颗粒冲击管壁的速度，可以看出砂粒的动能随含砂量或者流速的增加而增加。

重质液流中的低含量砂粒冲击管壁激励的振动信号十分微弱，为了有效的区分砂粒与液流冲击管壁激励的信号频域特征，本文采用基于短时傅里叶变换(Short-Time Fourier Transform,STFT)的时-频分析方法对砂粒信号进行识别。STFT的原理是在时间轴上滑动固定宽度的时间窗，把信号分为多个等时段。在短时段信号内，认为信号平稳，利用傅里叶变换获得信号的谱信息，将所有时间段的频谱信息综合考虑，得到时间-频率分析的二维结果。这种方法将非平稳信号的一维时域分析转换为二维的时-频分析[17]，可以直接提供信号的广谱频率信号特征和相对应的能量特征，其能量幅值为

(2)

式中：h(t)是以t=0为中心的窗函数，其变换可以看出信号在正交基函数上的分解，短时傅里叶变换的基函数在不同的变换中同时具有时间和频率分辨率。

获得砂粒信号特征频段后，采用带通数字带通滤波的方法进一步滤除液流信号，提取砂粒信号，其传递函数为

(3)

式中：N为滤波阶数；M为传递函数的零点；a1k和b1k为权重函数系数。

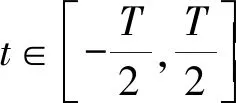
(4)

2 实验设计和监测方法

2.1 实验装置

实验平台如图2所示，可提供最大排量为12 m3/h，管壁最大耐压值为1.2 MPa，提供流态透明观察窗，具有温度、流速测量与控制单元；在距螺杆泵出口300倍管径处布置超声波流速测量装置，用以监测流体实时流速；在储液罐上布置温度测量与控制单元，用以监测并控制含砂油流温度；在螺杆泵出口200倍管径处布置压力传感器，用以监测系统压力变化；在管线下弯头2～3倍管径处,即砂粒以较高速度冲击管壁的位置[18]，布置一个加速度传感器以获取油流、含砂油流冲击管壁激发的一次信号；通过加速度计、电荷放大器和数据采集仪等振动信号检测装置获取室内实验条件下的油井出砂振动信号。

2.2 实验设计

实验砂样为石英砂，密度为2.65 g/cm3，莫氏硬度为7；实验温度为10摄氏度；设置不同流体流速、不同砂粒粒径、不同含砂量条件，开展室内出砂监测实验，具体流程如下：

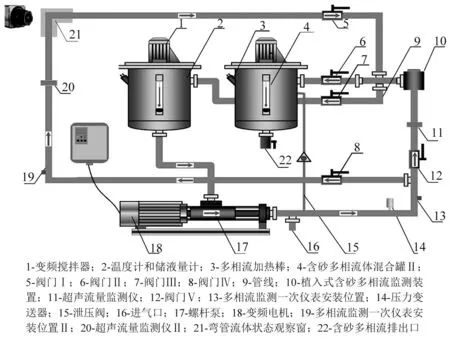
图2 多相流携砂流体室内模拟实验平台示意图Fig.2 The experimental step of sand-carrying multiphase flow in the lab

(1) 携砂液流的流速分别为2.5 m/s，3.0 m/s，3.5 m/s和4.0 m/s时设计室内出砂监测实验，以研究流体速度与监测信号之间的关系。

(2) 液流中砂粒的质量浓度分别为0%，0.06%，0.09%，0.12%和0.15%时设计室内出砂监测实验，以研究携砂流中砂粒与监测信号之间的关系。

(3) 砂粒粒径分别为80目、100目、150目、200目和325目时设计室内出砂监测实验，以研究不同携砂流中砂粒大小与监测信号之间的关系。

3 实验结果分析

本文采用STFT时-频分析方法对水-砂两相流冲击管壁激发的信号特征进行分析，其中单个时域信号时长164 ms，频率带宽为20 kHz，谱线数为400条，采用指数方法对信号进行平均处理，平均时间为20 ms，窗函数为汉明窗，信号重复率为66.7%，其中时-频分析结果中能量最高值的3%以内区域用白色实线圈出。

3.1 水-砂两相流流动特性

通过高速摄像法研究传感器安装位置附近的携砂体的流动特性，如图3所示为不同流速下的水-砂两相流流动特性。

多相流体速度为2.5 m/s时的流动特性如图3(a)所示，管路中的点状亮点为微量气泡，亮点的运动轨迹即为流体流动轨迹，管流中的微量气泡分布均匀，流动稳定。如图3(b)～图3(d)为不同流速下的流动特性，与2.5 m/s流速下的流动状况对比可知，在2.5～4.0 m/s流速下流动稳定，运动轨迹没有明显变化，且拍摄到的亮点运动轨迹线增长，与流速增长的实验条件相符。因此在实验条件下，流体运动特性没有发生明显变化，可以将2.5～4.0 m/s的流速条件作为水-砂两相流中固相检测的流体流动基本参数。

图3 不同流速下水-砂多相流流动特性Fig.3 The characteristics of sand-water flow in different velocity

3.2 不同流速下液流信号特征分析

基于STFT时-频分析研究液流在含砂前后激励振动信号特征的区别。如图4为不同流速下的分析结果，随着流体速度的增加信号幅值增加，时域信号具有微弱的冲击特征，液流冲击管壁产生的信号频率分布广泛，主要集中在3～10.0 kHz和12.5～14.0 kHz两个频段，且低频段信号强度较高。相对能量分析结果表明，随着流速的增加，流体冲击管壁产生的能量增加。

如图4(a)所示为2.5 m/s流速下的时-频分析结果，相对能量最高的频段主要集中在4.0～7.5 kHz,当时域信号具有明显冲击特征时，对应时段内的低频信号强度出现最大值，如0～30 ms，60～90 ms和125～150 ms在4.0～7.5 kHz频段内的信号特征。如图4(b)～图4(d)中3～4 m/s流体流速下的时-频分析结果均和2.5 m/s流速下的信号特征相似，且随着流速的增加12 kHz以上的高频段内信号相对能量强度增加。

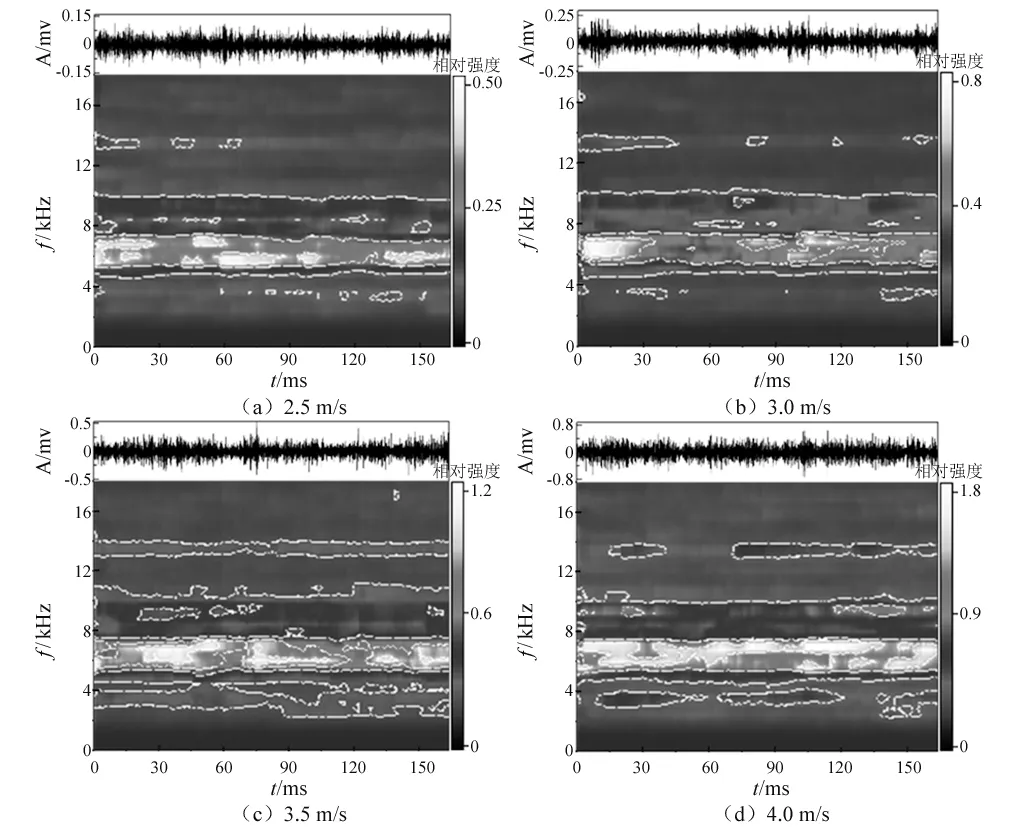
图4 不同流速下液流时-频分析结果Fig.4 The time-frequency results of water flow in different flow velocity

3.3 不同流速下水-砂多相流信号特征分析

水-砂两相流实验中选取的砂样粒径小、含量低、液流的携砂能力强，因此，砂粒与液流的相对滑移速度可忽略不计，即近似认为砂粒流动的速度等于液流流动的速度。当砂粒粒径为80目，质量分数为0.15%时，对不同流速下的含砂液流冲击管壁产生的振动信号进行时-频分析，以研究液流在含砂前后激发的信号特征区别。

如图5所示为2.5～4.0 m/s含砂液流振动信号时-频分析结果，时域分析结果表明随着液流流速的增加，信号幅值相应增加。频域分析结果表明携砂流体冲击管壁产生的振动信号集中在3～4 kHz，4.2～9.0 kHz，10～13 kHz和13～15 kHz 4个频段内，信号能量强度的高值主要集中在9 kHz以下的低频段。相对能量分析结果表明随着携砂液流的流速增加，传感器获得的振动信号强度增加。

与图4中无砂流体冲击管壁产生的振动信号特征对比可知，在10 kHz以下的频率分布特征基本一致，但是在10～15 kHz的高频段内，携砂流体冲击管壁产生相对能量较高的高频特性。由于无砂流体冲击管壁在12.5～14.0 kHz频段内也有频率响应，因此选取10.5～12.5 kHz为砂粒冲击管壁产生的特征频段。

如图5(a)所示为2.5 m/s流速下的时-频分析结果，当时域信号具有明显冲击特征时，高频和低频信号强度均出现高值，如20～45 ms时间段内的信号，即在弯头附近，流体流向突变，冲击管壁产生低频振动信号，同时流体中的砂粒在惯性的作用下摆脱流体的束缚力，冲击到弯头附近的管壁产生高频振动信号。如图5(b)～图5(d)中3.0～4.0 m/s流体流速下的时-频分析结果均和2.5 m/s流速下的信号特征相似，流体冲击管壁产生10 kHz以下的低频信号，同时在10.5～12.5 kHz内出现砂粒冲击管壁产生的高频信号，且随着流体流速的增加高频段内信号的相对能量强度增加。

图5 不同流速下水-砂多相流时-频分析结果Fig.5 The time-frequency results of sand-water flow in different flow velocity

3.4 水-砂两相流冲击管壁信号能量分析

基于水-砂两相流信号的时-频特征分析结果，对出砂特征频段(10.5～12.5 kHz)内的信号进行滤波降噪，得到水-砂多相流冲击管壁产生振动信号的相对平均振动能量，如图6所示。

图6 不同流速、不同目数下的砂粒冲击管壁信号能量Fig.6 The vibration energy of sand-water flow with different sand size and velocity

图6(b)～图6(e)中，砂粒目数分别为200目、150目、100目和80目的结果表明，携砂流流速一定的情况下，水-砂两相流冲击管壁产生的相对平均振动能量随着含砂量的增加而增加；在含砂量一定的情况下，水-砂两相流冲击管壁产生的相对平均振动能量随携砂流流速的增加而增加。

图6中，对比不同砂粒大小下的携砂流冲击管壁产生的振动能量可知，含砂量一定，水-砂两相流冲击管壁产生的相对振动平均能量随着砂粒大小的增加而增加；当携砂流流速一定，相对振动平均能量随着砂粒粒径的增加而增加。不同流速的水-砂两相流冲击管壁产生平均振动能量用三阶多项式[19]拟合表示，如下式Gwater(v)

Gwater(v)=b0+b1·v+b2·v2+b3·v3

(5)

图6中，含砂量为零时，不同流体流速下对应的振动平均能量代入式(5)中，即可得到三阶多项式拟合系数，见表1。

表1 式(5)中的系数

3.5 水-砂两相流中砂粒振动能量数学模型

3.5.1 水-砂两相流中砂粒振动能量验证

为了测试振动方法检测水-砂两相流中砂粒相的有效性，即验证特征砂频段内的流体信号降噪后的获取的砂粒信号，是否由砂粒冲击管壁引起。如图7(a)所示，将200目砂粒装入不同出口直径(D1=0.5 mm,D2=1.0 mm,D3=1.5 mm,D4=2.0 mm)的4个锥形漏斗中，漏斗出口距管路上壁面的垂直距离为20 cm。砂粒在重力的作用下分别以不同的砂量冲击到外管壁，同时水流在管路中以2.5 m/s流速流动，分别对不同砂量下的相对功率谱进行实时分析。

如图7(b)所示，实验结果表明在管内流体流速一定，随着砂量的增加，相对功率谱幅值增加，流体冲击管壁产生相对功率谱幅值未见明显波动。因此提取的砂粒冲击管壁的信号确实由砂粒冲击管壁引起，本文提到的振动检测方法有效。

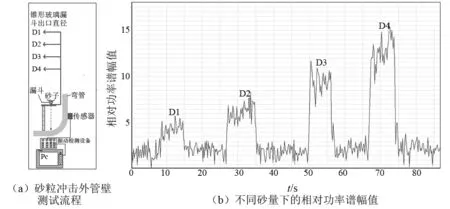
图7 砂粒冲击外管壁测试流程下的相对功率谱幅值Fig.7 The relative amplitude of power spectrum for sand impacting on the surface of pipeline

3.5.2 管外砂粒振动能量分析

为获得实时含砂率，设计砂粒以不同速度冲击外管壁校准实验，校准实验如图8所示，砂粒装入漏斗且与平板水平放置，使得砂粒以轴向方式冲击平板。即在重力的作用下，砂粒以自由落体的方式冲击平板，且平板的材质与管道的材质厚度相同。通过调节漏斗距离平板的高度控制砂砾冲击管壁的速度，设计漏斗出口直径确定砂流量率。实验设计砂粒自由落体的高度分别为32 cm，46 cm，63 cm，82 cm，忽略动能损失，砂粒冲击平板的速度分别为2.5 m/s，3.0 m/s，3.5 m/s，4.0 m/s；砂粒粒径分别为45 μm，75 μm，106 μm，150 μm，180 μm；砂粒质量流量率为1 g/s。

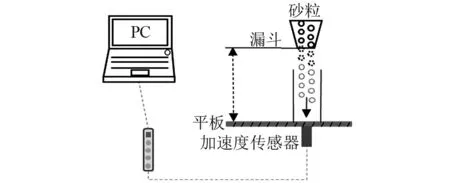
图8 校准实验示意图Fig.8 The schematic of calibration experiment

对砂粒冲击外管壁的信号进行10.5～12.5 kHz滤波，以校准水-砂两相流中的砂粒信号，如图9所示。结果表明随着砂粒粒径的增加，砂粒冲击管壁产生的振动能量增加，随着砂粒冲击管壁速度的增加，管壁处产生的振动能量增加。

图9 不同砂粒目数下的砂粒冲击管壁能量分析结果Fig.9 The vibration energy analysis results of sand impacting on the wall with different sand size

利用三阶多项式对2.5～4.0 m/s内获取的振动信号进行拟合，以获得砂粒冲击管壁的速度与相对平均振动能量的关系。记F(v)sand为砂粒冲击管壁产生的平均振动能量，则多项式拟合后的表达式为

F(v)sand|(1 g/s,f)=a0+a1·v+a2·v2+a3·v3

(6)

分别对应不同粒径砂粒，最终求得的拟合系数见图8右上角内表格。则表格内拟合系数与砂粒粒径的关系可以用以下线性方程组表示

(7)

式中：P为砂粒粒径，拟合系数与砂粒粒径关系中的系数见表2。

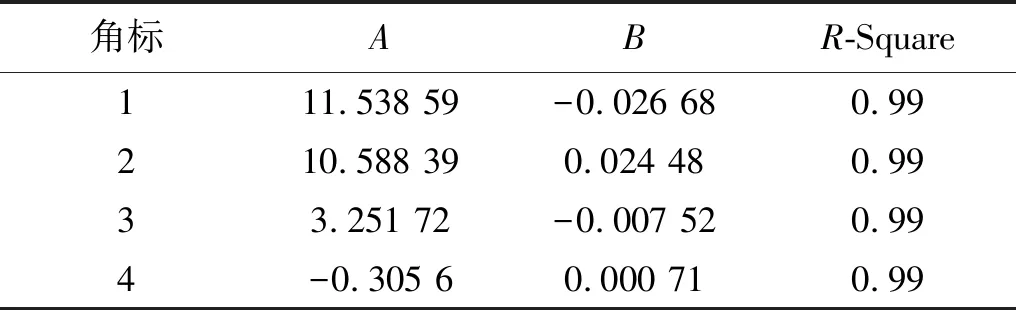
表2 式(7)中的系数

3.5.3 砂粒振动能量数学模型

水-砂两相流中砂粒信号的检测中，将含砂率作为检测效果评判标准。单一流速和含砂量下的水-砂两相流冲击管壁产生振动能量，对每秒内的信号进行积分，计算10 min内的600个积分的信号的平均振动能量。水-砂两相流冲击管壁产生的振动信号经过加速度传感器采集为电荷信号，经过电荷放大转换后变成电压信号，最后通过信号采集卡及相关信号处理模块转换为图6中的相对振动能量。该振动能量可以描述含砂率的趋势，但是为了进一步获得较为精确的含砂率，需对振动能量信号进行降噪量化处理。即水-砂两相流冲击管壁产生的振动信号幅值减去该实验条件下的水流冲击管壁产生的振动信号，实现水流信号的降噪。进一步定量分析含砂率，将经过信号降噪处理后的水-砂两相流信号除以参考校准砂信号，即1 g/s砂流量率下的砂粒冲击管壁产生的振动信号。为了增加砂流量率计算的准确性，引入线性校准系数A和指数校准系数B，含砂率计算公式如式(8)所示

(8)

进一步验证含砂率计算公式的准确性，利用该公式对不同流速下水-砂两相流冲击管壁信号进行计算，其中砂粒粒径大小为200目，每个流速实验次数为4。如图10所示为含砂率计算后得到的含砂率，结果表明采用该算法可以将不同的流体流速条件下对含砂量的影响弱化，且计算误差在14%以内，因此采用振动方法可以对水-砂两相流中的含砂量进行定量检测。

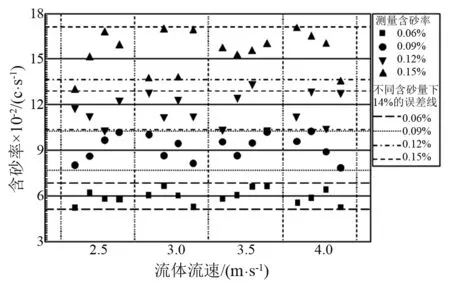
图10 含砂率计算结果Fig.10 The sand content calculated result

4 结 论

本文采用振动方法对基于水-砂多相流流动的管线出砂监测展开实验研究。通过设计室内出砂实验，对不同流体速度、不同含砂量、不同砂粒粒径下的水-砂两相流信号STFT时-频特征进行分析，结果表明水-砂两相流中的出砂信号特征频段为10.5～12.5 kHz，且随着砂粒含砂量的增加，特征频段内的相对平均振动能量幅值相应增加。进一步通过设计校准实验，定量分析了水-砂多相流中砂粒含量，并建立了数学模型，误差分析结果表明含砂率与系统提供含砂率误差在14%范围内，因此本文提出的振动监测方法对该方法为更复杂多相流出砂监测研究奠定了基础，为油井安全生产提供了技术保障。