基于梯形直觉模糊集的复杂产品模块划分*

王保兴，刘 丹，周同新，黄海涛

(贵州大学 现代制造技术教育部重点实验室，贵阳 550025)

0 引言

模块化设计作为一种先进的设计方法，主要是通过对通用模块的选择与组合实现对客户定制产品的快速设计。作为模块化设计的前提与基础，合理的模块划分能够有效降低产品的生命周期、缩短产品的开发时间以及充分考虑客户的定制要求，并为面向大规模定制的模块化设计提供有效的保障[1]。

目前国内外许多学者针对模块划分技术与方法进行了相关的研究，谌炎辉等[2]对目前已有的模块划分方法进行了归纳与总结，提出现有的模块划分角度有基于功能的、基于结构的、基于生命周期的。复杂产品具有零部件数目繁多、结构复杂和零部件关联关系错综复杂的特点，将现有的模块划分方法应用到复杂产品时，会造成计算量大及划分过程复杂化的问题。

近年来，考虑到复杂网络理论的社团结构思想与复杂产品模块理念的相似性，有学者提出将复杂网络的社团结构发现方法应用于产品模块划分。樊蓓蓓等[3]提出使用复杂网络理论对产品的结构进行建模，并定义网络的节点为产品的零部件，网络的边抽象为零部件之间的关联关系，但在边权的确定中，采用的是父节点包含的子节点的数目，这种方法不能有效的描述节点间的关联关系。杨格兰[4]同样将复杂网络的GN算法应用于产品的模块划分中，但是在定义产品结构的关联关系时，采用0和1表示方法，即1表示结构单元间有关联，0表示无关联，这种表示方式没有充分考虑到节点间的具体关联度，会造成划分结果不精确。李玉鹏[5]将复杂网络应用于产品的模块划分时，分析了零部件之间的功能、结构相关性，并给出功能与结构的量化准则，但是在确定复杂网络的边权时，由于设计者的经验及专业化水平的影响，容易导致主观的不确定性。

为解决复杂产品的模块划分问题，本文提出将加权复杂网络理论应用于复杂产品模块划分中，为减少模块划分及边权确定过程中存在的模糊性与不确定性，将模糊集理论引入到模块划分的多属性决策问题中；并研究了关于产品的结构、功能及客户参与度的关联关系定量化方法，采用基于梯形直觉模糊数理论计算加权复杂网络的边权；对产品的结构、功能及客户参与进行相关性分析，得出各自的相关性矩阵及综合先关矩阵，最后通过复杂网络算法实现产品的模块划分。

1 基于复杂网络的产品模块划分

1.1 零部件间边权的赋权

利用加权复杂网络解决复杂产品的模块划分时，网络边权的确定是划分的基础与前提。对于复杂机械产品的模块划分来说，描述零部件之间关系时由于设计者的经验及专业化水平的不同，容易导致复杂产品零部件边权赋值时存在大量的主观的不确定性。为减少这种主观不确定性与模糊性，贾凡[6]为有效表述信息的不确定性，引入模糊数与粗糙数的理论，并将决策者的主观信息转化成模糊数与粗糙数，从而实现信息的有效集结；Zhang Na[7]利用区间值直觉模糊集来确定各零部件之间的关系，提出一种新的区间直觉模糊数精确度函数，以完成边权的赋值；V Lakshmana Gomathi Nayagam[8]也提出一种新的基于梯形直觉模糊数的多属性群决策方法，有效实现不确定信息环境下模糊多属性决策问题的解决。

为减少复杂产品零部件边权赋值过程中存在的模糊性，本文采用基于梯形直觉模糊数理论计算加权复杂网络的边权，利用梯形直觉模糊数的打分函数实现边权的打分赋值。给出关于梯形直觉模糊数的基本定义。

设M=〈(a1,a2,a3,a4),(a1′,a2′,a3′,a4′),ωM,uM〉是实数集R上的直觉模糊集，ωM，μM为隶属度与非隶属度，定义梯形直觉模糊集的(value index)与(ambiguity index)为：

IV(M,λ)=IVu(M)+λ(IVv(M)-IVu(M) )

(1)

IA(M,λ)=IVv(M)-λ(IVv(M)-IVu(M) )

(2)

λ[0,1]代表决策者的偏好信息，当λ[0,1/2] 时，表示决策者喜欢不确定或消极的感觉；λ[1/2,1]时，表示决策者喜欢确定性或积极的感觉；λ=1/2时，表示决策者对积极情绪或消极情绪不关心。

1.2 定性指标的定量化

通过矩阵的变换实现对零部件产品的相关性分析，但是对产品进行相关性分析时，考虑不同的因素，将会导致不同的划分结果。李玉鹏[5]在研究中考虑了零部件之间的功能、结构相关性，并给出功能与结构的量化准则，从而为复杂网络边的赋权提供基础。本文也是采用矩阵变换的方式实现复杂产品零部件的相关性分析，并将复杂产品的结构、功能及客户参与度作为量化指标，实现复杂产品零部件关联关系的确定：

面向功能的相关性分析，主要是将实现相同功能的零部件聚合到一个模块中；

面向结构的相关性分析，主要从零部件间的联接及形位关系考虑，将具有紧密联接及形位关系的零部件聚合在一个模块；

面向客户参与度的相关性分析，主要是为满足客户对产品个性化定制的特点，复杂产品的设计过程中，客户通常需要与设计者进行互动沟通，以满足自己的特定需求。根据客户的参与程度将客户参与度较大的部分集中到同一个模块中，进而提高客户的满意度。

对复杂产品零部件进行相关性分析时，需要对指标进行量化处理，特别是对定性指标的定量化处理。由于受决策者专业化水平及经验的影响，定性指标的定量化处理往往存在大量的模糊性与不确定性，为减少模糊不确定性，文章采用梯形直觉模糊数实现定性指标的定量化处理，将诸多模糊性定性指标“很强”、“强”、“中”、“弱”、“很弱”转化为模糊数。将评价语义转化为相应的模糊数并进行定量化处理，不同的评价语义对应的模糊数转化规则如表1所示。

表1 评价语义与模糊集对应关系

基于表1，结合文献[9]，并利用梯形直觉模糊集对结构关系强度定量化处理，定义结构关系评价准则如表2所示。

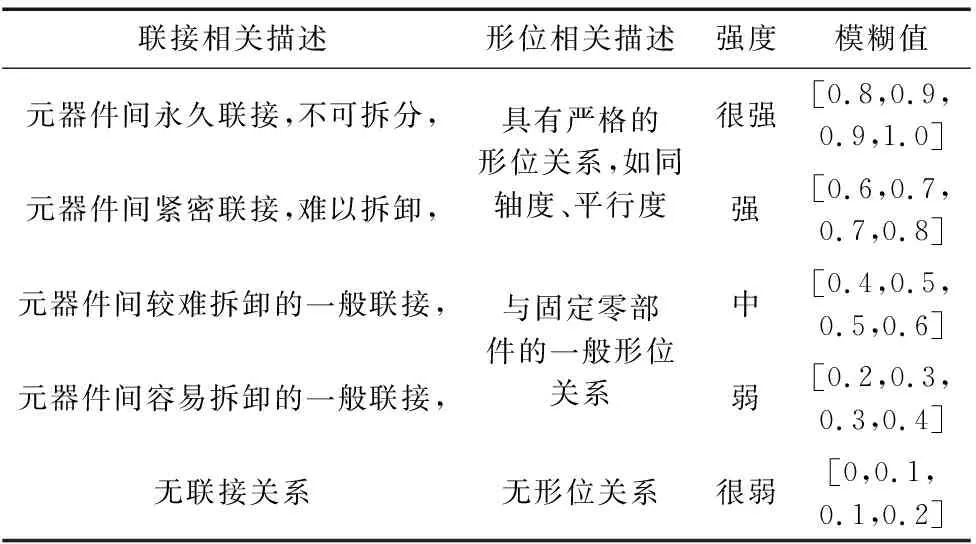
表2 结构相关性评价标准

以各部分之间的结构相关性评价标准为例，进行了简要说明。根据上表，如果零件i与零件j永久联接且具有严格的形位关系，那么就可以定义零件i与零件j之间的结构关系很强，其对应的梯形直觉模糊值为[0.8,0.9,0.9,1.0]。同样，利用梯形直觉模糊集实现功能与客户参与度相关性的定量化处理，定义各自的评价准则。

由专家根据功能与结构评价标准，确立节点之间的关联关系强度，从而得出模块划分的各相关性矩阵。设由评价标准得出的结构相关矩阵为A=(aij)(n×n)，功能相关矩阵为B=(bij)(n×n)，客户参与度相关性矩阵为C=(cij)(n×n)，那么存在产品的综合相关矩阵为:

S=ωaA+ωbB+ωcC

(4)

并且有ωa,ωb,ωc为结构相关性、功能相关性及客户参与度相关性对应的权重，其中:

ωa+ωb+ωc=1

(5)

且ωa,ωb,ωc[0,1]。

文章生成的相关矩阵都用邻接矩阵表示，假设，复杂机械产品由N个零部件组成，并且每个零部件都对应于复杂网络模型中的节点，则有顶点的集合V={v1,v2,…vn}，边的集合E={ei1,ei2,…ein}，边权的集合ω={ωi1,ωi2,…ωin}，ωij表示零件vj与零件vi的具体关系强度大小。对于邻接矩阵有G=(V,E,ω),这里复杂机械产品所对应的网络为加权无向网络，所以相关矩阵都为对称矩阵，且主对角线都为0。

2 复杂网络社团结构算法

本文采用的复杂网络社团结构算法是Fast Unfolding算法，它是由Vincent D.Blondel等[10]于2008年提出，它是一种基于模块度的启发式算法，也是一种层次性贪心算法，该算法的主要目标是为使网络的模块度值不断地增大，将对网络的社区不断地划分。基于Fast Unfolding算法的主要步骤如图1所示。

这里的增益ΔQ主要是划分前后网络模块度的差值，其具体表达式为：

△Q=

(6)

∑in代表社区内部的连线数， ∑tot代表社区节点的度数之和，ki代表与节点i相连接的边的权重之和，m代表社区中边的所有权重。

图1 Fast Unfolding算法流程图

3 应用实例

3.1 案例介绍

以某单位的二级减速器为例，采用本文的方法，求解减速器的模块聚类方案。同时，二级减速器如图2所示。

图2 二级减速器实物图

为了避免零件数量繁多给后期计算带来的难度，由多位经验丰富的设计师及专家讨论，经过对二级减速器的零部件进行预划分。本文采用文献[5]的预划分准则，把二级减速器划分为31个主要部件，对应于二级减速器零部件关联关系的综合矩阵(31×31)。

3.2 模块划分

3.2.1零部件边权赋值

确定零部件综合矩阵之前，首先要确定功能、结构及客户参与度的指标权值。引入改进的模糊层次分析法[11]确定指标权值，改进的模糊层次分析法同时考虑客观数据和决策者的主观经验，克服了层次分析法的缺陷，并且解决了判断矩阵一致性难以满足的问题。最终确定三个指标相关权重见表3(为方便计算，权值取四舍五入)。

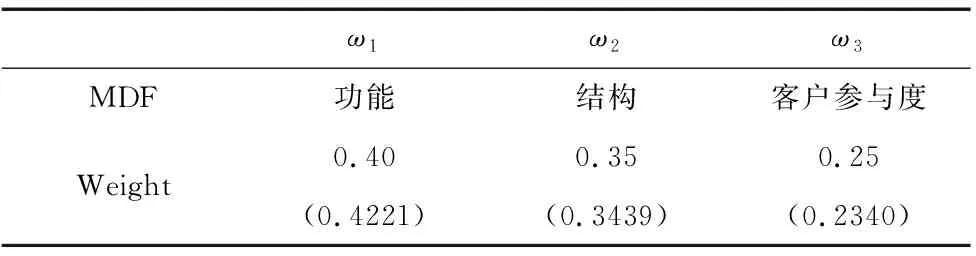
表3 权重分配表

由式(4)得出综合相关性的数据如表4所示,简介表中零部件相关性具体数据由来，如第一行第二列数据，描述的是上箱盖与下箱盖的相关性，上箱盖与下箱盖之间具有较严格的形位关系且联接较为紧密，专家通过表2的结构相关性评价标准，将其相关关系用梯形直觉模糊值表示为[0.6,0.7,0.7,0.8] 上箱盖与下箱盖在功能上共同支撑及固定着轴系零件，将其先关关系用梯形直觉模糊数表示为[0.2,0.3,0.3,0.4]；将客户参与度用梯形直觉模糊数表示为[0,0.1,0.1,0.2]。在标准的梯形直觉模糊数中要求μM=0,ωM=1,且要求决策者对积极情绪或消极情绪不关心，即λ=1/2。然后根据梯形直觉模糊数的打分函数及式(4)得出权值大小0.35×0.781+0.40×0.346+0.25×0.105=0.438(为方便后续计算记为0.44)。

3.2.2 基于Fast Unfolding算法的模块划分

本文选用Gephi 软件来绘制产品的权重复杂网络模型及网络图的模块化分析，建立减速器零部件的权重复杂网络模型。得出二级减速器零部件关系网络模型对应的邻接矩阵(综合相关矩阵)如表4所示；并将减速器零部件的综合相关矩阵导入Gephi软件，通过软件可视化操作生成无向加权网络图，节点布局选择Force Atlas布局，如图3所示。

表4 综合相关矩阵

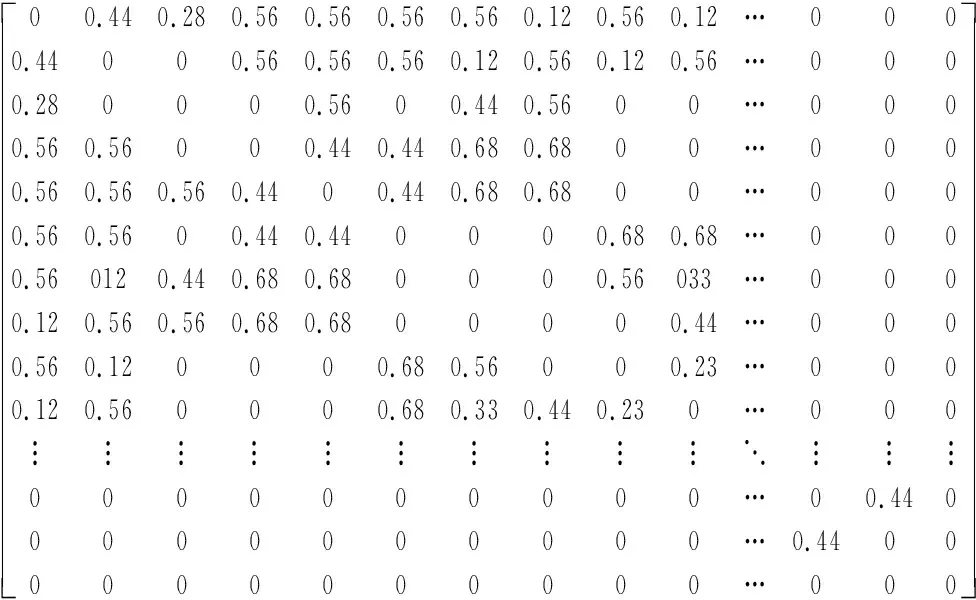
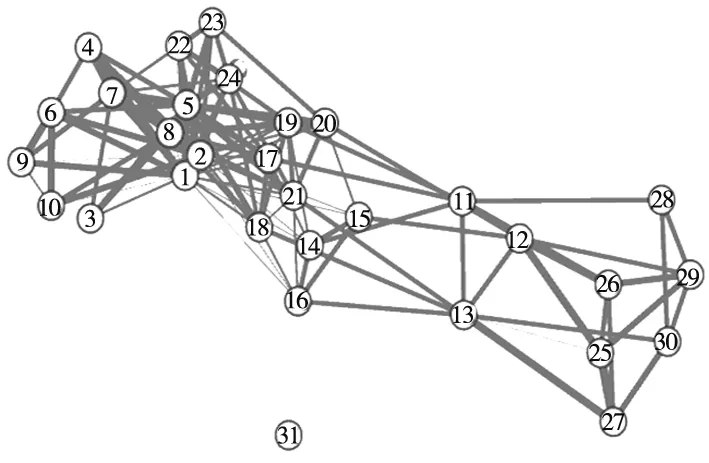
图3 无向加权网络图

运用Gephi软件的Fast Unfolding算法，实现减速器零部件的模块划分。软件读取节点数据与边数据，然后进行模块化操作，通过调整解析度的大小整理模块划分结果如表5所示。

表5 模块划分结果整理

因为Fast Unfolding算法是基于模块度的复杂网络算法，基于模块度的算法，其划分结果存在模块度越大，划分效果越好。根据上表的划分结果，可知当模块度为0.346时，其模块度最大，则认为其对应的划分结果最优。

3.3 划分方案比较

文章采用的是将加权复杂网络应用于产品的模块划分，为证明该方法的有效性，我们对比分析了无权复杂网络形成的划分结果以及聚类划分结果。其中无权复杂网络方法是将减速器零部件间的关联关系用0和1表示，0表示零部件间没有关系，1即表示有关系，将对应的综合矩阵导入Gephi软件，生成的网络图如图4所示。

图4 无向无权网络图

聚类划分结果是使用软件UCINET对减速器零部件进行聚类分析，这里选择的是谱系聚类分析，然后得到聚类分析树状图，如图5所示。

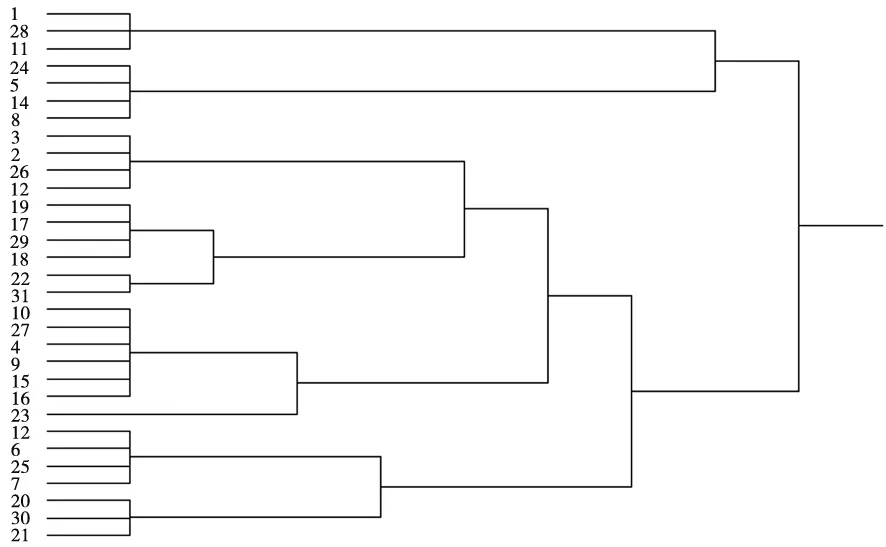
图5 聚类分析结果图

整理三种方法的结果，其中基于Fast Unfolding算法的加权与无权复杂网络生成的模块划分都选择模块度最大的方案，基于谱系的聚类分析选择对应模块数为5的划分方案，统计三种方法具体划分结果如表6所示。

表6 划分方案对比

分别邀请了3位关于减速器设计、制造、装配方面的专家对模块划分方案进行评价，这里采用基于混合模糊集的评价方法实现对以上三个方案的评价，结合文献[12]，分别计算三个方案与其正负理想解的综合相对贴近度，从而获取划分方案的排序，最终获得最优的模块划分方案。具体方案评价结果如表7所示。

表7 相对贴近度

根据相对贴近度的取值进行方案排序，得出备选方案排序结果为，同时获得方案一为最佳方案，即基于Fast Unfolding算法的加权复杂网络得出的模块划分结果更优,进而验证了本文所提方法的有效性。

3.4 划分结果分析

二级减速器主要是在原动机与工作机之间匹配转速及传递转矩，根据方案评价方法并结合减速器零部件的结构特点，对比三种划分方案。方案一将减速器零部件划分为5个基本模块，模块1[1,2,4,6,9,10]主要是箱体模块；模块2[3,5,7,8,17,18,19,20,21,22,23,24]主要是减速器的配件模块，将减速器的端盖、垫片等零部件归于该模块中；模块3[11,12,13,25,26,27,28,29,30]轴系模块，将减速器的轴、轴上的齿轮及键归于该模块内；模块4[14,15,16]，这里将用来支撑与固定轴的轴承单独划分出来；模块5[31]放油螺栓。结合减速器实物图且相比于其他两个方案，发现方案一划分更为合理。综上所述，基于加权复杂网络Fast Unfolding算法的减速器模块划分结果与工程实际更吻合，其划分效果更好。

4 结论

本文主要是研究面向大规模定制的模块划分，考虑模块划分中高耦合、低内聚的原则，文章将复杂网络中的社团结构发现理论应用于复杂产品的模块化分中。基于加权复杂网络理论，构建复杂产品的零部件关系网络模型。为减少模块划分过程中存在的模糊性与不确定性，将模糊集理论引入到模块划分的多属性决策问题中，研究关于产品的结构、功能及客户参与度的关联关系定量化方法，采用基于梯形直觉模糊数计算加权复杂网络的边权；然后，采用Fast Unfolding算法实现复杂机械产品零部件加权复杂网络的模块划分，得到模块划分的最优方案，并通过与无权复杂网络、聚类分析进行对比，验证了该方案的有效性。需要指出的是，关于的产品的模块划分是十分复杂的，尤其是在复杂机械产品中，任何一种划分方法都不能十分精确的实现模块划分，只能是使划分结果不断地实现优化。本文的方法也是如此，所以，此方法的划分结果也只能作为一个参考。分析本文方案一的划分结果，可以发现模块2中螺母及平垫也可以划分到模块1中，对于这种零部件同时属于两个模块的情况，这就涉及到复杂网络中“骑墙节点”的归属问题；所以为提高模块划分方法的准确性，今后需进一步做到：

(1)充分考虑复杂网络的重叠性问题，挖掘重叠社团中的“骑墙节点”，并解决这些骑墙节点的归属问题[13]。

(2)进一步分析Fast Unfolding算法，完善该算法自身的局限性，对其进行改进以实现算法的优化。