一种耦合区间随机混合可靠性分析方法

谢少军 潘柏松 罗路平 项涌涌

浙江工业大学机械工程学院，杭州，310014

0 引言

因试验数据不足，某些不确定性变量采用区间模型描述，如计算误差、试验数据误差、尺寸公差等，这导致可靠性分析既涉及传统的用概率分布函数描述的随机变量，也存在用区间模型描述的区间变量。区间变量在随机-区间混合可靠性分析中导致双层耦合循环，计算效率较低，由此，国内外学者提出了多种高效的随机-区间混合可靠性分析方法。如DU[1]针对随机变量和区间变量的共存情况，利用序列迭代分析方法将耦合的可靠性问题解耦，并基于一次二阶矩法提出一种高效的混合不确定性分析方法(unified uncertainty analysis method based on the first order reliability method，FORM-UUA)；刘帅杰等[2]针对星载可展天线齿轮防卡问题，开展区间与概率变量下的齿轮防卡可靠性的研究；刘海波等[3]提出了一种概率-区间混合不确定性下的串并联系统可靠性分析方法。但多数混合可靠性分析方法均假设区间变量是相互独立的，区间变量可取可行域(由其形状也称为箱形域)内任意值，而在工程实际中某些区间变量的可行域是箱形域的子集，即区间变量是相互耦合的。显然，如果将耦合区间变量简化为独立区间变量，则会增加分析结果的不确定性，产生保守结果。因此，考虑区间变量耦合性，提出耦合区间-随机混合可靠性分析方法具有重要的研究意义。

因区间变量的耦合性，在耦合区间-随机混合可靠性分析中导致关于耦合区间变量优化的区间分析更加复杂，其中，区间分析的计算效率是主要技术难点之一。为提高区间分析的计算效率，LUO等[4]基于单调性假设提出了一种耦合区间变量和随机变量下的高效同步迭代算法，但当极限状态函数关于耦合区间变量非单调时，该迭代算法无法收敛。通过极坐标转换将耦合区间变量转换为独立区间变量，潘柏松等[5]基于投影梯度法提出了一种高效区间分析算法，但该区间分析算法需计算极限状态函数关于区间变量的二阶导数，当耦合区间变量数量较多时，计算效率可能较低，并且极坐标转换较大地增加区间分析优化模型的非线性，可能降低区间分析算法的精度。

为进一步解决混合可靠性分析计算效率低的问题，本文提出了一种高效的耦合区间-随机混合可靠性分析方法。利用序列迭代分析方法，将耦合区间-概率混合可靠性分析的双层耦合优化问题分解为概率分析与区间分析各自依序迭代的两部分，并结合多项式插值法提出了一种适用于极限状态函数关于耦合区间变量单调与非单调两种工况的高效区间分析算法。

1 传统可靠性分析方法

设系统响应G关于随机变量的函数为

G=g(X)

(1)

其中，X表示n维随机变量向量。当G<0时，系统失效，则失效概率Pf可表示为

Pf=Pr{G=g(X)<0}

(2)

其中，函数g(·)称为极限状态函数，Pr{·}表示概率。假设X的联合概率分布函数为fx(X)，通过作失效域Ω={X:g(X)<0}内的积分计算，获得失效概率

(3)

因为失效域的显式表达式往往难以获取，并且上述积分涉及多重积分计算，故失效概率一般很难由式(3)直接求得，通常用近似方法如一次二阶矩法[6-9]进行求解。通过对极限状态函数在标准正态分布空间内的线性近似，一次二阶矩法可高效地求得失效概率的近似值。一次二阶矩法主要包括两个步骤，首先利用以下Rosenblatt转换，将随机变量Xi转换为标准正态分布变量Ui(用大写字母表示不确定性变量，小写字母表示对应的不确定性变量取得某一数值)：

ui=Φ-1[FXi(xi)]

(4)

式中，FXi(·)为Xi的累积分布函数；Φ-1[·]为标准正态分布变量的累积分布函数的逆函数。

在标准正态分布空间内，由以下优化问题求解最大概率点u*：

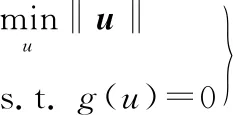
(5)

其中，‖·‖表示向量的模。一旦求得u*，则失效概率

Pf=Pr{G=g(X)<0}≈Φ(-β)

(6)

式中，β=‖u*‖为可靠性指标。

2 混合可靠性分析方法

当随机变量与耦合区间变量共存时，极限状态函数可表示为

G=g(X,Y)

(7)

其中，Y表示由耦合区间变量构成的m维向量，其多椭球模型[10-11]可表示为

(8)

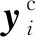
假设耦合区间变量为某一定值，即Y=y，则混合可靠性分析变为传统的可靠性分析问题，其失效概率可表示为

Pf(Y=y)=Pr{G=g(X,y)<0}

(9)

若耦合区间变量在其可行域内变化，则失效概率是关于耦合区间变量的函数。显然，可以从中找到最小和最大失效概率，分别为

Pfmin=Pr{Gmax=g(X,y*)<0}

(10)

Pfmax=Pr{Gmin=g(X,y*)<0}

(11)

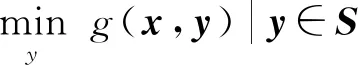
由式(10)与式(11)可见，计算最小与最大失效概率是一个双层耦合循环问题，外层循环是以随机变量为变量的概率分析，用于计算失效概率；内层循环是以耦合区间变量为变量的区间分析，用于求解耦合区间变量优化点。为提高计算效率，采用序列迭代分析方法，将双层耦合循环问题分解为概率分析与区间分析两部分。

在序列迭代分析流程中，概率分析采用前文所述的一次二阶矩法。为降低区间分析的求解难度，首先将耦合区间变量作如下正则化变换：

(12)

其中，i=1,2,…,Ng，vi表示正则耦合区间变量，Qi为正交矩阵，其列向量为Wi的标准特征向量，Λi为对角矩阵，其对角元素为对应的Wi特征值，满足WiQi=QiΛi。将式(12)代入式(8)，可得V的可行域V：

(13)

由此可见，V是量纲一的量，各组耦合区间变量的可行域转换为中心位于坐标原点、半径为1的球模型。

计算最大失效概率的序列迭代分析流程见图1。在第k迭代步时，标准正态分布变量点由最大概率点迭代算法更新，新的正则耦合区间变量由以下优化问题求得：

(14)

图1 序列迭代分析流程图Fig.1 Flowchart of the sequential analysis procedure

为进一步提高效率，在区间分析前，利用式(14)优化问题的Karush-Kuhn-Tucker (KKT)条件，判断初始值是否为优化点，若是则跳过区间分析，并令v(k+1)=v(k)。KKT条件为

(15)

i=1,2,…,Ng

概率分析与区间分析的序列迭代收敛条件为

(16)

其中，ε1、ε2为给定的较小正数。当上述条件满足时，则迭代停止，输出最大概率点u*=u(k+1)，最大失效概率

Pfmax=Φ(-‖u*‖)

(17)

在概率分析中，最大概率点算法采用GONG等[13]提出的迭代计算公式：

u(k+1)=β(k)α(k)

(18)

其中，α(k)表示第k步的单位搜寻方向，即

(19)

搜寻步长

(20)

本文提出了一种高效的区间分析算法，为节省篇幅，仅给出计算最大失效概率的计算公式，计算最小失效概率仅需将式(14)的目标函数g(u(k+1),v)替换为-g(u(k+1),v)。

3 区间分析算法

区间分析算法的任务是高效求解式(14)的优化问题，求得正则耦合区间变量优化点v*。令l表示区间分析算法的迭代步，每次实施区间分析时，迭代步初始化为零，正则耦合区间变量初始点设为v(l=0)=v(k)。

首先，假设优化点位于边界点，则可推导获得以下迭代计算式：

(21)

若满足优化点位于边界点的假设条件，则基于式(21)的迭代式可高效地求得优化点。但若优化点位于可行域内部，则式(21)不能收敛。为此，利用二阶多项式插值法，搜索在连接两个边界点线段内部的优化点。

判断迭代前后极限状态函数响应值是否减小，若g(u(k+1),v(l+1))>g(u(k+1),v(l))，则表明新的迭代点没有降低目标函数响应值，反而比旧的迭代点效果更差，则舍弃新点，而通过沿旧点的梯度反方向搜索新的边界点：

(22)

Gvi=gvi(u(k+1),v(l))i=1,2,…,Ng

其中，系数ai为非负数，表示为

(23)

(24)

图2 迭代点相互重合示意图Fig.2 Two sequentially iterative points coincide

基于式(22)或式(24)获得新迭代点后，比较目标函数响应值。若g(u(k+1),v(l+1))≤g(u(k+1),v(l))，则判断是否满足KKT条件，若满足，则区间分析迭代停止，输出v(k+1)=v(l+1)；否则，令l←l+1，并基于式(22)或式(24)继续迭代计算。

若g(u(k+1),v(l+1))>g(u(k+1),v(l))，则建立二阶多项式插值函数，搜索连接v(l+1)与v(l)线段内部的极小值。基于线段端点处信息，建立以下二阶多项式插值函数：

gq(t)=a+bt+ct2

(25)

其中，t表示线段内的位置参数，满足0≤t≤1。令t*为线段内局部优化点，则满足

(26)

gq(0)=g(u(k+1),v(l))

g′q(0)=(v(l+1)-v(l))Tgv(u(k+1),v(l))

gq(1)=g(u(k+1),v(l+1))

则对应t*的迭代点为

v(l+1)=(v(l+1)-v(l))t*+v(l)

(27)

检查v(l+1)是否满足KKT条件，若满足则迭代停止，输出v(k+1)=v(l+1)；否则，令l←l+1，并基于式(22)或式(24)继续迭代。区间分析算法的流程图见图3。

图3 区间分析算法流程图Fig.3 Flowchart of the proposed interval analysis algorithm

4 算例

本文采用两个算例来验证提出的混合可靠性分析方法的精度与计算效率。分析方法中，采用有限差分法计算极限状态函数的梯度，并采用调用极限状态函数的次数来评定分析方法的计算效率。

为验证提出的区间分析算法的计算效率，在算例中对本文方法与FORM-UUA方法进行比较分析。虽然FORM-UUA方法被提出时用于处理独立区间变量，但该方法在区间分析中采用了常规非线性优化算法序列二次规划法，用于求解关于区间变量的极值优化问题，故该方法同样适用于耦合区间变量。

4.1 连杆滑块机构

对文献[1]中的连杆滑块机构算例作适当修改，用于验证本文方法的计算精度与效率。如图4所示，滑块受到水平力p作用，当连杆最大应力超出材料许用应力S时，连杆滑块机构失效，则极限状态函数可表示为

其中，l1为曲柄长度；l2为连杆长度；d1、d2分别为圆筒连杆的内外径；S、p、l1、l2为随机变量，其分布参数见表1。

表1 随机变量分布参数

图4 连杆滑块机构Fig.4 A crank-slider mechanism

因机构安装地点不定，偏移量、滑块与地面的摩擦因数被设为区间变量，而圆筒连杆的内外径设为耦合区间变量，则多椭球模型为

Y=[Y1Y2Y3Y4]T=[eμd1d2]T

Y3=[Y3Y4]T

由蒙特卡洛法、FOMR-UUA方法与本文方法计算得到的最大失效概率见表2。使用蒙特卡洛法时，将耦合区间变量的区间划分为50等份，在每种满足可行域的耦合区间变量组合下，对随机变量作106次抽样，计算失效概率，挑选出最大值为最大失效概率。以蒙特卡洛法的计算结果为参照，FORM-UUA方法与本文方法在相同的迭代步下均得到了较准确的结果。然而，由调用极限状态函数的次数Nc可见，本文方法比FORM-UUA方法效率高。

表2 最大失效概率

为进一步分析提出的区间分析算法的有效性，在迭代步k=0时，区间分析算法的历史迭代记录见表3，表3中最后一列表示迭代点是否满足KKT条件，数值为0则表示不满足，为1则表示满足。可见，正则耦合区间变量优化点位于可行域边界，满足优化点位于边界点的假设，因此，本文区间分析算法仅需较少的迭代就可快速求得优化点，计算效率较高。

表3 区间分析算法历史迭代记录

4.2 悬臂圆筒

通过修改文献[1]中的悬臂圆筒算例，验证本文可靠性分析方法。如图5所示，悬臂圆筒受到外部力F1、F2、p与扭矩T。当圆筒最大von-Mises应力σmax超出材料屈服强度Sy时悬臂圆筒失效，则极限状态函数为

G=g(X,Y)=Sy-σmax

图5 悬臂圆筒Fig.5 A cantilever tube

最大von-Mises应力σmax位于悬臂圆筒支撑附近，计算公式为

M=F1L1cosθ1+F2L2cosθ2

τzx=Td/(2J)J=2I

式中，L1为圆筒长度；L2为外力F2作用点距悬臂圆筒根部的距离。

随机变量的分布函数参数见表4。因信息量不足，力的角度θ1与θ2(单位为度)设为耦合区间变量，其多椭球模型为

Y=[Y1Y2]T=[θ1θ2]T

由蒙特卡洛法、FORM-UUA与本文方法计算得到的结果见表5。由表5可见，FORM-UUA方法与本文方法的精度均较高，但本文方法比FORM-UUA方法的效率有较大幅度的提高。

表4 随机变量分布参数

表5 最大失效概率

同理，在迭代步k=0时，区间分析算法的历史迭代记录见表6。由表6可见，正则耦合区间变量优化点位于可行域内部，未满足优化点位于边界点的假设，因此，区间分析算法在迭代步l为3、5时调用了二阶多项式插值法，用于搜索位于可行域内部的优化点，并在l=5时求得优化点。

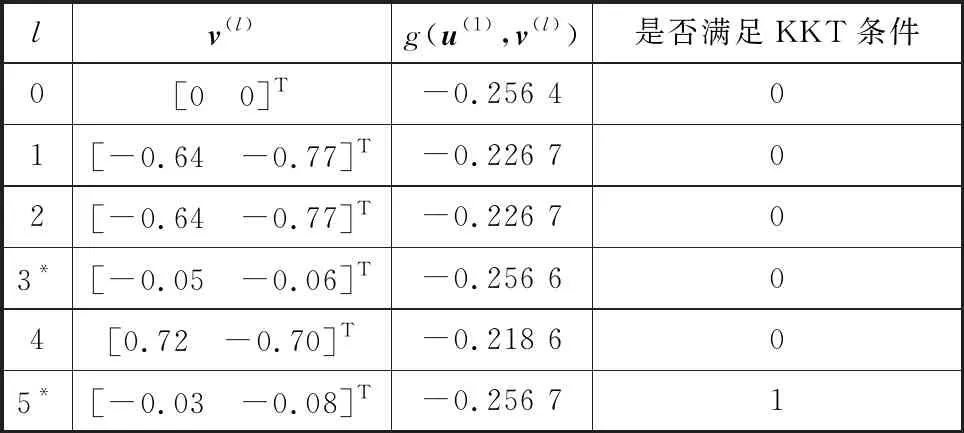
表6 区间分析算法历史迭代记录

注：*表示由二阶多项式插值函数获得。

5 结论

算例结果表明，相比已有算法，本文耦合区间-随机混合可靠性分析方法具有更高的计算效率，提出的区间分析算法可明显提高混合可靠性分析的整体计算效率，并且该方法可适应于耦合区间变量与独立区间变量，应用范围较广。