点接触弹流润滑条件下表面弹性变形研究

沈锦龙 薛正堂 衡传富 刘小君

1.合肥工业大学摩擦学研究所，合肥，230009 2.阜阳轴承有限公司，阜阳，236000

0 引言

点接触摩擦副广泛应用于机械设备传动机构中，其主要润滑形式为弹流润滑。提高润滑油膜厚度是点接触摩擦副性能优化、寿命延长的关键。弹流润滑状态下的油膜厚度和压力分布与表面形貌紧密相关[1-2],即使是尺度很小的表面粗糙度(小于润滑油膜厚度)也会使压力和膜厚产生较大的波动[3]。点接触区域小、压力大，两接触界面必然会发生不可忽视的弹性变形[4-5],对接触区弹性变形特征进行研究有助于弹流润滑性能的分析和改善。

国内外学者针对表面形貌影响弹流润滑性能这一命题已进行了大量理论与实验研究。早期研究中用均方根粗糙度Rq定量表征表面形貌，用参数Λ和κ描述表面粗糙度与润滑油膜厚度之间的关系，预测效果较为粗略[6-7]。随着计算机技术的发展，粗糙表面弹流润滑问题的数值求解变得更为精细[8]，但由于计算效率低下(一个真实粗糙表面的计算时长可达数天[9])，不适合在工程实践中直接采用。为此，部分研究者致力于发展弹流润滑问题的快速算法。VENNER等[10]将傅里叶分解的思想引入表面形貌分析，提出了一种名为幅值缩减(amplitude reduction，AR)的方法，将复杂的真实粗糙表面分解为一组波长、幅值各异的正弦表面，借助曲线拟合实现了表面弹性变形、膜厚和压力分布的快速预测，例如，对某一512×512点数的表面仅需数秒的计算时间。

在得到表面形貌与弹流润滑性能之间的关系后，可以进行微织构的主动设计，通过微织构改善表面性能，满足特定的应用需求[11-12]。微织构在面接触摩擦副中的应用研究较为充分，而对于点、线接触，微织构的作用机理仍然不甚明朗。某些情况下，在高副中引入微织构能有效地减小摩擦、磨损，而在另一些例子中则呈现出完全相反的效果[13]。因此，这一命题还需要进一步深入研究。对于弹流润滑，尤其是有表面微织构的弹流润滑研究，对表面形貌的变形缺少定量描述，很难深入分析形貌变形特征及其对润滑性能的影响，不利于揭示点接触状态下表面织构的作用机理[14]。

本文以6010深沟球轴承为对象，采用激光微织构法制备了一组形貌各异的滚道表面试件，通过光学显微镜获取表面原始三维轮廓数据，结合AR算法与快速傅里叶变换，计算出不同工况下的变形后表面，并基于ISO 25178[15]三维形貌参数体系对变形前后表面进行表征，研究工况变化对弹流接触弹性变形的影响，以及由弹性变形引发的表面性能变化。

1 理论基础

点接触运动形式的机械零件如滚动轴承，在一定运转条件下可实现弹流润滑状态。这类零件的表面损伤与润滑状态紧密相关。油膜的形状、油膜厚度、油膜压力分布、温度场及摩擦力等直接影响表面是否出现胶合、擦伤和接触疲劳失效等形式的损伤。因此，弹流润滑状态对改善点接触摩擦副的工作性能并延长服役寿命有重要影响。弹流润滑的理论基础是Reynolds润滑理论和Hertz弹性接触理论。

等温条件下点接触稳态弹流润滑的Reynolds方程简化形式为

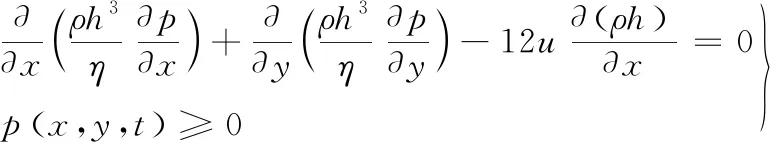
(1)

其中，ρ为润滑油的密度，kg/m3;η为润滑油的动力黏度，Pa·s;u为两表面切向速度的平均值，m/s;h为考虑了表面弹性变形的膜厚。对于弹性点接触问题，膜厚计算公式为

(2)

其中，Rx、Ry分别为接触界面在x和y方向上的当量曲率半径，E′为当量弹性模量，Pa。R(x,y,t)为表面未发生弹性变形时的真实形貌，其形貌高度幅值用Ai表示。δ(t)为在油膜压力p作用下表面发生的弹性变形。当载荷恒定且忽略惯性效应时可以得到总载荷w2：

(3)

VENNER等[10]经过理论研究，采用曲线拟合法获得了弹性变形后表面形貌幅值Ad与变形前幅值Ai之间的关系，即Amplitude Reduction(AR)公式。幅值比的具体形式为

(4)

上式中的关键变量计算公式为

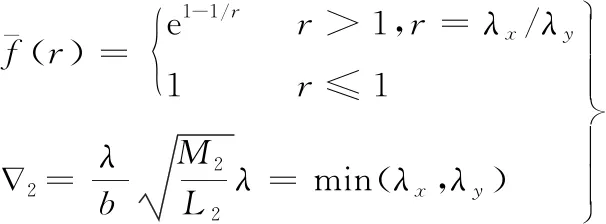
(5)

其中，λx、λy分别为正弦波在x和y坐标上的分量。从式(5)中可看出，2的值与表面谐波波长λ、Hertz接触半宽b和量纲一Moses参数M2、L2有关。载荷参数M2和润滑参数L2可以代表工况条件的影响，其表达式分别为

(6)

式中，α为黏压系数，m2/N；η0为大气压下的润滑油黏度。

2 表面形貌的重构过程

结合AR公式和下述表面形貌重构方法，可复现点接触条件下表面形貌在润滑接触过程中的弹性变形情况。

设三维粗糙表面的表达式为z(x,y)，z表示表面高度值，x和y分别为接触区沿相对运动方向和垂直运动方向的坐标值。从信号处理角度来看，z(x,y)是一个由独立变量x和y决定的随机信号。由于是点接触界面，对其进行二维傅里叶变换可得到一系列二维正弦波形，这意味着表面粗糙度可以分解为一系列正弦波的叠加，即

Z(ω)=A(ωxx-ωyy)=

Aicos(ω(xcosθ-ysinθ))

(7)

Z(ω)可看作三维粗糙表面z(x,y)的一个频率分量，它在x和y坐标方向分量的频率分别为ωx和ωy，它的几何特征由高度幅值Ai、频率ω和相位角θ所决定。结合AR公式，可以得到接触过程中的粗糙表面弹性变形情况，具体步骤如下。

对粗糙表面测量数据进行快速傅里叶变换(fast Fourier transform,FFT)，得到弹性变形前形貌的频率分量：

Z(ω)=FFT(z(x,y))

(8)

利用AR公式计算得到特定工况下各谐波频率对应的降幅幅度θ，对频率分量进行降幅，得到发生弹性变形后的表面粗糙度频率分量：

Z′(ω)=Z(ω)θ(ω)

(9)

对变形表面频率分量进行快速傅里叶逆变换(inverse fast Fourier transform,IFFT)，获得该工况条件下的弹性变形粗糙表面数据Z′(x,y)：

Z′(x,y)=IFFT(Z′(ω))

(10)

利用MATLAB编写程序得到弹性变形后的表面，重构流程图如图1所示。

图1 表面重构流程Fig.1 Flow chart of surface reconstruction

3 结果与讨论

3.1 表面形貌弹性变形分析

本文研究的接触界面为6010深沟球轴承的钢球与内滚道界面。利用YLP-F10光纤激光打标机和标准旋转工作台对轴承内滚道表面进行微凹坑加工，制造一组形貌、参数各异的表面试件。各试件凹坑的面积占有率均为20%，凹坑直径和深度参数见表1。表面试件加工完成后需去毛刺并用超声清洗微凹坑内的残渣。使用Talysurf CCI Lite非接触式三维光学轮廓仪对织构表面进行测量，获得原始表面形貌。参考6010深沟球轴承的额定动载荷和额定转速，确定计算使用的工况参数。载荷值范围为1～13 kN，转速范围为1 000～9 000 r/min。根据轴承几何参数和各钢球承担的载荷比例[16]，计算出承载比例最高的钢球与滚道间的相对运动速度和正压力，用于后续计算。现以试件1为对象，分析点接触全膜润滑条件下表面形貌的弹性变形。

图2a所示为试件1的原始形貌，图2b所示为载荷10 kN、转速5 000 r/min下产生弹性变形后的表面形貌。图2c所示为变形前后微凹坑深度变化，变形后的凹坑深度值降低、表面形貌呈平坦化趋势，且这种平坦化趋势随着转速的减小和载荷的增大而愈加明显。

表1 激光微织构参数

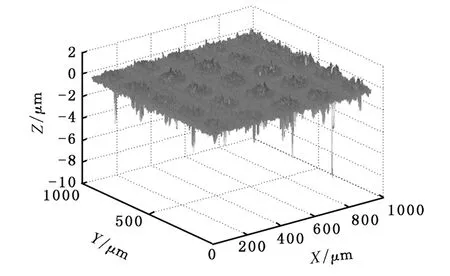
(a)变形前表面

(b)变形后表面

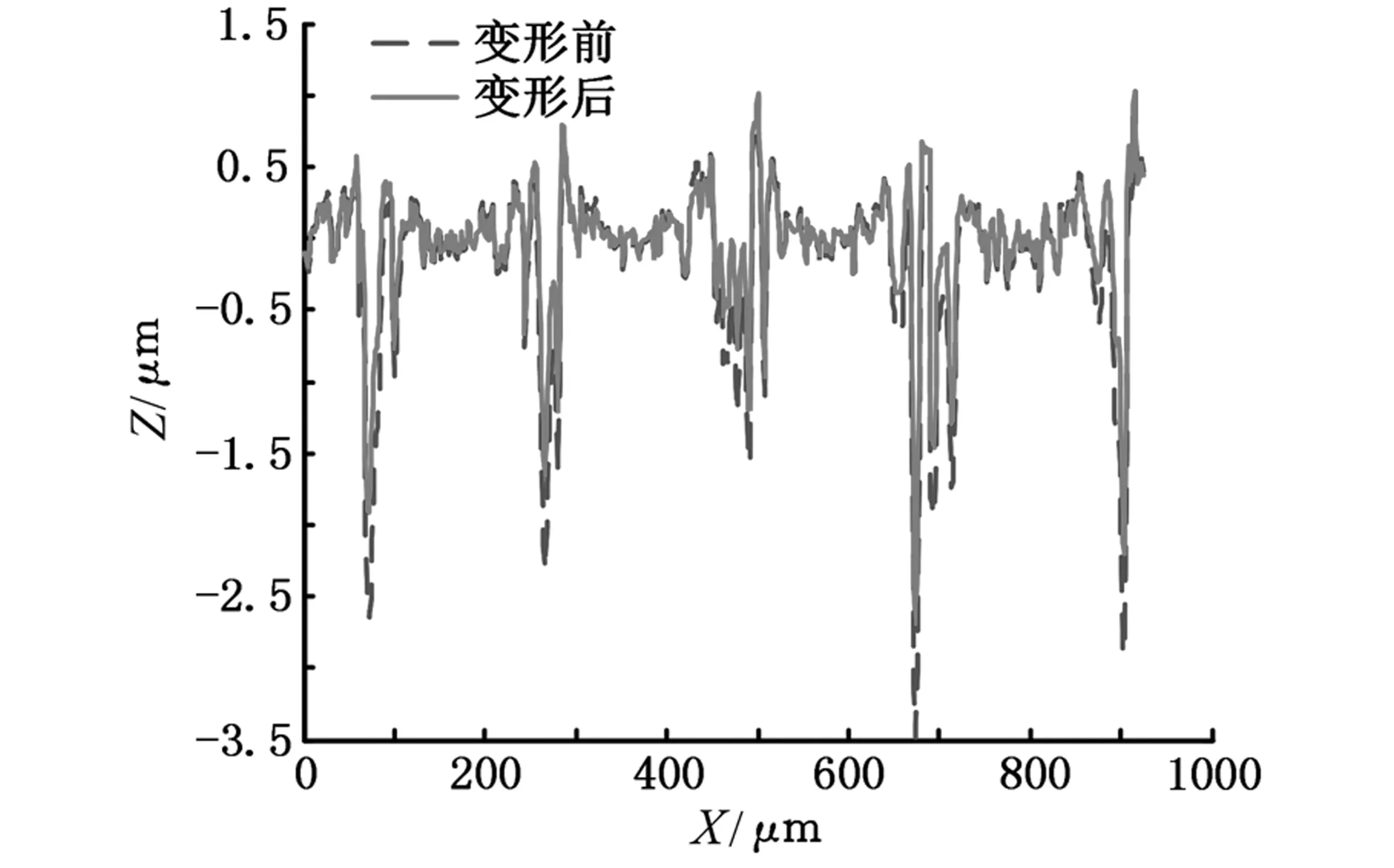
(c)变形前后表面二维对比图2 滚道表面变形前后轮廓的3-D和2-D表面形貌对比Fig.2 3-D and 2-D view of comparison between original surface and deformed surface under EHL pure rolling condition

对原始形貌和变形后形貌进行二维傅里叶变换，结果如图3所示。各频率分量的幅值在变形后有所减小，其中位于中心的低频分量缩减最为显著，高频分量几乎不变，这也符合AR理论中频率越低、降幅越大的预测。分析式(4)和式(5)，降幅比与表面波长λ成负相关关系，即降幅比与表面频率成正相关关系。频率越低的分量，降幅比越小，表面变形量越大，对应图3a、图3b的中心区域，可以看到明显的塌陷；相反，频率越高的分量，表面变形小，对应图中边缘区域，表面幅值几乎没有减小。

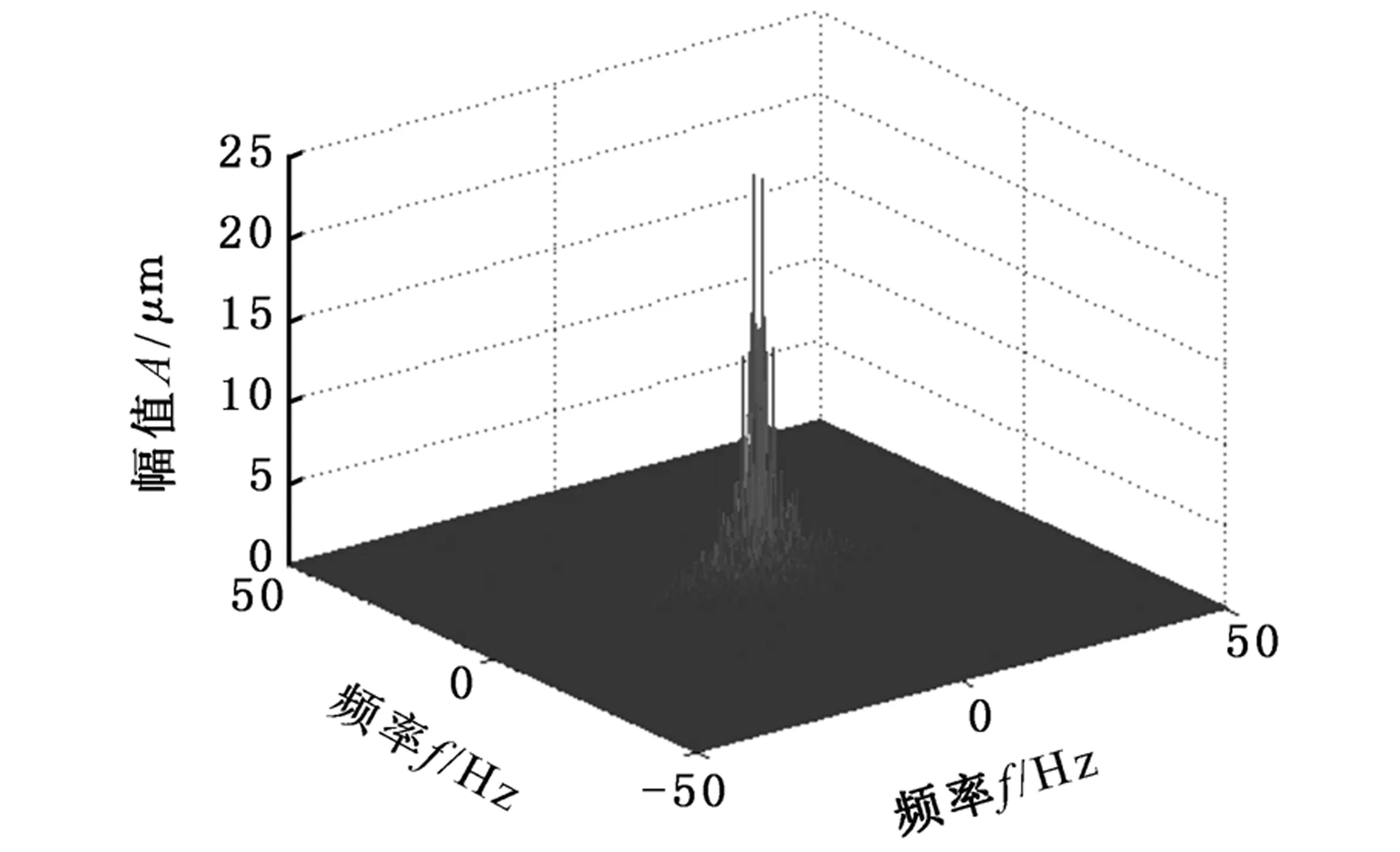
(a)变形前表面频域图

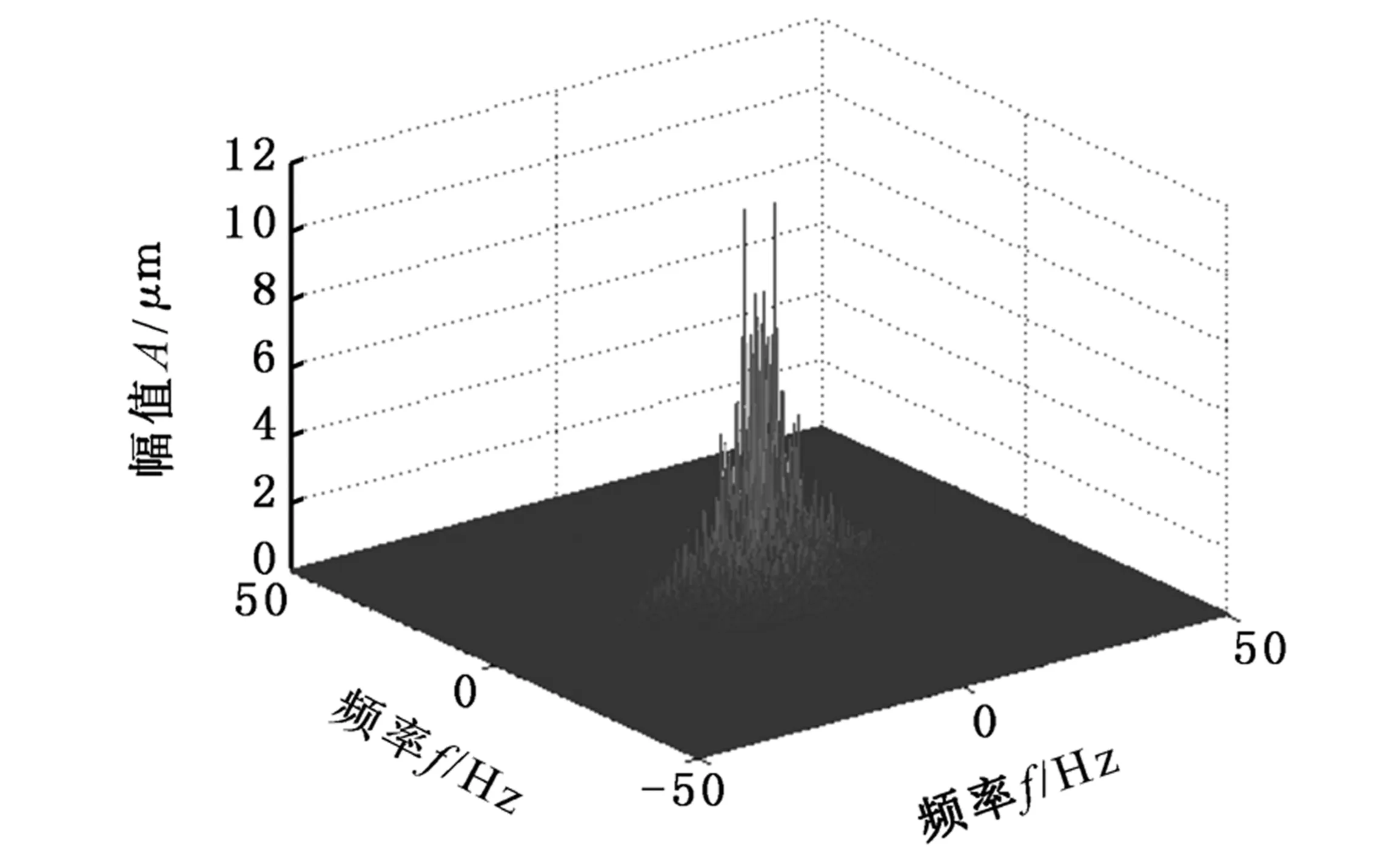
(b)变形后表面频域图图3 滚动表面变形前后轮廓的频域对比Fig.3 Comparison of origin and deformed surface in frequency domain

3.2 表面形貌的表征与变形规律

为了更加准确地分析表面形貌弹性变形特征，本文选取ISO 25178产品几何技术规范中的若干三维形貌参数对变形前后的表面形貌进行定量表征。在高度参数中选取表面高度算术平均偏差Sa、表面高度分布的偏态Ssk和表面高度分布峰态Sku。在空间参数中选取最快衰减自相关率Sal和表面纹理纵横比Str。在功能参数中选取核心区材料体积Vmc和核心区空体体积Vvc。根据6010深沟球轴承的额定动载荷和额定转速，分析了6 000 r/min转速时各形貌参数随载荷的变化规律，以及7 kN载荷时各形貌参数随转速的变化规律。

不同转速和载荷下，变形前后表面Sa的变化情况如图4所示。Sa是由工程中最常用的二维粗糙度参数Ra推广而来的，是表面粗糙程度的总体度量。可以发现，弹流润滑条件下的表面Sa均小于原始形貌的表面Sa，这符合表面平坦化的变形规律。随着载荷的增大，表面Sa值逐渐减小(图4b)，根据弹流润滑及赫兹接触理论，正压力的增大必然导致接触压力的增大(图4a)，从而使得表面弹性变形随之增大、表面形貌平坦化加剧，导致表面高度算数平均偏差Sa逐渐减小。随着转速的增大，表面Sa值逐渐增大。原因可能是：相对运动速度对接触区压力分布产生了影响，随着速度的增大，压力分布沿相对运动方向不断延伸,由于总载荷不变、故受力面积增大，平均压力随之减小，表面轮廓由受压平坦化状态逐渐恢复，从而形成了Sa与速度的正相关关系。

(a)转速对Sa的影响

(b)载荷对Sa的影响图4 转速和载荷对Sa的影响Fig.4 Effect of rotating speed and load on Sa

空间参数Sal和Str随载荷、转速的变化特征如图5所示，这两个参数的变化体现了表面纹理在波长和方向性方面的变化特点。Sal主要由表面的空间频率(波长)成分决定，Sal值较小说明表面由高频(短波长)成分占主导；反之，则表面由低

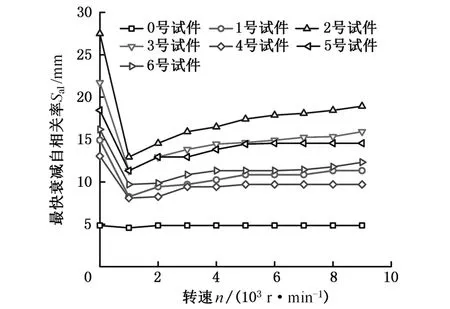
(a)转速对Sal的影响

(b)载荷对Sal的影响

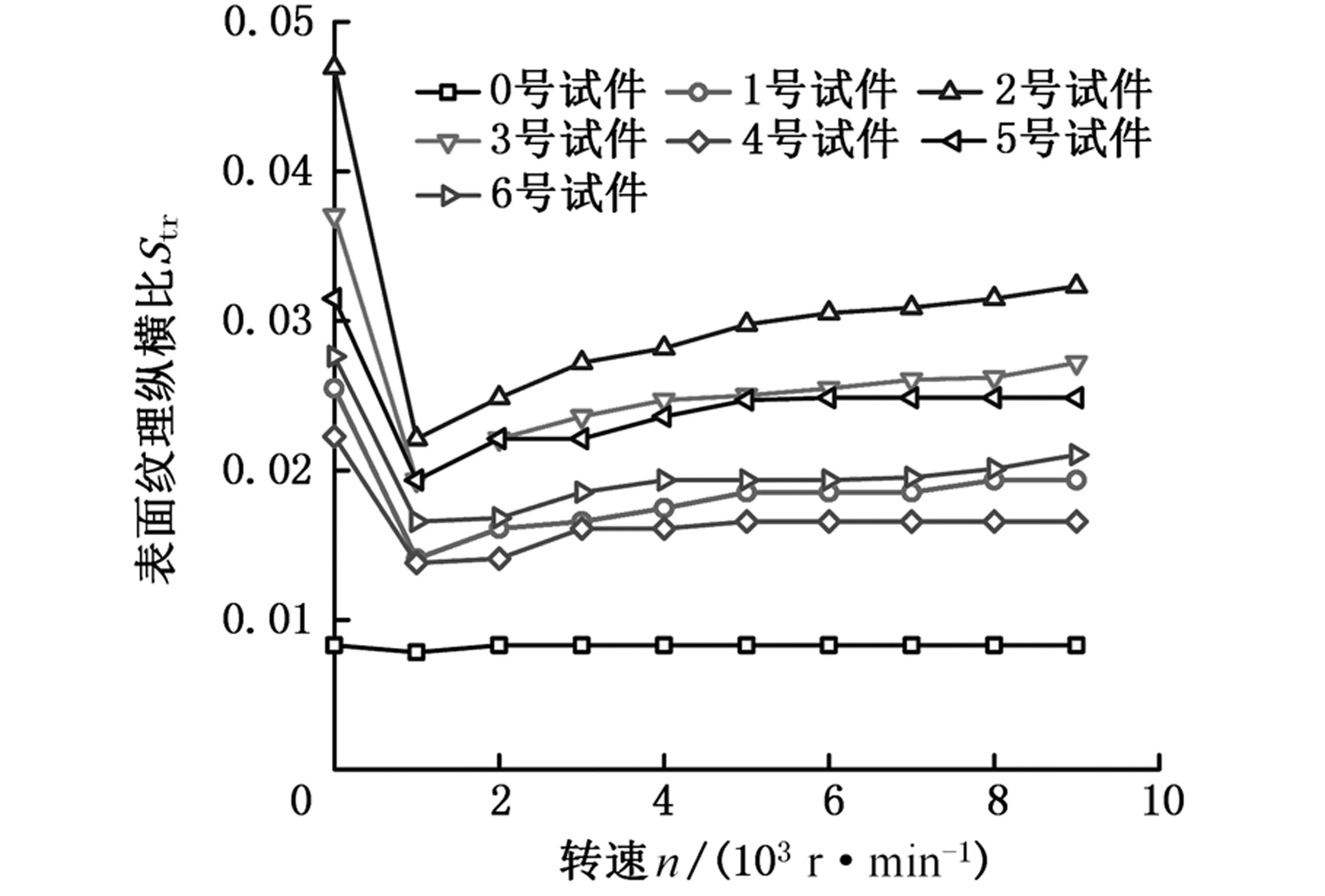
(c)转速对Str的影响

(d)载荷对Str的影响图5 转速和载荷对Sal和Str的影响Fig.5 Effect of rotating speed and load on Sal and Str

频(短波长)成分占主导。Str用来辨识表面在各方向上是否具有相同的纹理，一般认为Str>0.5的表面为各向同性表面，Str<0.3的表面为各向异性表面。图5a、图5b中，Sal初始值相差很大的表面在弹性变形后Sal值相对集中，不论表面初始形貌如何，在弹流润滑状态下都会变为低频成分占主导。AR理论中各频率成分的降幅比与频率直接相关，频率越低，降幅越显著，即使原始表面低频成分占主导，幅值的显著下降也会使低频成分对表面的贡献度降低，转为高频成分占主导。图5c、图5d中的表面纹理纵横比Str表现出了与Sal类似的变化规律。与静态的赫兹接触模型不同，弹流润滑的两表面存在相对运动。无论是压力分布还是弹性变形，都会沿速度方向按一定规律分布，各表面在弹流接触下各向异性都变得更加显著。总体来看，弹流润滑引起的接触变形，使空间参数Sal和Str产生了趋同变化。

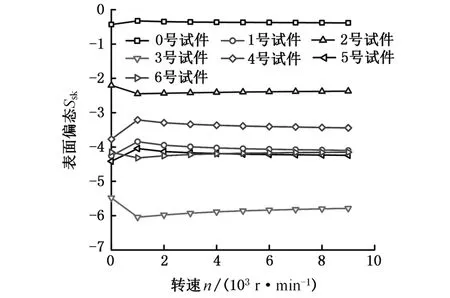
不同转速和载荷下，变形前后表面Ssk和Sku的变化情况如图6所示。Ssk用于检验表面关于基准面的对称性，Sku则用来指示表面是否存在高峰或低谷。如图6a、图6b所示，不论原始表面还是织构表面，偏态Ssk都没有因为弹性变形产生较大的变化，且随工况参数的变化也很小，没有出现负偏态到正偏态的转化，因此，弹性变形对表面偏态的影响很小，可以忽略不计。相反，弹性变形对Sku的影响要大得多，如图6c、图6d所示。织构表面和原始表面呈现出相反的规律，进入弹流接触区后，原始表面的Sku值虽然变化不大，但总体上比不受载时略有减小。相反，织构表面的Sku值则增大了，且总体上原始Sku值越大的表面，变化也越剧烈。Sku值增大说明表面存在更多的尖峰的和深谷，因而与对磨表面产生实体接触的风险也上升了。

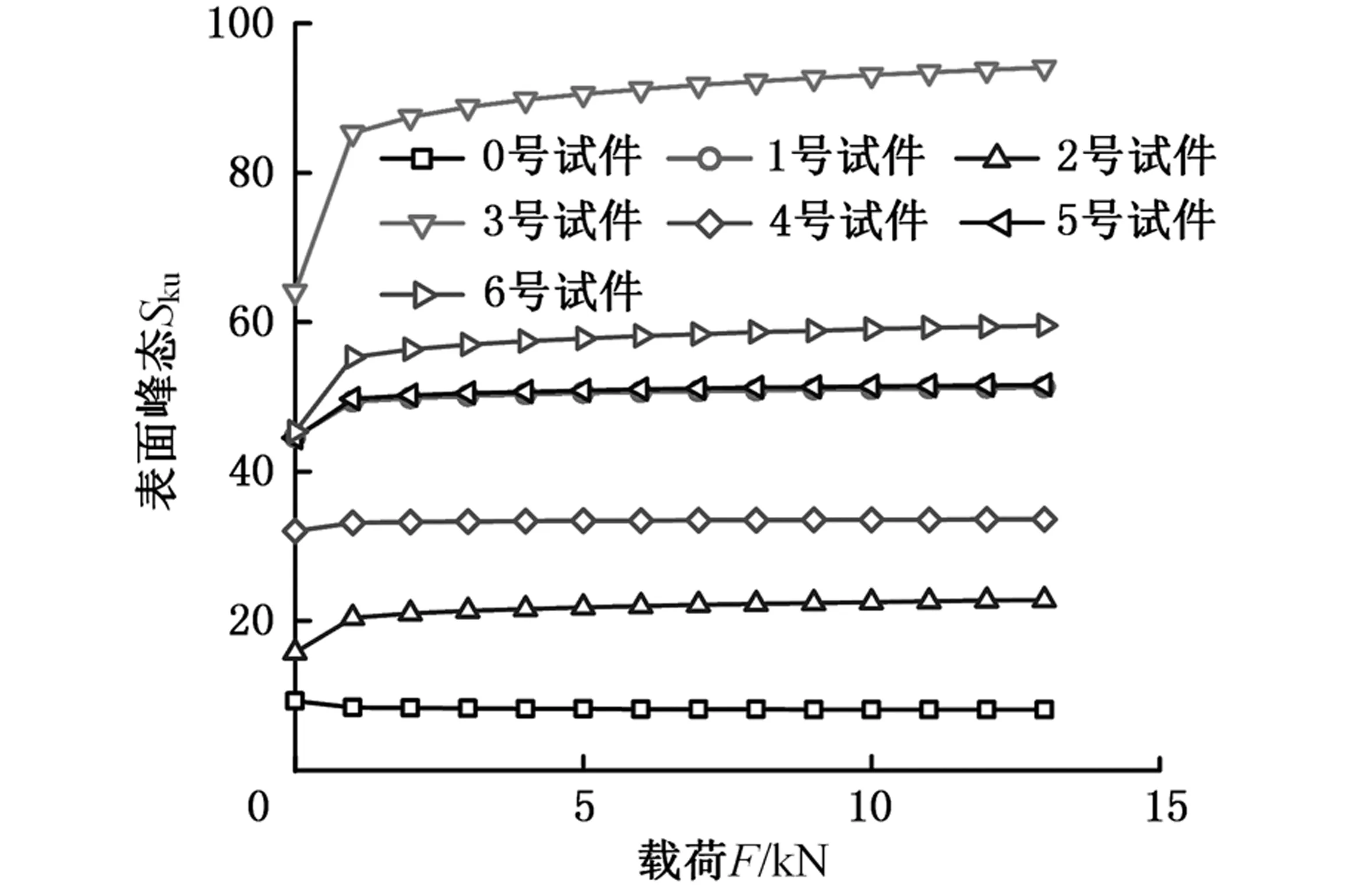
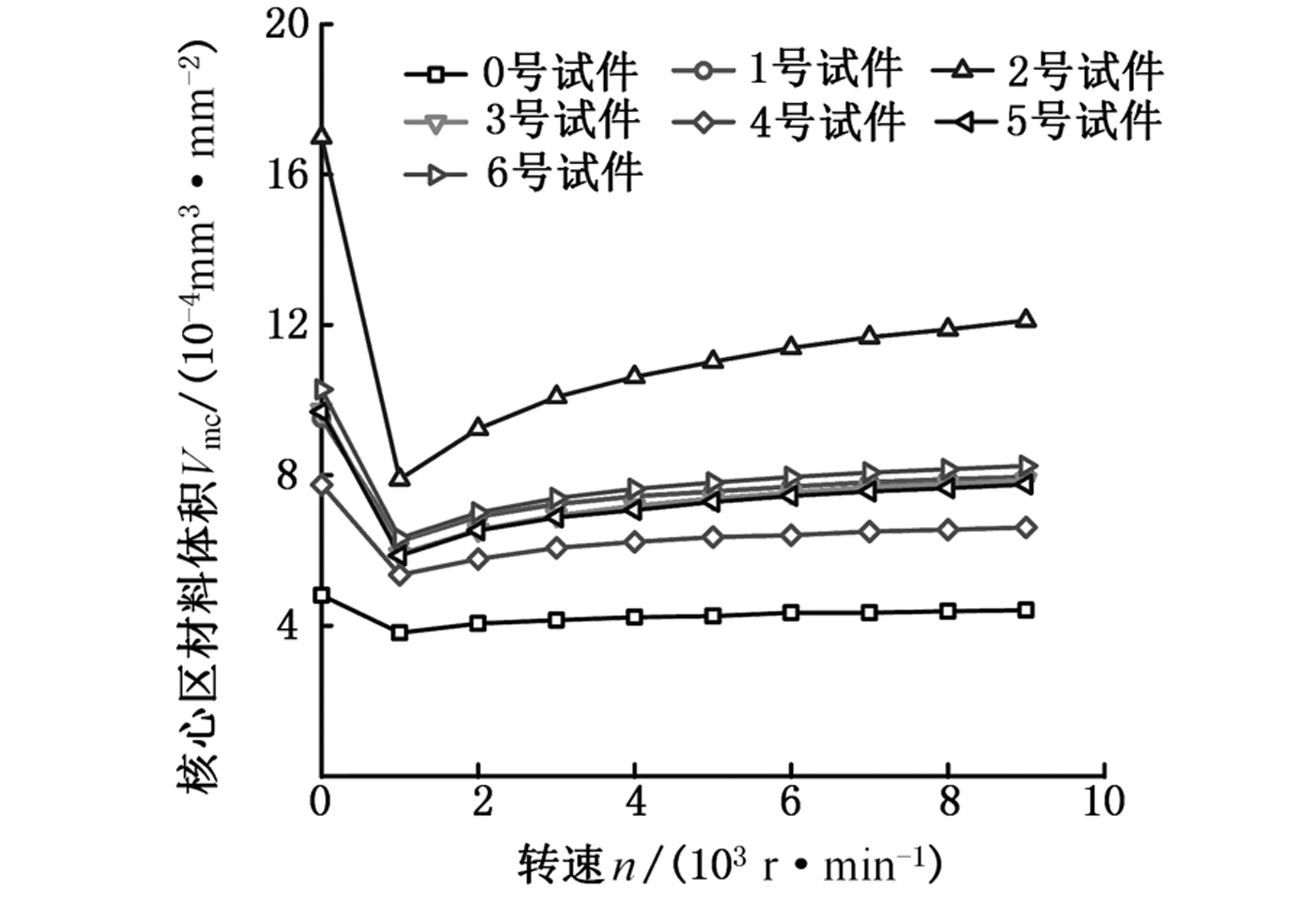
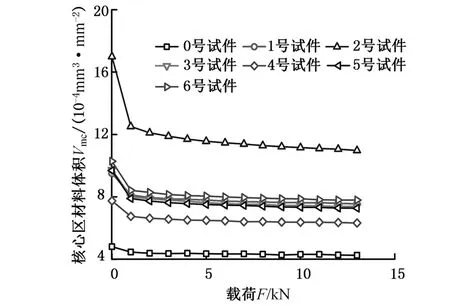
功能参数Vmc和Vvc随载荷、转速的变化情况如图7所示，这两个参数与支承率曲线相关，分别表示支承率在10%～80%之间的材料和空体平均体积，一般情况下，两者之和是一个定值，即支承率10%和80%之间的高度值。在弹流接触状态下，Vmc和Vvc两个参数较变形前都有所减小，说明支承率10%～80%之间的高度值减小，支承率曲线发生了改变。一般认为，相同承载下，Vmc越大，表明表面的耐磨性能越好；Vvc越大，表明表面的储油能力越强、润滑效果越好。弹流接触产生的变形对表面的耐磨性能和润滑特性均有所削弱，且Vvc相比Vmc下降更显著，即空体和实体体积都减小的情况下，实体体积占比升高，变形对表面储油性能的影响更大。在富油润滑状态下，摩擦副表面被一层润滑油覆盖，表面的微凹坑内也被润滑油充满，进入弹流接触区后，表面的核心区空体体积突然减小，储油能力下降，必然导致凹坑内部分润滑油被挤出，使局部油膜压力、油膜厚度均增大。

(a)转速对Ssk的影响

(b)载荷对Ssk的影响

(c)转速对Sku的影响

(d)载荷对Sku的影响图6 转速和载荷对Ssk和Sku的影响Fig.6 Effect of rotating speed and load on Ssk and Sku

(a)转速对Vmc的影响

(b)载荷对Vmc的影响

(d)载荷对Vvc的影响图7 转速和载荷对Vmc和Vvc的影响Fig.7 Effect of rotating speed and load on Vmc and Vvc

4 结论

(1)弹流接触产生的弹性变形使接触表面平坦化，且平坦化趋势随着载荷增大和转速减小愈加剧烈。对于转速较低或载荷较大工况下的滚动轴承织构设计，应考虑弹性变形带来的形貌变化。

(2)弹性变形使表面的频率成分发生变化，趋向于高频成分占主导，且表面的各向异性更加显著。在形貌设计中短波长成分能更有效地改善滚动轴承的摩擦学性能。

(3)表面偏态在变形后几乎没有变化，织构表面峰态呈现出原始值越大，进入接触区后上升越显著的变化特征。在轴承表面处理中应当严格控制峰态值，避免接触变形导致峰态增大，进而导致润滑失效的风险。

(4)弹性变形改变了表面的支承率曲线，核心区(支承率10%～80%)的高度值减小，其中空体体积减小更加显著，即表面的储油性能受到更大的削弱。在进行以提高润滑效果为目的的织构设计时，应考虑核心区空体体积减小引起的储油能力下降问题。