新型RR-RURU踝关节康复机器人机构的设计与分析

张彦斌 荆献领 韩建海,2 陈子豪

1.河南科技大学机电工程学院，洛阳，471003 2.河南省机器人与智能系统重点实验室，洛阳，471023 3.机械装备先进制造河南省协同创新中心，洛阳，471003

0 引言

并联机构是近年来国内外机构学和机器人领域研究的热点之一[1-3]，纯转动并联机构是其中一种特殊类型，其动平台仅有两个或三个转动自由度，可对机械或机器末端操作手的姿态进行调整，已广泛应用于医疗器械[4]、卫星天线随动装置[5]、并联式球面仿生踝关节[6]等需要空间姿态调整的场合。

无耦合并联机构是指机构速度雅可比矩阵为对角阵的一类可约并联机构[7]，因其在运动和力传递方面所表现出的优越性，吸引了越来越多学者的关注。范彩霞等[8]设计了一种无耦合2R并联机构，并利用正逆雅可比矩阵对其奇异性进行分析。JIN等[9]对一类2T2R和3T2R并联机构进行研究，并对其运动学和工作空间展开分析。ZHANG等[10]提出了一种2T1R并联机构，利用灵巧性图谱对机构进行了各向同性设计。

踝关节康复机器人执行机构的主要形式有两种，即基于并联机构式和基于外骨骼式[11]。前者主要用于扭伤脚踝的康复，其典型特征是将患者的脚固定在并联机构的动平台上；后者通常用于步态恢复[12-13]，允许患者穿上机器人，其底基和末端执行器被连接到横跨脚踝的不同肢体上，然而这种结构形式增加了控制设计的难度。目前，国内外学者已基于并联机构设计出多种新型踝关节康复机器人，如禹润田等[14]设计了一种绳索驱动式并联踝关节康复机构，并对其运动性能进行了分析；KUMAR 等[15]提出了一种分支中含有平行四边形结构的踝关节机器人，建立其运动学模型，分析了机构的可行工作空间区域。

强运动耦合性是一般并联机构的固有特性，尽管这有利于提高机构的刚度和承载能力，但同时也导致其工作空间小、运动学求解复杂和控制设计困难等。而无耦合并联机构除具备一般并联机构精度高、误差小等优点外，其输入和输出运动之间还具有一对一的映射关系，使其运动学、动力学方程非常简单，控制设计也十分容易。因此，对于运动范围较小、低承载的踝关节康复机器人，无耦合转动并联机构具有其自身的优势。

本文基于无耦合RR-RURU两转动并联机构设计出一种新型踝关节康复机器人，该机构仅含有两条分支，结构简单、运动学解耦性好。详细地讨论了机构的运动学、奇异性、工作空间，并对其运动学和动力学特性进行了仿真分析。

1 机构设计与输出特性分析

新型RR-RURU转动并联机构由动平台MP、定平台BP以及连接两平台的两条单开链组成，如图1所示。第一条分支的连接度为6，从定平台到动平台运动副的布置依次为转动副(R11)、万向铰(U12)、转动副(R13)和万向铰(U14)，分支中与同一构件相连的两个转动轴线均相互平行；第二条分支的连接度为2，从定平台到动平台运动副的布置依次为转动副(R21)和转动副(R22)，两转动副轴线垂直且相交。第一条分支U14副中与动平台相连的转轴与第二条分支R22副的轴线相互平行，而安装在定平台上的两转动副R11和R21的轴线相互垂直，选取这两个运动副为主动副。为得到机构特殊的运动学性能，要求第一条分支中R11副与第二条分支中R22副的轴线位于同一平面上，且该平面平行于定平台平面。由于该并联机构中仅含有转动副和万向铰两种类型，故其加工制造成本较低，有较好的经济性。

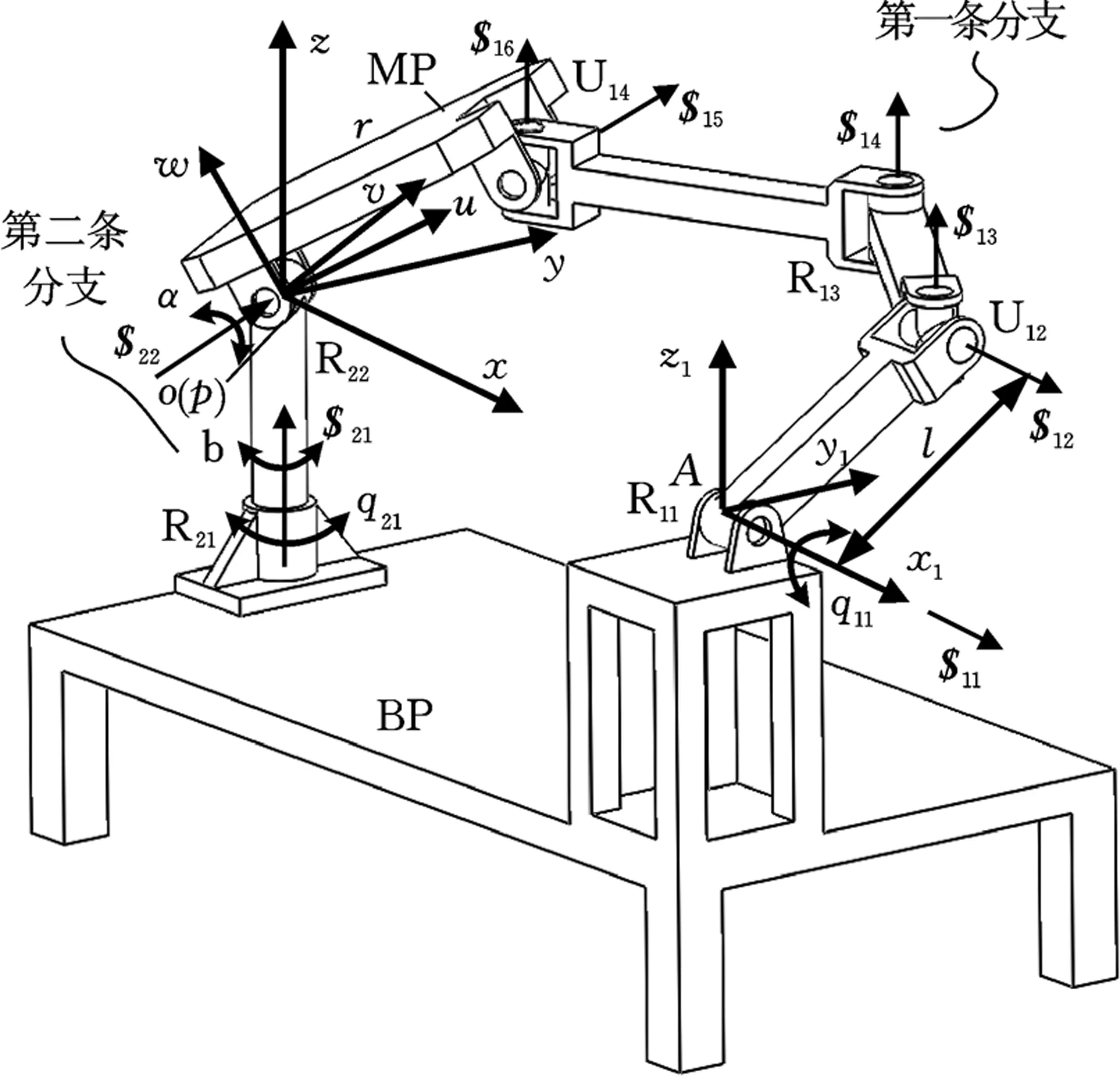
图1 新型RR-RURU转动并联机构Fig.1 Novel RR-RURU rotational parallel mechanism

建立定坐标系oxyz，其原点o位于第二条分支两转动副轴线的交点，z轴与R21副轴线重合，x轴平行于第一条分支的R11副轴线，如图1所示。动坐标系puvw的原点p位于动平台上，且与点o重合，v轴与第二条分支中R22副轴线重合，w轴垂直于动平台平面，u轴可根据右手准则确定。初始位形下，坐标系oxyz和puvw的轴线分别对应重合。设q11和q21分别为两主动副的输入角位移；α为动平台绕v轴转动的姿态角，绕v轴的反方向为正；β为动平台绕z轴转动的姿态角，绕z轴方向为正；l为第一条分支主动杆的长度，即主动副R11轴线到相邻万向铰中心的距离；r表示安装于动平台上的两转轴轴线间的距离。

为便于问题分析，建立局部坐标系Ax1y1z1，其原点A位于第一条分支中与定平台相连的转动副轴线上，且x1轴与该轴线重合，z1轴垂直定平台平面，如图1所示。利用螺旋理论可写出第一条分支运动链的运动螺旋系：

(1)

其中，Pef、Qef、Ref分别为与相应运动螺旋位置相关的参数(e=1,f=4,5,6)。

由式(1)可知，第一条分支的运动螺旋系为6系，故该分支对动平台的运动不提供约束。同理，第二条分支的运动螺旋系为

(2)

即该分支的运动螺旋系为2系，那么其约束螺旋系为4系，由互易积原理得

(3)

式(3)表明，第二条分支的约束螺旋系包含三个轴线相互垂直的约束力和一个轴线垂直于运动副R21和R22轴线所确定平面的约束力偶，即该分支约束了动平台空间内的三个移动自由度和一个垂直于R21和R22轴线所确定平面的转动自由度。由此该新型RR-RURU转动并联机构动平台仅有绕z轴和v轴的转动自由度。同时，由于两分支不存在冗余约束，故该机构为非过约束并联机构。

并联机构的自由度可利用修正Grübler- Kutzbach公式进行计算，即

(4)

其中，M为机构的自由度数，λ为机构的阶数，n为机构的构件总数，g为机构运动副总数；fk为第k个运动副的自由度数；υ为冗余约束数；ζ为局部自由度数。对于图1所示机构，λ=6、n=6、g=6、∑fk=8、υ=0、ζ=0，则该机构的自由度M=6(6-6-1)+8=2。计算结果与前述分析一致，所以该机构只能实现空间二自由度转动。

2 运动学分析

2.1 姿态分析

对于RR-RURU两转动并联机构，其姿态逆解是指已知动平台的姿态角(α和β)，求其主动关节的输入角位移(q11和q21)。

令R为动坐标系相对于定坐标系的姿态变换矩阵，则有

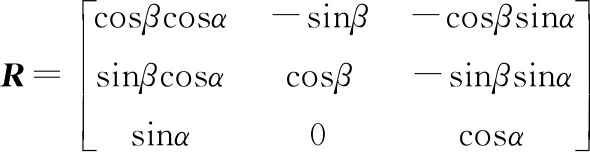
(5)

根据机构的结构特征以及动坐标系的位置，动坐标系的原点p在运动过程中的位移不发生变化，则点p在定系下的位置坐标为(0, 0, 0)T。令动平台上一点m位于第一条分支中万向铰U14的转动中心，它在动坐标系puvw下的向量为mp=(mu，mv，mw)T，那么该点在定坐标系oxyz下的向量mo=(mx，my，mz)T可写为

mo=Rmp

(6)

将式(5)和机构的各结构参数代入式(6)得

mz=rsinα

(7)

根据第一条分支的结构，万向铰U12和U14的转轴中心始终位于同一水平面内，即两者在z轴方向的坐标值相等，由此可得

lsinq11=rsinα

(8)

从而可计算出

(9)

由图1可知，动平台绕z轴的姿态角β仅与第二条分支主动副的角位移q21相关，故两者的关系可写为

q21=β+c0

(10)

式中，c0为动平台绕z轴的初始角度。

由于前文定义了动坐标系在初始位置时与定坐标系重合，即c0=0，那么式(10)可改写为

q21=β

(11)

式(9)和式(11)即机构的姿态逆解方程。将逆解方程作简单变形，可得到机构的姿态正解方程，有

(12)

2.2 角速度分析

将式(8)和式(11)对时间进行一阶求导并整理成矩阵形式，得

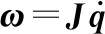
(13)

(14)

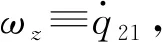
同样，根据式(14)可直接写出动平台绕v轴的角速度与第一条分支主动副输入速度之间的关系，有

(15)

联立式(8)与式(15)得

(16)

其中，角速度传递因子

(17)

式中，d为机构的结构尺寸比例系数,d=l/r。

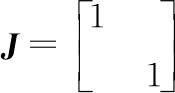
(18)

图2 角速度传递因子g与两自变量之间关系Fig.2 Relationship between the angular velocityg transferring factor and two variable parameters

换言之，当结构尺寸比例系数d=1时，速度雅可比矩阵为2×2阶单位阵，那么条件数和行列式的值必然恒等于1，故此时机构在整个工作空间内都具有完全各向同性的运动学特性。

3 奇异性分析

奇异性是并联机构的固有属性，当机构的结构及尺寸确定时，其奇异位形便随之确定，奇异性分析是并联机构设计中必不可少的环节。从螺旋理论的观点来讲，并联机构运动奇异的发生与分支运动链的运动螺旋系的阶数有关[16]。当运动螺旋系发生改变时，对动平台的约束螺旋系随之变化，导致机构动平台会瞬间得到或失去一个或几个自由度。

由式(2)可知，第二条分支的运动螺旋系始终为2系，由此该分支不存在运动奇异。而由式(1)知第一条分支的运动螺旋系为6系，该螺旋系的相关性可通过该螺旋系构成的6×6阶方阵A是否满秩判定，且有

(19)

当矩阵A的行列式det(A)=0时，该螺旋系线性相关。计算矩阵A行列式的值可得

det(A)=-lcosq11cosβ[Q14(lcosq11-P15)+

Q15(P14-lcosq11)]

(20)

若det(A)=0，则有cosβ=0、cosq11=0或Q14(lcosq11-P15)+Q15(P14-lcosq11)=0三种情况。

(1)cosβ=0。当cosβ=0，即β=±π/2时，在该位形下运动螺旋$11、$12和$16平行共面，3个旋量线性相关，如图3所示。锁定主动运动螺旋$11后，动平台仍可以绕v轴转动，因此，在β=±π/2的位形下，该分支失去对动平台沿z轴移动的约束，如图3所示。值得注意的是，第一条分支失去对动平台的控制后，$13、$14和$15将发生偏转，其轴线不再与z轴平行，从而使得机构动平台失去绕z轴的转动自由度。为避免此种奇异情况的发生，只需将第二条分支的输入角位移限定在适当范围内即可。

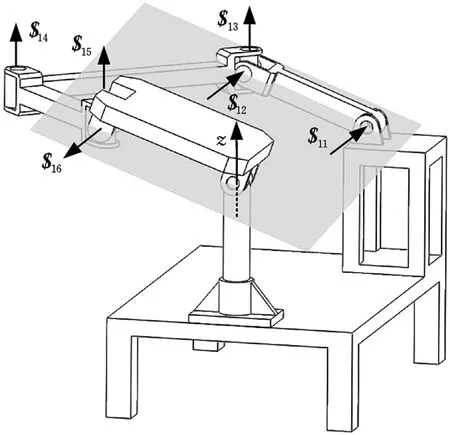
图3 β=π/2时的奇异位形Fig.3 Singular configuration when β=π/2

(2)cosq11=0。此时输入角q11=±π/2，将其代入式(1)可推导出该位形下第一条分支运动螺旋系的约束螺旋，即

(21)

式(21)表明该约束螺旋为平行于z轴的线力矢，约束了第一条分支末端构件沿z轴的移动，从而导致机构动平台无法绕v轴转动。对于图1机构的结构形式，当取q11=-π/2时，第一条分支的主动构件将与定平台产生干涉，故本文机构只存在q11=π/2时的奇异位形，如图4所示。

图4 q11=π/2时的位形Fig.4 Configuration of q11=π/2

(3)Q14(lcosq11-P15)+Q15(P14-lcosq11)=0。当且仅当螺旋$13、$14、$15共面时，才满足上述方程。这种情况发生时，机构有两种位形，即第一条分支的两个连杆处于伸展或重叠状态，如图5所示。但只要合理设计机构的结构尺寸便可避免该奇异的发生。

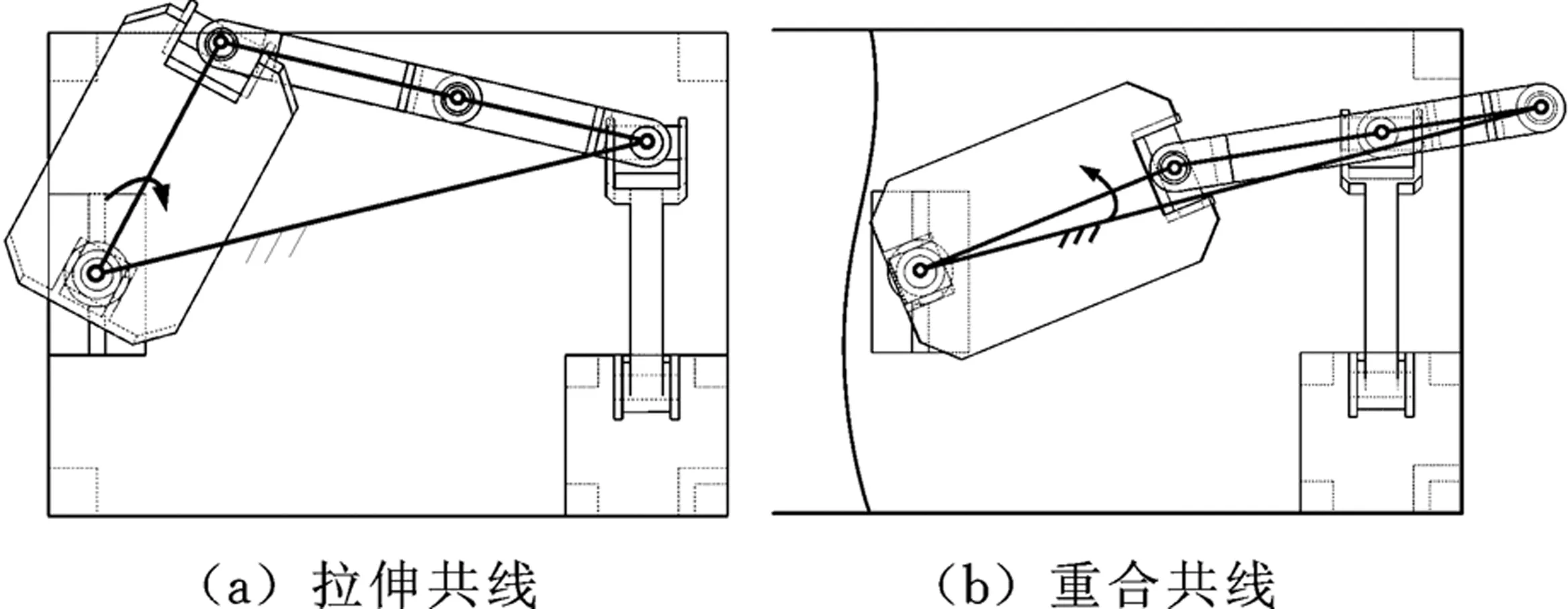
图5 连杆共线奇异位形Fig.5 Coline singular of connecting rod

当然，上述三种奇异情况也可能组合出现，本文不再赘述。

4 工作空间分析

并联机构的工作空间指机构动平台所能达到的工作范围，是衡量机构运动性能的重要指标。根据机构的运动学分析，本文所述的RR-RURU两转动并联机构具有无耦合的运动学特性，即机构动平台的两个转动自由度分别由两个分支单独控制。因此，可采用运动分解的思想对机构的工作空间进行分析。

对于图1所示机构，影响其工作空间的因素主要有机构的奇异位形、万向铰的转角范围，以及连杆间的干涉等。在工作空间分析时，若给定任何一个绕v轴转动的α角，则动平台绕z轴转动的姿态角β的求解可借助于一个“平面四杆机构EDCB”进行，如图6所示。原机构中轴线始终平行于z轴的4个转轴可视为平面四杆机构的4个铰链，动平台为四杆机构的主动构件ED。

图6 分支简化示意图Fig.6 Schematic diagram of limb simplified

根据曲柄存在条件，合理设计图6所示构件长度，可使得动平台绕z轴整周回转。为避免运动过程中发生构件干涉，可将万向铰的十字转轴改为两个独立转轴，如图7所示。设置各构件尺寸分别为l=300 mm、lED=300 mm、lDC=500 mm、lCB=500 mm、lBE=600 mm。

图7 万向铰设计示意图Fig.7 Schematic diagram of universal design

可借助动平台上点m在定坐标系下的向量mo=(mx，my，mz)T来描述动平台在运动过程中的姿态变化，见图1。由式(6)和(12)可得，点m在静坐标系下的位置坐标值与动平台姿态角之间的关系为

(22)

因机构的第一条分支控制了动平台绕v轴的转动，故影响工作空间大小的因素为机构的奇异位形以及连杆与静平台之间的干涉。在球坐标系中绘制出机构动平台的工作空间三维图像，如图8所示，该图像为球面的一部分，坐标系的原点位于其球心处，图中颜色变化表示动平台绕v轴的姿态角α的变化。同时，球面上任意一点即点m的轨迹点，向量mo的姿态角即动平台的姿态角，由此该机构可称为球面并联机构，在仿生关节、雷达天线等需要做定点转动的场合具有潜在的应用前景。

图8 RR-RURU并联机构工作空间Fig.8 Workspace of the RR-RURU parallel mechanism

5 新型踝关节康复机器人运动学和动力学仿真

现有的基于并联机构的踝关节康复机器人装置，其机器人脚踏板(即动平台)的旋转中心通常与患者脚踝的转动中心不重合，导致使用者的小腿在康复训练过程中无法保持静止，而踏板的旋转运动也不一定和小腿与脚之间的相对旋转运动相同，这会增加机器人驱动力实时计算的复杂性。虽然基于外骨骼的设计可以避免上述问题，然而机器人在被安装到使用者身上之前是不能被驱动的，由此外骨骼式机器人的运动学特性并不完全清楚，其控制设计比基于并联机构的康复机器人更具挑战性。

基于RR-RURU两转动并联机构的新型踝关节康复机器人三维CAD模型如图9所示。根据前文分析，该踝关节康复机器人具有无耦合的运动学特性，在控制设计和路径规划方面较为容易。考虑到人体踝关节的结构特征，将RR分支主动副的旋转中心与外展/内收动作的转动中心重合，将RR分支被动转动副的轴线通过患者的跖屈/背屈转动中心。根据踝关节生理要求，康复过程中机器人不仅需要能牵引足部以达到最大偏转角度，还需要能模拟人体正常步态下踝关节的角度变化[17-18]。

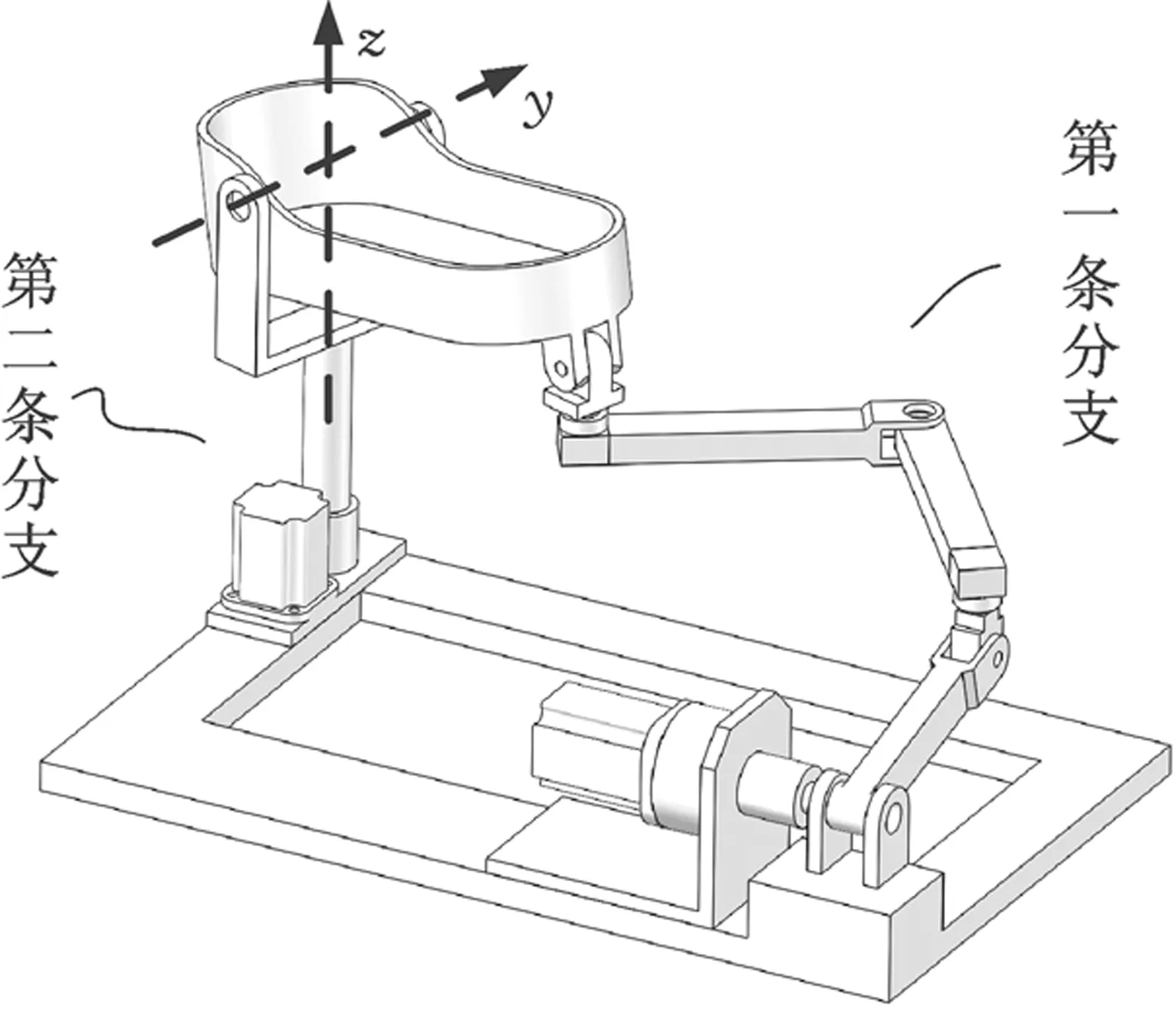
图9 新型踝关节康复机器人Fig.9 A novel ankle rehabilitation robot

根据临床医学步态分析数据[19-21]可得到一个步态周期T内人体踝关节角度拟合曲线，见图10。利用正弦曲线拟合两种角度变化，发现8阶正弦曲线对数据的拟合度最好，其调整自由度复相关系数均达到0.999以上。得到两种角度随时间t变化的函数为

(23)

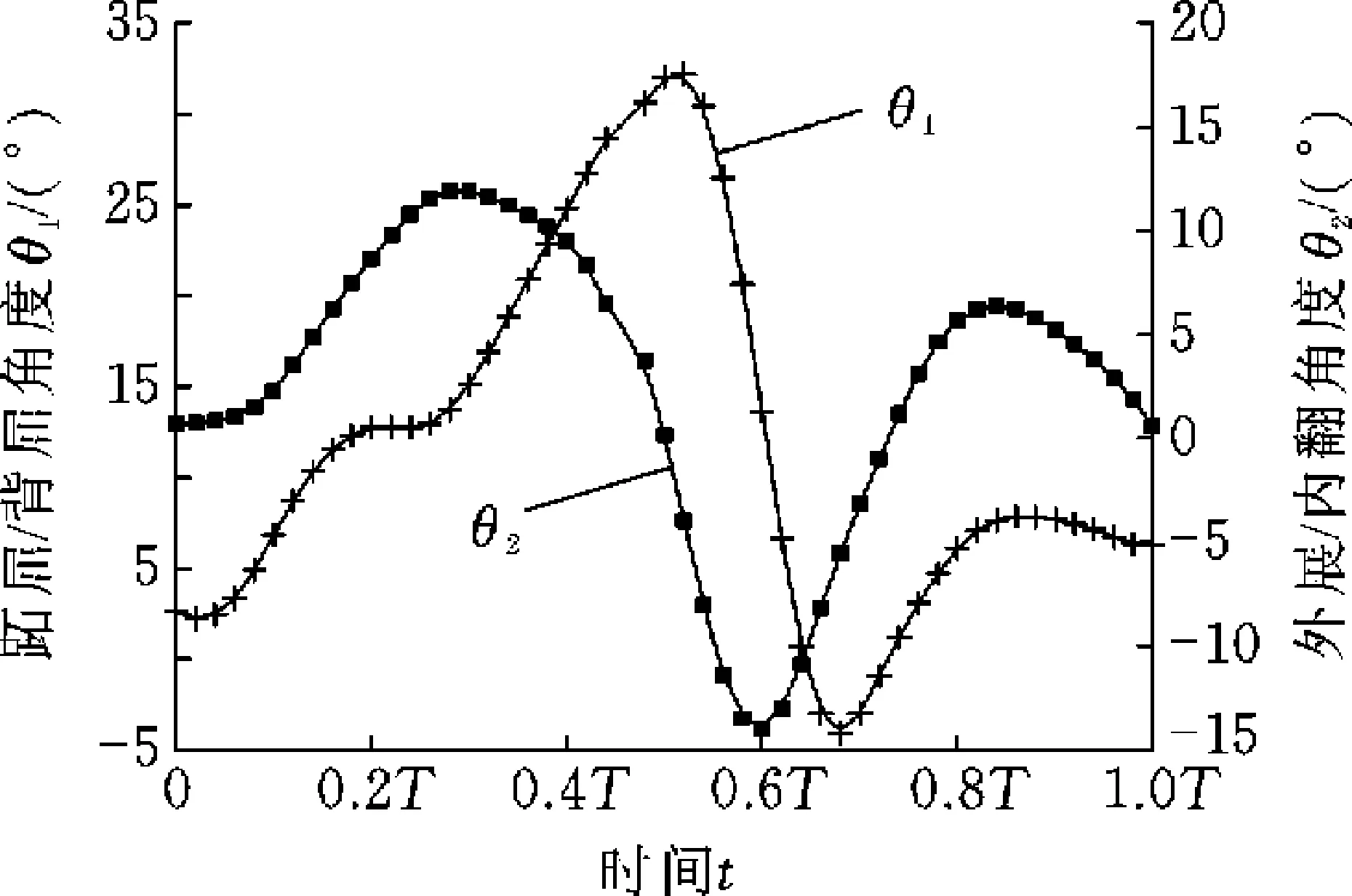
图10 一个步态周期踝关节角度变化Fig.10 Ankle angle change in a gait cycle

其中，aij、bij、cij为常数，下标i表示正弦函数的个数；j=1,2,j=1时表示为跖屈/背屈角度拟合函数，j=2时表示外展/内收角度拟合函数，各参数值见表1。

表1 踝关节角度变化函数参数

由于所设计机器人在满足一定结构尺寸条件下具有完全各向同性的运动学特性，故可直接将一个步态周期内踝关节运动拟合函数分别作为两分支的驱动函数。利用ADAMS软件的运动学仿真模块对该踝关节康复机器人的运动进行仿真，设置杆长系数d=1，仿真时间为100 s，仿真步数为500，得到的仿真曲线见图11。

图11 机器人动平台角位移Fig.11 Angular displacement of the robot platform

对比图10和图11可知，两种仿真曲线几乎完全一致，反映出该踝关节康复机器人能真实地拟合人正常行走时踝关节的角度变化。同时，仿真结果表明，机构的输入-输出运动成一对一的映射关系，两个方向上的运动互不干涉，从而验证了运动学分析的正确性。

踝关节康复机器人的一个重要设计指标是机器人在康复训练过程中对患者脚踝所施加力矩的变化规律能否满足康复要求。就脚的跖屈/背屈运动而言，使踝关节达到最大背屈量30°需要的扭矩为44 N·m，达到最大跖屈量40°需要的扭矩为37 N·m，然而对于外展/内收运动，达到最大外展角度15°和最大内收角度25°所需要的扭矩分别为44 N·m和33 N·m[22]，故踝关节康复机器人的力矩一般要求应不小于50 N·m。

为模拟康复过程中机器人主动关节驱动力矩的变化规律，假定脚踝反作用于机器人踏板上两个方向的阻力矩均为50sin(0.25πt)N·m，控制跖屈/背屈转角的驱动函数为45°sin(0.25πt)，控制外展内收转角的驱动函数为30°sin(0.25πt)。利用ADAMS动力学仿真模块，可对该踝关节康复机器人的动力学性能进行仿真分析，得到的仿真曲线见图12。

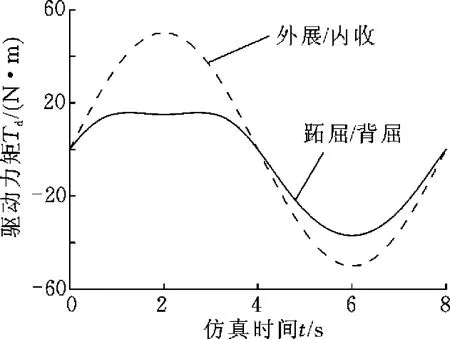
图12 踝关节康复机器人驱动力矩Fig.12 Driving torque for ankle rehabilitation robot

仿真结果初步显示，基于RR-RURU并联机构的踝关节康复机器人在运动过程中驱动力平滑过渡，不存在突变或间断点，具有良好的动力学性能，符合踝关节机器人对于安全性的考虑。

6 结论

(1)本文提出一种新型两转动并联机构，运动学分析显示其速度雅可比矩阵为对角阵，因此该机构具有无耦合的运动学特性。尤其是当机构尺寸比例系数d=1时，雅可比矩阵演化为单位阵，此时机构在整个工作空间内表现为完全各向同性。

(2)基于分支运动螺旋系的奇异性，分析了机构的奇异位形。同时，讨论机构工作空间的影响因素，并绘制出机构的姿态空间。

(3)将该新机构应用于踝关节康复机器人，基于CGA数据对机构运动学进行仿真分析，验证了理论分析的正确性。动力学仿真结果为机器人驱动器的选取提供了依据。