基于形状记忆合金阻尼器的输电塔线体系风振控制

万书亭,程侃如,董 庆,张 雄

(华北电力大学 机械工程系,河北 保定 071003)

输电塔是一种高耸柔性结构,这使得它对动载荷特别是风荷载尤其敏感,容易发生振动疲劳损伤和极端条件下的倒塌破坏,进而影响供电系统的正常运行.对输电塔进行风振控制研究已经成为电力工程界一个重要的研究课题.输电塔风振控制通过改变或调整结构的动力特性、动力作用.减小工程结构振动反应,从而达到对输电塔振动的有效控制.

结构振动控制理论在输电线路中的研究仍处于初期发展阶段,控制方式以被动控制为主,即在输电塔的特定部位装设耗能减振装置来吸收和耗散振动能量,以降低输电塔在风荷载作用下的振动,提高输电塔结构的稳定性,确保其正常工作状态.

在输电塔被动控制中,耗能减振装置通常称为阻尼器,常用的阻尼器有黏弹性阻尼器、金属阻尼器、橡胶铅芯阻尼器等.江宜城等[1]以晋东南-南阳-荆门1 000 kV输电线路中的耐张塔、直线塔为工程背景,采用双层黏弹性材料和铅组合的黏弹性铅芯阻尼器进行风振控制,提出7种布置方案,通过时域内的控制效果分析,得出加设黏弹性铅芯阻尼器后塔顶速度、加速度位移的最大值、均方值均明显减小.陈波等[2]基于半主动摩擦阻尼器的特点,提出了抑制结构风振反应的两种半主动控制策略,通过数值研究得到了半主动摩擦阻尼器可以有效地抑制输电塔的风致振动的结论.尹鹏[3]采用悬挂式调频质量阻尼器对某双钢管塔进行了顺风向风振控制研究,通过调频质量阻尼器参数优化,有效地抑制了塔顶点位移.瞿伟廉[4]建立了输电线塔MR阻尼器半主动风振控制的设计方案,以长沙-岗市湘江输电塔线体系为工程背景,装置10个MR阻尼器,采用4种控制方案对该输电塔的风振反应进行了控制研究.结果表明:半主动控制减振效果最均匀,在保证对位移减振效果的同时速度和加速度的减振效果也有效提高.

虽然这些阻尼器的减振效果明显,但也存在黏弹性阻尼器易老化、金属屈服阻尼器产生塑性屈服后变形很难恢复等缺点.文献[5-6]引入一种新型智能材料——形状记忆合金(Shape Memory Alloy,SMA)制成的被动耗能阻尼器,因SMA所特有的形状记忆、超弹性、大变位、高耗能、良好的耐腐蚀及耐疲劳性能等优势,克服了其他阻尼器存在的老化、塑性形变难以恢复等问题.为了研究SMA阻尼器对输电塔风振控制的效果,本文应用ANSYS有限元仿真模拟了脉动风荷载作用下不同控制方案结构的动力响应,对控制效果进行了对比分析,为SMA阻尼器在输电塔风振控制中的实际应用提供了参考依据.

1 输电塔线体系建模及动特性分析

输电线路的塔-线系统是一个刚柔耦合的非线性系统,其风致振动响应是一个非线性过程.为对输电塔线体系减震方案进行研究,在本文前期研究中,首先使用ANSYS建立了输电塔线体系的模型.

1.1 有限元模型的建立

选择《江苏电网220 kV输电线路标准化设计》中ZA1-ZK1型塔作为研究对象,根据单线图,在ANSYS中构建了输电塔的三维有限元模型,该模型由908个节点、1 430个单元构成.而导地线作为一种柔性的结构,可以把它处理成单悬索.

所建塔-线体系模型为一塔两线模型,由于是单回路,所以共有6根导线和4根地线,其中每根导地线用LINK10模拟,设置为仅受拉,每段导地线划分100段.导地线与绝缘子之间为铰接,另一端施加固定约束.可以得到输电塔线体系的有限元模型如图1所示.

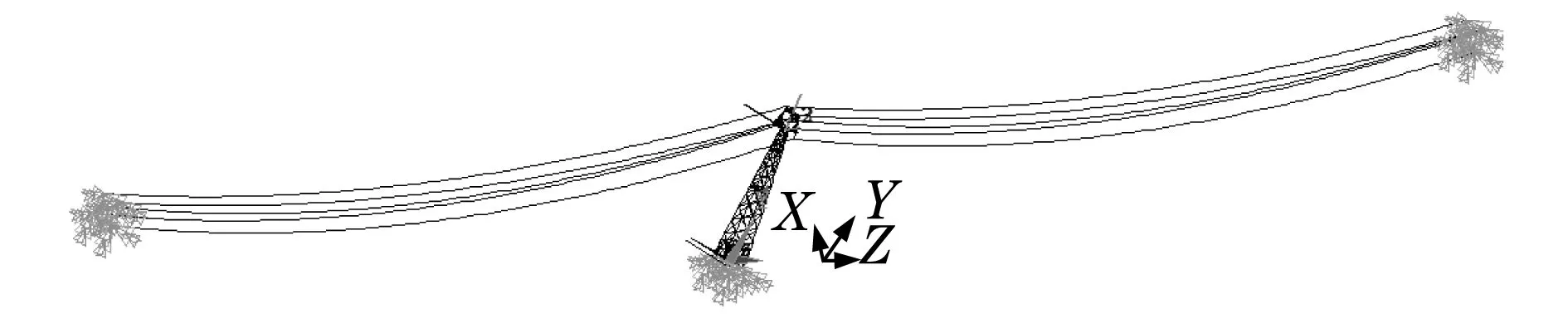
图1 输电线路塔线体系有限元模型Fig.1 Transmission line tower-line system finite element model

1.2 输电塔线体系的动力特性

一般情况下,结构的固有频率和振型受阻尼的影响不大,不考虑阻尼时自由振动方程为

(1)

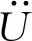
如果结构做简谐振动,则有

(2)

将式(2)带入式(1),计算化简可得到如下齐次方程:

(3)

对输电塔单塔的动力特性进行分析,将塔腿4个接地点进行固定约束,然后进行模态分析,分析其振型和自振频率,并通过模态分析查看铁塔建模中是否存在未约束的杆件.表1列出了单塔的前10阶固有频率和振型描述.图2给出了铁塔具有代表性的几个振型图.

由图2可以看出:1阶和2阶模态均为弯曲模态,导致两个方向的弯曲的原因是塔头部位铁塔的构造在顺线路方向和横线路方向不同.3阶到6阶模态主要为塔腿处的局部模态,原因是塔腿处的杆件之间的约束强度不如塔体和塔头,所以会率先体现在模态振型之中.7阶、8阶、9阶模态为顺线路方向的2阶弯曲、横线路方向的2阶弯曲和2阶扭转模态,这与文献[7]的研究结果也类似,间接证明了该输电塔模型的正确性.

图2 单塔振型图Fig.2 Single tower vibration pattern

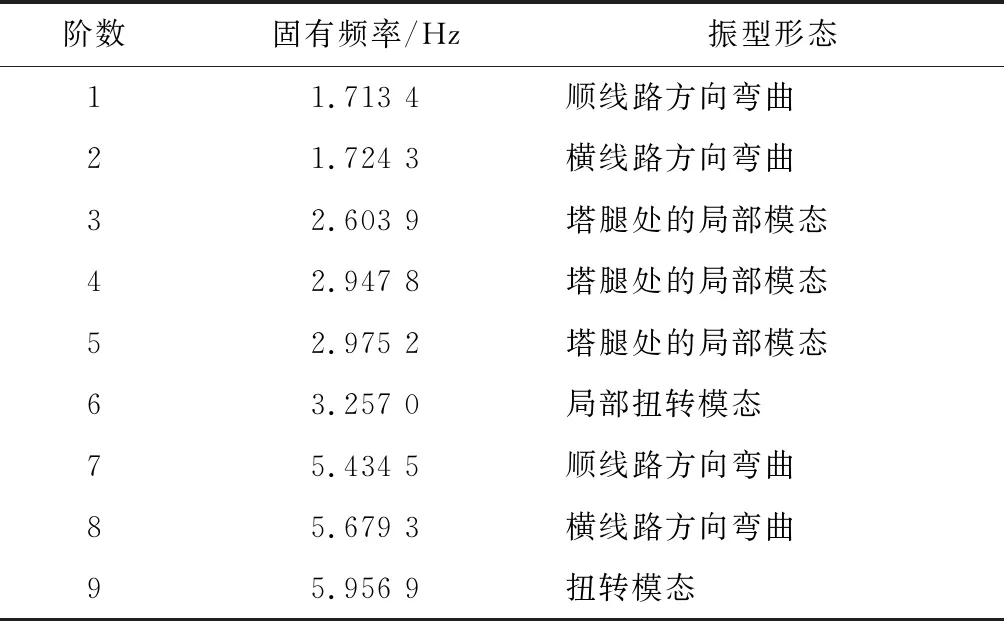
表1 单塔的前9振型和固有频率Tab.1 Single tower’s front 9 mode shape and natural frequency

输电线路塔线体系是一组耦合体系,单独研究输电塔和导线的动力特性不能准确地揭示真实的输电线路塔线体系的动力特性,所以需要研究输电塔和导线之间的相互影响,对整个输电线路塔线体系进行动力特性分析[7-8].此外,如果只考虑输电塔而忽略导地线对输电塔的影响以及塔线之间的相互影响,缺乏对输电线路塔线体系的动力特性认识,在这样的基础上进行的减振策略研究分析是不符合实际情况的,故下面将对整个塔线体系进行动力特性分析.表2为输电线路塔线体系的模态求解结果的前9阶.

对比分析单塔时的前9阶模态,可以明显看出:除第2阶外,塔线体系的前9阶固有频率均比单塔时要小一些.这是因为导地线作为柔性结构,导致整个结构的刚度变小.由此可知,导地线对输电铁塔的振动特性有明显的影响,在对输电铁塔进行减振策略分析时必须考虑导地线的影响,并在建模时连同导地线一同建立塔线体系模型.

表2 塔线体系的模态Tab.2 Tower mode modality

图3为输电线路塔线体系的前两阶振型.

图3 输电线路塔线体系的前两阶振型Fig.3 The first two modes of the transmission line tower line system

从图3中可以看出:塔线体系的前两阶振型与单塔时一致,第1阶为横线路方向的弯曲振型,第2阶为顺线路方向的弯曲振型.

2 脉动风速时程和风载荷时程的数值模拟

2.1 脉动风速时程的模拟研究

利用谐波合成法模拟单个脉动风速时程:

(4)

式中:N为频率的分段数;S(ωn)为脉动风速功率谱的表达式;ωn采用圆频率;Δω为频率步长,其值等于频率上限ωp减去频率下限ωl除以频率分段数N;n为频率序列数;Φn=ωl+(2n-1)Δω/2为随机的相位角,取值范围为0～2π.

对于n个空间相关的脉动风速,其互功率谱密度函数矩阵为

(5)

运用Cholesky分解,可将S(ω)分解为

(6)

式中：

(7)

第i个脉动风速的表达式为

(8)

式中:

(9)

θjm(ωml)为两个不同位置的点之间的相位角,按照如下公式进行计算：

(10)

当模拟的风为均匀湍流时,θjm(ωml)的值为0,θml的值取0到2π之间的随机值.

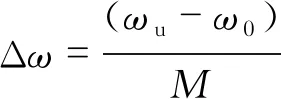
(11)

式中:N≥2M,取整数.

选定恰当的参数即可对风速时程进行模拟,由于Matlab可以方便地实现Cholesky分解和快速傅里叶变换,故采用Matlab进行模拟.

2.2 塔线体系脉动风速时程模拟

对输电塔和导地线进行分段,每一段模拟一个风速时程,将风速时程转换成风载荷后均分到几个节点加载.其中,输电塔共分为20段进行模拟加载,每段取中间位置的高度为模拟点,计算出载荷除以4后均匀加载在该段上面和下面的共4个节点上,迎风面和背风面同时施加,加载位置如图4所示.

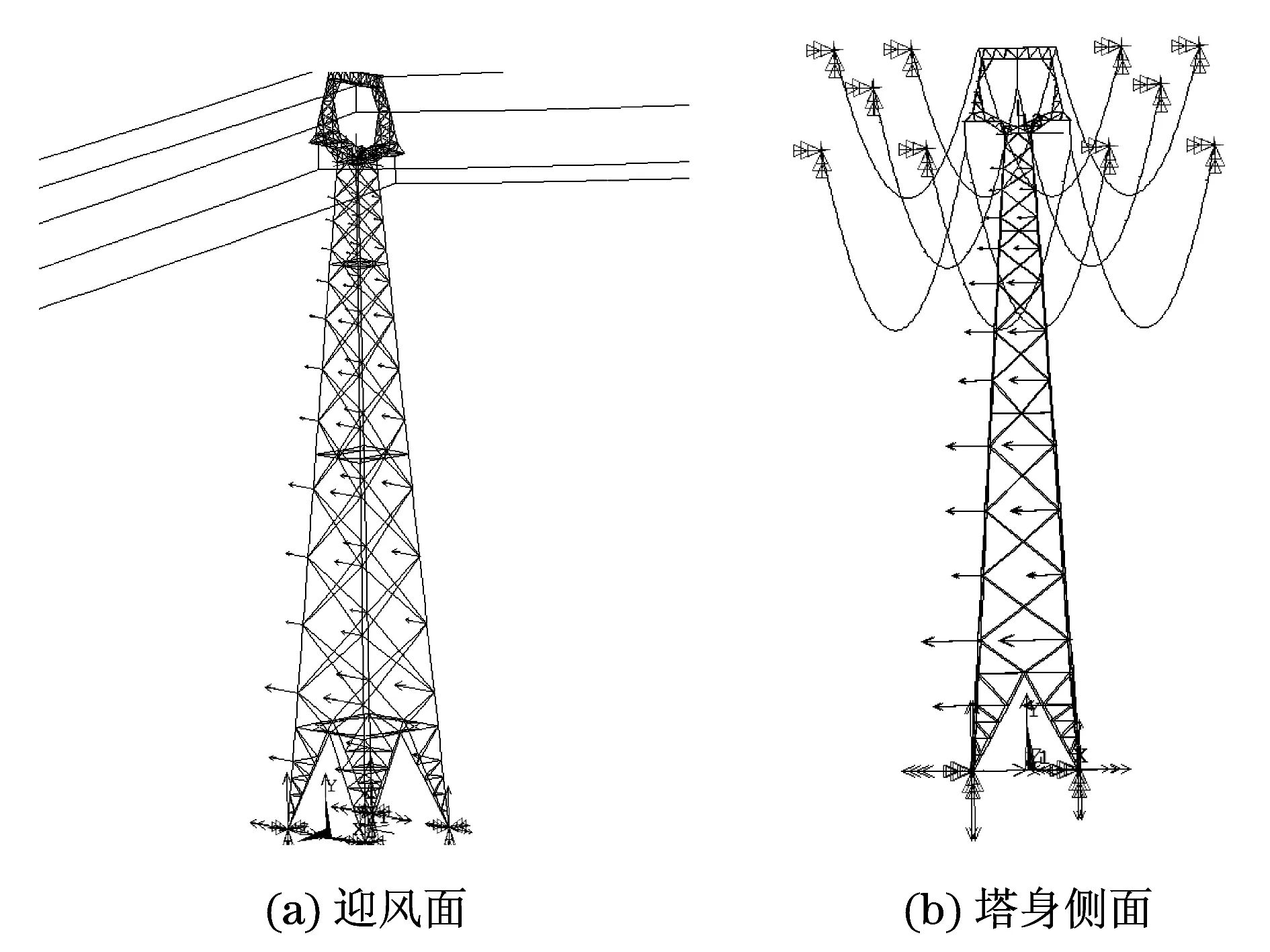
图4 输电塔风载荷加载点Fig.4 Transmission tower wind load loading point

其中投影面积的计算按照如下公式:

(12)

式中:h为区段的竖直高度;φ为铁塔构架的填充系数,按经验塔身部分可以取0.15～0.20,塔头部分取0.30,考虑到节点板挡风面积的作用,应在此基础上乘以风压增大系数,取1.10;b1,b2为区段的上部宽度和下部宽度.

故塔身部分的填充系数可以取0.22,塔头部分的填充系数可以取0.33.导地线部分都均匀划分为10段,具体位置如图5所示.

图5 导地线风速时程模拟点及风载荷加载点Fig.5 Geodetic wind time simulation point and wind load loading point

根据上述研究和参考《江苏电网220 kV输电线路标准化设计》,可得风速时程模拟的相关参数如下:基本风速为28 m/s,B类场地,上截止频率为16π,频率等分数位1 024,模拟点数为2 048,时间步长取0.05 s,输电铁塔模拟点数为20个,导地线的模拟点数为100个,共120个风速时程模拟点.现选取其中几个模拟点的风速时程如图6所示.

3 输电线路塔线体系减震策略

3.1 SMA阻尼器

SMA是一种变形后可以恢复原来形状的金属合金.它具有抗腐蚀性、超弹性、抗疲劳、形状记忆效应和迟滞特性[9-10].

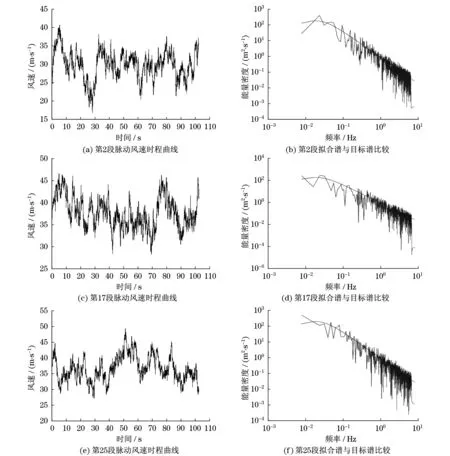
图6 模拟点的风速时程模拟结果Fig.6 Wind speed simulation results of simulation points

利用SMA的超弹性及高阻尼性制成的被动耗能阻尼器,可以克服其他阻尼器面临的老化、可靠性、维护及残余变形等问题,且目前已有将SMA阻尼器应用于框架结构、桥梁等振动控制,其减振效果明显[11-14].

要在ANSYS中模拟SMA的超弹性,需要通过TB,SMA命令的SUPE选项对数据表进行初始化.通过MP命令定义在奥氏体状态下的弹性特性.呈现超弹性的SMA由6个常数进行设置,它们定义了单轴应力状态下加载和卸载的应力-应变行为.对于每个数据集,通过TBTEMP定义温度,然后通过TBDATA定义常数C1～C6,可以以这种方式设置多达99组与温度相关的常数.定义超弹性常数C1～C6的含义如表3所示.

在ANSYS中,支持SMA本构模型的单元类型有很多,包括多种面单元、管单元、实体单元和梁单元,本文选用支持SMA的梁单元中的BEAM188.

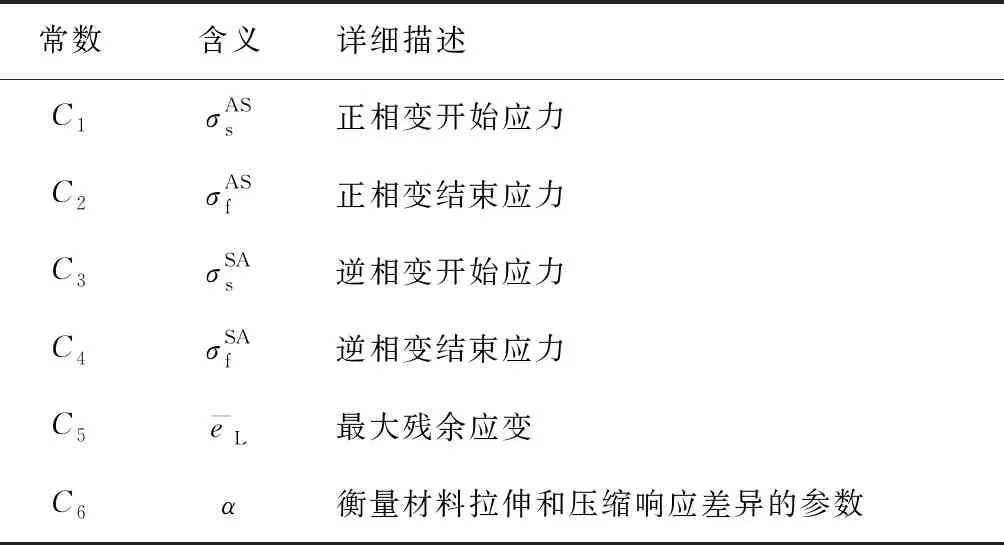
表3 超弹性设置常数Tab.3 Hyperelastic setting constant

3.2 阻尼器布置方案

形状记忆合金阻尼器属于位移阻尼器,根据位移阻尼器的工作原理,在布置时应选择输电塔结构中将会产生较大相对位移的位置.设计以下3种方案:方案1为布置横担与塔身上部主材之间;方案2为交叉布置在塔身中上部;方案3为竖直布置在塔身中上部.布置方案如图7所示.

图7 形状记忆合金阻尼器布置方案(单位：mm)Fig.7 Shape memory alloy damper arrangement scheme (unit：mm)

分别对无阻尼器时和按上述几种方案布置阻尼器的输电线路塔线体系进行瞬态动力学时程分析,查看输电铁塔各部位节点的位移和加速度时程曲线,并通过统计方法计算各部位的减振率,对比即可得到阻尼器布置的最优方案.

3.3 减震效果对比

对输电塔施加模拟的90°风载荷,瞬态动力学的时间步与风载荷模拟时的时间步保持一致,都为0.05 s.均匀选取输电塔迎风面和背风面共366个点进行加载.为了对3种方案的减振效果进行量化,现引入减振率δ这一参数,其计算方法如下:

(13)

式中:R0为无阻尼器时结构的响应;R1为有阻尼器时结构的响应.对塔头部位节点的平均位移、最大位移、平均加速度及最大加速度时程数据进行处理，如表4所示.

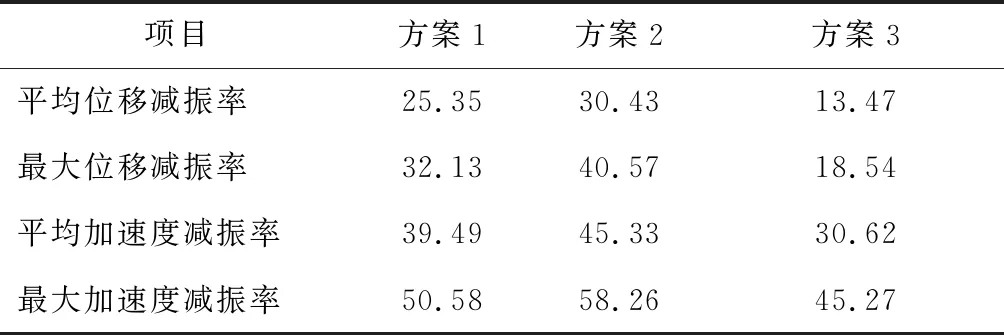
表4 塔头节点减振率Tab.4 Tower top node damping rate %

从表4可以看出:无论是位移减振率还是加速度减振率,方案2都有明显的优势,方案1次之,而方案3最差;加速度减振率明显大于位移减振率,说明阻尼器在降低加速度的效果上明显优于降低位移的效果.

对铁塔不同高度节点的位移时程数据进行处理,可以得到3种方案沿塔高方向的位移减振率,如表5所示.

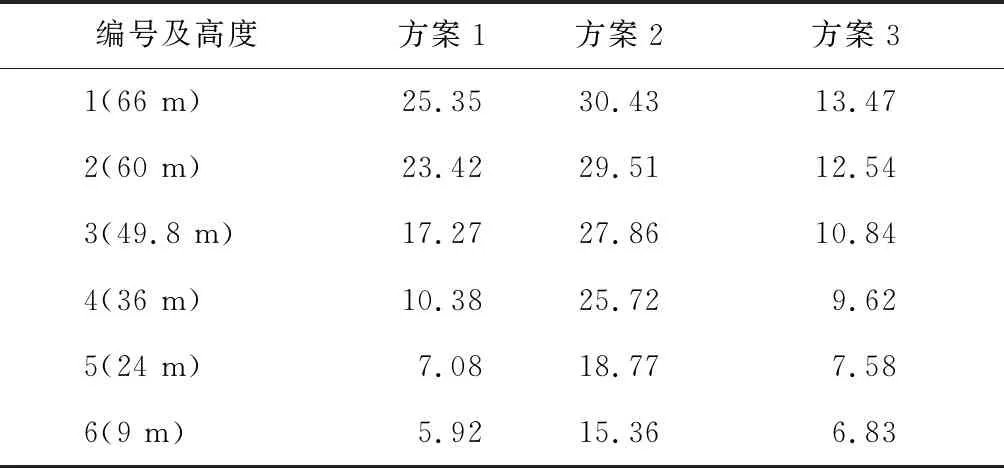
表5 沿塔高方向平均位移减振率Tab.5 Mean displacement damping rate along tower height %

为了更明显地反映减振率的变化情况,绘制折线图如图10所示.

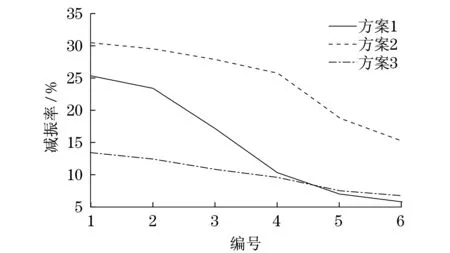
图8 沿塔高方向平均位移减振率Fig.8 Mean displacement damping rate along tower height

通过分析可以得到如下结论:

(1) 在3种方案中,方案2具有最佳的减震效果,且远优于其他两种方案.

(2) 位移减振率随节点高度的增加而增加,导致这种现象的可能原因为:阻尼器的安装位置都在铁塔中部靠上的部位;塔底部的角钢多是Q345钢,而塔上部角钢大多是Q235钢,且底部角钢尺寸大,顶部角钢尺寸小,塔底的刚度远大于塔顶,SMA阻尼器的效果对塔底的影响较小.

(3) 方案1对塔顶的减振效果远大于对塔底的减振效果,这是因为阻尼器只布置在塔头横担与塔身上部主材之间.

(4) 方案3减振效果相对其他两个方案较弱,原因是阻尼器的布置方向为竖直方向,而铁塔在竖直方向的相对位移较小,阻尼器的行程小,耗散的能量少.

4 结语

本文利用ANSYS建立输电线路塔线体系模型并研究了其动力特性,模拟了脉动风速时程和计算了风载荷时程,研究了SMA的特性及SMA阻尼器的数值模拟方法,设计了几种阻尼器布置方案,并通过时程分析得出了优化布置方案.本文分别对无阻尼器的塔线体系和按照上述几种方案布置SMA阻尼器后的塔线体系进行了风荷载时程分析,提取了输电铁塔有代表性的位置处节点的位移和加速度时程曲线,并计算了几种布置方案的减振率.最后，通过对比,选出了最优的阻尼器布置方案.