利用视频分析软件和分析天平改进落球法测液体黏度
郑林静,吴 锋,孟丽娟
(盐城工学院 a.海洋与生物工程学院;b.数理学院,江苏 盐城 224051)
液体黏度的研究在水利、医疗和化工等领域有着广泛的应用价值[1-2]. 实验室中,落球法是测定液体黏度的最常用方法,测量黏度的公式为
(1)
其中,ρ为小球密度,ρ0为液体密度,g为当地重力加速度,d为小球直径,v为小球的终极速度,m为小球质量,r为小球半径. 由不确定度传递公式可知,η的误差主要来自ρ0,v,m和ρ等的测量.
针对ρ0和ρ的测量误差,文献[3]通过引入与小球同材质的大物体,提高了ρ0/ρ的测量精度,改善了液体黏度的测量精度. 然而,改进后的落球法仍存在不足:一是利用目视手动方法测量v,另一个是利用物理天平测量小球质量. 针对v的测量误差较大,文献[4]利用视频分析法代替目视手动方法,提高了v的测量精度. 本文结合文献[3]和文献[4]的优点,并改用分析天平称量物体质量,确定液体黏度. 由此测得蓖麻油的黏度,与标准值吻合,而且精度比传统落球法的结果提高了近1个数量级.
1 实验原理和方法
1.1 改进的落球法
由式(1)有
(2)
式中,m的测量采用舜宇恒平FA2004电子分析天平(量程200 g,分度值0.1 mg),ρ0/ρ的测量转换为与小球同材质的大球质量mB及相关物体质量的测量[3,5]——先用分析天平称出mB和盛有适量待测液体后的烧杯质量m1,然后再称出大球悬没于该烧杯中液体后(见图1左图,轻质细线一端粘着大球并悬没于待测液体中,细线另一端系于固定在分析天平顶盖内侧中心的无粘挂钩上)烧杯的质量m2,则
ρ0=(m2-m1)/VB,
ρ0/ρ=(m2-m1)/mB,
所以
(3)
其中VB为大球的体积.
考虑容器的几何因素对斯托克斯公式的影响,式(3)修正为[6]
(4)
式中,D为容器内径,H为液柱深度.
考虑液体的运动状态对斯托克斯公式的影响,在雷诺数Re(取为ρ0vd/η1)较小时,式(4)进一步修正为[7-8]
(5)
式中1 280在一些文献中被误写为1 080.

图1 实验装置图
1.2 视频分析法确定小球的终极速度
将智能手机(拍摄帧率为30 s-1,图像分辨率为1 920×1 080)安置于三脚架上. 为确保拍摄质量,调节手机摄像头的拍摄焦平面与容器内液柱中心轴线平行,调节三脚架使手机摄像头对准容器中待测液体中部,同时与容器保持适当距离避免视差. 接着在容器顶部安置中心开孔的小盖子以控制小球沿轴线下落. 为给视频分析提供长
度标度,利用铁架台、十字夹和万用夹在容器管壁紧贴固定厘米刻度钢尺,并使该尺平面通过容器内液柱中心轴线(见图1). 为避免手动操作导致手机拍摄面的抖动,用与三脚架相配套的蓝牙遥控控制手机拍摄. 最后,利用视频分析软件Tracker[4]实时追踪小球的位置,并由内置的最小二乘拟合功能得到小球的终极速度v.
2 测量结果和分析
选用同一型号精密不锈钢球作为落球测量蓖麻油(分析纯)的黏度,所有物体的质量用上述电子分析天平(仪器允差与具体称量的物体质量占量程的比例有关,取值参见文献[9])称量. 容器内径D=63.94 mm,容器中油深H=39.00 cm,油温T=24.92 ℃,大球直径dB=25.07 mm,所在地区重力加速度[10]g=9.795 9 m/s2. 考虑到实际测量中一般用到多个小球,通过螺旋测微器随机测量6粒不同小球的直径(见表1)得到单个小球的直径d=(2.494±0.003) mm;随机测量6粒不同小球的质量,得到单个小球质量m=(65.97±0.56) mg. 此外,由表1数据还得,mB=(64.919±0.001) g,m1=(151.592±0.001) g,m2=(159.446±0.002) g.
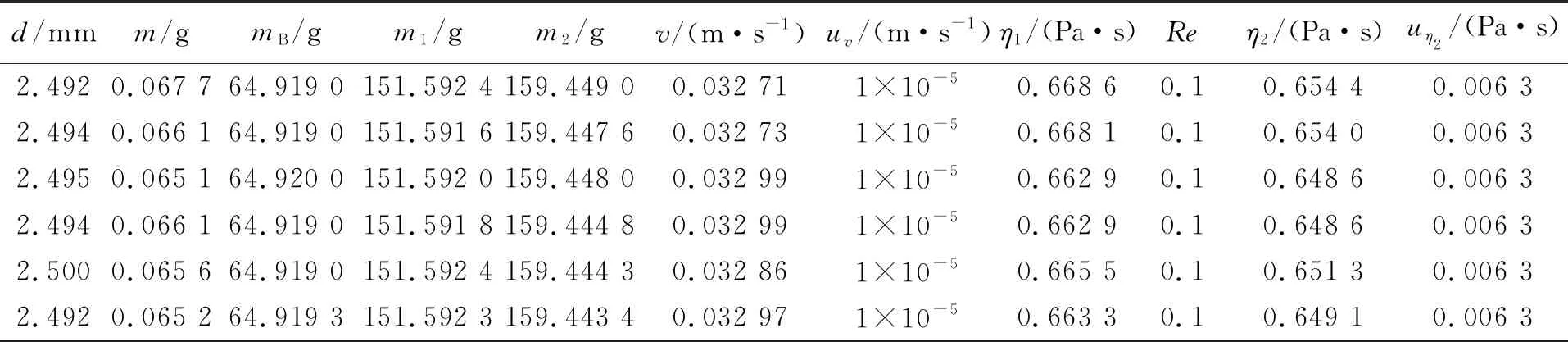
表1 小球的直径和质量等测量数据和结果
为确定小球下落(测6次)的终极速度v,先用Tracker软件绘制出小球在蓖麻油中下落的速度-时间曲线[如图2(a)所示],根据曲线确定小球匀速下落的时间段,再对小球在该时间段内的位移x-时间t进行线性最小二乘拟合[如图2(b)所示],从而得到v及其不确定度uv(表1). 这里计算出的uv只考虑了随机误差,所以uv的数值只反映了在v的测量中随机误差很小. 注意到6次测量的v值间差异达到1×10-4m/s,这说明测量v时还存在确定性误差(例如相机感光相元尺寸对位置测量精度的限制,帧频和曝光时间对时间测量精度的限制),所以v的测量值只有3位有效数字. 由于小球直径/半径的测量值有4位有效数字,结合式(3)可知,小球质量的测量值至少应该有3位有效数字,而使用物理天平测量小球质量达不到3位有效数字,进而成为限制测量精度提高的主要因素,所以利用精度更高的分析天平测量小球质量十分必要.
现将计算出的v代入式(4),算出蓖麻油黏度η1及雷诺数Re. 由于Re=0.1非常小,仅考虑容器几何效应得到的η1已与标准值0.658 4 Pa·s(根据文献[11]的实验数据拟合出的公式η=5.529 2e-0.085 390 T计算)相当吻合. 若再对η1进行雷诺数修正到二级近似,那么由此确定的蓖麻油黏度η2已足够准确.
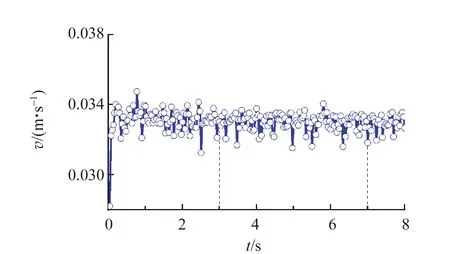
(a)速度-时间曲线

(b)匀速段位移随时间的变化及其线性拟合结果图2 第3次测量时小球下落的速度和位移
根据不确定度传递公式计算η2的不确定度uη2. 若直接计算,过程比较复杂,但是因为Re很小且d≪D,d≪H,所以uη2≈uη. 计算可得,6次测量中η2的相对误差为0.96%或0.97%. 作为对比,使用目视手动方法测量了上述6次小球下落终极速度,得到η2=(0.676±0.017) Pa·s,相对误差为2.4%. 可见,融入视频分析法改进后,落球法测量结果的相对误差减小为目视手动测量结果的2/5.
3 讨 论
对利用分析天平代替物理天平称量小球质量的原因和意义进一步剖析. 文献[3]结合物理天平对传统落球法进行了改进,提高了黏度的测量精度. 经计算分析发现,文献[3]中小球质量的测量误差是限制液体黏度精度大幅提高的主要因素. 如果小球质量的测量不确定度减小为原来的1/10,那么由文献[3]改进的落球法得到的黏度的相对误差将减小为原来的1/3. 所以使用分析天平称量小球质量能大幅度降低小球质量的测量误差,提高液体黏度的测量精度. 如果进一步融入视频分析法来测量液体黏度,那么可以估算,所得液体黏度的相对误差约为传统落球法的2/15. 也就是说,液体黏度的测量精度将比传统落球法的精度提高了近一个数量级.
4 结束语
结合文献[3]和文献[4]的方法改进落球法测量液体黏度后,限制测量精度的主要因素就变为小球质量的测量. 为使小球质量的测量精度与小球直径和终极速度的相当,应该采用精度更高的分析天平来测量. 测量结果表明,所得液体黏度的精度得到提升. 将物理分析与视频分析相结合的模式,对挖掘物理实验的内涵和培养学生的实践创新能力都有参考价值.

