波耳共振仪数据可视化与精确化探究

陈俊宇,董国波,刘少华,李朝荣,李 华

(北京航空航天大学 a.机械工程及自动化学院；b.物理科学与核能工程学院;c.宇航学院，北京 100191)

波耳共振仪是用来定量研究机械振动的仪器，利用波耳共振仪可以研究自由振动、阻尼振动、受迫振动的幅频特性和相频特性[1-2]. 在信息时代，各类实验仪器朝着可视化、精确化的方向发展[3]，可视化能够直观地让实验者看到现象，精确化可以使更多细节在实验结果中展示出来，因而更容易发现其中的规律，尤其是在波耳共振仪的实验中，存在混沌现象[4]，使用振动图像有助于进一步研究其中的混沌现象[5]. 波耳共振仪的原始数据显示界面比较简单，只能显示出摆轮运动的周期和振幅，而摆轮的实时位置信息和角速度无法测量，不能满足进一步研究阻尼振动和受迫振动的需要. 针对传统波耳共振仪的不足，文献[6]进行了改进，使用了光电门和单片机采集数据. 然而，由于光电门的局限性，不能实时测得摆轮的位置与速度；而且采样频率仍然较低，数据不够精确. 另外，文献[7-8]提出使用鼠标贴附在摆轮表面采集数据的方法，但是鼠标精度低，存在误差积累，导致实际的平衡位置点在图像上漂移，数据失真严重；鼠标传回计算机的数据只能单纯记录鼠标轨迹，在相应软件中绘图，不能导出数据进行进一步研究. 根据编码器原理[9-10]在原有波耳共振仪的基础上添加单片机和增量式光电编码器，可以准确得到摆轮实时位置信息和角速度的大小，记录振动信息的数据导出后可以进行进一步数据处理，从而实现精确化与可视化，使现有波耳共振仪的性能得到提升，满足现代仪器的使用需求.

1 实验原理及装置

波耳共振仪由电机通过连杆机构提供受迫力，由带铁芯的线圈提供阻尼力，由光电门记录振幅和周期. 原始仪器使用2个型号为GZ-6C的光电门来记录周期和振幅，每个光电门包含1路发射器和1路接收器，发射器一侧发射红外信号，接收器一侧接收红外信号. 当光电门中间没有被遮挡时，输出高电平信号；有遮挡时输出低电平信号. 摆轮边缘有均匀分布的180个短凹槽和1个长凹槽. 上方的1对发射器和接收器正对短凹槽的位置，能够在实验中记录转过的短凹槽的个数；下方的1对发射器和接收器正对长凹槽的位置，能够在实验中记录长凹槽经过光电门中心位置的时间，通过2次时间做差是半个周期，乘以2倍可求出周期[11]. 在半个周期的时间内，记录到转过的短凹槽个数即为振幅. 原实验仪器只能测出振动的周期和振幅，不能获得某一时刻的角位移、角速度等振动信息，存在不精确的缺点. 另外，原有的实验仪器无法将完整的角位移-时间曲线呈现出来，存在不直观的缺点.

改进后的实验仪器使用增量式光电编码器记录振幅和周期，增量式光电编码器是通过光电转换原理将输出轴的角位移量转换为脉冲的传感器. 码盘与摆轮同轴致使摆轮的旋转带动码盘旋转，当光电编码器的轴转动时，2个光电检测装置A和B产生脉冲输出，两相脉冲相差90°相位角. 比较两相脉冲的相位可判断转向(如果A相脉冲比B相脉冲超前，则光电编码器为正转，否则为反转)；记录输出脉冲的个数可换算成转过的角度[12-13]. 增量式光电编码器精度高，集成度高，受外界干扰小，输出稳定. 实验中使用的光电编码器型号为OMRON E6B2-CWZ3E，精度为1 000线，即转1周时单相输出1 000个上升沿.

使用STM32F103作为嵌入式控制器. 该单片机的定时器含有编码器模式[14]，能对输入信号进行滤波，从而稳定计数. 在该模式下，单片机将编码器返回的脉冲信息进行硬件四倍频，即编码器转1周单片机会读取4 000个跳变沿. 而对于原始仪器，摆轮转1周，读取振幅的光电门仅产生360个跳变沿，相比于原仪器，改进后的测量精度提升约为11倍(4 000/360).

记录摆轮的实时位置采用了变M法测速的方法[15]. 在实验开始前将记录脉冲数的寄存器清零. 实验时使用定时器中断，每隔10 ms记录读取到的脉冲数，利用脉冲数与角度的对应关系，将脉冲数换算成角度后通过串口输出到计算机，然后将记录脉冲数的寄存器清零.

编码器与摆轮同心安装，如图1所示. 在摆轮轴承处原本有1个挡片，通过3颗螺钉与摆轮连接. 拆下挡片后，换上3D打印的连接件，该连接件与原来的挡片相比多1根轴，可以通过联轴器将这个轴与编码器轴相连. 使用激光切割机对

图1 编码器安装

椴木层板进行加工，经插接和粘接后制成编码器支架，使用螺钉将编码器与支架相连.

编码器输出的AB两相分别与TIM5的通道1和通道2相连，使用编码器模式. 单片机与电脑相连，通过串口传输数据.

2 实验结果

2.1 曲线绘制

单片机每隔10 ms实时地向电脑返回摆轮的位置和时间信息，计算机通过SerialChart软件进行处理，可以绘制出实时的角位移-时间曲线. 将接收到的数据导入Excel中，可以精确地绘制多种图像.

图2～4为3种阻尼下阻尼振动振幅θ-时间t曲线，图5为阻尼1挡条件拟合曲线局部. 可以直观地看到，随着阻尼1，2和3挡递增，振动的总时间依次递减.

振动曲线的细节对比如图6所示. 如果不使用编码器，就不能精确记录振动信息，这种细微的差异很难在实验中直观感受到.

图2 阻尼1挡条件拟合曲线

图3 阻尼2挡条件拟合曲线

图4 阻尼3挡条件拟合曲线

图5 阻尼1挡条件拟合曲线局部

图6 不同阻尼条件下阻尼振动振幅-时间曲线对比(局部)

用相邻时间间隔测得的角位移之差除以单位时间(10 ms)，可以得到角速度. 以摆轮摆动角度θ为横轴，摆轮摆动角速度ω为纵轴，绘制出振动相图，可以用于研究混沌现象.

图7 自由振动和阻尼1挡时的振动相图

图8 自由振动和阻尼1挡时的振动相图(局部)

图7和图8比较了自由振动和1挡阻尼时的振动相图，二者最终都收敛于角位移为0、角速度为0的点，说明这点处于振动的平衡状态. 自由振动相图较密而阻尼振动相图较疏，说明阻尼振动更快趋向于平衡.

2.2 效果分析

相比于原始的波耳共振仪只能测量周期和振幅，使用编码器改进后，不仅能测量周期和振幅，还可以测量位置与速度信息，绘制实时的振动曲线，使数据呈现方式更加直观，有助于对振动的理解. 原始波耳共振仪的分辨率是360°/360=1°，而使用编码器改进后分辨率提升为360°/4 000=0.09°，数据更加精确. 此外，改进所用的费用低廉，可以取代原始仪器机箱中测量周期和振幅的部分.

3 编码器外部引入阻尼的影响分析

为了分析编码器引入的外部阻尼对于阻尼系数的影响，不妨假设编码器所引入的阻尼类似于仪器自带的电磁阻尼(阻尼与角速度成正比). 分别测量并计算无编码器和有编码器2种条件下的摆轮做系列阻尼振动和自由振动时的阻尼系数.

当摆轮在有摩擦阻尼和电磁阻尼的媒质中运动时，其运动方程为[16-17]

(1)

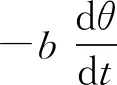
(2)

当mcos (ωt)=0时，式(2)即为阻尼振动方程. 当β=0即在无阻尼情况时,式(2)变为简谐运动方程，系统的固有频率为ω0. 式(2)的通解为

θ=θ0e-β tcos (ω0t+α),

(3)

设t1时刻

cos (ωt1+α)=1,

(4)

记

θ1=θ0e-β t1.

(5)

设tn时刻

cos [ω(t1+nT)+α]=1,

(6)

记

θn=θ0e-β tn=θ0e-β(t1+nT).

(7)

由式(5)与式(7)得

(8)

等式两边取对数得

(9)

取5组数据进行逐差法计算：

(10)

(11)

多组实验结果求取平均值得到最终表数阻尼系数的表达式为

(12)

代入测得的数值计算可得表1中各种情况下的阻尼系数.

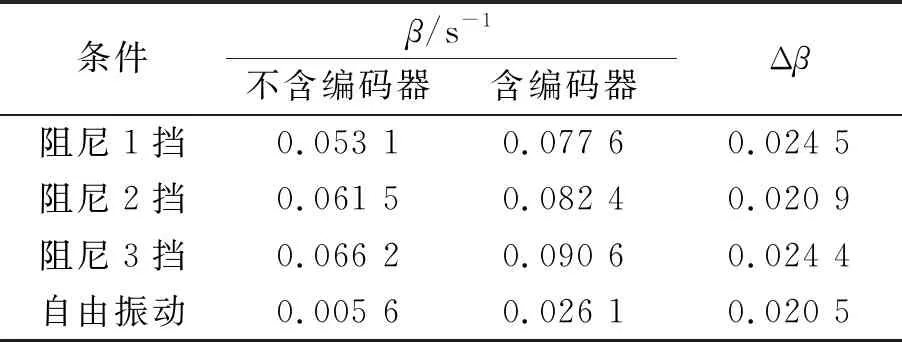
表1 编码器引入的阻尼

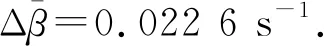
定量计算出的编码器阻尼系数虽然小于1挡电磁阻尼，相比于系统固有阻尼系数而言较大，因此不能忽略. 但添加编码器后对受迫振动及阻尼振动的观察不产生影响. 在研究阻尼振动和受迫振动时，应该使用由固有阻尼、电磁阻尼和编码器阻尼之和作为总的阻尼系数进行计算.

4 结束语

经过理论分析及实验验证可知，通过光电编码器和STM32单片机测量波耳共振仪的实时角位移时，分辨率和功能相比于原始仪器均显著提升，该方案可以将数据实时呈现在电脑上，有助于学生对机械振动有更直观的认识. 基于光电编码器的改进方案有能够获得大量实验数据的优势，可进行波耳共振仪基础实验验证以及混沌现象的探究. 借助于0.01 s的采样频率所获得的数据，可以方便地绘制角位移-时间曲线，由于数据采集的时间间隔很小，数据点拟合出的曲线精度很高；通过对等时间间隔采集到的角速度数据进行差分运算，可以得到某一时间所对应的摆轮角速度值，进而可以绘制出振动相图. 所以，使用光电编码器改进仪器后，使利用大量数据绘制图像来研究混沌现象成为可能，对振动的研究很有帮助.