基于RSSD 和小波变换的滚动轴承故障诊断

严文超，王伟奇，黄 蓉

1.湖北三峡职业技术学院，湖北 宜昌 443000；2.湖北中南鹏力海洋探测系统工程有限公司，湖北 宜昌 443000

滚动轴承是机械零部件中应用最广泛的一种，具有滚动摩擦阻力小、运转精度高的特点，其运行状况对设备性能影响明显，特别是高端机械装备中，如数控机床、风电装备、高铁机车、航空发动机、工业机器人等，滚动轴承的安装与旋转状态对装备的性能起着关键作用。轴承滚道的接触表面光滑、尺寸精密，反映轴承早期故障的状态特征微弱［1］。而且，滚动表面的损伤形状是无规则的，产生的振动将是由多种频率成分组成的随机振动［2］。实际工作时，电机转速和工况经常发生变化，传感器提取的振动信号具有非平稳性，还含有大量背景噪声，故障特征难以有效提取。因此，对故障特征提取技术的研究一直是滚动轴承故障诊断研究的关键。

2013 年，莫代一等［3］将基于信号共振稀疏分解（resonance-based sparse signal decomposition，RSSD）方法应用到滚动轴承早期故障诊断中，阐述了双重Q 因子的稀疏分解方法；陈向民等［4］将RSSD 方法应用于转子碰摩故障诊断中。He 等［5］在滚动轴承和齿轮故障诊断中利用RSSD 中的品质因子可调小波成功提取出相应的故障特征。CUI L L 等［6］针对RSSD 分别在转子碰磨故障和滚动轴承的局部单点故障的分析应用方面开展了大量研究，成功地从结果中提取了故障信息。这些研究都是对共振稀疏分解获得的低共振分量求取包络谱以提取故障特征，但实际应用发现在较强的背景噪声下，如此获取的故障特征频率成分并不明显，很多时候难以进行有效分析，因此可以尝试针对低共振分量采取进一步的时频分析。本文重点研究一种新的滚动轴承故障特征提取技术，即基于RSSD 与小波变换相结合的故障诊断方法。

1 信号共振稀疏分解方法

1.1 品质因子及共振属性的定义

共振稀疏分解法是根据振动信号中不同成分其波形特征（共振属性）不同来分解信号。共振属性的定义可以用品质因子Q 来阐述，Q 是信号中心频率f0与频率带宽B 的比值，属于无量纲参数，其表达式为：

品质因子的概念在小波分析中也有体现，传统的小波分析可看作品质因子恒定的情况。

品质因子可以表征信号的频率聚集程度，Q 越高则信号的频率越集中，共振属性也更高，表现在时域上的震荡次数也越多［7］。由品质因子量化信号共振属性，品质因子高的信号其脉冲的时域振荡次数多，表现为高共振属性；品质因子低的信号其脉冲的时域振荡次数少，表现为低共振属性。

1.2 可调品质因子小波变换

可调品质因子小波变换（tunable-Q factor wavelet transform，TQWT）依据信号的共振属性，采用带通滤波器组实现，其两通道分解、合成滤波器组如图1 所示。在图1 中参数β 为高通尺度因子（HPS），α 为低通尺度因子（LPS），r 表示冗余度。v0(n)为提取的低共振分量，v1(n)为提取的高共振分量，尺度因子在0 至1 间取值。

图1 两通道滤波器组：（a）分解滤波组，（b）合成滤波组Fig.1 Two-channel filter banks：（a）decomposition filter banks，（b）composite filter banks

多层分解过程就是将一个信号依次通过高频带通滤波器至低频通带通滤波器的过程，利用分解滤波器组进行连续迭代。图2 是3 层小波变换示意图。

图2 三层小波变换示意图Fig.2 Schematic diagram of three-layered wavelet transform

1.3 共振稀疏分解的实现过程

通过信号中不同成分的振荡特征将信号分解为不同组成分量，这是信号共振稀疏分解实现不同成分分离的基本思想。RSSD 方法首先利用TQWT 构建2 种Q 值不同的小波基函数库，然后对信号进行不同基函数库下的稀疏表示，最后使用形态分量分析法对信号采取非线性分离［8］，获得高共振分量（Q 值较大）和低共振分量（Q 值较小）。

给定一个观察信号x，它由2 个信号x1和x2线性叠加而成，x1主要包含具有持续振荡的高共振成分，x2主要包含具有瞬态冲击的低共振成分，采用形态分量分析（morphological component analysis，MCA）将信号中共振属性不同的分量分离开来，要求分离开来的2部分的耦合程度越小越好［9］。假定信号x1和x2可分别用基函数库S1和S2（二者相关性低，由TQWT 获得）来稀疏表示，可设定一个最小目标函数：

L1、L2为TQWT 分解的级数，S1为高品质因子TQWT 各级小波基组成小波基函数库；S2为低品质因子TQWT 各级小波基组成小波基函数库；W1和W2分别表示信号在小波基函数库S1和S2下的变换系数矩阵，即各级小波对应的变换系数组成的矩阵；高低共振分量的权重系数矩阵为λ1，λ2。

由品质因子Q 确定的小波基函数库S 决定了信号中不同的成分，直接关乎到分解的效果，权重系数矩阵决定了各部分的能量大小。在共振稀疏分解中参数的选择将直接影响到获取故障信息的效果，及不同成分的耦合程度。

品质因子Q 越大所体现的共振属性越高，其时域波形震荡次数越多，频率响应的分辨率越高，相邻两子带的重叠度越低［11］。在应用RSSD 进行信号分解时，不同成分通过不同共振属性的小波来拟合，因此Q 值的取值极大程度影响着高低共振分量的相关性（也就是耦合程度）。文献［12］给出了品质因子的相关性系数表达式：

式（7）中：Q1为高品质因子；Q2为低品质因子，一般取1。

2 小波分析基本理论

小波变换是一种信号的时间-尺度分析方法，具有多分辨率的特点，对低频信号可获得较高的“频率分辨率”和较低的“时间分辨率”，而对高频信号又可获得较高的“时间分辨率”和较低的“频率分辨率”，这个特性使小波分析对于不同信号具有极好的自适应能力，从而使小波分析广泛应用于信号分析领域［13］。

设x(t)在空间L2（R）是平方可积的，则该函数的小波变换可定义为以函数族ψa，b(t)为积分核的积分变换［10］：

函数族ψa，b(t)由基本小波函数ψ(t)通过平移和伸缩变换获得，即

ψa，b(t)又称为连续小波（简称小波），其中a 是尺度因子（又称伸缩因子），b 是定位参数（又称平移因子）。由式（9）可知，a 减小则小波的时宽减小而频宽增加，中心频率向高频处一段；反之，a增大则小波的时宽增大而频宽减小，中心频率向低频处移动。连续小波变换是一个线性变换过程，满足线性叠加特性，其实质是一个恒Q 的带通滤波器［14］。

图3 是小波分析多尺度分解的组织形式，以信号X 的三尺度分解为例，cA1、cA2、cA3对应的各层低频段，cD1、cD2、cD3对应的各层高频段；cA 为小波分解的近似信号，cD 为小波分解的细节信号。通过小波多尺度分解，可以有效观测信号的局部信息［15］。

图3 三层小波分解结构Fig.3 Decomposition structure of three-layered wavelet

3 在滚动轴承故障诊断中的实例应用

3.1 实验方案及数据说明

滚动轴承轴承故障数据选自美国西储大学电气工程实验室。实验时通过电火花加工的方式模拟轴承各类故障损伤，选用的轴承为深沟球轴承（型号为SKF 6205-2RS）。试验中采样频率为12 000 Hz，采样点数为8 192，电机转速约为1 800 r/min，即转频fr=30 Hz。根据轴承故障特征频率计算式，内圈故障特征频率fi=161 Hz，外圈故障特征频率fo=108 Hz。

3.2 滚动轴承内圈故障诊断

选取轴承内圈故障实验数据进行分析，其故障信号时域波形与频谱如图4 所示。从图4（b）中可以发现存在不明显的冲击，且噪声较强，在中高频段出现了大量的峰值群（峰值群中心频率约2 700 Hz，3 500 Hz），主要原因是内圈滚动损伤激发了元件固有振动［16］，但是由于信噪比低，低频段故障特征频率往往难以观察。

图4 内圈原始信号：（a）时域波形，（b）频谱Fig.4 Original signal of inner circle：（a）time-domain waveform，（b）spectrum

对内圈故障原始信号进行RSSD 分解，由一般经验选择低品质因子Q2=1，高品质因子Q1=4，冗余因子r1=r2=3.5，分解层数L1=29，L2=10，分解后的高共振分量见图5（a），低共振分量见图5（b）。观察可以看出，高共振分量中以谐波成分为主，低共振分量中存在明显的冲击成分。

为分析故障中冲击成分的特征，对低共振分量采用希尔伯特解调并求取包络谱。从包络谱图6 中可以看出存在故障特征频率161 Hz 及其倍频与转频的调制频率，如454 Hz，615 Hz（即3fi-fr，4fi-fr）。

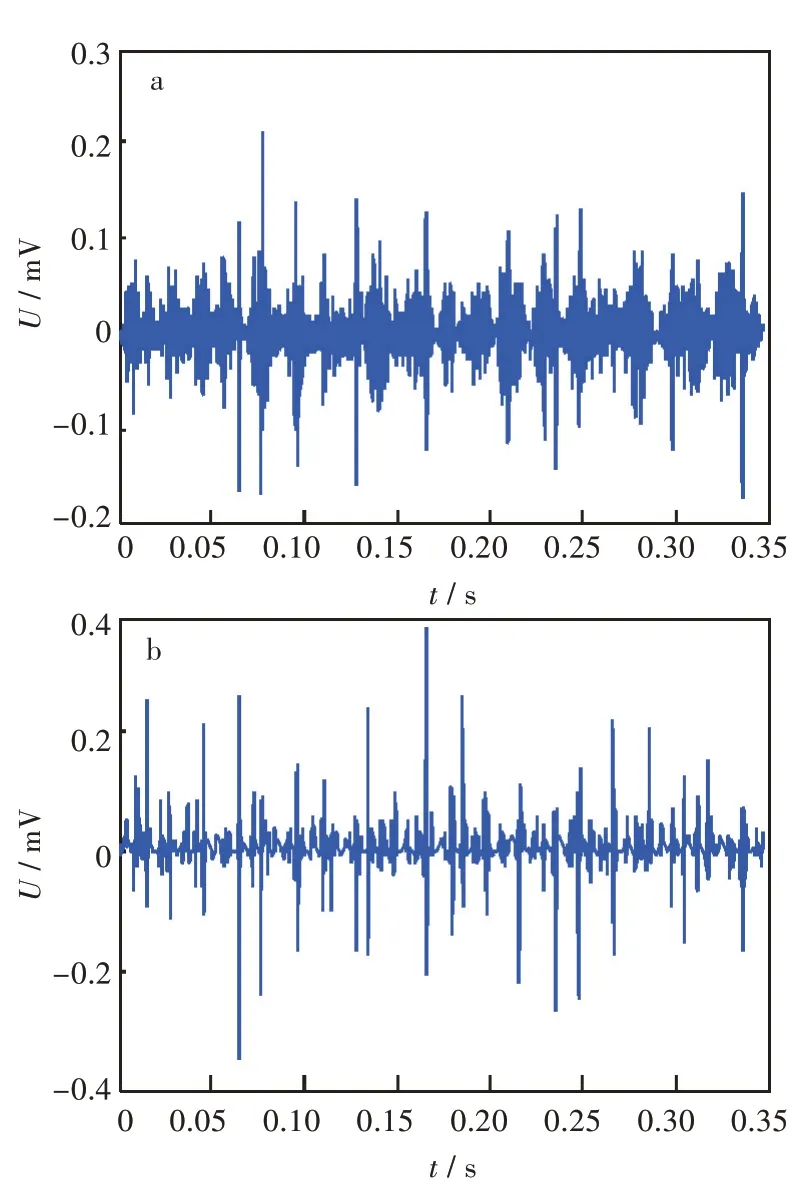
图5 内圈故障信号的共振稀疏分解：（a）高共振分量，（b）低共振分量Fig.5 Resonance sparse decomposition of inner circle fault signals：（a）high-resonance component，（b）low-resonance component

图6 内圈故障信号低共振分量包络谱Fig.6 Envelope spectrum of low-resonance component of inner circle fault signals

低共振分量所对应的包络谱中依旧存在大量的干扰，只能观察到较少的故障特征频率及其倍频。考虑到小波的多分辨率及局部优化特性，对低共振分量进一步进行小波分析［17］。选择db2 小波分解做5 尺度小波分解，并对第一层细节信号进行重构。其重构信号的时域波形及包络谱如图7所示。从图7（b）观察可以发现内圈故障特征频率（161 Hz）1 倍、2 倍、3 倍、4 倍等频率处峰值明显，与转频（30 Hz）相关的其他调制频率边频也较明显。由此可以判定出现了内圈故障。

3.3 滚动轴承外圈故障诊断

图7 低共振分量：（a）时域波形，（b）包络谱Fig.7 Low-resonance componentatime-domain waveformbenvelope spectrum

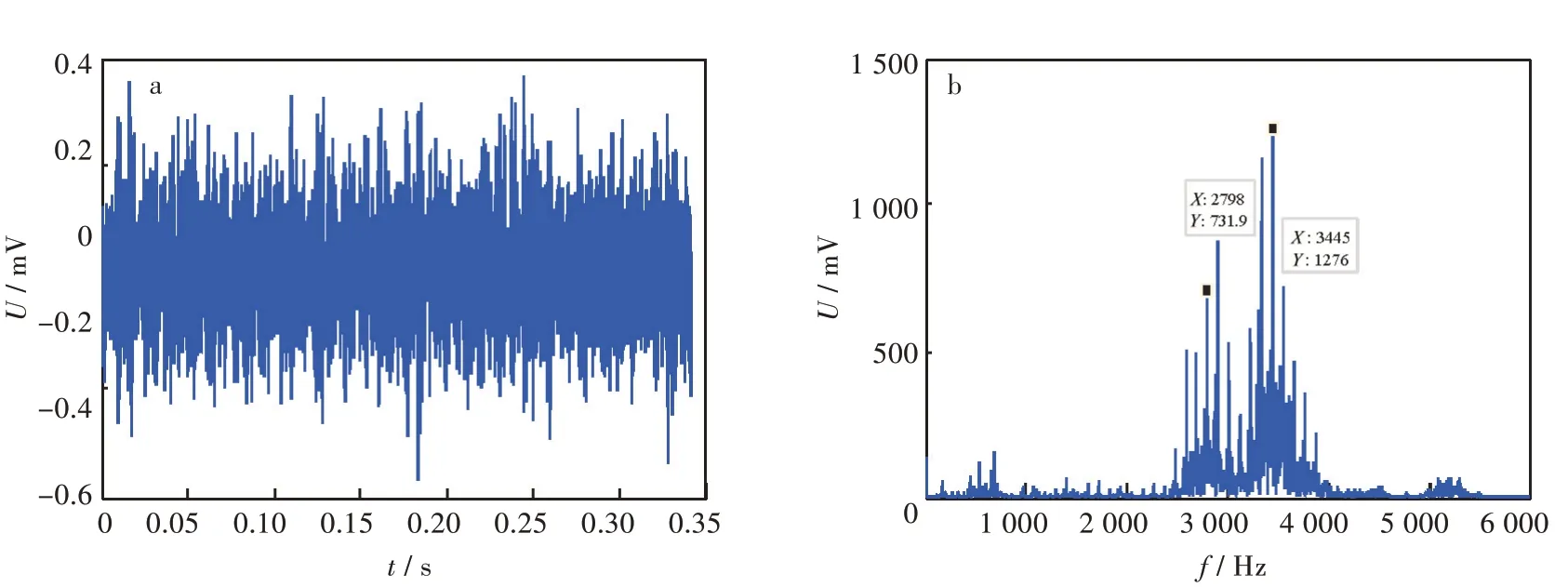
图8 外圈原始信号：（a）时域波形，（b）频谱Fig.8 Original signals of outer circle：（a）time-domain waveform，（b）spectrum

图9 外圈故障振动信号共振稀疏分解：（a）高共振分量，（b）低共振分量Fig.9 Resonance sparse decomposition of outer circle fault vibration signals：（a）high-resonance component，（b）low-resonance component

图8 为滚动轴承外圈轻度损伤时的振动信时域波形图和频谱，从图8 中可以发现存在故障冲击成分，但背景噪声较强，冲击间隔杂乱，无法明确冲击周期，在频谱中频率集中在固有频率3 500 Hz附近且幅值占优，信噪比低，故障特征频率处于低频段难以观察。

同样对外圈故障原始信号进行RSSD 分解，分解参数选择Q1=4，Q2=1，r1=r2=3.5，L1=31，L2=11，分解后的高共振分量见图9（a），低共振分量见图9（b）。以看出低共振分量存在明显冲击，这部分主要包含瞬态冲击成分，为故障信号所在分量。

为分析滚动轴承故障振动特征，对图9 所示低共振分量进行希尔伯特解调，其包络谱见图10。从图9 中可以看到在539.1 Hz 处峰值明显，即滚动轴承外圈故障频率108 Hz 的5 倍频处，但其他倍频处的峰值基本观察不到。

为更加凸显故障特征，对分解后的低共振分量进一步进行小波分析，与前面相同。第一层细节重构信号的时域波形及包络谱如图11 所示。从图11（b）观察可以发现外圈故障特征频率的1 倍、2 倍、3 倍、4 倍、5 倍等频率处峰值都比较明显，与转频（30 Hz）相关的频率成分干扰较小，由此可以判断为出现了外圈故障。

图10 低共振分量的包络谱Fig.10 Envelope spectrum of low-resonance components

图11 低共振分量：（a）时域波形，（b）包络谱Fig.11 Low-resonance component：（a）time-domain waveform，（b）envelope spectrum

4 结 语

在滚动轴承出现早期故障时，信号能量较微弱，由于背景噪声较大，故障产生的冲击振动信号表现不明显，因此经RSSD 方法获取的低共振分量有时故障特征也不占优，难以观察。针对于小波变换的局部优化及多分辨特性，考虑结合小波变换，对低共振分量进行进一步的细化分析，通过观察小波重构的信号及其包络谱能够更加凸显故障特征频率，便于分析判断。从实验实例中的应用来看，基于RSSD 和小波变换相结合的特征提取及故障分析方法在滚动轴承早期故障诊断中有较好的效果。