一种带变异算子的粒子群优化粒子滤波降噪算法

方 璐，范东亮，张光宇，陈汉新

武汉工程大学机电工程学院，湖北 武汉 430205

去噪是信号处理的重要内容，去噪的好坏对后续诊断结果的分析有着重要影响，研究非线性信号的去噪方法是近年来关注的重点［1］。黄名钿等［2］使用基于粒子群优化（particle swarm optimization，PSO）算法的参数小波阈值处理方法实现了对非线性信号的降噪处理。Ananth 等［3］使用基于粒子群优化的模糊滤波器，以除去信号中的高密度图像脉冲噪声。这些算法都能实现对非线性信号的去噪，然而使用PSO 算法结构，有易陷入局部最优解的缺陷，特别是处理多局部极值的信号，收敛速度和精度不高。为改善粒子群算法的缺陷，张荣光等［4］将粗糙集理论引入粒子群算法中，构建了离散粒子群优化方法，加强了搜索能力。Kar 等［5］提出了一种基于引力搜索算法（gravitational search algorithm，GSA）的粒子群优化算法（GSA-PSO），用于2 种常用模拟电路的优化设计，取得了不错的效果。

粒子滤波（particle filter，PF）算法在处理非线性问题上具有的独特优势，使得粒子滤波方法成为近年来国内外关注的重点［6］。已被广泛应用于故障诊断、导航定位、无线通讯、机器人定位、视觉跟踪等诸多领域［7］。然而常规粒子滤波采样过程中采用的采样策略和选择的次优重要性函数，使得其存在粒子贫乏和计算效率低等问题。用智能优化算法来优化PF 算法的采样结构，是现阶段PF研究的热点，其中基于PSO 算法的PF 算法是智能优化粒子滤波算法的代表之一。王尔申等［8］提出了一种基于边缘粒子滤波和粒子群优化的联合参数和状态估计的双估计方法，提高了PF 算法的性能。然而没有解决PSO 算法易陷入局部最优的问题，使得运算结果不稳定，去噪效果较差。为了改善PSO-PF 算法的性能，王尔申等［9］将混沌序列引入PSO-PF 算法中，还有学者将遗传重采样方法和PSO-PF 算法相结合［10-11］，这些措施都提高了PSO-PF 算法的滤波性能，然而随着算法的结构变得复杂，计算量也会加大，并不适合实时的去噪处理。

本文提出一种适用于滤波降噪的新型粒子群优化粒子滤波（novel particle swarm optimization particle filter，NPSO-PF）算法。该算法在采样过程中通过遗传变异控制函数，使粒子优化过程分为前后期，加快了粒子集的收敛，提高了运算速度。同时通过变异操作，控制粒子的多样性，避免了粒子贫乏，利用率不高的问题。将算法用于非线性信号的降噪具有稳定，快速，有效的优点。本文首先介绍PF、PSO 和PSO-PF 算法原理并分析其缺陷，然后构造出NPSO-PF 算法。为验证变异算子的性能，先进行迭代仿真实验，为验证NPSO-PF 算法的滤波性能，进行了状态估计实验，为验证NPSO-PF 算法的滤波降噪，进行了去噪仿真实验。

1 常规粒子滤波算法及其不足

1.1 粒子滤波原理

PF 算法的本质是基于蒙特卡洛法的最优贝叶斯估计。主要根据系统状态向量的经验条件分布产生的粒子样本来模拟给定系统的当前状态，然后根据各个时刻的测量值不断修正和调整粒子的权值及位置，最后通过调整后的粒子信息修正最初的经验条件分布以获得最精确的估计值［12］。

选取非线性动态系统状态方程和观测方程模型如下：

其中xk为k时刻的系统状态，yk为观测输出，别为非线性函数。

PF 的具体实现步骤如下：

步骤1：初始化。在k=0 时刻，根据P(x0)分布采样得到{即。

归一化重要性权值

步骤3：重采样。根据重要性权值ω~i

k从集合中重新采样得到k 时刻的新粒子集合，根据得到新的粒子权值。

步骤4：输出。状态估计为：

1.2 常规粒子滤波的不足

常规PF 算法的核心算法的主要缺陷是会出现样本贫化的问题。位于先验概率分布尾部的观测概率或似然函数，使权值更新后的粒子权值会很小。差异很小的粒子表示的后验概率，重采样后，粒子样本集的多样性会很小甚至只剩单一样本［13］，从而产生粒子贫乏的问题。

当系统初始状态未知时，需要采集大量粒子样本才能实现系统的状态估计是常规粒子滤波的另一个缺陷。采集的粒子数目很小，粒子很难收敛到真实状态附近，实现准确的估计；增大粒子集的数目，计算量增大，计算效率低下，不适合实时监测的问题。

2 粒子群优化粒子滤波算法及其不足

2.1 粒子群优化算法原理

PSO 算 法 是Kennedy 和Eberhart 等 于1995 年最先提出的，它通过群体中粒子个体间的协作和竞争来有效的实现复杂空间全局最优解的搜索，是一类模拟群体智能行为的优化算法［14］。具体可表述为：随机初始化一个N 维空间数量为m 的粒子 群 。 其 中 第 i 个 粒 子 位 置 为，其速度它的个体极值为，种群的全局极值为。确定上述两个极值后，就可以根据下述公式来不断更新粒子的速度和位置：式（5）中：r 是介于( 0，1) 区间的随机数，c1和c2统称为学习因子或加速度因子，一般c1=c2=1.469 2。ω 为惯性系数。

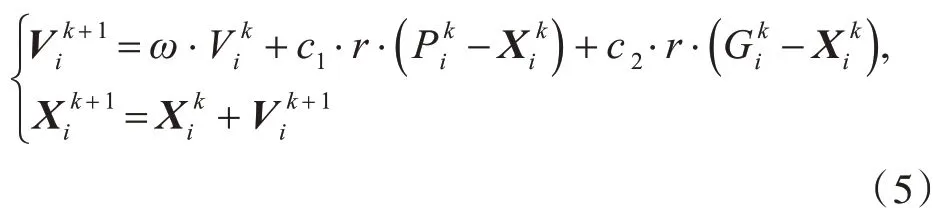
2.2 PSO-PF 算法

将PSO 算法融合到PF 算法中，将最新的观测值引入到粒子样本的采样过程中，并定义粒子群优化算法中的适应度函数为：

其中，Rt是观测噪声方差，Ynew是最新的观测值，Ypred是预测观测值。

在采样过程中，如果粒子集分布在真实状态附近，根据式（6）可知，粒子的适应度值会很大。而不在真实状态附近的粒子其适应度值就会很小。此时利用PSO 寻优算法，根据当前最优值和公式（5）不断地更新每个粒子的速度与位置，使得粒子不断地向真实状态附近移动。从而避免遗漏重要粒子，既保证了粒子的多样性，又提高了有效粒子的使用率。

2.3 PSO-PF 算法的不足

PSO-PF 算法的实质是在PF 算法的采样过程中先利用PSO 算法将粒子集向真实状态附近集中，在重采样过程中能有效的采集对估计真正起作用的粒子，从而提高PF 的效率和精度。然而传统的PSO 算法在迭代后期，粒子的速度越来越小使粒子在局部空间范围内反复搜索，容易出现局部最优现象。而随着所有粒子都随公式（5）不断向局部最优值移动，使粒子丧失了多样性，从而降低了PF 的精度和效率。

3 带变异算子的PSO 优化PF 算法

3.1 带变异算子的PSO 算法

为了改善常规PSO 优化算法易陷入局部最优解的问题，鉴于遗传变异算法的变异思想，将遗传算法的操作算子引入到PSO 算法中［15］。其具体做法是引入一个变异控制函数，用来控制变异的粒子数目，以保持种群内部的多样性，进而避免过早的在局部最优处收敛。

引入的变异控制函数为：

其中h 表示当前迭代次数，hmax表示最大迭代次数，α、β 表示控制系数。

根据式（7），计算变异算子的控制率：

其中u 是变异率，m 是预设变异率，设定后不变。

根据式（8），计算变异操作的粒子数目：

根据式（9），随机从粒子群中选取要进行变异操作的粒子，用实数编码。假设第k 个粒子被选中进行变异操作，如其中第j 个元素进行变异，则操作策略为：

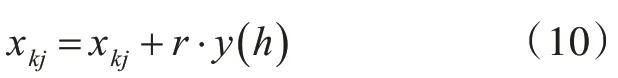
其中r ∈( )-a，a 是随机数。

动态惯性系数的计算为：

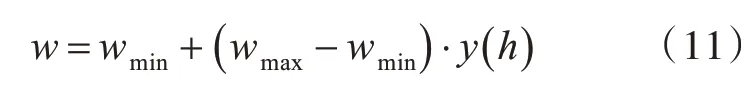
其中，wmax表示最大惯性系数，wmin表示最小惯性系数。

变异算子控制PSO 算法的运行是通过粒子的变异率，动态惯性系数和变异操作来实现的。而变异率是由式（7）确定，动态惯性系数是由式（11）确定，变异操作是由式（8）～式（10）来完成的，其都与算法的迭代次数相关的。在算法迭代的前期，控制函数和动态惯性系数取较大的值，进行变异操作的粒子数目和变异尺度都比较大，既保证了种群内部粒子的多样性，又使得PSO 算法大范围的在解空间内进行搜索。在算法的后期，控制函数和动态惯性系数取较小的值，进行变异操作的粒子数目和变异尺度都很小，甚至不进行变异操作，既使种群内部的粒子能很快进行收敛，又使PSO 算法小范围的在解空间内进行搜索。因此，算法的收敛速度和收敛精度都得到了提高。NPSO 算法具体步骤为：

步骤1：初始化群体数目N，学习因子C1和C2，惯性系数w，初始粒子的位置Xi和速度Vi，最大迭代次数hmax，预设变异率m。

步骤2：按式（7）计算控制函数y()h ，按式（11）计算惯性系数w。

步骤3：根据式（8）计算变异率u，根据式（9）计算变异粒子数M，按式（10）进行变异操作。

步骤4：对于每个粒子，按式（6）适应度值fit[i] ，并与其个体最优值Pi进行比较如果fit[i ]＞Pi那么令。

步骤5：求解全局最优值Gi，即如果Pi＞Gi那么令Gi=Pi。

步骤6：根据式（5）更新粒子的速度Vi和位置Xi；

步骤7：当达到最大迭代次数或者粒子群的最优值符合某阀值ε 时，则输出结果，否则返回第二步。

3.2 NPSO-PF 算法

NPSO-PF 算法的原理是利用带变异算子的PSO 算法快速准确的收敛性能来优化PF 的采样过程。通过适应度值使所有粒子向最优粒子移动，以改善粒子集的分布情况，使粒子集都集中在真实状态附近，从而提高了滤波的精度和效率，具体的步骤为：

步骤1：初始化。在k=0时刻，根据P(x0)分布采样得到即。步骤2：NPSO-PF 优化粒子集分布。结合利用3.1 节讲述的NPSO-PF 实施步骤对粒子群进行寻优，当达到迭代次数或者粒子群的最优值符合某阀值ε时，输出粒子，即可得到新的粒子样本x^ik。

步骤5：输出。根据式（4）得到更新后的状态估计。

4 试验仿真与结果分析

4.1 标准PSO 和引入变异算子的PSO 仿真对比

为了验证加入变异算子的粒子群优化算法具有不陷入局部最优值的性能以及其准确性和收敛精度，给定非线性函数为：

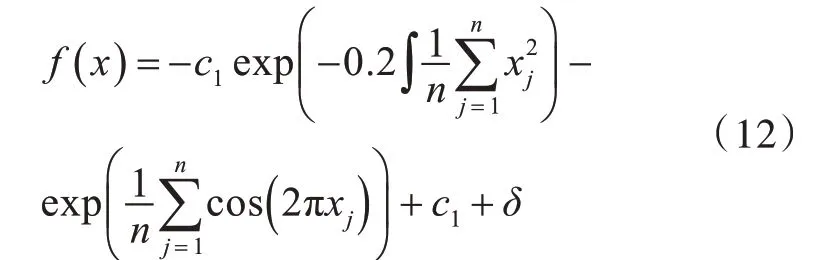
取c1=20，n=2，δ=2.71282 时，该函数为有很多局部极小值的Ackley 函数。用此时的f()

x 为目标函数，可以有效的测试算法的收敛性能。分别用引入变异算子的PSO 算法和标准PSO 算法对函数进行寻优。根据相关参考文献和经验以及多次试验，其中仿真参数分别为：粒子个数N=30，适应度阈值ε=0.001，最大迭代数hmax=100，变异控制系数α，β 分别为1.7 和10，惯性权重ω 最大和最小值分别为0.729 8 和0.1，加速度常数c1和c2分别为1.469 2。计算机的处理器是Inter（R）Core（TM）i7-4970 CPU@3.60 GHz 3.60 GHz。随机取某次仿真结果如图1 所示。

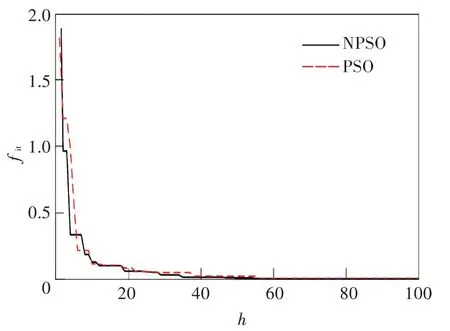
图1 两种算法的迭代曲线Fig.1 Iteration curves of two algorithms

从图1 可以看出，带变异算子的PSO 算法在早期和后期的收敛速度快于标准PSO 算法，中期略低于标准PSO 算法。为了比较2 种算法的整体收敛性能，在上述实验函数和参数不变的情况下，分别进行了20 次实验，得到了2 种算法的迭代次数和收敛函数值的平均值。MATLAB 运算结果表明，标准PSO 算法的平均收敛迭代次数为60 次，引入变异算子的PSO 算法为40 次。收敛时的适应度函数平均值分别为0.010 和0.001。结果表明，带变异算子的PSO 算法在函数优化中的应用优于标准的PSO 算法。

4.2 粒子滤波仿真试验及对比

为验证3 种算法的滤波和估计性能，试验选取的动态非线系统的状态方程和观测方程。

状态方程：

观测方程：

其中vk-1和nk为零均值高斯噪声。xk为状态变量，yk为观测变量。k 为模拟步长。利用PF算法、PSO-PF 算法、NPSO-PF 算法分别对该非线性系统进行状态估计和跟踪，为比较3 种算法的性能，粒子数分别取n=50，500，1 000，取初始状态概率密度函数为N(0，2)，测量噪声方差和过程噪声方差分别为Rt=1×10-3和Q=1×10-2，模拟步长为k=50，粒子群优化算法相关参数同上，估计值和真实值之间差值的绝对值用σ 表示。随机选取不同粒子数目下某次仿真结果如图2 所示。其中均方根误差R 的计算公式为：

为了比较3 种算法的整体性能，将仿真实验进行30 次，测得在3 种不同粒子数目下3 种算法的30 次运算的均方根误差和程序运行时间的平均值，如表1 和表2 所示。

从图2 可知，NPSO-PF 算法估计出的粒子状态更接近粒子的真实状态，估计误差也更小，随着估计的粒子数目的增加效果越来越明显。而PSO-PF算法的估计性能略好于PSO 算法，并随着粒子数目的增加效果差异越来越小。从表1 和表2 的结果来看，NSPO-PF 算法的平均估计误差和运行时间要低于另外两者，随着粒子数目的增加，效果更明显。而PSO-PF 算法只是略好于PF 算法，随着粒子数目的增加两者性能基本相同。综上可知，NPSO-PF 算法比PSO-PF 和PF 算法具有更好的、更稳定的估计性能。

图2（a）n=100，（c）n=500，（e）n=1 000 状态估计曲线；（b）n=100，（d）n=500，（f）n=1 000 误差曲线Fig.2（a）n=100，（c）n=500，（e）n=1 000 state estimation curves；（b）n=100，（d）n=500，（f）n=1 000 error curves

表1 三种算法的RTab.1 R of three algorithms

表2 三种算法的运行时间Tab.2 Running times of three algorithms

表3 三种算法的仿真降噪结果对比Tab.3 Comparisons of simulated noise reduction results from three algorithms

4.3 降噪实验仿真

利用上述3 种方法对下列信号进行降噪仿真实验，选取的原始信号方程如下：

加入大小和原始信号一样的随机噪音信号后得：

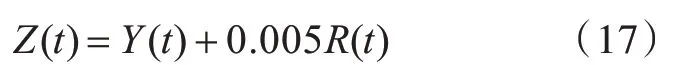
用原始信号方程（16），加噪信号方程（17）分别代替4.2 节中状态方程（13）和观测方程（14），从而构成3 种算法中的空间模型，其中Y(t)为原始信号峰值变量，Z(t)为加噪信号峰值变量，t 为模拟时间步长。其中取初始概率密度函数为N(0，2)，状态初始值为1，测量噪声方差Rt=1×10-4，过程噪声方差Q=1×10-5，模拟时间步长为t=204 8，PSO 算法相关参数同上，分别对4.2 节中3 种粒子数目进行实验仿真，现将粒子数n=100 时分别用PF 算法，PSO-PF 算法和NPSO-PF 降噪后的结果展示如图3 所示。

图3 降噪仿真实验结果：（a）原始信号，（b）原始信号加噪，（c）PF 算法降噪，（d）PSO-PF 算法降噪，（e）NPSO-PF 算法降噪Fig.3 Simulation experiment results of noise reduction：（a）original signal，（b）original signal plus noise，（c）noise reduction by PF algorithm，（d）noise reduction by PSO-PF algorithm，（e）noise reduction by NPSO-PF algorithm

从图3 可以看出，3 种算法都具有相当不错的降噪效果，用NPSO-PF 算法降噪后的信号峰值更清晰。信噪比是指原始信号与纯噪音信号的比值，信噪比数值越大表示噪音越小，因此信噪比是衡量降噪效果好坏的重要指标。为了更好比较3种算法的降噪性能，对上述实验结果进行信噪比S分析。取50 次降噪实验3 种算法在3 种粒子数目下的信噪比均值进行分析，其结果如表3 所示，信噪比计算公式为：

从表3 可以看出经NPSO-PF 算法滤波后的信噪比在3 种粒子数目的试验下都要比其他2 种算法高，而经PSO-PF 和PF 算法滤波后的信噪比基本一样。说明NPSO-PF 算法的降噪性能要优于其他2 种算法，而PSO-PF 和PF 算法的降噪性能基本一样。NPSO-PF 算法的信噪比提高值普遍大于其他两种算法，并且随着粒子数目的增加有持续上升的趋势，而PSO-PF 和PSO 算法基本达到饱和。综上所述，NPSO-PF 算法具有更好更稳定的滤波降噪性能。

5 结 语

本文将变异算子带入PSO 算法中，构成新型NPSO 算法，改善了PSO 算法的结构，优化了传统PSO 算法易于陷入局部最优解的问题，提高了PSO算法的性能。将其与粒子滤波算法相结合构成NPSO-PF 算法，该算法不仅具有更好的估计性能，而且在滤波降噪方面也有更好的效果。仿真实验结果证明NPSO-PF算法适用于信号的滤波降噪处理。