基于MIDAS GTS分析地铁运行振动对地铁车站沉降影响★
古丽革乃·依力哈木 周美均 郑欣欣 梅 钢
(中国地质大学(北京)工程技术学院,北京 100083)
1 概述
地铁的大规模修建,给人们的生活和出行方式带来了许多便利的同时,地铁的振动将不可避免的对地铁站本身和所在地层及沿线的建筑物产生了影响。在国际上,振动已被列为七大公害之一。地铁运行时产生的振动会使沿线建筑物,地层发生受迫振动,可能会引起地层的不均匀沉降,甚至开裂等问题[1]。如上海地铁一号线建成后未通车期间沉降基本没有发展,但通车后8个月沉降增加了3 cm~6 cm,4年内部分沉降甚至达到14 cm,这跟地铁动荷载作用下土体结构的改变和破坏,发生残余变形有关。
MIDAS/GTS是针对岩土工程而开发的有限元软件,该软件具有前后处理功能强大的岩土材料模型库,能满足大部分岩土体的破坏模式[5],因此用该软件对地铁车站及其所在地层进行数值模拟,比较接近真实情况,且计算结果相对安全。
本文运用MIDAS/GTS软件建立了空间有限元模型,模拟地铁振动,通过对地铁运行时的振动对沿线地层的影响和地层的沉降进行了空间模型的模拟研究,并对地铁运行和地下空间合理利用提供了一定的理论支撑。
2 建立模型和分析计算
2.1 模型的几何尺寸
本次研究根据中华人民共和国国家标准GB 50157-2013地铁设计规范及实地调查和查阅相关资料建立了一个一层三跨的地铁车站模型,该车站底板埋置深度为17.2 m,车站高度7.2 m,围护层厚度为0.5 m,方柱边长为0.7 m。地铁车站横断面详细尺寸如图1所示。
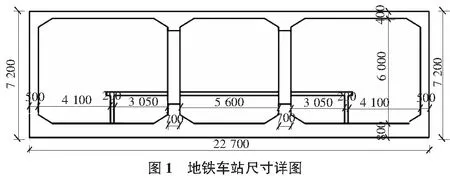
2.2 地铁车站和土层的物理参数选取
地基部分,计算宽度为22.7 m,高度为20 m,地铁车站埋深为17.2 m。根据北京地区的工程地质条件,地铁车站建立在粉质黏土层,其上为填土层,其下为黏土层和风化岩层,三层厚度均为10 m。相应的土层物理参数见表1。
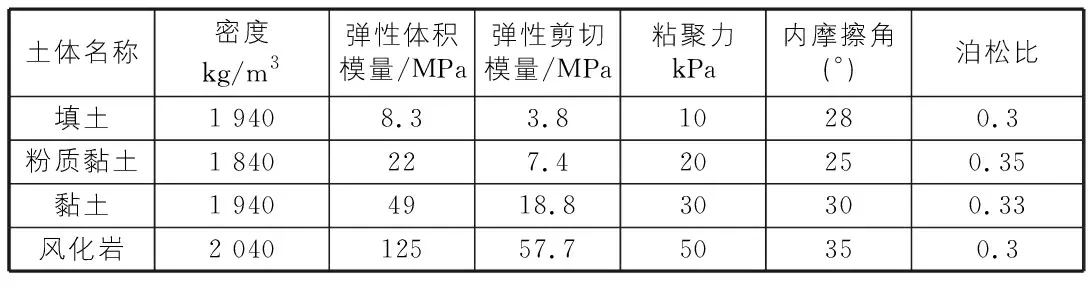
表1 土层摩尔—库仑模型参数取值
2.3 运用MIDAS GTS建模
运用MIDAS GTS软件基于收集的参数,建立三维地质模型,屈服函数为Mohr-Coulomb屈服准则(M-C准则)。模型采用二维单元中的高阶单元划分网格, 采用六面体单元作为结构的主单元, 利用四面体单元或三棱柱单元作为调解用不同尺度划分结构时的过渡型单元[3]。模型共3 881个单元,2 057个节点。考虑到地铁车站实际受力情况及边界效应,将模型作适当简化,模型尺寸为62.7 m×37.2 m×120 m。模型如图2所示。
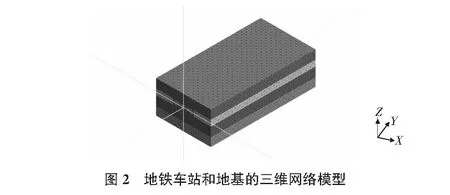
支撑边界包括模型的左右边界和下边界;桩的计算采用梁单元;钢筋混凝土预制管桩的承台也采用梁单元模拟,每根桩的桩顶集中载荷近似取其分担的建筑面积对应的载荷进行计算, 单位建筑面积载荷取准永久载荷标准值,为20 kN/m[4]。
3 计算分析
此次研究采用解决半无限域空间问题最常用的有限元数值方法在截取的有限域上设置人工边界。
3.1 边界条件选取
分析结构—地基动力相互模型,设置合理的人工边界对正确反映结构—地基整体动力特性很重要。在人工边界中,目前广泛应用的有粘性边界、粘弹性人工边界、透射边界等动力人工边界,这些边界主要是基于单侧波动概念的时域局部人工边界来的,粘弹性边界可以约束动力问题中的零频分量,能够模拟人工边界外半无限介质的弹性恢复性能,具有良好的稳定性和较高的精度。本次模型分析使用的是粘弹性边界。
3.2 荷载施加
模型建立以后,在模型上施加自重荷载,在施加自重荷载之前,先定义静力荷载工况,在静力荷载工况中定义模型的自重荷载。分析静力荷载工况得出了模型在自重条件下的各个方向上的位移、应力等的分布云图,以及模型各个节点的具体位移量。自重荷载下模型的变形分析结束后,进行地铁列车振动下的地基变形分析。对模型施加列车动态荷载条件,使用时间—力函数,通过动力模型模拟8节车厢的列车(80 km/h)运行8 s的情况下对周边地层的影响。
此次动力分析采用的是线性时程分析法中的直接积分法。时程分析法即结构直接动力法,是最经典的方法之一,直接积分方法的优点是可以考虑刚度和阻尼的非线性特点,计算相对准确。此次分析采用波动法进行地铁振动的输入,振动波的传播顺序是轨道→车轮振动→隧道结构→周围土壤。
4 计算结果分析
4.1 计算结果
利用MIDAS GTS分别计算仅自重条件下和列车运行振动条件下地铁车站的沉降过程。分析比较了列车运行振动对地铁车站的沉降影响。
仅在自重条件地铁站周围地层最大的沉降量位于地铁车站底部,在各个水平面上从地铁站中部越靠近边界随水平距离的增加沉降量逐渐减小。由于地铁站在自重条件下向下沉降,使得边界土层被挤压,有向上的位移,但位移量很小。总体来说,随着埋深的增加,沉降量呈先增大后减小的趋势。仅自重条件下地铁车站沉降云图如图3,图4所示。

4.2 计算结果的分析
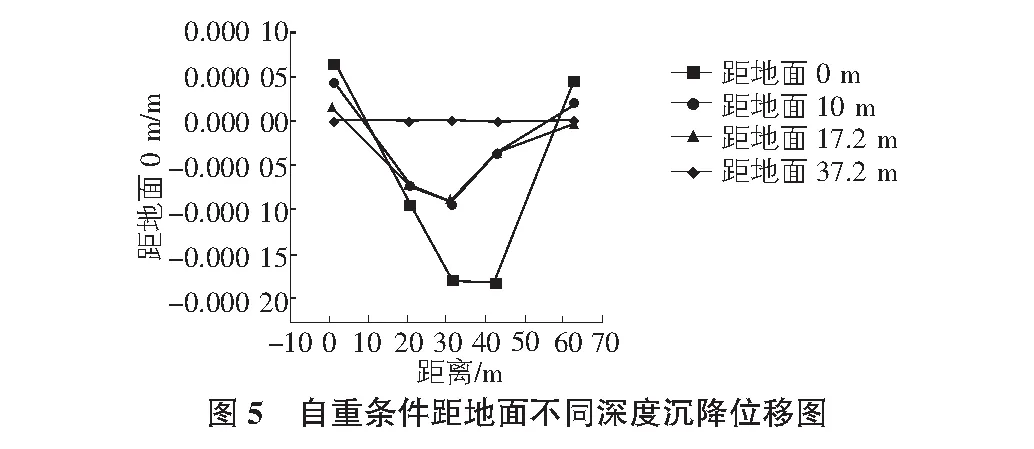
计算时分别在土层和地铁站的四个角点,顶部和底部的中点设置了监测点,记录了不同埋深下土层和地铁站的沉降量,并根据具体数值比较仅有自重引起的沉降和由地铁列车振动引起的沉降,见图5,图6。
从自重条件下距地面不同深度沉降位移图可以看出:
1)距离地面0 m处,沉降量在边界—模型中部—边界呈先增大然后减小的趋势;
2)由于模型中部沉降量最大,使得边界土层被挤压,从而有向上的位移,但位移量很小;
3)比较距地面不同深度处的沉降量,随着深度增加,沉降量减小。

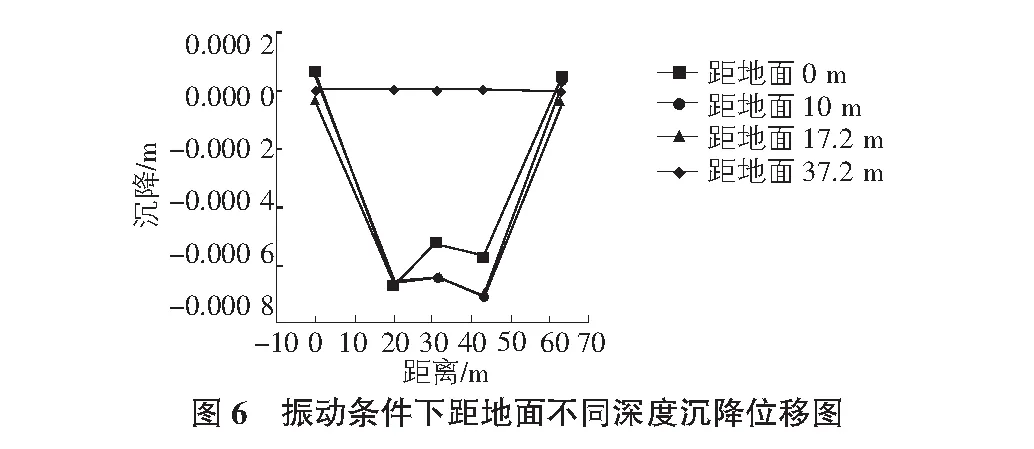
从列车振动条件下距地面不同深度沉降位移图可以看出:
1)列车振动情况下在各个水平面上从地铁轨道处开始随水平距离的增加沉降量逐渐减小,在远处沉降量逐渐趋于零;
2)在竖直截面上地层沉降量从地铁底部随深度的增加逐渐减小直至为零。
5 结语
本文基于MIDAS GTS 建立地铁站及所处地层的三维地质模型,并对模型进行数值模拟,得出以下结论:
1)从模型Z轴方向的位移云图中可以看出,列车振动情况下周围地层沉降量最大处为两个列车轨道下方的车站底部处。两个相向轨道中间处车站底部的地层在两向动荷载叠加的效应下沉降量也很大。同时由于地铁车站为钢筋混凝土结构,刚性较大且地铁车底部下方地层沉降不均匀,使得地铁车站顶部地层沉降量略小于地铁车站底部。而在地表面处,沉降量最大处对应在两相向轨道对称轴线上方。
2)列车振动情况下周围地层最大的沉降量位于地铁车站底部(列车运行轨道处),在各个水平面上从地铁轨道处开始随水平距离的增加沉降量逐渐减小,在远处沉降量逐渐趋于零;在竖直截面上地层沉降量从地铁底部随深度的增加逐渐减小直至为零。
3)由此模型计算出的地铁振动产生的地层位移云图可以看出,地基变形主要发生在Z轴方向,列车运行8 s后Z轴方向的最大沉降量为-9.26 E-04 m。依此推算,在未对地层进行特殊处理的情况下,以列车间隔时间10 min为例,其运行一年可使周边地层的最大沉降量达到数十厘米。此结果表明地铁列车运行对周围地层的不均匀沉降有很大影响,因此列车振动对周边地层的影响是不可忽略的,应对地层采取相应措施或控制列车运行振动参数减轻其影响。
以上结论在肯定了地铁列车运行对周围地层产生不均匀沉降影响很大的同时,也得到了地铁运营使地层产生不均匀沉降影响的基本规律。在工程实践中可据此着重处理沉降量较大的区域,预防或减轻地铁列车运营对地铁车站或地铁隧道的影响。

