深基坑桩锚支护数值模拟对比研究

陈俊成 曾 洲 杨 惺

(华南理工大学土木与交通学院土木工程系，广东 广州 510510)

1 概述

城市为了满足人口、交通和经济等各方面的需求不断地开发地下空间，而深基坑顺应这种趋势应运而生。深基坑的施工存在很多风险，为了防患于未然，有必要对深基坑的支护结构的变形和受力进行研究。王超、丁海涛[1]采用MIDAS对桩锚支护结构进行数值模拟，得到了各个工序下基坑的隆起情况和支护桩的内力，并对基坑进行了优化。周勇、李康[2]采用ADINA对桩锚支护结构进行基坑开挖数值模拟，得到了不同因素对支护结构位移的影响。

本文以广东省惠州市惠城区水口镇尚东公馆基坑西侧桩锚支护结构为研究对象，运用理正深基坑7.0PB4和MIDAS-GTS分别计算基坑西侧不同施工阶段支护结构的位移和弯矩，对比分析得出了支护桩的变形和内力变化特点。

2 工程概况

2.1 工程简介

尚东公馆基坑工程位于惠州市惠城区水口镇，地下室为地下2层，基坑周长约252.55 m，基坑深度8.00 m～8.68 m，基坑安全等级为二级，基坑使用年限为1年。

2.2 基坑支护方案

基坑西侧采用上部1∶1.5放坡，下部采用φ800@1 200灌注桩+2道锚索支护；基坑的外侧采用φ800@600搅拌桩止水。

2.3 土层基本力学参数

表1 基坑西侧土层的基本力学参数

基坑西侧设计用到的土层基本学参数如表1所示。

2.4 施工工况

基坑西侧的施工工况如表2所示。

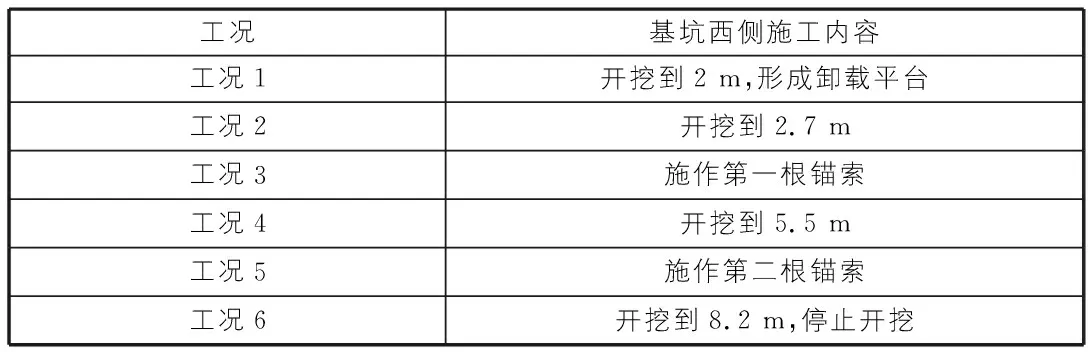
表2 基坑西侧的施工工况

3 解析法

对尚东公馆基坑西侧桩锚支护结构采用理正深基7.0PB4软件进行解析计算模拟。

3.1 静力计算模型

理正深基坑计算系统在结构静力计算中将地下排桩简化为弹性地基竖直梁[3]，并采用m法计算。

3.2 计算参数及模型

地面超载取20 kPa；不考虑地下水的影响；按JGJ 120—2012建筑基坑支护技术规程[4]和JGJ 94—2008建筑桩基技术规范[5]相关规范取m值，见表3。

表3 基坑西侧土层的基本力学参数

尚东公馆基坑西侧桩锚支护结构的解析法计算模型如图1所示。

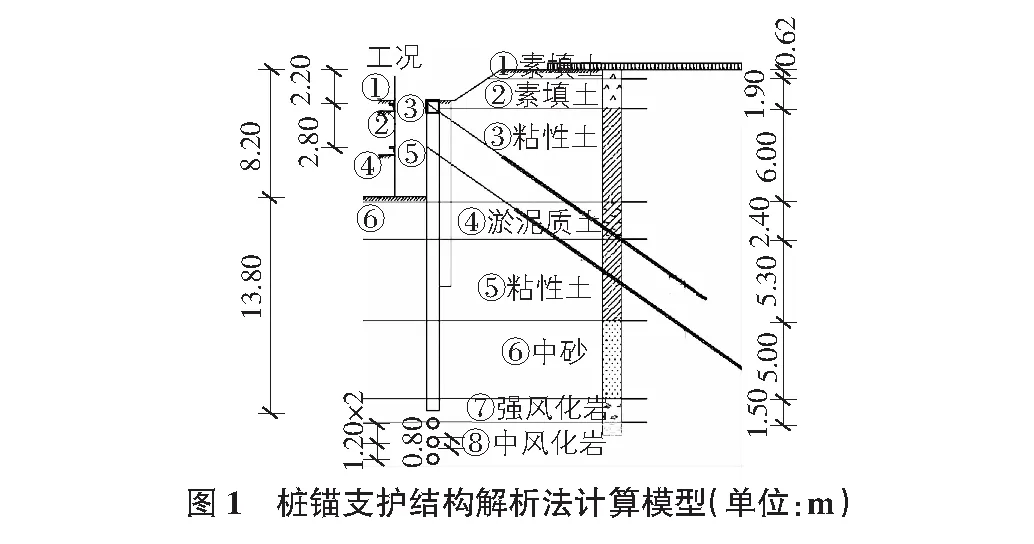
4 数值分析方法

对尚东公馆基坑西侧桩锚支护结构采用MIDAS-GTS进行数值模拟计算。

4.1 模型单元及计算参数的选定

1)土体：平面应变单元；灌注桩：直线梁单元+桩土接触单元；锚索自由端：桁架单元；锚索固定端：植入式桁架单元。

2)计算模型：土体—摩尔库仑模型；灌注桩和锚索—弹性模型。

3)计算参数：灌注桩采用直径为800 mm的圆形截面；第一根锚索采用3×7φ5的钢绞线，第二根锚索采用4×7φ5的钢绞线；锚固体直径均为150 mm。

4)边界约束条件：左右：水平约束；底部：竖向约束+转动约束；其他位移边界自由。

5)地面超载取20 kPa。

4.2 模型网格的划分

以0.5 m的间距划分模型网格，基坑西侧桩锚支护结构的数值模拟图形如图2所示。

5 结果分析

5.1 桩身位移对比分析

理正深基坑7.0PB4采用的是解析法，而MIDAS-GTS采用的是有限元数值模拟法，两种不同的方法计算出不同工况下灌注桩桩身位移分别如图3a),图3b)所示。

两种方法得到的支护桩在不同工况下的桩身最大位移、位置以及位移特点如表4所示。

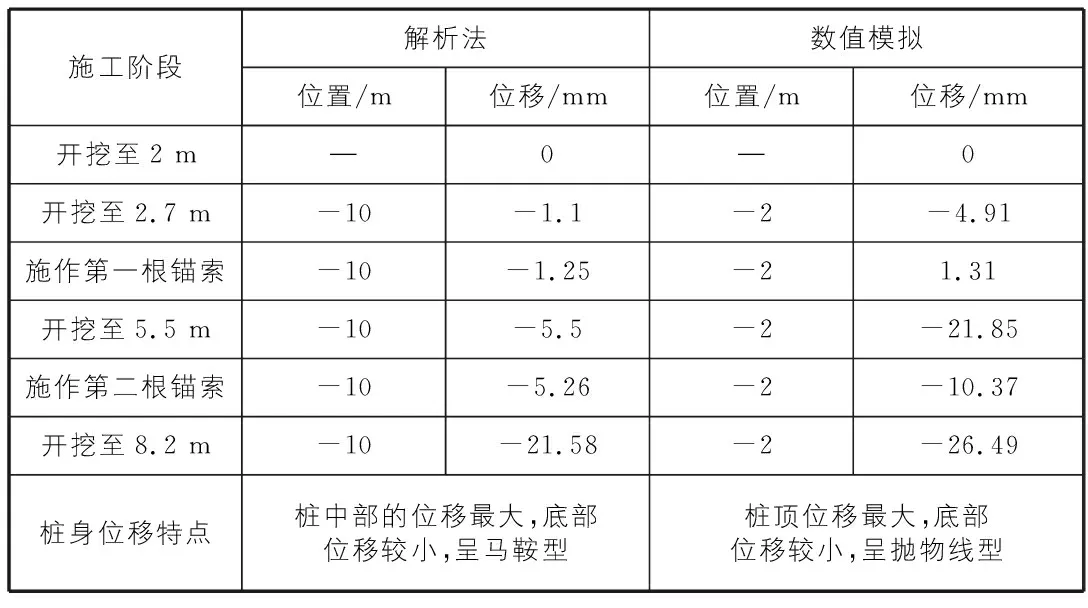
表4 两种方法计算灌注桩桩身最大位移位置，大小及特点

分析解析法得到的灌注桩桩身位移随施工阶段的变化可以发现，桩身位移呈现桩中部位移最大，桩底位移较小的特点。原因为：随着基坑逐渐开挖，由于有冠梁将灌注桩连在一起和受到了锚索的约束，故桩顶的位移会较桩中部的位移小，而桩的中部没有约束，故桩的最大位移出现在桩的中部；桩底由于是锚固端，故几乎没有位移。 分析数值模拟法得到的灌注桩桩身位移随施工阶段的变化可以发现，桩身位移呈现桩顶位移最大，桩底位移较小的特点。原因为：数值模拟法考虑了开挖2 m边坡对桩身侧向位移的影响，故数值模拟法的桩身位移会相较于解析法得到的桩身位移偏大；此外由于模型采用的是2D模型，并未考虑冠梁的存在及作用，故桩顶在未施作锚索时是无约束条件的，故支护桩的位移会呈现上大下小的特点。施作锚索后只能减小桩中上部的位移，但是上大下小的特点依旧没变。

对比分析解析法和数值模拟法得到的灌注桩桩身侧向位移，我们可以发现深度10 m以上的桩身侧向位移有较大的差异，深度10 m以下的桩身侧向位移只有较小的差异。

5.2 桩身弯矩对比分析

两种不同的方法计算出不同工况下灌注桩弯矩分别如图4，图5所示。两种方法得到的支护桩在不同工况下的桩身最大正负弯矩大小和位置如表5所示。

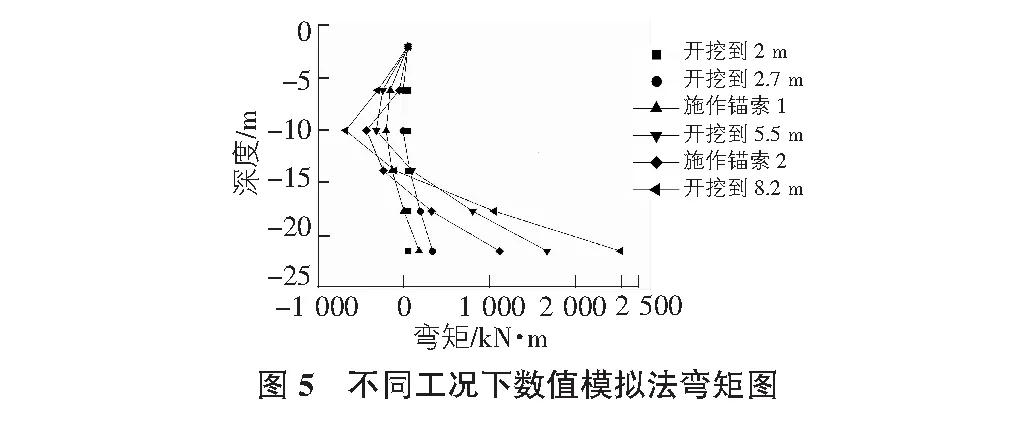
从以上两种方法计算所得的对比图表可以得出以下的规律：

1)分析解析法计算得到的桩身弯矩图可以发现，不同的工况下，桩身的弯矩呈现上部大下部小的S型曲线。原因为：在基坑的开挖过程中，基坑外侧的主动土压力不断增加，而基坑内侧的土被挖走，被动土压力减小，而且桩顶有冠梁和锚索的约束条件，故在基坑的上部呈现向基坑内侧凸出的弯矩曲线；而在基坑的下部，由于基底以下的土层不被挖除，故仍有被动土压力作用在桩的下部，而且被动土压力的增长速度比主动土压力的大，故桩的下部呈现向基坑外侧凸出的弯矩曲线。

表5 两种不同方法计算灌注桩弯矩结果

2)分析数值模拟法计算得到的桩身弯矩图可以发现，不同的工况下，桩身的弯矩符合桩顶自由桩底锚固的抛物线弯矩特点。原因为：在基坑的开挖过程中，基坑外侧的主动土压力不断增加，而基坑内侧的土被挖走，被动土压力减小，而且桩顶有锚索的约束条件，故在基坑的上部呈现向基坑内侧凸出的弯矩曲线；而桩底位于中粗砂层，相当于桩底是锚固的，故会在桩底产生桩端弯矩。总体而言用数值模拟法计算得到的桩身弯矩符合悬臂梁的弯矩分布规律。

3)对比分析解析法和数值模拟法得到的灌注桩桩身弯矩，我们可以发现深度15 m以上的桩身弯矩只有较小的差异；深度15 m以下的桩身弯矩存在较大的差异，这与模型建立时在桩底采用的固端约束有很大的关系。

6 结语

本文分别采用理正深基坑7.0PB4和用MIDAS-GTS对尚东公馆基坑西侧的桩锚支护结构进行位移和弯矩计算，分析总结出了不同计算方法得出的桩锚支护结构的位移和弯矩随不同施工阶段的变化特点。但是由于没有实测数据作为对比数据，所以不能够确定两种计算方法的合理性，这仍需作者本人进一步研究分析，从而验证解析法和数值模拟法对计算桩锚支护结构桩身侧向位移和弯矩的合理性。