基于薄膜比拟的任意截面杆件抗扭惯性矩计算
胡 宽
(同济大学土木工程学院,上海 200082)
0 引言
扭转是结构构件一种常见的受力状态。在针对杆件的扭转分析中,抗扭惯性矩是基本且重要的一个力学特性,对于简单的截面形式(如矩形,圆形,圆环)以及钢结构等薄壁截面,均有较为成熟的计算方法。但是对于非规则的多连通或形状复杂的截面,难以得到抗扭惯性矩的解析解[1]。Prandtl曾提出了薄膜比拟的实验方法,并设计了实验设备,但是操作复杂、测量精度不高。有学者曾提出有限差分法(FDM),该计算方法简单而有效,在单连通截面的分析中应用广泛,但不适合复联通截面[2]。另有研究者针对具体的工程问题,进行简化处理,给出近似解,但不具有通用性[3-7]。在当前计算机有限元分析与智能化设计的潮流下,有必要探索出一种适用性强、可程序化的方法。本文从弹性力学理论出发,基于薄膜理论的思想、有限元方法,提出一种适用于任意复联通截面的高精度计算方法。选取三个算例,证明该方法的通用性与准确性。
1 扭转问题的应力函数理论
1.1 应力函数方程
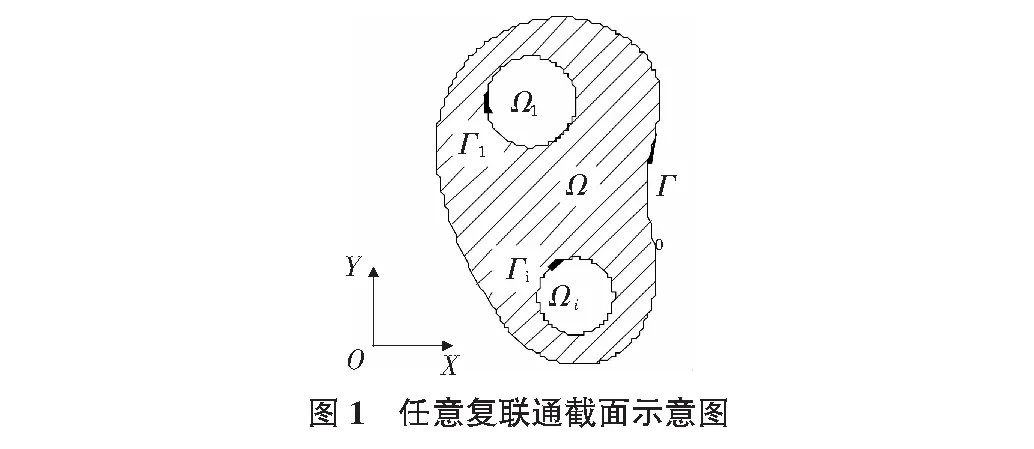
由应力函数理论可得[8],对于图1所示的任意复连通截面形状的杆件在扭转作用下的应力函数方程与边界条件应满足:
(1)
其中,φ为应力函数;G为材料剪切模量;θ为单位长度扭转角;Γi为截面内外边界;Ci为未知常数。应力函数与杆件承受扭矩M应满足:
(2)
其中,Ω为截面域(除去孔洞);Ωi为截面的孔洞。
1.2 薄膜比拟方法
假设有一片张紧的均匀无重力薄膜,受到垂直薄膜平面的均匀压力。可得[9],薄膜的垂度函数z和薄膜变形后与边界平面包围的体积V关系满足:
(3)
(4)
其中,q为薄膜受到的均匀压力;FT为薄膜内张力;Γ为薄膜边界;Ω为薄膜平面域。
若令q/FT=2Gθ,可注意到,薄膜垂度函数与扭转作用下的杆件截面应力函数满足同样的微分方程与边界条件,因此必然具有相同且唯一的解[9],即φ≡z。同理,扭矩M必然等于薄膜与边界平面包围体积的两倍,即M=2V。在物理含义上,应力函数的求解问题可以转化为薄膜垂度函数的计算问题。引入有限单元法的分析思想,借助网格划分算法,即可以得到应力函数的数值解,进而计算抗扭惯性矩。
2 扭转问题的有限元理论
有限单元法分析的一个重要步骤是结构的离散化。本文选取Delaunay三角化方法,该方法可以适应各种边界、多连通域等复杂情况,将任意截面形状离散化为三角形网格。
2.1 基于三角形薄膜单元的有限元列式
根据式(1),应用伽辽金法和变分基本原理,可得:
(5)
令转角θ=-1,假设单元形函数矩阵N,应变矩阵B,单元垂度自由度Ze,则在单元内部Ωe有:
(6)
针对三角形单元,采用一次位移插值形函数,由上式和单元平衡方程KeZe=Pe,推导单元刚度矩阵和荷载列向量为:
(7)
Pe=2GA[1/3 1/3 1/3]T
(8)
其中,A为三角形面积。刚度矩阵中元素为:
kij=bibj+cicj
bi=xj-xm
ci=yj-ym
(9)
其中,xi,yi为三角形单元的节点坐标;i,j,m均为下标轮换,如i→j,j→m,m→i。
2.2 边界条件的处理
对于单联通截面,可以令所有边界上的节点位移为零来求解方程。本论文采用对总体刚度矩阵对角元素改一法处理强制边界条件[10]。当截面存在内环时,应该给内环上所有节点增加位移耦合条件,并将环内以及环上全部荷载移加到环上某一节点,然后令其他环山节点位移等于该节点。由上式可知,环内荷载总和等于2GAi,其中,Ai为内环面积,可用任意多边形的面积计算公式获得[11]。
施加节点位移耦合条件时,应将从节点在总体刚度矩阵中对应的行列元素附加到主节点对应行列上,然后给从节点添加强制边界条件。求解结束后,再将主节点位移赋值给从节点。
3 计算实例
基于C#编程语言实现该计算方法,并针对三个算例进行测试。
对于规则截面(算例1)使用理论公式进行正确性验证;对于非规则工程用截面(算例2,算例3),参考文献[2]的思路,使用ANSYS有限元分析软件建立实体悬臂模型进行验证。选取实体悬臂梁长度L1=50 m,使用Solid95单元,悬臂端连接一个梁单元,长度为L2=1 m,使用Beam188单元。实体单元与梁单元交界处设置刚域(Regid Region)。刚域仅约束X,Y方向(截面平面内)的平动自由度,以避免箱梁的翘曲效应的影响。在梁单元端部施加扭矩T=1 000 kN·m,通过计算实体梁在单位长度内的扭转角,推算抗扭惯性矩。
验证结果表明,该计算方法对于任意复联通截面的扭转惯性矩结果是正确的,且具有相当高的计算精度。算例验证如下。
3.1 圆环截面
计算外径为D=10,壁厚为t的圆环的抗扭惯性矩。其中t分别取0.2,0.5,1三个值。对截面使用Delaunay三角网格化的结果见图2,计算结果与理论值对比见表1。
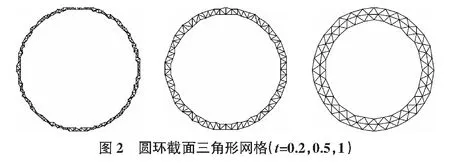
表1 计算结果与误差
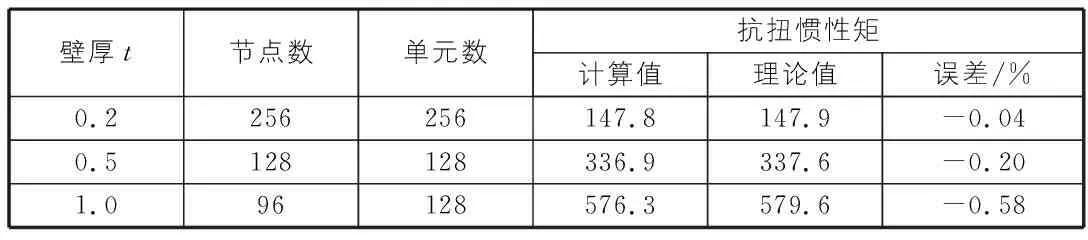
壁厚t节点数单元数抗扭惯性矩计算值理论值误差/%0.2256256147.8147.9-0.040.5128128336.9337.6-0.201.096128576.3579.6-0.58
3.2 单箱室箱型截面
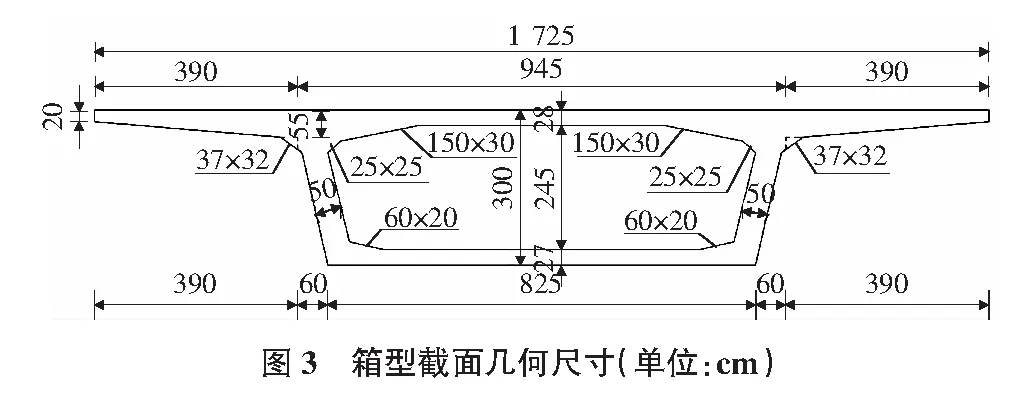
选取截面为箱梁,几何尺寸见图3,三角网格化结果见图4。
在ANSYS中建立实体梁模型见图5,该方法计算结果与ANSYS计算结果对比见表2。

表2 计算结果与误差

节点数单元数抗扭惯性矩/cm4计算值ANSYS误差/%7321 0533.329E+93.461E+9-3.82
3.3 多箱室箱型截面
选取截面为多箱室箱梁,几何尺寸见图6,该方法计算结果与ANSYS计算结果对比见表3。

表3 计算结果与误差

节点数单元数抗扭惯性矩/cm4计算值ANSYS误差/%8591 2031.136E+91.160E+9-2.04
4 结语
基于弹性力学应力函数方程和薄膜比拟方法,可以将任意截面抗扭惯性矩计算问题转化为一维有限元分析问题。
经过验证,该计算方法适用于复联通截面,具有较高的计算精度,可以满足工程需求。通过在C#编程语言上的实现,说明该方法适合程序化应用。

