受拉钢构件可靠指标退化分析

张 华 石 静

(1.中煤西安设计工程有限责任公司，陕西 西安 710054； 2.北京中机一院工程设计有限公司，北京 100044)

工业革命以来，钢铁便被誉为工业社会的骨骼，钢铁工业迅猛发展，2015年我国钢结构建筑用钢量已经达到5 000万t[1]。短短十几年我国钢结构建筑用钢量增加了4 000多万吨，增幅惊人。随着钢结构大量投入使用，钢结构自身所存在的问题也越来越多的暴露出来，钢材抗腐蚀能力差便是其中之一。钢材在潮湿(存在电解质水膜)及空气充足(水中溶有氧)的条件下，容易产生严重的锈蚀损伤，无疑将对建筑物在后续服役期中的抗力和剩余寿命产生重大的影响。目前，我国现行GB 50017—2017钢结构设计规范[2]并未考虑锈蚀对钢材力学性能的影响，认为钢结构在役期间钢构件截面面积及力学性能与设计初期保持一致，而在实际工程中绝大部分钢结构都无法避免锈蚀，在锈蚀作用下，钢材的力学性能和截面面积都会发生相应的变化，而这种变化导致构件的承载能力下降，忽略这种改变而不采取有效的补强措施，必然导致结构损伤不断积累，量变引起质变，最终整个结构破坏。因此研究钢材的锈蚀规律有着十分重要的意义和迫切需要。

1 大气环境下锈蚀钢材的力学性能

为了能很好研究钢材锈蚀后的力学性能，本文采用《金属材料腐蚀试验方法标准汇编》[3]中推荐的户外周期喷淋暴露试验。试验喷剂采用98%的浓硫酸(调整喷剂的pH值在5.7附近)和以硫酸钠为主要成分的工业盐(硫酸钠溶液配比0.2%)两种主要物质调配而成，按规定的间歇时间和喷淋时间将喷剂喷洒在钢试件表面，为使试件正反面锈蚀程度保持一致，每隔一周翻试件一次，试件放在呈45°角的试验摆放装置上，如图1所示。按照试件锈蚀时间，定期将一定数量试件取出，采用一定的技术方法将试件表面锈渣清除干净，自然风干后对其称重。本文采用质量损失率这个指标来评判试件的锈蚀程度，质量损失率的表达式如式(1)所示。

(1)

其中，λ为试件质量损失率,%；m0为试件锈蚀前的质量,g；mt为试件锈蚀一定时间后的质量,g。

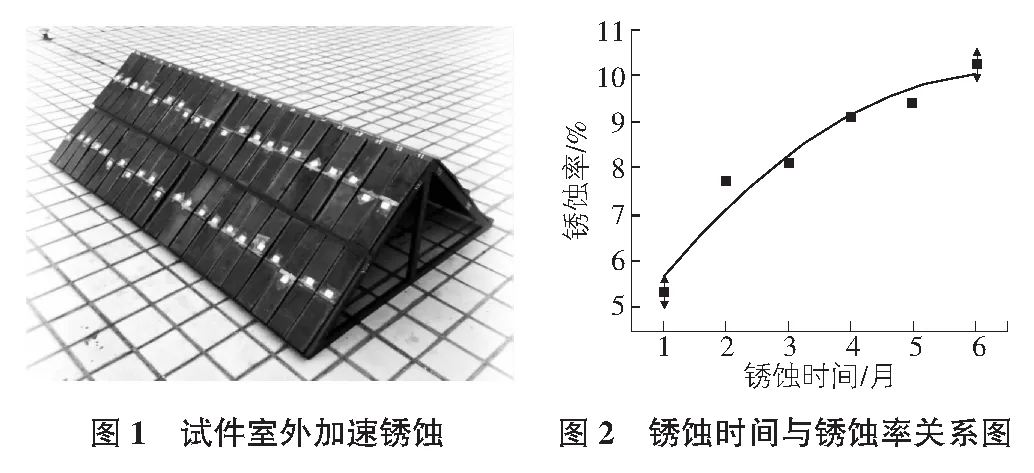
通过对试验结果拟合(见图2)，可以获得锈蚀时间与锈蚀率之间的关系式，如式(2)所示。

dt=3.911+1.893t-0.146t2

(2)

其中，dt为锈蚀率,%;t为锈蚀时间,月。

将锈蚀后试件进行拉伸试验严格按照GB/T 228—2002金属材料室温拉伸试验方法[5]中规定的3 N/mm2·s-1～30 N/mm2·s-1执行(如图3,图4所示)。

根据试验结果，锈蚀试件的屈服强度与未锈蚀试件屈服强度基本保持一致(如图5,图6所示)，假定锈蚀前后试件屈服强度保持不变，则受拉钢构件抗力衰减模型如下。

Rt=fyAt=fyb(d-dt)=fyb(d-3.911-1.893t+0.146t2)。

其中，fy为钢材屈服强度；b为构件宽度；d为构件厚度；t为构件锈蚀时间。

2 受拉钢构件时变可靠指标

2.1 构件功能函数和抗力时变函数建立

根据构件的功能要求和相应极限状态的标志，可建立构件的功能函数或极限状态方程。设X=(x1,x2,…,xn)T是影响构件功能的n个基本随机变量，X可以是构件的几何尺寸、材料的物理力学参数、构件所受作用等，称随机函数Z=g(X)=g(x1,x2,…,xn)为构件的功能函数(或失效函数)。当Z>0表示构件处于可靠状态，Z<0表示构件处于失效状态，Z=0表示构件处于极限状态。对于承受拉力作用的钢构件，其功能函数只有两个随机变量R和S，功能函数如式(3)所示。

Z=g(R,S)=R-S

(3)

相应的极限状态方程为:

Z=g(R,S)=R-S=0

(4)

其中，R为构件抗力；S为构件承受的荷载效应。

上述计算过程中不考虑构件抗力R随时间变化,但是通过上节内容可知钢构件在服役期间由于锈蚀的影响,其截面尺寸及力学性能会随服役时间延长而退化。考虑退化因素后,构件的功能函数如式(5)所示。

Z=g(Rt-S)=Rt-S

(5)

相应的极限状态方程为:

Z=g(Rt,S)=Rt-S=0

(6)

其中，Rt为构件时变抗力。实际上构件在服役期间,其承受的荷载效应S也是随机变量,但不属于本文拟讨论的范围,为节约篇幅假设构件承受荷载效应S服从正态分布。将式(2)代入式(5)得到受拉钢构件抗力时变函数,如式(7)所示。

(7)

2.2 构件时变可靠性指标计算

构件在规定时间内和规定条件下完成预定功能的能力,称为结构的可靠性。构件在规定时间内和规定条件下完成预定功能的概率,称为构件的可靠度[4]。构件可靠度是构件可靠性的概率度量,构件完成预定功能的概率用可靠概率pr表示,相反构件不能完成预定功能的概率用失效概率pf表示。考虑构件功能函数Z为连续随机变量,设Z的概率密度函数为fZ(z),由可靠概率和失效概率的意义可知:

(8)

(9)

设基本随机变量X=(x1,x2,…,xn)T的联合概率密度函数为fX(x)=fX(x1,x2，…，xn),联合累积分布函数为FX(x)=FX(x1,x2,…，xn),则结构的失效概率可表示为:

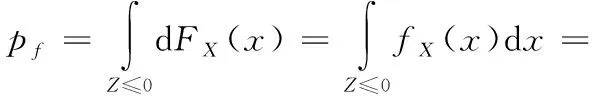
(10)

若各Xi相互独立,Xi的概率密度函数为fXi(xi),则:

(11)

对于式(5)所示构件功能函数g(Rt,S),设Rt和S的联合概率密度函数为fRtS(rt,s),联合累积分布函数为FRtS(rt,s),失效域Ωf简单的以Rt≤S表示,则:

(12)

其中,Rt与S相互独立,其概率密度函数分别为fRt(rt)和fS(s),累积分布函数分别为FRt(rt)和FS(s),则：

(13)

但是基本随机变量的联合概率密度函数一般难以得到,且直接计算多重积分较繁琐,因此通常不用直接积分方法计算式(13),而是通过引入与失效概率有对应关系的可靠指标来评价构件的可靠度。由式(9)可知,构件的失效概率pf取决于功能函数的分布形式,假定分布函数服从正态分布,其均值为μZ,标准差为σZ,则可表示为Z～N(μZ,σZ),此时Z的概率密度函数为:

(14)

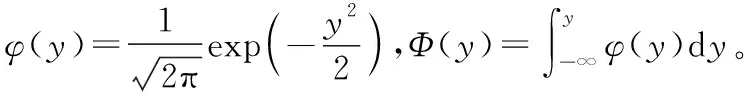
将式(14)代入式(9),此时构件的失效概率为：

(15)

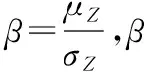
3 锈蚀受拉钢构件可靠指标时变规律

目前,依据GB 50017—2017钢结构设计标准[2]中的规定,认为构件在服役期间其截面面积保持不变;依据GB 50068—2018建筑结构可靠性设计统一标准[6]4.3.8条,对于安全等级为二级的构件延性破坏时其可靠指标β最低要求为3.2。但服役期间的锈蚀作用会导致钢构件可靠指标逐渐衰退,本节就通过锈蚀钢构件受拉承载力可靠指标来揭示这种衰退规律。对宽度为100 mm,厚度为10 mm的钢板进行加速锈蚀,对锈蚀时间不同试件的截面尺寸进行统计分析获得其均值及标准差,Q235级钢材抗拉强度均值和标准分别为μf=340,σf=3.8,承受300 kN拉力时的可靠指标。假设极限状态方程里的参数均服从正态分布,采用改进一次二阶矩法来计算不同锈蚀时间钢构件受拉极限承载力可靠指标β见图7。

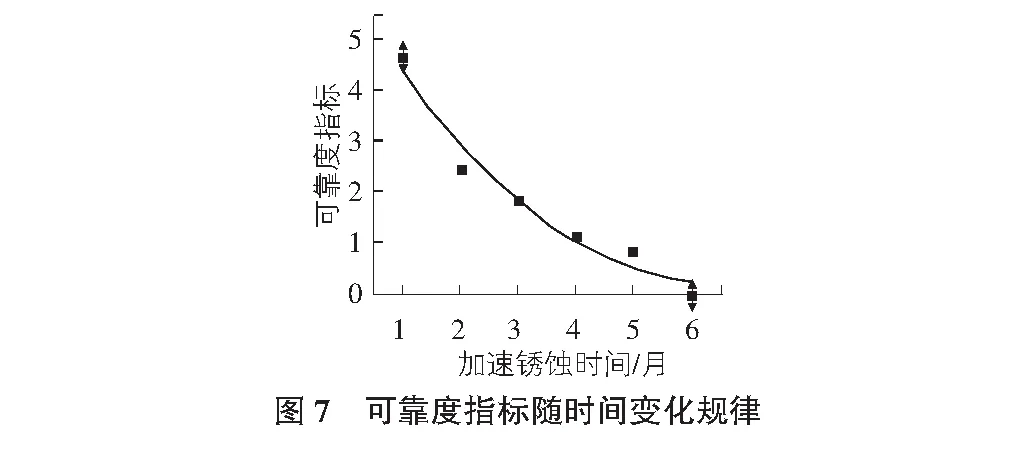
从图7可以看出受拉钢构件的可靠指标并不是一个定值,在锈蚀因素的影响下,该值会随着构件锈蚀程度加剧而不断衰减。当试件加速锈蚀1个月时,其可靠度指标为4.637大于规范限值3.2,此时该构件满足规范要求;而当试件加速锈蚀2个月时,其可靠度指标就已经下降到2.473,小于规范限值3.2,此时构件已经不满足规范的要求;当试件经过6个月的加速锈蚀后期可靠度指标已经降到0.05左右,构件已经丧失承载能力。通过上述内容可以知道,构件的可靠度并不是定值,而是随着构件服役时间的延长、服役环境的影响,构件的可靠指标是在不断衰减,构件失效概率也在逐渐增大,显示出构件的可靠指标具有“时变性”。