试析小学数学解决问题的画图策略

叶晓鹃

摘 要：画图策略指通过画图把抽象问题具体化、直观化，从而搜寻到解题的途径。画图策略可以有效地帮助我们审题、分析、检验。教学中，教师要根据学生的实际需要、知识经验、发展水平，巧妙地运用平面图形、立体图形、单线分段图、复式并列图、形象图、简单示意图等画图策略，把抽象问题具体化、直观化，从而搜寻到解题的途径，提高学生的思维能力与解题能力。

关键词：小学数学;画图策略;解决问题;数学思维

教育心理学研究认为，解决问题的策略是学生认知能力的一个重要方面。在小学阶段，笔者认为画图策略比较符合小学生的思维特征，容易被接受和使用。我们把这种运用画形象的图、线段图、平面立体图等画图的方法理清思路，展示思维的策略，称为“画图策略”，其具有直观性、易懂性、趣味性等特点。教学中，教师要根据学生的实际需要、知识经验、发展水平，巧妙地运用画图策略，提高学生的思维能力与解题能力。

一、画一画，知方法解困惑

空间与图形是小学数学知识的四大领域之一。《空间与图形》的知识与学生的日常生活联系非常密切，都是从生活中抽象出的数学现象，又应用于日常生活中。在学习这一知识时，我们都以让学生动手操作探究为基点，突出探究性学习活动，亲历“做数学”过程，当遇到难题时，我们可以凭借画图辅之解题。

（一）平面图形

有关平面图形的题目中，对于题目中条件比较抽象、不易直接根据所学知识写出答案的问题，教师可以借助画图形帮助思考解题。

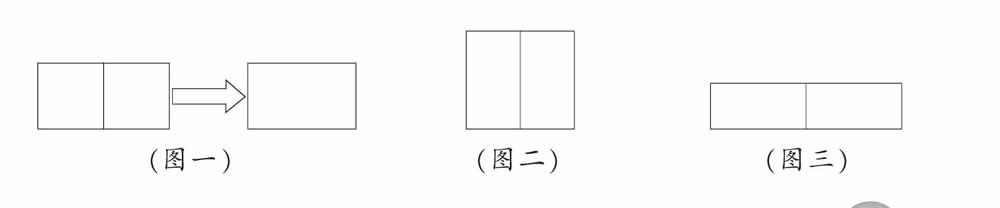
如：“长方形和正方形的周长”是学生比较感兴趣的内容，有这么一道题：把两个边长为5厘米的正方形拼成一个长方形，拼成的长方形周长是多少厘米？（如图一）有些学生脱口而出“40厘米”，而那些没回答的学生，虽然感到有疑问，但又说不出真正的问题所在。刚进入三年级的学生要回答这个问题，确实是存在一定困难的。笔者提醒：你把图画出来看一看呢？于是学生纷纷动笔。

又如，把两个长8厘米，宽4厘米的长方形拼成一个图形，这个图形的周长和面积各是多少？通过画图，学生发现有两种不同的拼法。可以重合变成正方形（如图二），也可以重合得到长方形（如图三）。这两种拼法得到的图形的周长不同，面积相同。学生借助画图的手段，弄清了题中条件的变化，找到了解题的关键，而学生的疑问也在动笔画的过程中解决了。

（二）立体图形

解答一些有关切一切、拼一拼的立体图形题，学生很难理解，也難以想出解题方法。为此教师应该结合题目的内容画出立体图，这样使题目的内容直观、形象，有利于学生思考解题。

如：把一个正方体切成两个长方体，表面积就增加了8平方米。原来正方体的表面积是多少平方米？如果只凭想象，做起来比较困难。而按照题意画图（如图四），可以帮助我们思考，找出解决问题的方法。从图中不难看出，表面积增加了8平方米，实际上是增加2个正方形的面，每个面的面积是8÷2=4（平方米）。原正方体是6个面，即表面积为4×6=24（平方米）。

总之，画图对这道题的解决起到审题和理解题意的作用。对于空间思维比较弱的学生来说，在纸上画画图是解决问题的好策略。画图后，大部分学生一看图就明白了解题方法。画图让题意一目了然，教学效果明显。

二、画一画，明关系释题意

数学教学中，运用线段图的目的不仅仅是帮助学生解决某些具体问题，提高解决问题的能力，更重要的是拓展思维空间。线段图的画法归纳起来一般有两种形式：如果题中的几个量是整体与部分关系时，要画单线分段图;如果几个量是并列关系时，要画复式并列图。

数与代数中的解决问题一直以来是数学学习中的重点与难点，我们不妨用线段图来揭示数学问题中的数量关系，以突破难点。

（一）单线分段图

当学生理解简单的分数应用题时，教师可以借助线段图（单线分段图），帮助理解题中的对应关系。

如：农场有一堆煤共75吨，运走了，还剩多少吨？刚学分数应用题时，学生难以找到剩下的对应分率，很容易将75与相乘，一时无法理解其中的对应关系。但如果画出了以下的单线分段图就一目了然了（如图五）。从图上我们即刻明白与剩下对应的分率是，求剩下的吨数是75×（1-）=30（吨）或者75-75×=30（吨）。

解分数、百分数应用题时，我们可以根据题的内容画图，把题的条件、问题在图上标明，而后再列式。这样有助于学生正确审题，理解题意，从而正确解题，提高我们分析和解决问题的能力。

（二）复式并列图

一些题目条件较多，条件之间关系复杂，学生一时难以解答。可画线段图（复式并列图）表示，寻求解题的突破口。

如：裤子每条28元，每件衣服的价钱是裤子的3倍，每件衣服比裤子贵多少元？这道题目用倍的方法解答学生是比较难以理解的。这时，线段图就起到了一个很好的辅助作用。可以引导学生利用学过的知识画图。

借助线段图的直观作用，学生一下子就列出了“28×（3-1）=56”的算式。就这样，借助一个简单的线段图，很好地引导学生理解了两种数量之间的关系，倍比方法也就在轻松之中迎刃而解了。

总之，符合学生实际的“画线段图”这一探究性学习方法，是数学学习高效的重要手段。当学生百思不得其解时，教师要借助线段图的启发功能引导学生“突破”难点，充分发挥线段图在培养思维能力中的作用，提高学生的思维能力与解题能力。

三、画一画，难变易增兴趣

数学是一门逻辑性很强的学科，我们总是把数学和枯燥联系在一起，实质上，数学也是一门艺术，不仅形象生动同时也具有种种美感。形象图不仅直观、简洁，而且其信息量大，概括性强，有助于记忆。教学中，教师可以让学生在图示和思考过程不断沟通，体会“画图策略”对思维的外显功能及思维对其的依托需求。

（一）简单示意图

如三年级下册《数学广角》中“组合”知识点，“四个人，每两个人互通一次电话，一共需要通几次？”先让学生围绕问题进行操作演习，然后把如何操作的过程用图示表示出来，再结合图形用语言解释，最后用数学算式表达结果。这就让学生经历了把具体事例转换为图示语言，再把思维用语言表达，最后使得抽象思维初步形成。

（二）形象图

笔者曾给三年级的学生上“鸡兔同笼”一课。刚选这一课题时，笔者担心三年级的学生不能理解这一内容。于是，笔者尝试采用了形象教学法，指导学生动笔画，用一个简单的圆形来代替动物的头部，用两根竖线来表示动物的脚。画完后选取部分作品进行展示，并请学生说说自己的想法，很好地满足了学生的表现欲。

总之，数学的学习不拘形式，灵活多变。根据学生的认知规律，学生学习都会经历一个从“外化”到“内化”的过程。学生在画图的过程中，读题、明确问题、寻找条件，把文字转化成图画，发现数量关系，再把图画转成思维，这一系列活动完整地搭建了这个从“外化”到“内化”的过程。解决问题时，我们应巧妙地运用画图策略，以提高学生的思维能力与解题能力。