何时分解加速度
柴守刚

摘要:矢量运算遵循平行四边形定则,在物理解题中,学生往往习惯于力的合成与分解,对于位移、速度、加速度等矢量运算则难以驾驭.在有些物理问题中如果能够抓住加速度这一矢量进行合成与分解,可以大大简化问题的解决,较好地培养学生的思维能力.
关键词:矢量;加速度;正交分解法
加速度是描述物体速度变化快慢的物理量.在动力学物理问题中,应用牛顿第二定律表达式和匀变速直线运动公式时,通常以速度的方向和垂直于速度的方向建立直角坐标系进行列式求解.但在有些问题中该方法显得比较繁琐,如果在解题中根据问题的需要进行合理的分解加速度,不仅可以大大简化问题的解决,而且能够较好地培养学生的思维能力.
1 根据物体的受力情况分解加速度
例1如图1所示,在粗糙水平板上放置一物体,使水平板和物体一起在竖直平面内沿逆时针方向做匀速圆周运动,ab为水平直径,cd为竖直直径.在运动过程中木板始终保持水平,物体相对木板始终静止,则从a到c物体所受木板的摩擦力Ff和木板的支持力FN如何变化?
解题思路 物体与木板保持相对静止一起做匀速圆周运动,物体受到的合力指向圆心.对物体受力分析如图2所示.物体的加速度大小不变,方向总指向圆心.由于物体所受到的力分布在水平和竖直兩个方向上,因此将物体的加速度a按图3所示分解.根据牛顿第二定律mg - FN= ma1,从a到c,a1逐渐增大,则物体所受木板的支持力FN逐渐减小;Ff=ma2,a2逐渐减小,则物体所受木板的摩擦力Ff逐渐减小.
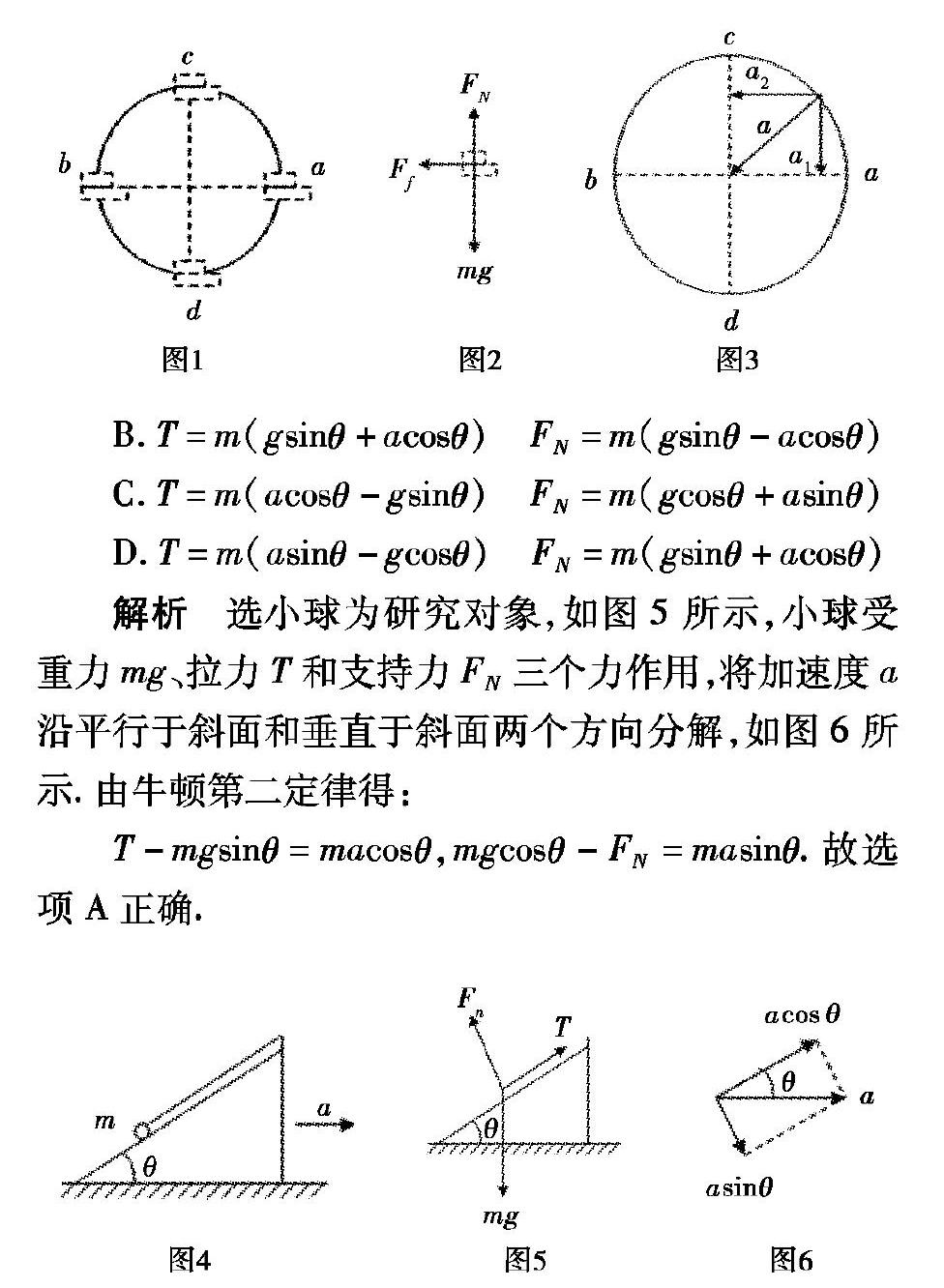
例2如图4所示,细线的一端系一质量为m的小球,另一端固定在倾角为θ的光滑斜面体顶端,细线与斜面平行.在斜面体以加速度a水平向右做匀加速直线运动的过程中,小球始终静止在斜面上.则小球受到细线的拉力T和斜面的支持力FN分别为(重力加速度为g)()
2 根据物体的运动情况分解加速度
例3如图7所示,在倾角为θ的斜面顶端A处以速度vo水平抛出一小球,落在斜面上的某一点B处.设空气阻力不计,求从抛出开始计时,经过多长时间小球离斜面的距离最大?最大距离是多少?
解题思路欲求小球离斜面的最大距离,可将小球的初速度分解为沿斜面的方向和垂直于斜面的方向,如图8所示.根据物体运动的速度情形将加速度也分解为沿斜面的方向和垂直于斜面的方向,如图9所示,根据牛顿运动定律,物体在沿斜面的方向做初速度为v0 cosθ、加速度为gsinθ的匀加速直线运动;在垂直斜面的方向做初速度为vosin0、加速度为gcosθ的匀减速直线运动,当速度为零时,物体离斜面最远.
根据匀变速直线运动规律,在垂直斜面的方向上:
例4 如图10所示,A、B为两个挨得很近的小球,并列放于光滑斜面上,斜面足够长.在释放B球的同时,将A球以某一初速度vo水平抛出,当A球落于斜面上的P点时,B球的位置位于()
A.P点以下
B.P点以上
C.P点
D.条件不足,无法确定
3 整体法受力分析时分解单个物体的加速度
例5如图11所示,重为4N的物体A,被平行于斜面的细线拴在斜面的上端,整个装置保持静止状态.倾角为30°的斜面静止在水平地面上,物体A与斜面间无摩擦.当细线被烧断,物体正在下滑时与静止时比较,斜面对地面的压力( )
A.增加4N
B.减少4N
C.减少1N
D.不变

