多时间尺度时间序列趋势预测

王金策 邓越萍 史明 周云飞

摘 要：针对股票、基金等大量时间序列数据的趋势预测问题，提出一种基于新颖特征模型的多时间尺度时间序列趋势预测算法。首先，在原始时间序列中提取带有多时间尺度特征的特征树，其刻画了时间序列，不仅带有序列在各个层次的特征，同时表示了层次之间的关系。然后，利用聚类挖掘特征序列中的隐含状态。最后，应用隐马尔可夫模型（HMM）设计一个多时间尺度趋势预测算法（MTSTPA），同时对不同尺度下的趋势以及趋势的长度作出预测。在真实股票数据集上的实验中，在各个尺度上的预测准确率均在60%以上，与未使用特征树对比，使用特征树的模型预测效率更高，在某一尺度上准确率高出10个百分点以上。同时，与经典自回归滑动平均模型（ARMA）模型和PHMM（Pattern-based HMM）对比，MTSTPA表现更优，验证了其有效性。

关键词： 特征树;时间序列预测;多时间尺度趋势预测;隐马尔可夫模型

中图分类号： TP181

文献标志码：A

文章编号：1001-9081（2019）04-1046-07

Abstract： A time series trend prediction algorithm at multiple time scales based on novel feature model was proposed to solve the trend prediction problem of stock and fund time series data. Firstly， a feature tree with multiple time scales of features was extracted from original time series， which described time series with the characteristics of the series in each level and relationship between levels. Then， the hidden states in feature sequences were extracted by clustering. Finally， a Multiple Time Scaled Trend Prediction Algorithm （MTSTPA） was designed by using Hidden Markov Model （HMM） to simultaneously predict the trend and length of the trends at different scales. In the experiments on real stock datasets， the prediction accuracy at every scale are more than 60%. Compared with the algorithm without using feature tree， the model using the feature tree is more efficient， and the accuracy is up to 10 percentage points higher at a certain scale. At the same time， compared with the classical Auto-Regressive Moving Average （ARMA） model and pattern-based Hidden Markov Model （PHMM）， MTSTPA performs better， verifying the validity of MTSTPA.

Key words： feature tree; time series prediction; trend prediction at multiple time scales; Hidden Markov Model （HMM）

0 引言

伴隨着金融行业的快速发展，产生了大量垂类数据，如股票价格序列、期货价格序列以及各类基金价格序列等时间序列数据[1]，因此，金融时间序列预测已经得到了广泛的研究[2]。现有预测算法主要通过时间序列回归分析，实现单一时间尺度上的点预测，忽略了多时间尺度的趋势预测。多时间尺度趋势预测对于金融投资等领域中的应用具有重要意义。投资者往往需要预测金融产品在未来以日、周、月和季度为周期等不同时间尺度下的价格走势，从而设计最优的投资策略。时间序列的多时间尺度趋势预测，不仅强调时间尺度的层次性（即大时间周期由若干小时间周期组成），还强调对特定时间尺度上的某个趋势的开始和结束时间进行预测。

实现股票时间序列的多时间尺度趋势预测的挑战在于如何准确、全面地提取时间序列中的多时间尺度特征。本文对此进行了研究，主要思路是，通过提取有效的时间序列多时间尺度的层次特征，建立基于特征树的隐马尔可夫预测模型。基于这一思路，本文主要做了如下工作：1）提出了一种有效的时间序列多时间尺度特征模型──特征树。特征树的每一层对应一个时间尺度，越接近根结点，时间尺度越大。特征树中的每个结点代表一个特定时间尺度下的时间序列分段。特征树刻画了原始时间序列数据在多时间尺度上的层次性以及层次之间的联系。

2）提出了基于特征树的多时间尺度趋势预测算法MTSTPA（Multiple Time Scaled Trend Prediction Algorithm）。MTSTPA能同时对不同尺度下的趋势以及趋势的长度作出预测。MTSTPA将特征树的每个层次的特征子树序列视为该层时间尺度下的观测序列，从中学习得到该时间尺度下的隐马尔可夫模型（Hidden Markov Model， HMM），从而实现该层时间尺度下的趋势预测。此外，为了提高预测精度，MTSTPA在作出预测之前，首先对噪声进行了过滤。

3）在真实数据集上验证了本文提出的模型和算法的有效性。

1 相关工作

本文的相关工作包括时间序列特征提取、状态挖掘和时间序列预测。

1）特征提取：文献[3-4]提取时间序列的形态特征，文献[5-6]提取时间序列的频率特征，文献[7]获取序列自相关系数，文献[8]提取序列的频繁模式等。

提取形态特征一般做法是对时间序列单层次分段，并用长度、斜率、点到线段的距离等作为每个分段的特征。提取频率特征主要途径是在单一时间尺度内将时间序列分解为一组正交的频域基函数的线性组合（如傅里叶变换），将分解得到的各项系数作为频率成分。使用时间序列的自相关系数、偏相关系数等特征，可以确定影响当前数值的历史数据的个数。时间序列符号化会在一定程度上造成数据损失，而提取频繁模式同样是属于时间序列单一尺度上的特征。上述特征提取方法的不足之处是没有考虑时间序列的多时间尺度特征，因此有必要提出新的特征模型。

2）状态挖掘。文献[9]提出了基于时间序列形态的隐藏状态转移模型，其缺点是只针对序列的单一时间尺度的状态。文献[10]提出了一种基于概率的全局状态转换模型，对时间序列进行多层次分段，但是不能实现单一时间序列在多时间尺度上的状态发现。

3）时间序列预测。常见的时间序列预测模型包括滑动平均模型、利用指数平滑预测模型[11]、自回归滑动平均模型（Auto-Regressive Moving Average Model， ARMA）、基于特征变换的神经网络预测模型[12-13]、基于拓扑结构的TPM（Topology Preserving Map）模型[14-15]和贝叶斯网络模型，以上预测模型均根据序列的部分历史数据，预测下一个时间点或时间段的具体数值。

文献[9]在隐马尔可夫模型的基础上得到PHMM（Pattern-based HMM），仅仅对单一时间尺度趋势预测作出了研究，没有实现对金融时间序列多时间尺度趋势的预测。

2 特征树模型

2.1 时间序列分段

一条时间序列可以根据趋势的变化划分为一系列的线段，这些线段是构成时间序列特征树的基本元素。由于时间序列充满噪声，为了降噪，在划分线段之前，本文首先应用文献[11]中差离值（DIFferential value， DIF）对原始序列进行滤波，在此基础上，在大小预先设置的滑动窗口内，应用最小二乘法拟合一条线段，并根据各个窗口内线段斜率的变化，判断序列中的极值点，两个相邻极值点之间的连线即为一个分段。分段過程如算法1所示。

算法1 时间序列分段。

算法1中：第3）行DIF（）将v转换为DIF; time表示当前时刻的索引; flag表示当前段是否结束;tsh衡量拟合斜率是否有效;第5）行CurrentSlope表示OLS（）应用最小二乘法获取当前滑动窗口内数据的拟合斜率;第7）行判断是否产生一个极值点（LastSlope表示上一个窗口内数据的拟合斜率，初始值为1）。

设置tsh是为了防止序列在窗口内的微小波动影响分段效果，其大小根据拟合斜率的分布（在历史数据中统计得出）设置，如图1所示（斜率的概率分布图）。本文实验数据集上的拟合斜率服从高斯分布，且均值为0，设置tsh为此分布的51%的分位数μ0.51，在区间[-μ0.51， μ0.51]内的拟合斜率视为无效斜率，不具有趋势特征。

2.2 特征树定义

设时间序列F有H种时间尺度的分段，即有H个不同层次的表示。原始序列的相邻极值点之间的连线代表其最小尺度分段，第一个极值点与末尾极值点之间的连线代表最大尺度分段。记时间序列在h层上的分段序列为：F（h）=（f（h）1， f（h）2，…， f（h）n），1 ≤ h ≤ H，1 ≤ n ≤ 2h-1，F（h）表示时间序列的第h层， f（h）i（1 ≤ i ≤n） 表示h层第i个分段。

图2（横坐标为极值点对应的时间）展示了一个时间序列三层分段示例：

第一层只有一根线段，代表最大的时间尺度;第三层为代表最小时间尺度的分段序列，包含4个分段，每个分段通过连接原始序列相邻极值点得到。

图3给出了图2所示时间序列对应的特征树。每棵特征树都带有表示层次之间联系的特征，根结点代表最大尺度，区间长度为29，其趋势由两棵子树确定，左右代表时间的先后同时左右子树分别由各自的子树构成。因此，特征树完整刻画了时间序列在各个层次上的趋势表现，同时也表示了每个层次之间的联系。

2.3 特征树生成

特征树生成是将时间序列压缩为一棵树的过程。生成过程为动态增长：时间序列的每一段作为底层叶结点，每两段组合为一段，生成父结点，计算其斜率和区间并记录，新的一层继续向上增长，直至最高层结点数为1。

由于特征树生成过程中底层结点的个数不一定为2n，例如，m层结点个数为奇数，则说明此时在尺度m+1下没有新的分段。因此，当某层结点个数为奇数时停止生长，等到本层有新结点加入继续向上更新。本文算法每层用一个链表辅助特征树的生成。构造特征树的具体过程如算法2～3所述。

算法2 特征树生成。

算法3中：Mcount表示T的m层的结点个数;Node表示T的一个新结点;NewList表示T新一层的链表;T（m）MCount表示时间序列在尺度m下的特征子树链表中的第MCount个结点;T的每个结点保存着对应尺度下每个分段的斜率，长度和左右子树，其层数是时间序列特征树的层数，同时T的每一层构成某一尺度下的特征子树链表。

3 预测模型

文献[9-10]为应用隐马尔可夫模型预测时间序列状态提供了思路。时间序列在某个尺度下的一个分段，作为本尺度特征子树的根结点，本研究基于时间序列的各个时间尺度下的特征子树序列，分别训练一个相应时间尺度下的隐马尔可夫模型（HMM），不同的时间尺度的特征子树序列分别对应HMM，基于HMM的解码功能即可实现原始时间序列的多时间尺度预测。

3.1 观测序列

本文将时间序列中各时间尺度下的特征子树序列视为观测序列。h尺度下的观测序列表现为以特征树的第h层结点为根结点的特征子树的序列，T（h）=（T（h）1，T（h）2，…，T（h）n），n表示h层有n棵特征子树。

3.2 状态发现

首先，文献[9]中证明，时间序列中存在不同分布，由此通过聚类分析确定一个特征子树序列中隐藏的状态。

1）相似性度量。

图4所示特征树的第二层有两棵特征子树，每棵特征子树由三个结点（1个根结点和2个子结点）构成，这两棵特征子树构成一个特征子树序列，表示了时间序列在尺度2下的观测特征。

现在的任务是对特征子树序列T（h）中的子树聚类。首先将每个结点的两个属性值用离差标准化方法（min-max normalization）归一化，如式（1）所示：NorV=value-MinVMaxV-MinV（1）

其中：value为待归一化数据值;MinV和MaxV分别为相同位置上最小值和最大值。

特征树中的结点对时间序列趋势的影响按照层次由低到高依次减小，故给特征树的每层分配权重1/H，每层结点则均分1/H的权重。以图4表示的特征树为例，每层平均占有1/3的权重，第二层的每个结点占有（1/3）/2，第三层四个结点则每个结点占有（1/3）/4。每个结点的权重函数定义如下：weight（h）=1H×2h-1（2）

其中：h为特征树第h层。两棵子树的相似性度量函数定义如下：

其中：count（s）统计状态序列Q（h）中出现子序列s的次数。

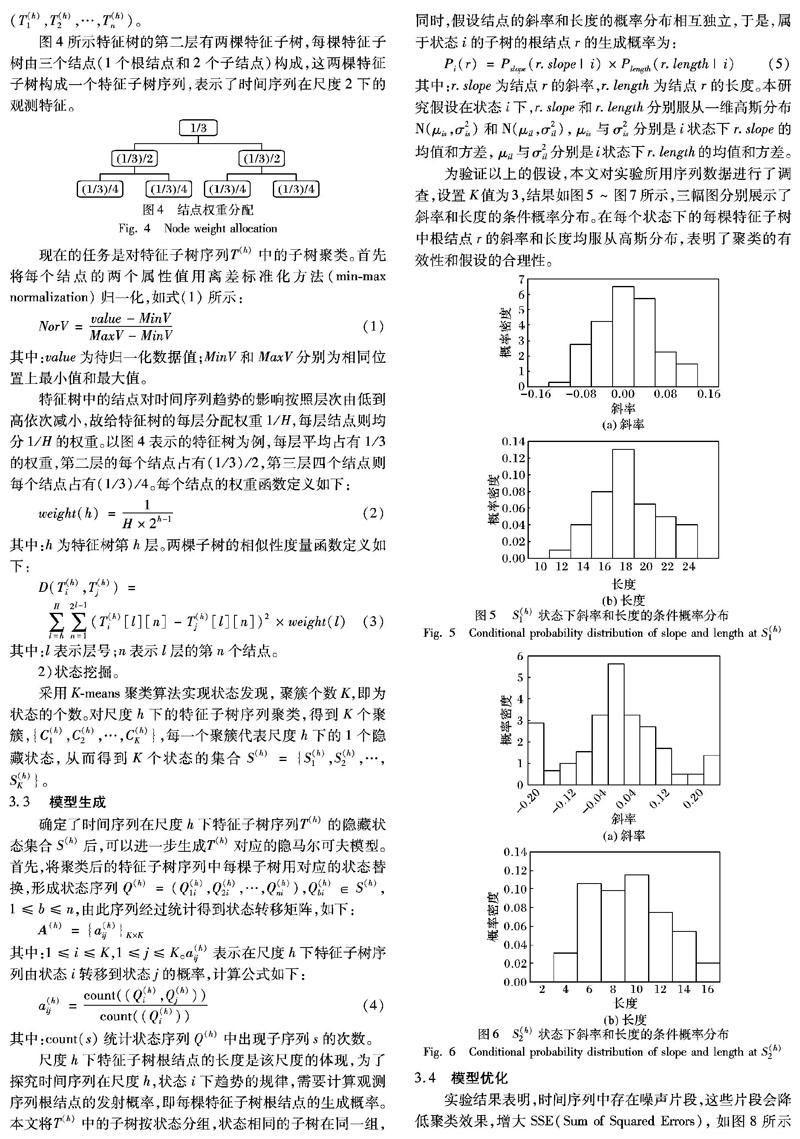
尺度h下特征子树根结点的长度是该尺度的体现，为了探究时间序列在尺度h，状态i下趋势的规律，需要计算观测序列根结点的发射概率，即每棵特征子树根结点的生成概率。本文将T（h）中的子树按状态分组，状态相同的子树在同一组，同时，假设结点的斜率和长度的概率分布相互独立，于是，属于状态i的子树的根结点r的生成概率为：

为验证以上的假设，本文对实验所用序列数据进行了调查，设置K值为3，结果如图5～图7所示，三幅图分别展示了斜率和长度的条件概率分布。在每个状态下的每棵特征子树中根结点r的斜率和长度均服从高斯分布，表明了聚类的有效性和假设的合理性。

3.4 模型优化

实验结果表明，时间序列中存在噪声片段，这些片段会降低聚类效果，增大SSE（Sum of Squared Errors），如图8所示（横坐标为滑动步数d），随着噪声片段按照一定步长向前滑动，SSE随着d增长逐渐减小后有上升趋势。

为解决这一问题，本研究通过预先对原始时间序列数据去噪实现对模型的优化。假设现有时间序列，N个数据点。用4个时间点start、 p、q、end将其分为三段L1（start： p），L2（p： q），L3（q： end）。设置初始值p=0，q= p+U，设置一个长度为U的噪声窗口，即L2。合并L1与L3两段数据，利用算法1分段，再用K-means聚类，得出SSE。完成一次SSE计算后， p与q向右滑动step个数据，即p= p+step，q=q+step，循环计算SSE，直到窗口滑动至末尾。

SEE越小聚类效果越好，根据上述执行结果，确定使SSE最小的窗口位置为最佳噪声片段位置，即p值。具体过程如算法4所示。

算法4中：GetSSE（）是得到聚类结果的SSE;SL为分段结果链表。

4 预测模型MTSTPA

由于每个时间尺度下的特征子树根结点表示该尺度下一个分段的斜率和长度，本文算法MTSTPA通过该特征子树序列的HMM序列预测下一棵子树根结点。

由3.3节得出，时间序列在尺度h下对应状态转移矩阵A（h），根据A（h）得到下一个出现概率最大的状态i。根据3.3节得出，在处于相同状态的特征子树集合中，特征子树根结点的斜率和长度相互独立，且分别服从高斯分布，又根据式（7）得出，在某个状态i下，当根结点的slope与length全部取均值时概率最大。因此，状态i对应聚簇的簇中心为最优预测值。由此本文提出一个多时间尺度预测算法MTSTPA。MTSTPA在极值点处作出预测，如果当前点不能确定为极值点，则根据时间序列的上一个极值点，预测序列当前所处的趋势。MTSTPA对时间序列在尺度h下的趋势的预测过程如算法5所示。

算法5 MTSTPA。

其中： MinV与MaxV分别是对应原数据的最小值与最大值。

5 实验

在2001年01月01日至2015年07月08日時间段内，深交所和上交所的每支股票每日收盘价数据都会构成3600个数据点的时间序列，本研究取所有股票的时间序列作为实验数据集。每条时间序列的前70%作为训练数据，后30%作为测试数据。本文使用下式定义的预测精度作为评价指标：

为了验证本文提出的特征树模型、预测模型和预测算法MTSTPA的有效性，本文设计了五组实验：第一组，验证分段算法;第二组，确定预测模型参数，即隐马尔可夫模型状态数K与优化模型噪声窗口大小U;第三组，特征树模型有效性验证;第四组，模型优化验证;第五组，与传统预测模型多时间尺度预测精度对比。每组预测实验进行三次，取三次预测精度的平均值。每次实验在数据集中随机选取20条序列作为实验数据。

5.1 验证分段算法

为验证算法1的有效性，实验比较了原始时间序列与由算法1得出的极值点序列对应时间段的趋势。图9表示一条原始时间序列，将其作为输入数据执行算法1得到极值点序列，如图10所示。

原始时间序列1～7下降趋势，7～9上升趋势，9～14下降趋势，14～29是上升趋势，与图10中极值点之间线段的趋势相同，验证了算法1对极值点判断的准确性。

5.2 参数的选择

通过实验确定隐藏状态的个数K（K-means聚类的聚簇个数）。

根据MTSTPA预测时间序列在多个时间尺度内的趋势。K分别取2、3、4，尺度n=3开始预测（特征树第三层开始有四棵子树），预测结果如图11所示，在实验所用数据集上，K=3时各个时间尺度上的预测精度均大于55%，最高可达到75%以上，因此K取值为3。

通过实验确定U/N。设计实验：分别取U/N×100%值为15%、25%、35%、45%、55%，统计每个值对应实验的预测精度，对比得出最优U/N。

图12显示，在实验所用数据集上，噪声窗口占总数据35%时各个时间尺度的预测精度均在65%以上。因此优化模型将长度占总数据35%的数据片段视为噪声片段，应用算法2找出片段最佳位置，将其滤除。

5.3 特征樹有效性

实验用两个策略进行对比验证：策略1，未使用特征子树，用树的单层结点序列（对应时间尺度的分段序列）作为本时间尺度的观测序列;策略2，使用特征子树，用该时间尺度下的特征子树序列作为观测序列（本文所用策略）。实验设置K=3，U/N=35%。如图13所示，策略2在各个时间尺度下的预测精度均优于策略1，其中尺度4和尺度5高出10个百分点以上，验证了策略2的有效性。

图13显示，预测精度随着时间尺度的减小由增加到下降，分析得出模型的预测精度与两个因素相关：1）每个时间尺度下的特征子树的棵数;2）每棵特征子树所携带的层次信息的多少。在本组实验中，尺度3到尺度5，时间尺度依次减小，特征子树个数依次增多，故通过式（6）统计得到的A（3）、A（4）与A（5）准确度依次增高，预测精度逐渐达到最高79%;尺度5到尺度9下的特征子树携带的层次信息逐渐减少，预测精度下降，但是最低预测精度仍在55%以上。

5.4 模型优化验证

为了验证优化模型的有效性，现进行优化前后预测精度对比实验。实验设置K=3，U/N=35%。图14显示了优化前后的预测效果。优化模型预测精度总体上优于优化前模型，验证了优化算法的有效性。

5.5 MTSTPA有效性

本组实验对比MTSTPA、ARMA与PHMM三种时间序列预测模型的预测精度。PHMM同样应用隐马尔可夫模型，采用单纯分段特征，预测单一时间尺度下序列走势。实验设置MTSTPA参数K=3，U/N=35%。针对多时间尺度预测，为使实验结果具有说服力，在给定时刻t，预测t+Δt时刻的趋势，其中，Δt代表不同的时间尺度。实验中选取Δt=5，10，20，40，80，160。

图15显示了三种模型的预测精度。MTSTPA在每个预测步长的表现都优于其他两种模型。ARMA作为经典的时间序列预测模型可以预测短时期的数据，但是难以捕捉时间序列在不同时间尺度下的特征。PHMM每段特征属性只包含slope与length，没有包含层次特征。ARMA和PHMM的多步预测方法是根据之前的预测值对后续值进行预测，而MTSTPA是根据特征树捕捉到的各时间尺度下的特征在所有时间尺度上的预测。因此，在多时间尺度趋势预测方面，MTSTPA优于其他两种模型。

6 结语

本文提出了一种新的特征模型──特征树。特征树刻画了原始时间序列数据在多时间尺度上的层次结构以及各层次之间的联系。在此基础上，本文提出了基于特征树的多时间尺度趋势预测算法MTSTPA，该算法将对应时间尺度的特征子树序列视为观测序列，从中学习得到一个HMM，利用HMM的预测功能实现不同时间尺度上的趋势预测。但是，本文算法对频繁震荡的序列数据无法有效预测，因此采用自适应的聚类算法和概率图模型解决此类问题是下一步的研究重点，另外本文研究时间序列的趋势预测，未来将研究多时间尺度的时间序列点预测。

参考文献（References）

[1] 张普， 吴冲锋. 股票价格波动： 风险还是价值？[J]. 管理世界， 2010（11）： 52-60. （ZHANG P， WU C F. Stock price volatility： risk or value [J]. Management World， 2010（11）： 52-60.）

[2] 唐黎.金融时间序列预测的信息融合与计算智能模型[D]. 成都： 电子科技大学， 2018： 1-4. （TANG L. Information fusion and computational intelligence models for financial time series prediction[D]. Chengdu： University of Electronic Science and Technology of China， 2018： 1-4.）

[3] KEOGH E， CHU S， HART D， et al. An online algorithm for segmenting time series [C]// Proceedings of the 2001 IEEE International Conference on Data Mining. Piscataway， NJ： IEEE， 2001： 89-296.

[4] CHANG P C， LIAO T W， LIN J J， et al. A dynamic threshold decision system for stock trading signal detection [J]. Applied Soft Computing， 2011， 11（5）： 3998-4010.

[5] 梁强， 范英， 魏一鸣. 基于小波分析的石油价格长期趋势预测方法及其实证研究[J]. 中国管理科学， 2005， 13（1）： 30-39. （LIANG Q， FAN Y， WEI Y M. Long term trend forecasting method of oil price based on wavelet analysis and empirical study [J]. Chinese Journal of Management Science， 2005， 13（1）： 30-39.）

[6] MORCHEN F. Time series feature extraction for data mining using DWT and DFT [EB/OL]. [2018-05-10]. http：//mybytes.de/papers/moerchen03time.pdf.

[7] SUN Y Q， WANG R J， SUN B Y， et al. Prediction about time series based on updated prediction ARMA model [C]// Proceedings of the 2013 10th International Conference on Fuzzy Systems and Knowledge Discovery. Piscataway， NJ： IEEE， 2013： 680-684.

[8] ZHANG D E H， LI G C L， WONG A K C. Discovery of temporal associations in multivariate time series [J]. IEEE Transactions on Knowledge and Data Engineering， 2014， 26（12）： 2969-2982.

[9] WANG P， WANG H X， WANG W. Finding semantics in time series[C]// Proceedings of the 2011 ACM SIGMOD International Conference on Management of Data. New York： ACM， 2011： 385-396.

[10] HAN Z， CHEN H F， YAN T， et al. Time series segmentation to discover behavior switching in complex physical systems [C]// Proceedings of the 2015 IEEE International Conference on Data Mining. Piscataway， NJ： IEEE， 2015： 161-170.

[11] CREAMER G， FREUND Y. Automated trading with boosting and expert weighting [J]. Quantitative Finance， 2009， 10（4）： 401-420.

[12] KAASTRA I， BOYD M. Designing a neural network for forecasting financial and economic time series [J]. Neurocomputing， 1996， 10（3）： 215-236.

[13] ZIAT A， DELASALLES E， DENOVER L， et al. Spatio-temporal neural networks for space-time series forecasting and relations discovery[C]// Proceedings of the 2017 IEEE International Conference on Data Mining. Washington， DC： IEEE Computer Society， 2017： 705-714.

[14] DANELMAYR G， GADALETA S， HUNDLEY D， et al. Time series prediction by estimating Markov probabilities through topology preserving maps[EB/OL]. [2018-05-10]. https：//doi.org/10.1117/12.367685.

[15] 王雙成， 高瑞， 杜瑞杰. 具有超父结点时间序列贝叶斯网络集成回归模型[J]. 计算机学报， 2017， 40（12）： 2748-2761. （WANG S C， GAO R， DU R J. With super parent node Bayesian network ensemble regression model for time series[J]. Chinese Journal of Computers， 2017， 40（12）： 2748-2761.）

[16] BOX G， JENKINS G， REINSEL G， et al. Time Series Analysis： Forecasting and Control[M]. New York： Wiley， 2015： 2-17.