基于小波变换的分数阶微分算法在肝脏肿瘤CT图像纹理增强中的应用

邱甲军 吴跃 惠孛 刘彦伯

摘 要：图像纹理增强过程中容易丢失平滑区域纹理细节，而分数阶微分增强虽然能够非线性保留平滑区域纹理细节，但对频率分辨率敏感。针对这个问题，提出一种基于小波变换的分数阶微分纹理增强算法，应用于平扫计算机断层扫描（CT）图像的肝脏肿瘤区域的纹理增强。首先，通过小波变换将图像感兴趣区分解成多个子带分量;其次，基于分数阶微分定义构造一个带补偿参数的分数阶微分掩膜;最后，使用该掩膜与每个高频子带分量进行卷积并利用小波逆变换重组图像感兴趣区。实验结果表明，该方法在使用较大分数阶次显著增强肿瘤区域的高频轮廓信息的同时，有效地保留了低频平滑的纹理细节：增强后的肝细胞癌区域与原区域相比，信息熵平均增加36.56%，平均梯度平均增加321.56%，平均絕对差值平均为9.287;增强后的肝血管瘤区域与原区域相比，信息熵平均增加48.77%，平均梯度平均增加511.26%，平均绝对差值平均为14.097。

关键词：纹理增强;小波变换;分数阶微分;肝细胞癌;肝血管瘤;计算机断层扫描图像

中图分类号：TP391.4

文献标志码：A

文章编号：1001-9081（2019）04-1196-05

Abstract： Smooth texture details are easily lost in the process of image texture enhancement. Although fractional-order differential enhancement can preserve the texture details of smooth regions nonlinearly， it is sensitive to frequency resolution. Focusing on this problem， a fractional differential texture enhancement algorithm based on wavelet transform was proposed and applied to texture enhancement of liver tumor regions in plain Computed Tomography （CT） images. Firstly， wavelet transform was used to decompose the image region of interest into multiple subband components. Then， a fractional differential mask with compensation parameter was constructed based on fractional-order differential definition. Finally， the mask was used to convolve with each high frequency subband component respectively， and the image region of interest was recombined by using reverse wavelet transform. The experimental results show that the algorithm effectively preserves the low-frequency smooth texture details while observably enhances the high-frequency contour information of the tumor region by a relatively large fractional order： compared with the original region， the enhanced hepatocellular carcinoma region has the information entropy increased by 36.56% averagely， the average gradient increased by 321.56% averagely， and the mean absolute difference of 9.287 averagely; compared with the original region， the enhanced hepatic hemangioma region has the information entropy increased by 48.77% averagely， the average gradient increased by 511.26% averagely， and the mean absolute difference of 14.097 averagely.

Key words： texture enhancement; wavelet transform; fractional differential; hepatocellular carcinoma; hepatic hemangioma; Computed Tomography （CT） image

0 引言

在医学图像处理中，纹理是放射组学中一种重要的定量数据特征，丰富的纹理代表了大量非可视数据[1]。在肝脏肿瘤的计算机辅助诊断系统中，基于计算机断层扫描（Computed Tomography， CT）图像纹理的分类识别是一种可行的辅助诊断方法[2]，但CT扫描中不同的参数设置、容积效应，以及病灶本身在病理组织上的复杂性，使得感兴趣区的图像解释比较困难，因此纹理增强成为放射组学中模式识别、图像恢复等诸多领域的一种重要手段[3-4]。另外，造影剂增强的CT作为常用的检查方法可能引起肾毒性和过敏反应[5-6]，本文采用平扫CT图像进行纹理增强研究。

图像纹理增强方法主要分为变换域和空间域两大类。变换域方法中，小波变换的多分辨率分析特点使其在医学图像此类非平稳信号的纹理增强中被广泛应用[7]：2012年Bhardwaj等[8]基于Haar小波变换结合软阈值法对腹部CT与X射线图像进行处理，增强了图像细节并保留了图像中的边缘;2016年Lavanya等[9]基于对偶树实小波变换与中值滤波相结合，对被高斯等噪声影响的X射线乳腺图像进行恢复与增强处理，获得了较好的峰值信噪比。空间域方法中，分数阶微分能够在提高图像高频信息的同时，非线性保留低频信息，近年来被较多地应用于医学图像纹理增强中[10-11]：2013年Jalab等[4]构造基于广义分数算子的二维各向同性梯度掩模对脑部磁共振（Magnetic Resonance， MR）图像进行纹理增强研究，提取到图像细节信息并突出显示图像中的边缘;2015年Li等[12]提出自适应分数阶微分对腹部CT、B超、MR等图像进行增强，使图像获得了更加清晰的边缘以及更加丰富的纹理;2016年陈向阳等[13]基于局部的熵、梯度、方差提出自适应分数阶微分掩膜，对CT、MR等图像进行处理，获得较好的视觉效果。

本研究以小波变换的多分辨率分析方法为基础，结合分数阶微分的定义构造了一个带补偿参数的微分掩膜，提出一种基于小波变换的融合算法，对平扫的肝脏肿瘤CT图像进行纹理增强研究，并基于熵、平均梯度、平均绝对差等参数对增强效果进行了评估。

1 数据与方法

在肝脏肿瘤中，两类常见的恶性与良性肿瘤分别是肝细胞癌（Hepatocellular Carcinoma， HCC）与肝血管瘤（Hepatic Hemangioma， HEM）。本文选择了四川大学华西医院2015年1月1日至2016年10月31日的129例HCC和2013年1月1日至2016年10月31日的140例HEM进行了回顾性研究。CT图像由Siemens SOMATOM Definition AS+CT设备、Philips Brilliance 64 CT设备、或Siemens SOMATOM Definition CT设备扫描获得，扫描层厚均为5mm，分辨率为512×512，窗值为35～60，窗宽为200～350，以平扫期图像作为纹理增强对象，动脉期图像与门脉期图像分别作为诊断与分析的参考。

变换域方法是对图像变换过程中的变换系数进行某种修正（直接影响到增强效果），然后再进行逆变换实现图像纹理增强。基于空间域的增强方法是对像素直接进行操作，常见方法有直方图均衡、差分掩模等。在直方图均衡法中，图像对比度提升的程度严重依赖于频数的分布，可能使增强后的图像出现过暗、过亮，以及伪轮廓等问题。广泛使用的Sobel、Prewitt、Laplacian等整数阶差分掩膜能够较好地增强图像高频边缘纹理信息，却大幅线性衰减了灰度变化较小的纹理细节，分数阶微分弥补了这一缺陷。本文拟提出一种小波融合算法，结合小波变换多分辨率分析的优势与分数阶微分的优势，对平扫的肝脏肿瘤CT图像进行纹理增强研究。

1.1 图像预处理

为了使得对熵、平均梯度、平均绝对差等的评估能够更加准确反映纹理增强在计算机辅助诊断肝脏肿瘤中的价值，本文仅对肿瘤区域进行熵的计算。在每个病例中选择CT平扫期图像中、肿瘤截面积相对较大的一张图像，并在被选择图像的肿瘤区域内部截取一个面积尽可能大的矩形。

1.2 小波变换

小波变换[14-15]将信号表示为由基本函数平移与缩放而成的一簇函数的线性组合。离散化后的一维小波变换容易扩展到二维的情况，其函数定义如式（1）～（4）所示：

Haar小波是一种正交小波，它提供了分析信号局部方面的简单且计算上有效的方法，在诸如信号和图像类的应用中是有效的;Haar小波是不连续的，不可微分，但此特性使它在很多存在突然变化的场合应用广泛[15]。因此本文使用Haar小波变换，其母小波函数如式（5）所示，尺度函数如式（6）所示。

对于上述连续的一维Haar小波函数与尺度函数，其平移与缩放按二进制离散化，如式（7）～（8）所示，展开系数hψ与hφ分别称为小波系数与尺度系数。通过对行与列的分别处理扩展到二维离散Haar小波的情况，从而构造出二维离散小波变换对应的低通滤波器[2/2 2/2]与高通滤波器[-2/2 2/2];二维离散小波逆变换的低通滤波器[2/2 2/2]与高通滤波器[2/2 -2/2]。

考虑到截取的感兴趣区最小像素尺寸接近24×24，采用一级Haar小波变换之后的子带分量像素尺寸12×12，再次分解之后感兴趣区将变得更小，并无实际意义，因此本文采取了一级小波分解。

1.3 分数阶微分

1.4 基于小波变换的分数阶微分算法

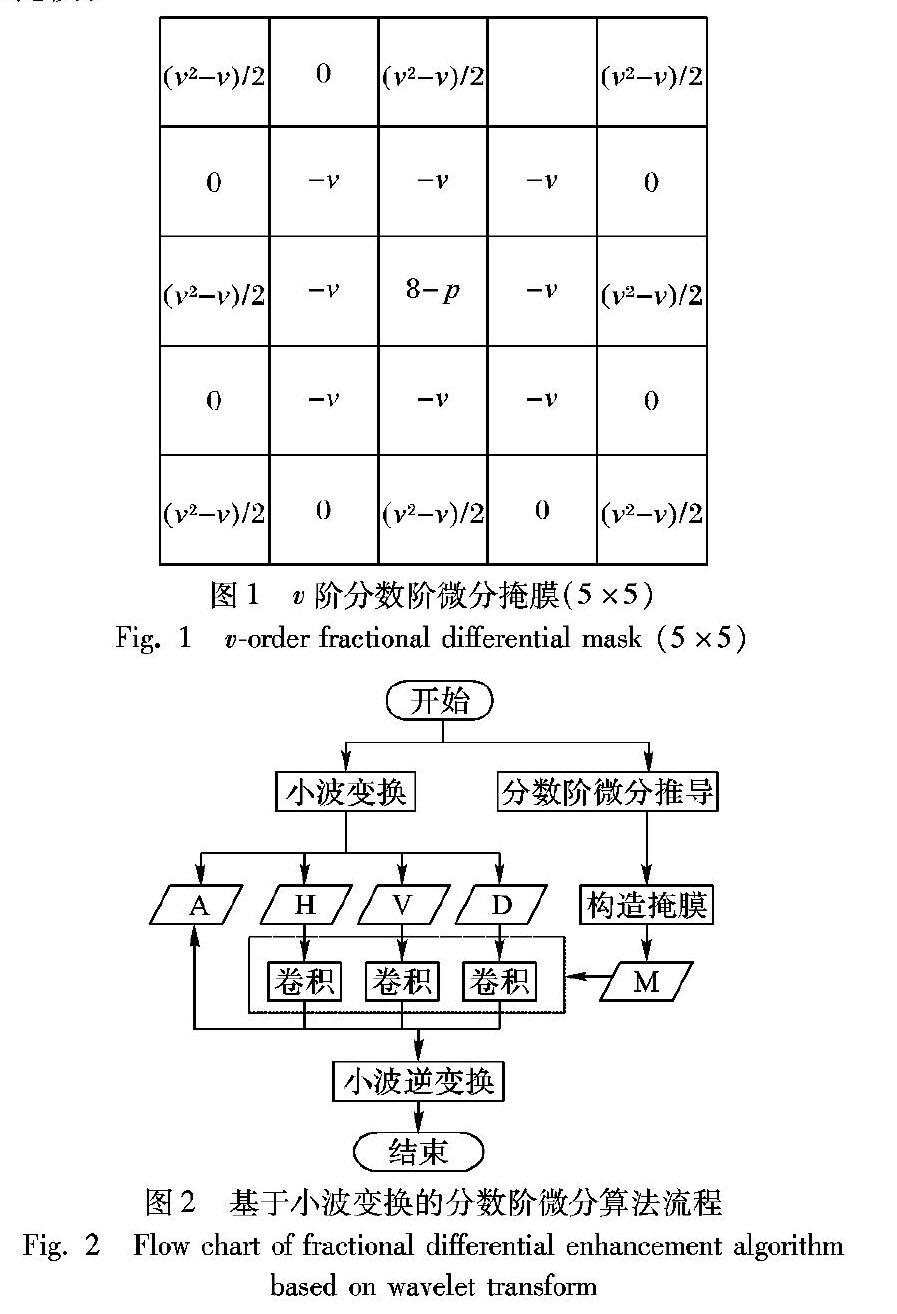
小波变换在纹理增强中的优势主要是采用多分辨率分析方法，将一幅图像分解成不同频率的分量，再对分量进行某种修正。分数阶微分的优势主要体现在它能够加强高频信息的同时，非线性保留低频信息，但对频率分辨率较为敏感。基于上述两个特点，本文根据G-L定义推导的式（11）构造了一个分数阶微分掩膜，并提出一种基于小波变换的分数阶微分算法。分数阶微分掩膜如图1所示：1）考虑8个方向的分数阶微分运算，中心点位置的值表达为1×8-p;2）中心点表达式中的数字“1”是式（11）中s（t）的系数，因为是8个方向的微分，所以为8;3）中心点表示式中p为可调节的补偿参数，在分数阶次v取尽可能大时，为了尽量不出现低频平滑细节严重丢失的情况（即不出现与整数阶微分类似的大幅地衰减灰度变化较小的纹理细节的情况），本文通过实验确定p的取值;4）掩模中的-v与（v2-v）/2分别是式（11）中s（t-1）與s（t-2）的系数;5）本文使用的数据集中，裁剪后的感兴趣区最小像素尺寸接近24×24，经过一级小波变换后子带分量大小为12×12，同时考虑到5×5邻域内能够较好地体现分数阶微分二级差分，因此本文采用窗口大小为5×5的分数阶微分掩模。

基于小波变换的分数阶微分算法流程如图2所示，主要分为如下4个主要步骤：Step1 基于二维小波变换的图像分解，图2所示只进行了一次分解，实际上应该根据待解决的问题具体情况决定分解层次（由实验效果决定）。

Step2 基于分数阶微分的定义，离散化并构造分数阶差分掩膜或称分数阶微分掩膜，即图2中的M，M的结构参考图1。

Step3 将各个高频分量别与分数阶差分掩膜进行卷积运算。本文采用一级小波分解，如果有多层分解时，应该将所有高频分量分别与分数阶差分掩膜进行卷积。

Step4 小波变换的多层分解将剩下一个近似分量，将它与Step3中的卷积后的高频分量组合到一起，进行小波逆变换，算法结束。

2 实验

对平扫CT图像进行纹理增强的研究并不多见，文献[13]中基于局部的梯度、熵、方差提出了自适应分数阶微分算法。

为了分析与比较，本文采用了7种方法对HCC与HEM的平扫图像进行纹理增强实验：Sobel、Prewitt、Laplacian、直方图均衡、文献[13]的自适应分数阶微分、本文构造的分数阶微分（图1所示），以及本文提出的基于小波变换的分数阶微分。对HCC平扫CT图像的增强结果如图3所示，图1掩膜中阶数v=0.65，补偿参数p=-0.5。对HEM平扫CT图像的增强效果与图3此类似，将肿瘤区域放大后的效果如图4所示。

主观效果评价：使用整数阶微分增强平扫的肝脏肿瘤CT图像是不合适的;直方图均衡增强了图像对比度，但严重丢失包括肿瘤区域在内的纹理细节;文献[13]的自适应分数阶微分、本文提出的分数阶微分与小波融合算法，其增强后的纹理比原图均更清晰，特别是肿瘤区域。

客观评价：信息论中数据越集中的地方熵值（也称信息熵）越小，数据越分散的地方熵值越大。图像处理中的熵是图像信息量和图像质量的一个重要评价参数，熵值越大则说明图像包含的视觉信息越丰富，图像质量也越高[13]。平均梯度与平均绝对差是度量图像清晰度的重要指标，平均梯度越大表明了图像越清晰，平均绝对差越小则表明了与原图越相近[18]。熵、平均梯度、平均绝对差的计算如式（12）～（14）所示：

本文采用1.1节所述方法对129例HCC与140例HEM图像进行预处理，然后采用前述7种纹理增强方法进行图像增强，计算原图以及增强后图像的三项性能指标：熵、平均梯度、平均绝对差。对129例HCC和140例HEM，求各性能指标的均值与方差，结果如表1所示。在表1中：u表示均值、σ表示标准差，σ仅作为样本性能指标值对性能指标均值u的偏离程度的参考。

从表1可以计算出：1）使用基于小波变换的分数阶微分算法对HCC病例的平扫CT图像进行纹理增强后，相对于原图其信息熵平均增加36.56%，其平均梯度平均增加321.56%，而平均绝对差平均增加9.287;使用文献[13]方法增强后，相对于原图其信息熵平均增加31.35%，其平均梯度平均增加198.71%，而平均绝对差平均增加6.486。

2）提出基于小波变换的分数阶微分算法对HEM病例的平扫CT图像进行纹理增强后，相对于原图，其信息熵平均增加48.77%，其平均梯度平均增加511.26%，而平均绝对差平均增加14.097;使用文献[13]方法增强后，相对于原图，其信息熵平均增加36.85%，其平均梯度平均增加230.67%，而平均绝对差平均增加4.814。

3 实验结果分析

从病理组织学与放射组学上分析，腹部CT图像中的肝脏肿瘤之间、肿瘤与正常组织之间均应该存在灰度模式的差异，但是这种差异在一些平扫CT图像中很难被清晰地观察到，传统的纹理增强方法对此类非平稳信号的图像处理难以达到预期效果，比如整数解微分、直方图均衡等。在腹部CT平扫图像中，肝脏肿瘤及其周边组织存在细微的灰度变化且其变化并不明显，即低频信息较多出现在这些区域的同时有高频信息的随机出现。从实验结果可知：1）整数阶微分虽然突出了原图边缘，即平均梯度大幅增加，但却大幅线性衰减了灰度变化较小的纹理细节（也即是低频信息），因此其总体纹理信息量反而有所减少，即熵减少;此外，平均绝对差大幅增加，即原图的信息保持量（近似分量）严重丢失。因此整数阶微分的纹理增强在医学图像的模式识别类的计算机辅助诊断中是不合适的。

2）直方图均衡对于背景和前景都太亮或太暗的图像很有用，但本文研究的CT图像显然不属于此类，因此出现变换后的图像灰度级减少、某些细节消失等现象，从图3可以直接观察到肿瘤区域的纹理丢失，这与增强后的熵值有所减少相对应;此外，直方图均衡大幅拉大了图像的对比度，因此其平均梯度大幅增加，且平均绝对差也较大，这与低频细节的纹理细节丢失相对应。

3）分数阶微分增强方法在加强图像高频信息方面表现突出，能够使图像整体特别是轮廓、边缘更加清晰，同时也能够一定程度上非线性地保留图像低频信息，即保留了平滑部分的纹理细节，因此其熵与平均梯度均有增加。然而，分数阶微分对频域分辨率较为敏感：一方面，采用较大的分数阶次增强图像时，虽高频部分得到了增强，即轮廓、边缘被突出，但是弱纹理和平滑区域基本被忽略，此时更接近于整数阶微分增强的效果，也就是低频信息部分的纹理细节会被丢失;另一方面，如采用较小的分数阶次增强图像以保留图像弱纹理和平滑区域时，图像的轮廓、边缘就会被弱化[13]。另外，如果对图像中原本是清晰、平滑的区域，也就是对含低频信息较多的区域采用分数阶微分时，虽增强了区域纹理细节，必然也会增加噪声[19]，降低了该区域的紋理稳定性，比如在小于5cm的HCC或者HEM病例的平扫CT图像中，肿瘤区域或正常肝脏区域的灰度同质性表现较强，此时同质性是一种重要的纹理特征，直接微分可能降低这种同质性。

本文提出了一种基于小波变换的分数阶微分算法：

①充分利用小波變换在局部时频分析上的优势将非平稳信号的医学图像分解成高频分量与低频分量，分数阶微分掩膜仅对高频分量进行增强，很好地避开了传统分数阶微分对频率分辨率敏感的缺陷，然后再通过小波变换的完美逆变换特性将图像重组。傅里叶变换或者轮廓波变换也是多分辨率分析中广泛使用的方法，也具有类似作用，但傅里叶变换缺乏时域处理，对非平稳信息的处理效果很不好，而轮廓波变换存在较多冗余，难以实现完美重构，改进的轮廓变换减少了冗余但同样的实现复杂。②构造了一个带补偿参数的分数阶微分掩膜对高频分量进行增强，使其能够采用较大的分数阶次并辅以一定的补偿值，在尽可能增强高频信息的同时，尽可能地保存含大量纹理细节的低频信息，并抑制了分数阶微分可能在低频部分产生的噪声。

文献[13]提出自适应分数阶微分算法，是通过分析局部的梯度、熵、方差来调整阶数以适应局部区域的频率，也是尽可能扩大高频信息并降低纹理细节的损失。

4）基于小波变换的分数阶微分，因采取了较大的分数阶次而使增强后图像的平均梯度显著增加，因此其清晰度相比原图明显增强，但与原图相似度有所减少，其对应的平均绝对差甚至比分数阶微分与文献[13]方法略都有提升，表明其对原图信息的保留略低于这两种方法，但这在基于纹理分析的医学图像计算机辅助诊断中可能是有用的（突出了有差异部分的高频细节，而对灰度变化较小的低频细节有少量丢失）。虽然分数阶微分在采用较大阶次时可能丢失更多低频细节，即熵值可能减少，但该方法由于仅对高频分量进行了增强，促使其进一步保留了近似分量的信息（低频区域的纹理细节），通过实验选择合适的阶次与补偿参数，其总体上的平均熵比分数阶微分以及文献[13]方法都较大提升。

4 结语

本文针对图像纹理增强过程中容易丢失平滑区域的纹理细节，而分数阶微分增强虽然能够非线性保留平滑区域的纹理细节，但对频率分辨率敏感的问题，提出了一种基于小波变换的分数阶微分纹理增强算法，应用于平扫CT图像的肝脏肿瘤区域的纹理增强中。实验结果表明，增强图像的肿瘤区域有更加清晰的视觉效果，且有效地保留了平滑区域的纹理细节，这对于放射科医师基于医学图像诊断是有益的;此外，增强后的肿瘤区域蕴含了更加丰富的纹理信息，对将来基于纹理分析的肝脏肿瘤计算机辅助诊断具有一定的意义。

本文也有一些局限性：首先，本研究是一个单一机构的回顾性研究，患者人群以及影像学方法存在同质性，可能存在选择性偏倚，因此难以将结果推广到其他机构;其次，本文仅采用了熵、平均梯度、平均绝对差评估了纹理信息量与图像质量，但并不全面。下一步将使用基于纹理特征的放射组学方法，检验基于小波变换的分数阶微分算法的增强研究在肝脏肿瘤的计算机辅助诊断与识别中的价值。

参考文献（References）

[1] GILLIES R J， KINAHAN P E， HRICAK H. Radiomics： images are more than pictures， they are data[J]. Radiology， 2015， 278（2）： 563-577.

[2] QIU J J， WU Y， HUI B， et al. Textural analysis of liver focal lesions with co-occurrence matrix and wavelet transform on CT： a feasible study in FNH， HEM and HCC[EB/OL]. [2018-05-10]. http：//www.dpi-proceedings.com/index.php/dtetr/article/view/6733/6325.

[3] PU Y F， ZHOU J L， YUAN X. Fractional differential mask： a fractional differential-based approach for multiscale texture enhancement[J]. IEEE Transactions on Image Processing， 2010， 19（2）： 491-511.

[4] JALAB H A， IBRAHIM R W. Texture enhancement for medical images based on fractional differential masks[J]. Discrete Dynamics in Nature and Society， 2013， 2013： 618536.

[5] HALAVAARA J， BREUER J， AYUSO C， et al. Liver tumor characterization： comparison between liver-specific gadoxetic acid disodium-enhanced MRI and biphasic CT — a multicenter trial[J]. Journal of Computer Assisted Tomography， 2006， 30（3）： 345-354.

[6] HASEBROOCK K M， SERKOVA N J. Toxicity of MRI and CT contrast agents[J]. Expert Opinion on Drug Metabolism & Toxicology， 2009， 5（4）： 403-416.

[7] YANG Y， SU Z， SUN L. Medical image enhancement algorithm based on wavelet transform[J]. Electronics Letters， 2010， 46（2）： 120-121.

[8] BHARDWAJ A， SINGH M K. A novel approach of medical image enhancement based on wavelet transform[J]. International Journal of Engineering Research and Applications， 2012， 2（3）： 2356-2360.

[9] LAVANYA C， YUGANDHAR D. Medical image enhancement based on wavelet transform[J]. IOSR Journal of Electronics and Communication Engineering， 2016， 11（1）： 20-28.

[10] PU Y， WANG W， ZHOU J， et al. Fractional differential approach to detecting textural features of digital image and its fractional differential filter implementation[J]. Science in China Series F： Information Sciences， 2008， 51（9）： 1319-1339.

[11] 张涌， 蒲亦非， 周激流. 基于分数阶微分的图像增强模板[J]. 计算机应用研究， 2012， 29（8）： 3195-3197. （ZHANG Y， PU Y F， ZHOU J L. Image enhancement masks based on fractional differential[J]. Application Research of Computers， 2012， 29（8）： 3195-3197.）

[12] LI B， XIE W. Adaptive fractional differential approach and its application to medical image enhancement[J]. Computers & Electrical Engineering， 2015， 45： 324-335.

[13] 陳向阳， 谭礼健. 基于自适应分数阶微分的医学图像增强算法[J]. 计算机应用研究， 2017， 34（12）： 3895-3898. （CHEN X Y， TAN L J. Medical image enhancement algorithm based on adaptive fractional order differentiation[J]. Application Research of Computers， 2017， 34（12）： 3895-3898.）

[14] MALLAT S G. A theory for multiresolution signal decomposition： the wavelet representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 1989， 11（7）： 674-693.

[15] DAUBECHIES I. The wavelet transform， time-frequency localization and signal analysis[J]. IEEE Transactions on Information Theory， 1990， 36（5）： 961-1005.

[16] OLDHAM K， SPANIER J. The Fractional Calculus Theory and Applications of Differentiation and Integration to Arbitrary Order[M]. Amsterdam： Elsevier， 1974.

[17] GARG V， SINGH K. An improved Grunwald-Letnikov fractional differential mask for image texture enhancement[J]. International Journal of Advanced Computer Science and Applications， 2012， 3（3）： 130-135.

[18] WANG J， LIU Z C， CHOROWSKI J， et al. Robust 3D action recognition wit random occupancy patters[C]// ECCV 2012： Proceedings of the 12th European Conference on Computer Vision， LNCS 7573. Berlin： Springer， 2012： 872-885.

[19] 吴瑞芳， 宣士斌， 荆奇. 基于局部特征的分数阶微分图像增强方法[J]. 计算机工程与应用， 2014， 50（3）： 160-164. （WU R F， XUAN S B， JING Q. Fractional differential image enhancement algorithm based on local feature[J]. Computer Engineering and Applications， 2014， 50（3）： 160-164.）