光学显微定位系统定位精度分析

陈雄 邹湘军 樊科 卢俊

摘 要：为了提高光学显微定位系统对细胞微生物识别定位的精度：一方面，必须改进手眼标定方法;另一方面，需要提高全局图像识别的准确性，因此，提出一种两步法对系统进行手眼标定。首先，通过标定固定靶标来确定系统原点，并得到视觉模块相对于系统原点的转换关系;然后，根据每次拍照的起始点位置、拍照的数量和移动的步长求解出全局图像相对于系统原点的转换关系;最后，为了进一步提高全局转换关系的准确度，提出一种基于傅里叶变换的误差矫正方法，利用傅里叶变换求解出视觉模块在移动过程中的误差，并加入系统进行补偿。实验结果表明，误差补偿之后，系统X轴方向的误差均值从10.23μm降为-0.002μm，Y轴方向的误差均值从6.9μm降为-0.50μm，显微定位系统的平均定位精度达到了99%以上。结果表明，所提方法可很好地用于光学显微定位系统对细胞微生物进行高精度的自动化抓取。

关键词：显微定位系统;手眼标定;误差矫正;傅里叶变换

中图分类号：TP391.41

文献标志码：A

文章编号：1001-9081（2019）04-1157-05

Abstract： In order to improve the accuracy of identification and localization of cell microorganisms by optical micropositioning system， on the one hand， the hand-eye calibration method should be optimized， on the other hand， the accuracy of global image recognition should be improved. Aiming at those， a two-step method for hand-eye calibration of the system was proposed. Firstly， the origin of the system was determined by calibrating the fixed target， and the transformation relationship of the vision module to the origin of the system was obtained. Then， according to the starting point position of each photograph， the number of photoing and the step size of movement， the transformation relationship of the global image to the origin of the system was solved. Finally， in order to further improve the accuracy of the global transformation relationship， an error correction method based on Fourier transform was used to obtain the error of the visual module in movement，then the error was added into the system for compensation. Experimental results show that after error compensation， the micropositioning system has the error mean value in X-axis direction reduced from 10.23μm to -0.002μm， the error mean value in Y-axis direction reduced from 6.9μm to -0.50μm， and the average positioning accuracy over 99%. The results show that the proposed method can be applied to the optical micropositioning system for high-precision automated capture of cell microorganisms.

Key words： micropositioning system; hand-eye calibration; error correction; Fourier transform

0 引言

光學显微定位系统是一种应用于细胞微生物领域的自动化识别定位系统。该系统首先通过视觉模块获得细胞微生物清晰完整的成像，并通过识别算法对目标进行视觉定位，之后，将目标图像坐标转换到自动化挑取系统（机械手）坐标，并发送给机械手进行自动化挑取，其中，图像坐标到机械手坐标的转换过程即为手眼标定[1]。由于本文所采用的光学显微定位系统制造安装精度较高，因此，忽略视觉系统的非线性问题和机械手结构的非线性问题[2]，那么，为了提高系统的精度，只能通过降低视觉模块和机械手模块之间的手眼标定误差，并对误差进行补偿[3]。

对于手眼标定国内外学者都作了大量研究。Kelly等[4]提出了一个典型的视觉机器人系统， 设计了一个定点控制器以补偿摄像机内部参数以及手眼关系转换矩阵的不确定性，并且获得了局部收敛的稳定的结果，但要求已知机器人重力项参数;田浩辰等[5]提出了一种局部线性化的像机标定算法，采用基于粗定位和精确定位两步走的算法实现了机械手的精确对位;刘苏宜等[6]提出了一种同时标定摄像机和机器人手眼的方法，该方法依据机器人手眼矩阵和机器人手爪对基坐标系位姿矩阵之间的特定关系，进行一次标定实验能同时求解出摄像机参数和机器人手眼关系矩阵;胡小平等[7]针对微装配机器人提出了一种固定视觉的手眼系统标定算法，该方法通过3个空间点在机械手基坐标系中的坐标，采用P3P（Perspective-3-Point）位姿测量原理获得相应空间点在摄像机坐标系中的坐标，建立了标定方程组，并基于最小二乘法标定出了手眼系统之间的转换矩阵;魏振忠等[8]提出了基于法兰盘的双机器人手眼标定方法，但该方法要求的机械结构相当复杂，在单机器人手眼标定时难以实现;温卓漫等[9]提出了一种基于合作靶标的在轨手眼标定方法，仅需3个特征点的图像坐标就能计算摄像机外部参数，并运用P3P方法求解位姿确保了高精度，而矩阵重排的方法使得机械臂只需要转动很小的角度，就可以完成手眼标定;张强等[10]提出了一种基于误差分布估计的加权最小二乘鲁棒估计方法，以提高机器人手眼标定的精度。以上研究者提出的方法大多针对宏观物体，精度要求均未达到微米级，且相机位置固定，而本文系统主要用于细胞微生物的识别定位，精度要求为微米级，且为了获得大视场和高清晰度的图像，相机位置需要不断地移动，因此，不能采用传统的方法对本文系统进行手眼标定。

针对以上问题，本文提出了一种两步法对系统进行手眼标定：1）标定系统原点，在系统初始状态下，相机位置不变，采用传统的固定靶标的方式对系统的原点进行标定，系统的原点设置为拍摄靶标图像时机械手所在的位置坐标;2）确定全局转换关系，根据每次拍照的起始点位置，以及拍照的数量和移动的步长确定全局转换关系。然而，根据此方法进行手眼标定，系统依然存在较大误差，而误差主要是由于视觉模块在移动过程中每次移动的距离存在误差，使得相邻的图像之间存在一定的偏移量，因此而产生了图像的全局定位误差。为了进一步提高系统的精度，本文提出了一种基于傅里叶变换的方法来矫正该误差，首先，采用傅里叶变换求解系统拍摄的相邻两张图片的实际重叠量，并与人为设定的理论重叠量进行比较，便可得到视觉模块在移动过程中的误差，之后，多次测量分别求取X和Y方向的误差均值，并将误差均值加入系统的控制单元进行补偿。实验结果表明，显微定位系统的视觉模块的误差均值明显降低，系统的整体平均定位精度达到99%以上，可以满足细胞微生物的识别定位要求。

1 显微定位系统的结构与标定原理

1.1 显微定位系统结构和组成

显微定位系统主要由视觉模块和机械手模块组成。视觉模块由相机、镜头、反射镜、闪光灯组成，相机为Andor科学级sCMOS相机Zyla5.5，晶片尺寸为16.6×14.0mm，镜头分为4倍镜、10倍镜和20倍镜，当使用10倍镜镜头时，成像精度为0.65μm/pixel。视觉模块的结构如图1所示，它共分为上下两层，以细胞培养皿为界，上面为闪光灯，下方为镜头、反射镜、相机，上下两个部分均安装在由光栅尺组成的三坐标移动平台上，由光栅尺进行联合控制运动，其中光栅尺的精度为0.2μm，在进行拍照时，上方的闪光灯与下方的相机同步运动，移动一定的步长时，闪光灯开启，相机获取图片。机械手模块的挑取装置安装在闪光灯所在的移动平台上，可由光栅尺单独进行移动控制。由于成像区域较大，无法通过一次成像获得完整的区域，因此，采用了一种如图2所示的Z字型的拍照方式对整个区域进行依次成像，最后将图像进行拼接。

1.2 显微定位系统标定原理

由于本文系统制造精度和安装精度都较高，视觉模块坐标系和机械手模块坐标系的水平度和垂直度均较好，因此，在进行系统手眼标定的过程中，忽略视觉模块坐标系和机械手模块坐标系之间的旋转变换，只考虑坐标系之间的平移变换。标定的过程分为两步：基于靶标进行系统原点的标定和进行全局区域的标定。

1.2.1 基于靶标的系统原点标定方法

描述相机成像的物理模型为小孔模型[11]。由于成像模块在拍照过程中，镜头会随着培养基表面的地貌特征而改变，因此相机的焦距在不断地改变，且相机的制造精度较高，径向畸变和切向畸变可以忽略，因此，在进行坐标转换的过程中，不能采用传统方法对相机进行标定，获取内外参数，而是直接采用相机本身的参数，每个像素点所代表的物理尺寸为pixel_um=0.65μm/pixel进行转换。转换矩阵如式（1）：

其中：img为图像坐标系;obj为靶标所在平面的坐标系;M为转换矩阵。设靶标中心点的坐标为（0，0），将视觉模块移动到靶标正上方拍摄图片，则可求出图像坐标（u， v），那么转换矩阵M便可得知。整个转换都在二维平面内进行，空间Z坐标由地貌扫描时确定。此时图像上的任意一点便可通过矩阵变换找出对应的空间坐标[12]。

机械手末端的工具坐标系Xtool与靶标坐标系Xobj之间的转换关系，如式（2），工具坐标系Xtool与机械手坐标系Xrob之间的转换关系如式（3），因为工具安装在机械手上，所以工具相对于机械手的位置不变，toolHrob为固定值，由设计安装参数便可得到。则图像坐标便可通过坐标转换变为机械手坐标系下的坐标，便于进行移动拍照时的全局定位。

Xtool到Xobj之间的转换通过固定靶标的方法进行标定得到。首先视觉模块移动到靶标上方拍摄靶标图片，计算出靶标标志点的图像坐标，并转换为Xobj坐标，之后，机械手工具末端尽可能靠近靶标中心点，得到此时的Xtool坐标，如此便可计算出Xtool到Xobj之间的转换关系objHtool。

1.2.2 全局区域标定方法

在拍摄大目标区域时，视觉模块需要按照一定的规律和步长进行移动，在不考虑坐标系之间旋转变换的情况下，机械手坐标系下的全局变换可以简化为相对于系统原点的二维平移变换，变换方式如式（4）所示：x

vimg为拼接图片中目标点的图像坐标，主要由图片所在全局图像的位置和目标点所在图片的位置确定;

图像的Z坐标由地貌扫描结果而来，由此，便可将全局的图像坐标转换为机械手下的全局三维坐标，之后，通过toolHrob转换矩阵，转换为机械手工具末端坐标，便于进行细胞微生物挑取。然而，在视觉模块移动的过程中，每次移动的步长都会有所偏差，如果直接将图像按照顺序拼接起来计算全局图像坐标u

vimg，图像的接缝处会存在较大误差，而且，误差会随着拍摄距离的增加而累积，因此，需要对视觉模块的移动误差进行矫正。

2 视觉模块移动误差测量

2.1 误差测量原理

为了验证傅里叶变换算法的准确性，本文采用了高精度的网格进行拍照拼接实验。其中整个网格的大小为4mm×4mm，每格的大小为200μm×200μm，拍摄时从左下角依次往上拍，共拍摄12张图片，分为4行3列。从中选取了左右相邻的两张图片进行拼接，其中图3（a）为直接拼接图，图3（b）为傅里叶变换拼接图，由图可知，采用傅里叶变换可以对图片进行很好的拼接，同时，可以得到相邻图片之间的实际重叠量。因此，可以采用傅里叶变换的方法进对系统的移動误差进行测量和补偿。

2.2 误差测量实验

为了进一步测量视觉模块的移动误差，本文设计了一个实验。选取高精度的微流控芯片作为拍照对象，芯片的结构尺寸为43mm×27mm，芯片内部由一些三棱柱和圆柱组成，三棱柱三角形的边长为53μm，圆柱的直径为10μm，在拍照时，采用10倍镜拍摄，成像精度为0.65μm/pixel，按照Z字形的拍照方式进行，调节相机移动的步长，使得相邻图片之间存在150μm的重叠量，共拍摄了702张图片。之后对相邻的图片进行拼接，其中图4（a）为左右拼接的效果图，图4（b）为上下拼接的效果图，由拼接算法便可得到相邻图片之间的实际重叠量，而实际重叠量与理论重叠量150μm之间的差值，便是显微定位系统视觉模块移动的误差值。

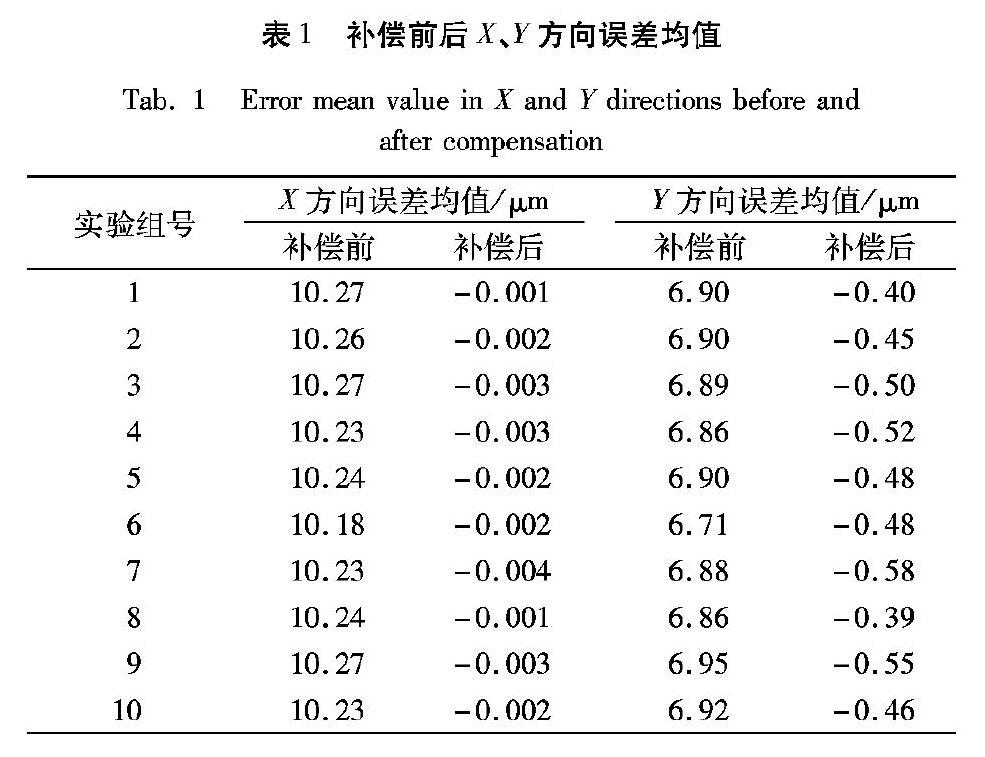
由于所拍摄的区域中有些位置特征较少，无法实现较好拼接效果，所以拍摄的702张图片并不能全部作为实验的样本，本文只选取了拼接较好的图像对作为误差实验的样本，即偏移量在阈值范围内。在计算X方向误差时，需要对左右相邻的图片进行拼接，实验中共采集了633对有效样本，其误差图如图5（a）所示，由图可知，X方向誤差值绝大部分在8～14μm区间波动，均值为10.18μm，其中存在两个较为明显的突变值，主要是由于机械结构的固有误差所造成的，因为光栅尺虽然精度较高，但是依然存在部分位置的直线度不够好，所以造成了X方向的误差突变;在计算Y方向误差时，需要对上下相邻的图片进行拼接，实验中共采集了652对有效样本，其误差图如图5（b）所示，由图可知，Y方向误差存在一个突变值，且这个突变发生在拍摄的转折点，而大部分值在4～10μm区间波动，均值为6.71μm。为保证实验数据的准确性，在相同的拍照方式下，移动微流控芯片的位置进行实验，共测试了10组不同位置的数据，X方向误差波动规律和Y方向误差波动规律均相同，其补偿前X方向和Y方向误差均值如表1所示。

3 实验与结果分析

3.1 误差补偿实验

由第2章的误差测量实验可知，X方向和Y方向误差均在一定范围内波动，且X方向的误差均值在7μm左右，Y方向的误差均值在10μm左右，且均为正数。因此，系统在进行移动拍照时，相邻图像之间X方向的实际移动距离高于理论移动距离7μm左右，而Y方向的实际移动距离高于理论移动距离10μm左右，为了降低视觉模块在移动拍照时的误差，本文采用了固定误差补偿的方式，在视觉模块进行移动拍照时，对X方向的移动步长减小7μm，对Y方向的移动步长减小10μm。为验证方法的可行性，本文采用与2.1.2节相同的拍照测量方式，补偿后的X方向误差图和Y方向误差图分别如图6所示，共拍摄了10组不同位置的样本，10组样本补偿后的X方向和Y方向的误差均值如表1所示。从表1可知：X方向的误差在进行补偿之后大多数降到了3μm以内，且误差的均值降低为0.002μm;而Y方向的误差在进行补偿之后大多数降到了5μm以内，且误差的均值降低为-0.48μm， 相对于补偿之前，误差均值有所降低。

同时，为了更加直观地展现误差补偿的效果，本文设计了另外一个实验，分别将补偿前和补偿后所拍摄的图片随机选取两张相邻的图片直接进行拼接，图7（a）、（b）分别为补偿前和补偿后所拼接的图片，由图可知，在进行误差补偿之后，相邻图像之间的拼接误差有所降低，全局图像的拼接质量有所提高。

3.2 定位精度实验

3.1节的误差补偿实验已经证明通过本文方法可以基本消除视觉模块在连续拍照过程中的误差，并且得到较为准确和完整的全局图像。同时，由于系统的精度要求较高，而机械手直径约为1mm，很难对微米级别的误差进行度量，因此为了精确验证系统的精度，本文设计了以下实验：

首先通过视觉模块进行图像采集，之后将采集的图像直接拼接起来，并求得全局图像中不同特征点的图像坐标，例如，图9（a）、（b）中A1的坐标;然后，将图像坐标按照式（4）转换为机械手下的坐标;

将该坐标输入系统，使得机械手模块与视觉模块同步移动到该点上方，之后采用视觉模块获取当前位置的图像。

重合度计算方法示意图如图8所示，A为连续图像采集时目标点所在的原始图片（如图9（a）），B为移动视觉模块所拍摄的图片（如图9（b）），利用傅里叶变换求解出重叠区域的面积A∩B。共拍摄9组不同距离的数据，重合度计算结果如表2所示。从表2可知，采用本文方法对于图像的平均定位精度达到了99%以上，可以满足细胞细胞微生物的定位要求。

4 结语

本文基于显微定位系统较高的定位精度要求，首先采用两步法对系统进行手眼标定，完成图像坐标到机械手坐标的转换;之后，针对两步法中全局转换的误差，提出了一种基于傅里叶变换的方法来提高视觉模块的移动精度，以此来进一步提高系统的定位精度。实验结果表明，显微定位系统的视觉模块的移动精度得到了有效提高，系统整体的平均定位精度达到了99%以上，基本满足细胞微生物的识别定位要求。

参考文献（References）

[1] RULAND T， PAJDLA T， KRUGER L. Globally optimal hand-eye calibration[C]// Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway， NJ： IEEE， 2012： 1035-1042.

[2] ZOU X， ZOU H， LU J. Virtual manipulator-based binocular stereo vision positioning system and errors modelling [J]. Machine Vision and Applications， 2012， 23（1）： 43-63.

[3] ZOU X， YE M， LUO C， et al. Fault-tolerant design of a limited universal fruit-picking end-effector based on vision-positioning error[J]. Applied Engineering in Agriculture， 2016， 32（1）： 5-18.

[4] KELLY R， MARQUEZ A. Robust asymptotically stable visual servoing of planar robots[J]. IEEE Transactions on Robotics and Automation， 1996， 12（5）： 759-766.

[5] 田浩辰， 张银龙， 赵海文， 等.机械手视觉系统的非均匀标定法研究[J]. 制造业自动化， 2016， 38（5）： 41-47. （TIAN H C， ZHANG Y L， ZHAO Y W， et al. Non-uniform calibration method research of loading manipulator system based on vision positioning[J]. Manufacturing Automation， 2016， 38（5）： 41-47.）

[6] 刘苏宜， 王国荣， 石永华.激光视觉机器人焊接中摄像机和手眼的同时标定[J]. 华南理工大学学报（自然科学版）， 2008， 36（2）： 74-77， 82. （LIU S Y， WANG G R， SHI Y H. Simultaneous calibration of camera and hand-eye in robot welding with laser vision[J]. Journal of South China University of Technology （Natural Science Edition）， 2008， 36（2）： 74-77， 82.）

[7] 胡小平， 左富勇， 謝珂.微装配机器人手眼标定方法研究[J]. 仪器仪表学报， 2012， 33（7）： 1521-1526. （HU X P， ZUO F Y， XIE K. Research on hand-eye calibration method for micro-assembly robot[J]. Chinese Journal of Scientific Instrument， 2012， 33（7）： 1521-1526.）

[8] 魏振忠， 张博， 张广军.双机器人系统的快速手眼标定方法[J]. 光学精密工程， 2011， 19（8）： 1895-1902. （WEI Z Z， ZHANG B， ZHANG G J. Rapid hand-eye calibration of dual robot system[J]. Optics and Precision Engineering， 2011， 19（8）： 1895-1902.）

[9] 温卓漫， 王延杰， 邸男， 等.基于合作靶标的在轨手眼标定[J]. 仪器仪表学报， 2014， 35（5）： 1005-1012. （WEN Z M， WANG Y J， DI N， et al. On-orbit hand-eye calibration using cooperative target[J]. Chinese Journal of Scientific Instrument， 2014， 35（5）： 1005-1012.）

[10] 张强， 曲道奎， 徐方， 等.基于误差分布估计的机器人手眼标定方法研究[J]. 计算机测量与控制， 2018， 26（4）： 246-249. （ZHANG Q， QU D K， XU F， et al. Error distribution estimation based robot hand-eye calibration[J]. Computer Measurement & Control， 2018， 26（4）： 246-249.）

[11] ZHANG Z. A flexible new technique for camera calibration[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2000， 22（11）： 1330-1334.

[12] 叶溯， 叶玉堂， 刘娟秀， 等.补强片自动贴片系统高精度手眼标定方法[J]. 应用光学， 2015， 36（1）： 71-76. （YE S， YE Y T， LIU J X， et al. High-precision hand-eye calibration method for automatic stiffness bonder[J]. Journal of Applied Optics， 2015， 36（1）： 71-76.）

[13] 郭永刚， 葛庆平， 姜长胜.基于傅里叶变换的红外热波图像拼接[J]. 计算机应用研究， 2007， 24（1）： 227-228. （GUO Y G， GE Q P， JIANG C S. FFT-based image mosaicing of infrared thermal wave images [J]. Application Research of Computers， 2007， 24（1）： 227-228.）