幼虫期气象因子对马尾松毛虫影响及在预测预报中的应用

摘要：通过潜山市数据实证分析表明，马尾松毛虫的发生与1～2龄幼虫气温、降雨不具有线性相关性，但具有较高的非线性相关性。利用其非线性相关性，采用神经网络建模，对潜山市2015年～2018年发生数据进行验证，预测精度均大于90%。

关键词：马尾松毛虫;幼虫期;气温;降雨;神经网络;非线性

中图分类号： S763.421                                  文献标识码：  A                    DOI編号：   10.14025/j.cnki.jlny.2019.14.061

马尾松毛虫（Dendrolimus punctatus Walker）是潜山市的主要历史性森林害虫，呈周期性发生。大发生年份，除了对松林造成严重危害之外，还严重威胁人畜健康，诱发松毛虫病。

1 数据来源与建模工具选择

马尾松毛虫发生防治面积数据来源于安徽省潜山市1983年～2014年监测数据，气象数据来源于国家气象信息中心《中国地面国际交换站气候资料日值数据》，如表1所示。

建模工具选择MathWorks公司的MATLAB R2016年。由于潜山市属于2～3代马尾松毛虫发生区，以幼虫越冬，越冬代即为上一年的第二代，为了便于建模分析，对潜山市马尾松毛虫监测数据进行适当变换，将第二代发生面积与翌年越冬代发生面积合并，气象数据也作相应的合并，如表1。

2 线性相关性分析

基于余燕等学者研究，马尾松毛虫的发生与1～2龄幼虫气温、降雨有较高的相关性。选取第1、第2龄极低气温（℃），第1、第2龄平均气温（℃），第1、第2龄积温（日度），第1、第2龄降雨量（mm）作为分析建模气象因子，如表1。对表1数据进行线性相关性分析，如表2所示。从表2可以看出，马尾松毛虫发生面积与第1、第2龄极低气温（℃），第1、第2龄平均气温（℃），第1、第2龄积温（日度），第1、第2龄降雨量（mm）存在一定的相关性，但线性相关性不明显。

3 非线性相关性分析

采用神经网络建模，对表2数据进行分析，神经网络建模参数为：

% Map Minimum and Maximum Input Processing Function

function y = mapminmax_apply（x，settings）

y = bsxfun（@minus，x，settings.xoffset）;

y = bsxfun（@times，y，settings.gain）;

y = bsxfun（@plus，y，settings.ymin）;

end

% Sigmoid Symmetric Transfer Function

function a = tansig_apply（n，～）

a = 2 ./ （1 + exp（-2*n）） - 1;

end

% Map Minimum and Maximum Output Reverse-Processing         Function

function x = mapminmax_reverse（y，settings）

x = bsxfun（@minus，y，settings.ymin）;

x = bsxfun（@rdivide，x，settings.gain）;

x = bsxfun（@plus，x，settings.xoffset）

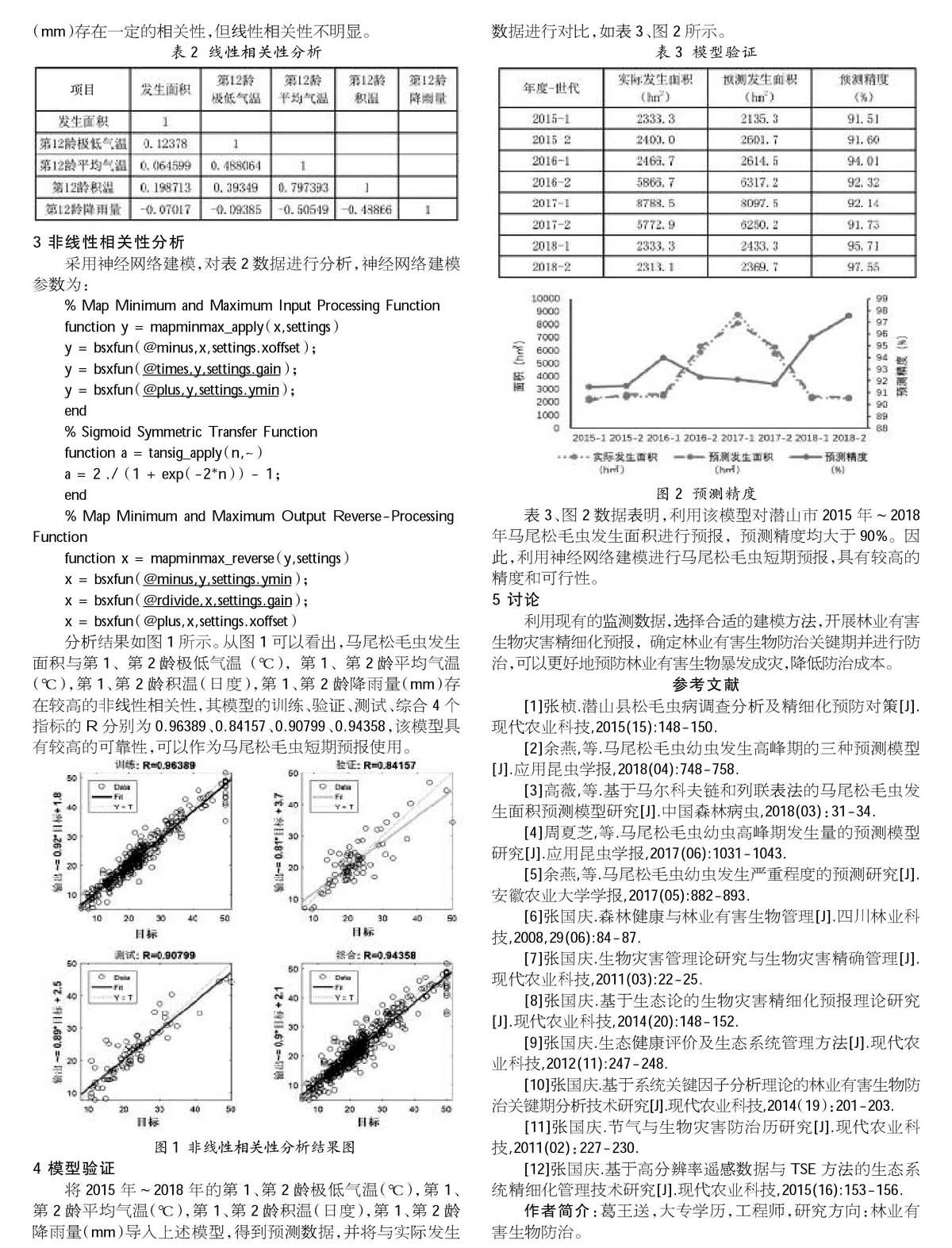
分析结果如图1所示。从图1可以看出，马尾松毛虫发生面积与第1、第2龄极低气温（℃），第1、第2龄平均气温（℃），第1、第2龄积温（日度），第1、第2龄降雨量（mm）存在较高的非线性相关性，其模型的训练、验证、测试、综合4个指标的R分别为0.96389、0.84157、0.90799、0.94358，该模型具有较高的可靠性，可以作为马尾松毛虫短期预报使用。

4 模型验证

将2015年～2018年的第1、第2龄极低气温（℃），第1、第2龄平均气温（℃），第1、第2龄积温（日度），第1、第2龄降雨量（mm）导入上述模型，得到预测数据，并将与实际发生数据进行对比，如表3、图2所示。

表3、图2数据表明，利用该模型对潜山市2015年～2018年马尾松毛虫发生面积进行预报，预测精度均大于90%。因此，利用神经网络建模进行马尾松毛虫短期预报，具有较高的精度和可行性。

5 讨论

利用现有的监测数据，选择合适的建模方法，开展林业有害生物灾害精细化预报，确定林业有害生物防治关键期并进行防治，可以更好地预防林业有害生物暴发成灾，降低防治成本。

参考文献

[1]张桢.潜山县松毛虫病调查分析及精细化预防对策[J].现代农业科技，2015（15）：148-150.

[2]余燕，等.马尾松毛虫幼虫发生高峰期的三种预测模型[J].应用昆虫学报，2018（04）：748-758.

[3]高薇，等.基于马尔科夫链和列联表法的马尾松毛虫发生面积预测模型研究[J].中国森林病虫，2018（03）：31-34.

[4]周夏芝，等.马尾松毛虫幼虫高峰期发生量的预测模型研究[J].应用昆虫学报，2017（06）：1031-1043.

[5]余燕，等.马尾松毛虫幼虫发生严重程度的预测研究[J].安徽农业大学学报，2017（05）：882-893.

[6]张国庆.森林健康与林业有害生物管理[J].四川林业科技，2008，29（06）：84-87.

[7]张国庆.生物灾害管理论研究与生物灾害精确管理[J].现代农业科技，2011（03）：22-25.

[8]张国庆.基于生态论的生物灾害精细化预报理论研究[J].现代农业科技，2014（20）：148-152.

[9]张国庆.生态健康评价及生态系统管理方法[J].现代农业科技，2012（11）：247-248.

[10]张国庆.基于系统关键因子分析理论的林业有害生物防治关键期分析技术研究[J].现代农业科技，2014（19）：201-203.

[11]张国庆.节气与生物灾害防治历研究[J].现代农业科技，2011（02）：227-230.

[12]张国庆.基于高分辨率遥感数据与TSE方法的生态系统精细化管理技术研究[J].现代农业科技，2015（16）：153-156.

作者简介：葛王送，大专学历，工程师，研究方向：林业有害生物防治。