动量轮微振动机理及仿真

马艳红，刘珊珊，王虹，洪杰，*

（1.北京航空航天大学 能源与动力工程学院，北京100083； 2.先进航空发动机协同创新中心，北京100083；3.北京控制工程研究所 精密转动和传动机构长寿命技术北京市重点实验室，北京100094）

动量轮作为卫星等航天器的重要定位、储能、控制等功用的转动部件，在轨高速旋转工作时由于结构系统的几何尺寸和力学特征的微小变化会引起多种振动激励，使振动输出载荷中包含宽频微幅振动，从而诱发卫星系统低振动能量级的扰动（即微振动），虽然对航天器结构不会产生明显损伤，但会严重影响卫星上高精度仪器的分辨率，限制卫星指向精度和姿态稳定度性能的不断提高[1]，是影响高性能航天器指向精度和成像质量的重要指标。

微振动的表现特征为幅值小（0.01g量级）、频率成分丰富（多倍频）、频带宽（1～1 000 Hz）、存在行波振动。近年来，航天器平台对指向精度和姿态稳定度要求不断提升，指向精度要求达到0.01°，甚至角秒级，姿态稳定度达到10-3～10-4（°）/s，甚至10-5（°）/s量级。因此，动量轮的微振动问题愈发凸显，严重制约了中国新研高精度卫星的发展。

国内外关于动量轮微振动机理的相关研究始于20世纪70年代，主要包括2个方面。一种是基于试验结果反向建立的动量轮扰动模型。Hasha[2]将扰动拟合为一系列与动量轮转速平方成正比的离散谐振，根据试验结果确定经验模型的系数，但由于未考虑惯性力矩对转子结构的作用以及轴承扰振作用，使得部分高阶的谐波响应明显低于试验结果。Masterson[3]基于此模型，推导动量轮不平衡量与扰动的关系，并采用弹簧-阻尼线性模型，建立了基频谐振解析模型，但无法解释响应中出现反进动的原因。Liu等[4]将宽频噪声引入扰动，根据试验不断校正，才较好地解释了动量轮低速运转时振动模态及正反进动现象，但对于动量轮系统本身的激励原理尚不清晰，导致高频、高阶的响应现象无法解释。另一种是基于激励种类正向建立的转子动力学方程。Kim[5]研究了冷热交变等外部激励对动量轮的扰动作用，但忽略了内部的旋转激励，缺乏试验数据支撑。周伟勇[6]基于线性假设建立了动量轮振动方程，仅考虑了轮体的静不平衡量，并未将动不平衡、陀螺效应及轴承碾压作用等因素引入方程中进行微振动性能预测，只获得了基频谐波的振动幅值。李连军和戴金海[7]提出转子系统内部存在摩擦、弹性振动及质量分布不均等激励作用，但仍采用Jeffcott转子模型理论推导并建立相关仿真模型分析时域内的振动响应，未能很好地与试验相吻合。罗睿智等[8]分析了轴承滚动面几何误差的非线性接触引起的预紧力波动，据此得到的数值解与高阶振动瀑布图符合得很好，但缺少动量轮自身结构特征引起激励的机理分析。可见，由于微振动振源及激励模式的不清楚导致始终未能建立精细的动量轮振动模型与试验相互对照。

综上可知，现有研究多将动量轮结构系统看作简化对称的稳定结构，研究不平衡量等激励作用下转子的振动响应，较少关注动量轮在工作过程中自身结构特征的微小变化及其引起的激励作用。而这些正是动量轮扰振机理研究的核心问题，不能忽略或简化，综合考虑这些影响因素才能有针对性地开展动量轮微振动抑制技术研究。本文建立动量轮结构系统动力学模型，考虑支承不对称的影响，重点研究动量轮几何构形的非均匀性引起的微变形、轮缘的局部微振动导致的结构参数激励、支点动载荷形成的基频激励和轴承碾压形成的高频载荷激励，并通过仿真和试验结合进行验证。

1 旋转态动量轮扰振机理分析

动量轮的结构系统示意图如图1所示。不考虑电机等驱动装置，动量轮结构系统包括轮体结构、轴承支承结构、支杆结构与壳体安装座结构四大部分。轮体结构本身为轮缘-轮辐的形式，在几何构形上具有突变的结构特征，使轮体结构质量/刚度分布具有非均匀性。轴承支承结构为外环旋转、内环固定的两对角接触球轴承，经过轴承滚子顺序碾压作用，将振动能量以高次谐波传递给支杆结构。支杆结构通过单端悬臂支承方式固定在壳体安装座结构上，并通过安装座与卫星星体相连。

为了分析动量轮结构系统在高速状态下的扰振源，利用达朗贝尔原理可以得到多自由度、有阻尼系统的动力学方程为

式中：q为广义坐标；M 为质量矩阵；C为阻尼矩阵；K为刚度矩阵；Q为系统广义外力。

对于一般的机械振动系统，主要是研究广义外力Q的变化引起的振动响应变化。在无外部激励的情况下，广义外力主要来自不平衡量。对于动量轮结构系统，虽经过精密的高转速动平衡，但在工作时依然存在微振动。这就说明除了不平衡量的影响外，还存在其他的影响因素，即本文关心的重点为：一方面质量、阻尼和刚度这3个矩阵都是与动量轮自身结构特征有关的参数，在旋转作用下发生的微小变化都会作为激励，其中质量矩阵M 的变化主要来源于转动惯量Ji各项；另一方面Q包括系统惯性载荷引起的支点动载荷及轴承碾压作用下的高频谐波激励。

建立动量轮结构系统动力学模型如图2所示。将动量轮结构简化为轮缘-轮辐形式的轮体，轴承简化为2对径向刚度不同的线性弹簧单元，计及其阻尼作用。考虑到支杆结构由于单端悬臂支承方式引起的质量/刚度不对称，利用有限元素法将结构系统离散成3个子域（即支杆段1、轮体段和支杆段2），图2中每2个标记节点间为同一子域。

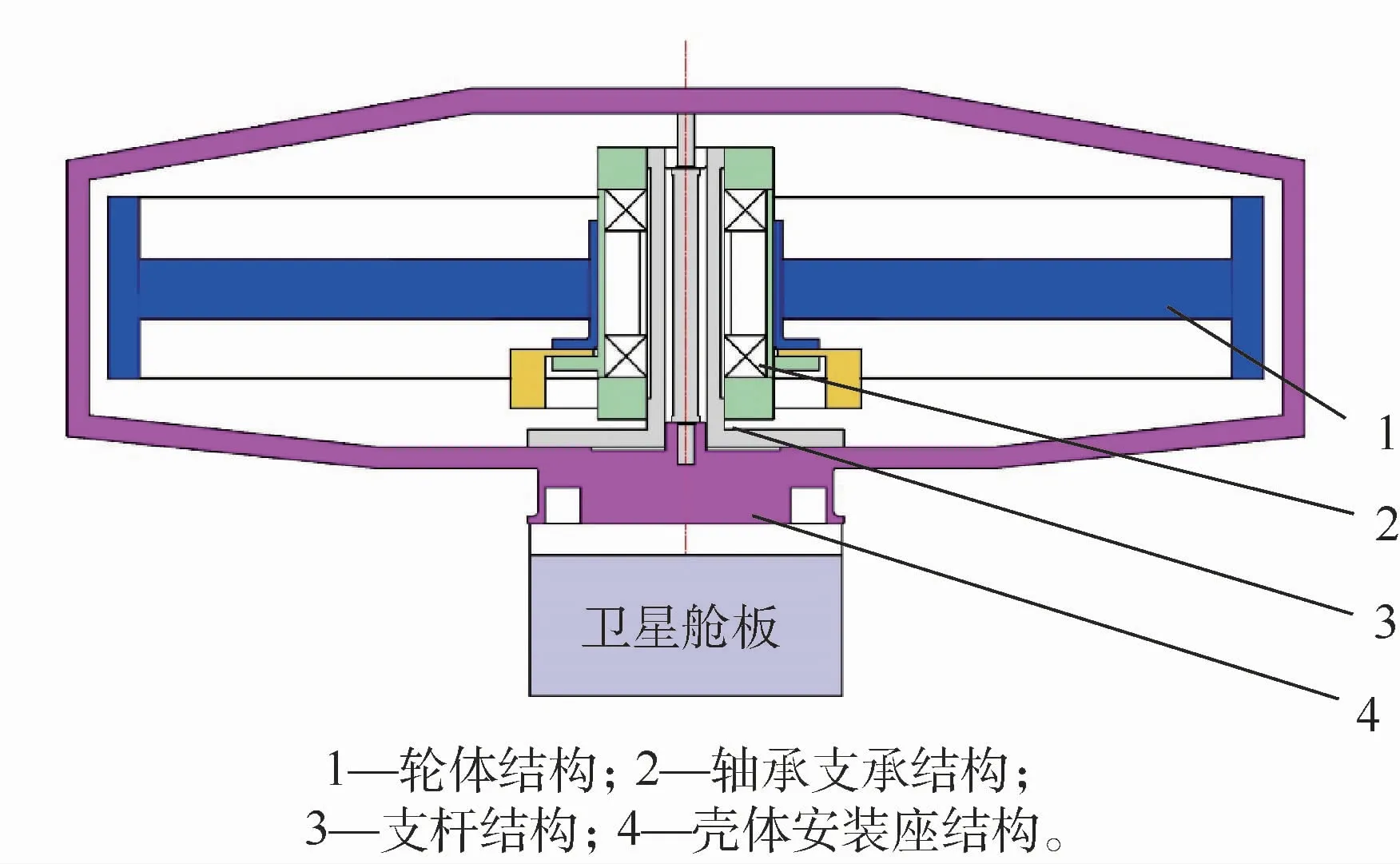
图1 动量轮结构系统示意图Fig.1 Structural system schematic diagram of momentum wheel

图2 动量轮结构系统动力学模型Fig.2 Structural system dynamic model of momentum wheel

根据精度各子域内部可取有限多个节点。系统广义坐标q表示各节点的5个自由度：位移x、y、z和转角 θx、θy。

式（1）中的质量矩阵M 的表达式为

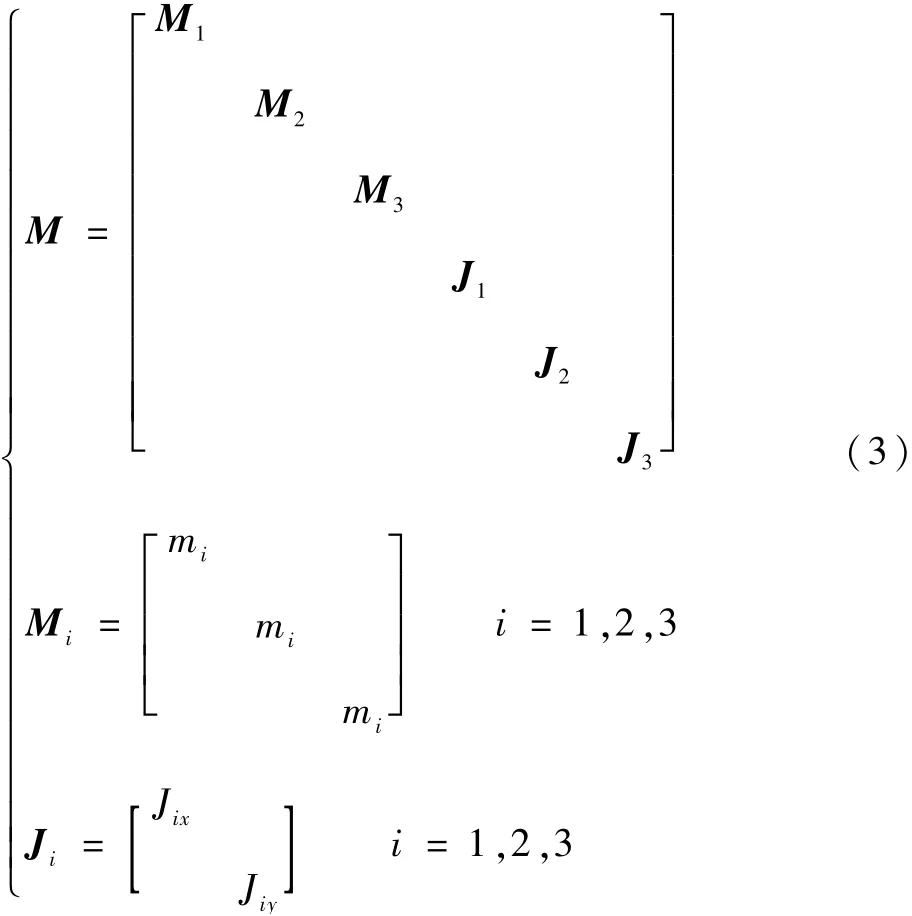
式中：Mi为第i个子域的平动质量矩阵；Ji为转动惯量矩阵；mi为第i个子域的结构质量；Jix和Jiy分别为结构绕x轴和y轴的直径转动惯量；J2为轮体结构的转动惯量矩阵，在高速旋转状态下其微小扰动构成了参数激励的主要部分。

1.1 轮体结构的参数激励

轮体结构144°剖视图如图3所示，其几何特征为采用大直径轮缘-轮辐组合结构，通过底部安装边与轴承支承结构连接，力学特征表现为转动惯量大，但轮辐质量及其对轮缘的约束刚度沿周向具有非均匀性，在高速旋转状态下的局部振动作用下，会造成转动惯量的非均匀性和分散性，进而作为参数激励，引起系统的微振动。

图3 轮体结构144°剖视图Fig.3 144°section view of wheel body structure

1.1.1 质量分布非均匀的影响

转动惯量是转动体绕转轴旋转时质量惯性的量度，包括直径转动惯量Jx、Jy和极转动惯量Jz。由于轮体几何结构非均匀，导致质量的非均匀分布，如图4所示，用简化二维截面计算轮缘-轮辐的直径转动惯量。选取与轮体底部安装边中心固连直角坐标系Oxyz，设第1条轮辐与x轴的夹角为θ1。则转动惯量表达式为

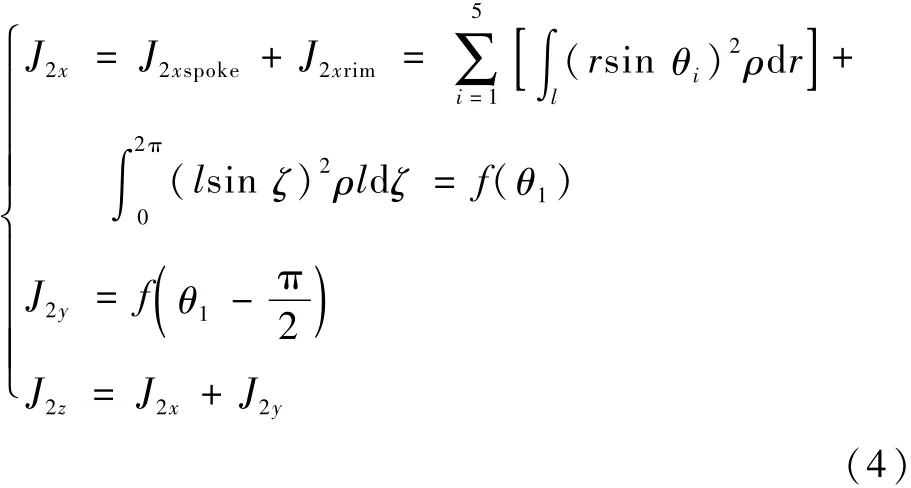
式中：l为轮缘半径；ρ为材料密度；θi分别代表5条轮辐与x轴的夹角；r为轮辐微元体所在半径长度；ζ为轮缘微元体与x轴的夹角。

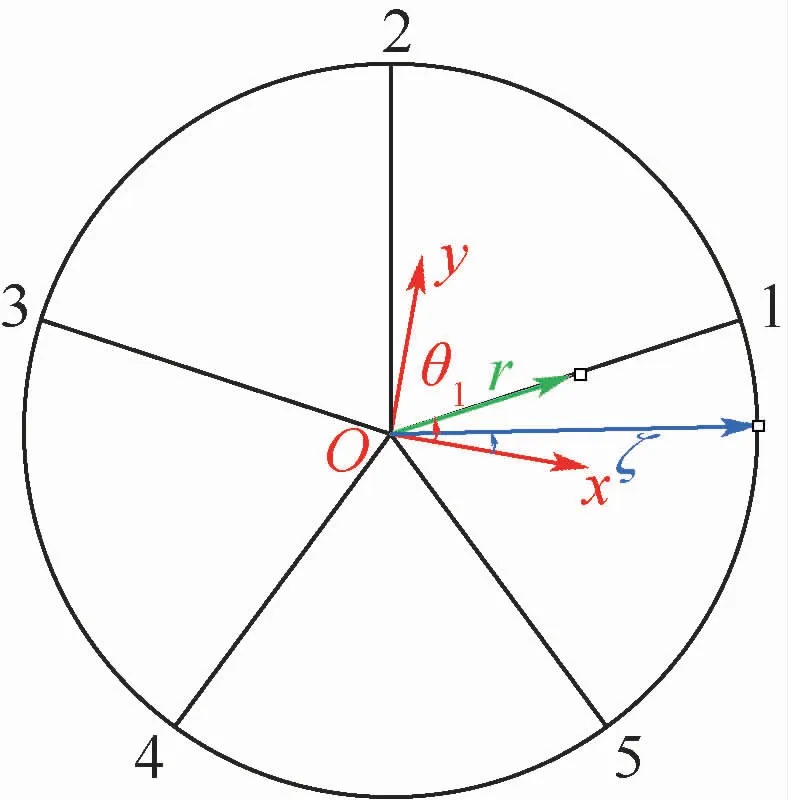
图4 转动惯量计算图Fig.4 Moment of inertia calculation diagram

化简式（4），得到

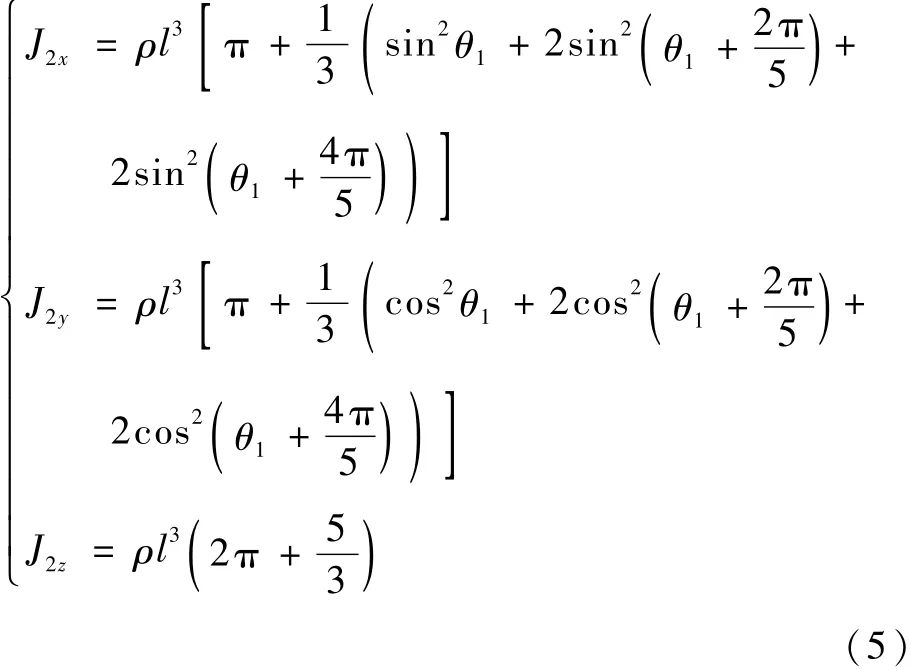
可见，J2x和J2y是 θ1的函数，而J2z与 θ1无关，是一定值，只有当存在不平衡量时会发生变化。对J2x求导（J2y等价），得到

根据式（6），J2x的周期是 π，且当时，J2x取极值。此时的x轴和y轴即为惯性主轴。绘制无量纲J2x随 θ1（0～360°）变化的关系，如图5所示。随角度的不同，任意时刻的直径转动惯量呈周期性变化，即质量矩阵M 一项中的J2x和J2y项在工作过程中具有非均匀性。

图5 无量纲直径转动惯量J2x分布Fig.5 Dimensionless diameter moment of inertia J distribution

1.1.2 刚度分布非均匀的影响

高速旋转状态下，轮缘和轮辐的主要受力形式是离心拉应力，而刚度是抵抗变形的能力，由于二者沿径向所受的拉力和刚度不同，使其变形不协调，相互约束。这种非均匀的微变形会使转动惯量发生微变化。

轮辐各微元体所受离心拉应力大小与直径成正比；轮缘厚度小、半径近似为一定值，微元体所受离心力也为一定值。就刚度而言，以轮缘为研究对象，逐渐靠近轮辐连接处的约束刚度逐渐增大，而从轮缘微元体逐渐远离轮辐的旋转过程中，刚度逐渐减小。以轮缘微元体与轮辐中心线夹角为自变量建立极坐标系，如图6所示。绘制轮缘无量纲径向刚度的变化示意图，如图7所示。可见，径向刚度呈周期性变化，周期为0.4π（约72°），在 θ=0.2 kπ处取极大值。

轮体旋转状态变形放大示意图如图8所示，线条对应转速为零时的状态，轮辐变形程度与直径成正比，而轮缘的径向变形由于受轮辐连接刚度的限制，使得沿周向观察时的变形程度非均匀，这种变形状态下的转动惯量J2x会存在微小扰动 ΔJ2x，是与转速有关的函数，即 ΔJ2x（Ω）。

图6 轮缘径向刚度极坐标系示意图Fig.6 Schematic diagram of rim radial stiffness in polar coordinate system

图7 轮缘无量纲径向刚度Kθ分布Fig.7 Dimensionless radial stiffness Kθof rim distribution

图8 轮体旋转状态变形放大示意图Fig.8 Schematic diagram of amplified deformation of wheel body under rotation

1.1.3 轮缘行波振动的影响

轮缘的结构形式为壳体，在旋转状态下存在局部振动，其振动示意图如图9所示，主要呈现出“花瓣形”的径向变形。转动轮盘局部振动的位移主要为轴向，即与转动轴矢量方向一致，基本只有离心力的作用。而转动壳体微元素变形如图10所示，主要为径向变形u，由于变形速度矢量与转动速度矢量w存在夹角，二者会形成科里奥利力。也就是说，轮缘在旋转状态不仅受离心力的作用使得刚度增加，同时在科里奥利力的作用下对于径向位移为正和负的微元体分别产生刚度增加或减小的影响，进而影响转动惯量。而这种非确定的微小变化频率与前后行波的频率ω相同，即 ΔJ2x（ω）。

图9 轮缘振动示意图Fig.9 Schematic diagram of vibration of rim

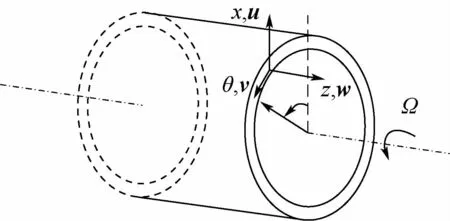
图10 转动壳体微元素变形Fig.10 Microelement deformation of rotating shell

图11 轮缘共振示意图Fig.11 Schematic diagram of resonance of rim

轮缘共振示意图如图11所示。在科里奥利力的影响下，轮缘的前后行波频率在与转动轮体固连的动坐标系中不同，在静坐标系中的频率为

式中：ωd为轮缘转动的固有频率。

只有当周向波数m=1时，前后行波频率相同；当m＞1时，前后行波频率不同[9]，表现在共振图上的“V”型线。当激振力频率与正或反进动频率相等时都会产生较大响应[10]。

综上，考虑到轮体结构本身的几何（质量）非均匀性，转动惯量在旋转状态下是与角度有关的确定性函数，但由于刚度分布非均匀引起的离心载荷下微变形及轮缘的局部微振动都会使得直径转动惯量具有非确定性，其表达式为

式中：J2x和J2y等价，等式右边J2x（θ）表示与角度的关系，ΔJ2x（Ω）表示与转速相关的扰动，ΔJ2x（ω）表示与行波振动频率相关的扰动。

因此，直径转动惯量旋转状态下会在一区间内扰动，如图12所示，仍以角度为自变量，转动惯量在每一点都具有带宽，成为系统的参数激励。

1.2 动量轮结构系统的载荷激励

动量轮高速旋转时会将残余不平衡量放大，引起与转速成平方关系的振动响应，这种不平衡激励是最基本的也是不可避免的，然而在平衡精度已经很高的基础上，结构系统依然存在相对较大的振动，一方面是因为转子的弹性变形引起的惯性力矩，通过支点将转子振动的能量转化为动载荷；另一方面轴承传播振动能量过程中，本身作为激励源又会引起复杂的高倍频激励载荷。

图12 J2x区间扰动示意图Fig.12 Schematic diagram of interval disturbance of J2x

1.2.1 支点动载荷

动量轮结构系统旋转状态的变形包括离心载荷产生的静变形及振动变形。静变形是多种固有模态振型的叠加。整体模态振型主要有3种形式，如图13所示，分别是径向平移、径向摇摆及轴向平移[11]。与Jeffcott转子不同，单端悬臂支承的动量轮结构系统中，轮体两侧轴承的刚度不完全相同，内部支杆更容易在轮体旋转作用下发生弯曲变形。

当轮体发生径向摇摆、高频弯曲振动变形或者由于结构特征非均匀引起径向变形不对称时，都会使得轮体公转轴和自转轴产生夹角，从而产生惯性力矩MG。也就是说，作用在支点上的总力矩Mg=不平衡力矩Mz+惯性力矩MG。支点动载荷示意图如图14所示。

Mz是由于轮体偏摆产生的不平衡量引起的力矩，其表达式为

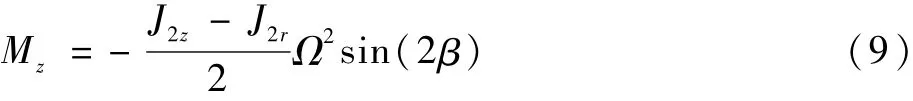
式中：β为轴心线偏离的程度；J2z为轮体的极转动惯量；J2r为轮体的平均直径转动惯量。

惯性力矩MG的表达式为

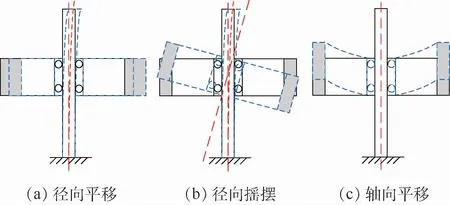
图13 动量轮整体模态振型示意图Fig.13 Schematic diagram of modal shape of overall momentum wheel

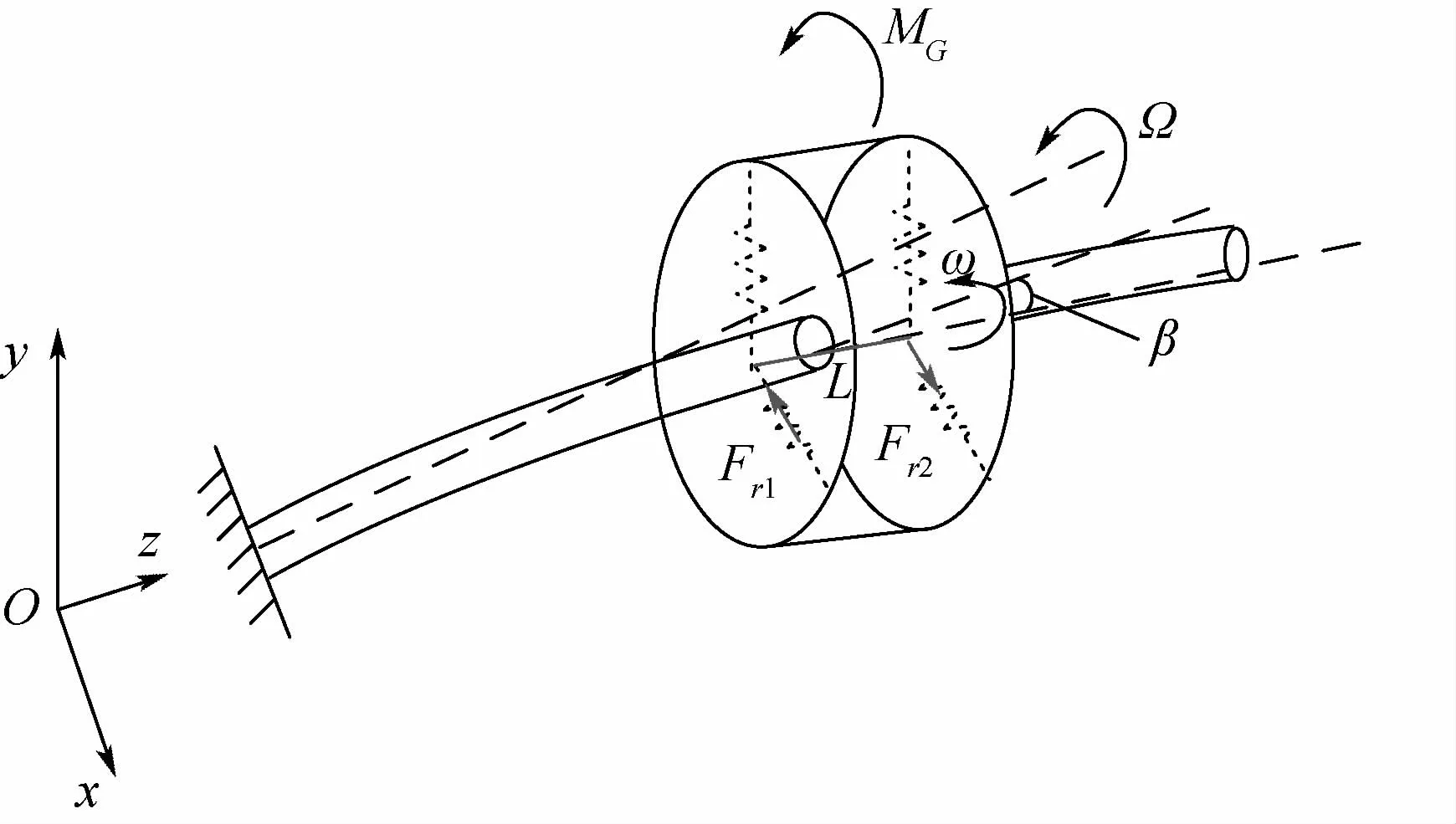
图14 支点动载荷示意图Fig.14 Schematic diagram of dynamic load on fulcrum

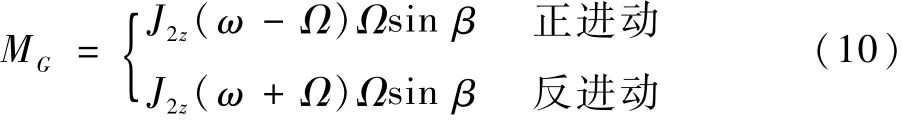
由此可得，当 β很小时，支点所受总力矩大小为

而支点动载荷需满足如下关系式：

式中：L为支点间距；Fr1为1#轴承外环上作用的径向载荷；Fr2为2#轴承外环上作用的径向载荷。

由式（12）可见，支点动载荷与转速成函数关系，协调进动时支点总力矩的大小与转速的平方成正比，此时支点动载荷也与转速平方成正比。实际上，不仅是轮体弯曲时会产生支点动载荷，即使轮体和支杆的变形程度都很小，只要支杆有弯曲（或弯曲的趋势）时（见图13（a）、（b）），都会存在支点动载荷，其大小与转速和弯曲变形的程度有关[12]。

1.2.2 轴承滚子碾压激励

支点动载荷会通过轴承组件将轮体的振动能量传递给支杆结构和壳体安装座结构，进而传递到卫星上。若支点动载荷很小，经过轴承有可能会衰减，但若支点动载荷很大，就会在支杆上产生较大的振动响应。轴承组件包括球形滚子、内外环及保持架等，由于非连续的结构特征会成为新的振源，产生高倍频激励。这种激励的频率成分非常丰富，且分布范围很宽。

高频激励产生的主要原因是轴承内部滚子上载荷的分布具有周期性变化规律，会形成与受力滚子数有关的高倍频激励。此外，滚动面上的微小几何误差会产生与轴承各部件固有频率相关的高倍频激励[13]。

轴承结构示意图如图15所示。其各项结构参数决定了零件之间相对的旋转关系，进一步确定了轴承的特征频率。设动量轮的转速为Ω，则轴承外环转速为 Ω，内环转速为0。据此可以分别计算出保持架的转速及滚动体自转转速[14]。

根据保持架的线速度为内外滚道线速度的平均值，可得保持架转速为

根据滚动体与外环接触点线速度相同，可得滚动体自转转速为

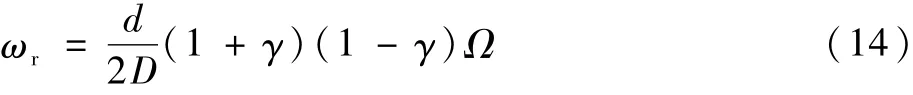
设滚子数为p，轴承转动频率为f=Ω/（2π），则轴承的特征频率如表1所示。

轴承在滚动碾压过程中会存在上述各种特征频率成分的激励及谐波叠加形成的频率，这是轴承固有的特点，下面分析载荷作用引起的行波激励。

假设滚动体与滚道为点接触，按照Hertz接触弹性理论，可知滚动体与滚道接触点的法向载荷-位移关系式为

式中：Q为滚动体与滚道接触点的法向载荷；δ为滚动体与滚道接触点的位移；k为与两接触体材料参数和接触点曲率半径都有关的系数[15]。

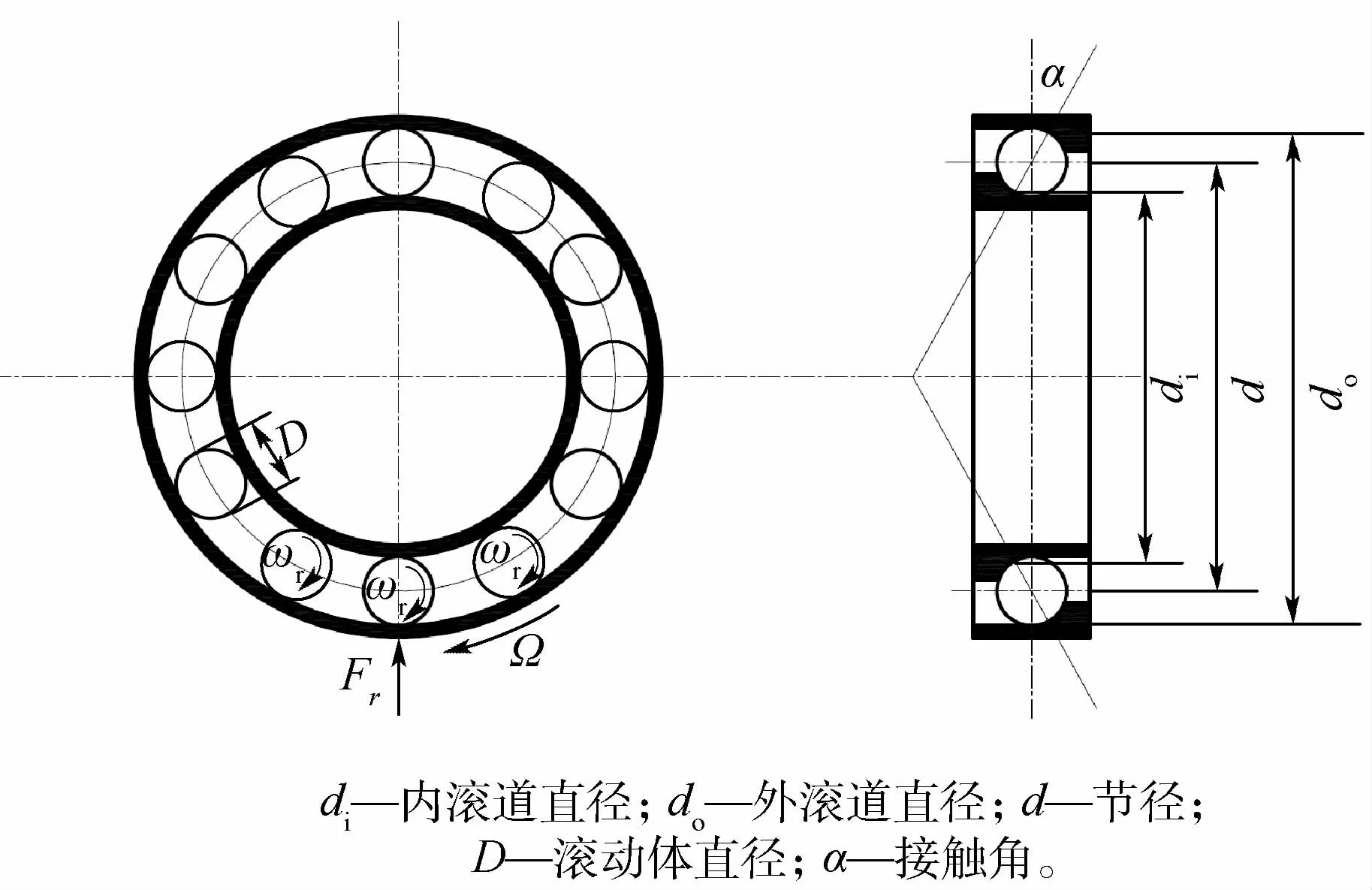
图15 轴承结构示意图Fig.15 Schematic diagram of bearing structure

表1 轴承特征频率Table 1 Bearing characteristic frequency

轮体的振动作用在轴承外环上，表现为径向（法向）载荷和轴向载荷的形式，再经滚动体传递到内环。对于几何形状理想的轴承，其轴向载荷可以认为由全部滚动体共同承担，而径向载荷由扇区内滚动体承担。

图16为径向载荷作用下的滚动体变形。滚动体与轴心连线相对载荷作用线的夹角为φ时的径向位移为

式中：δr为φ=0时对应的滚道径向移动量，此时有 δφ=0=δmax。

式（16）可化为如下比例形式：

结合式（15）和式（17），得

式中：Qφ为夹角为φ时滚动体与滚道接触点法向载荷；Qmax为最大接触载荷。

利用力的平衡，受力扇区内滚子上全部载荷在竖直方向的分量应等于轴承外环上作用的径向载荷，即

式中：Φ为最大受力扇区半角。

当径向载荷Fr确定时，可以求出δr，进而可以解得Qφ的分布。受载区的每颗滚动体都受由小变大再变小的周期性载荷。动量轮振动时会产生频率等于转频的多个相位和幅值都不同的径向载荷以正弦波形式作用于轴承外环。因此，滚动体同一时刻会承受来自多个同频但不同相位和幅值的波形，叠加后作用于轴承内环，波形经调制后会产生倍频或次倍频。取某2个不同的Fri，如图17所示，都可得到内环某点对应的动载荷。换言之，滚动体的碾压对轴承内环形成了不同频率的行波激励。

图16 径向载荷作用下滚动体变形Fig.16 Deformation of rolling body under radial load

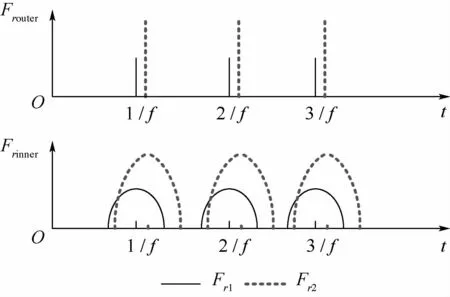
图17 外环与内环载荷传递关系示意图Fig.17 Schematic diagram of load transfer relationship between outer ring and inner ring

此外，轴承中微小几何误差的旋转效应会使得滚动体与滚道的接触关系发生改变，从而引起与各零件特征频率相关的高频激励。由于滚动体的碾压是周期性的冲击，故其不能看作单一简谐波，而是可以通过傅里叶变换展开成无穷级数，在频谱图上相应表现为一簇原点发射线。当轴承的滚动面几何误差叠加时，其相位不同，振动谱线会出现加强或减弱；当误差间存在相对角速度时，还会出现振动波的调制，更为复杂[16]。

因此，轴承滚动碾压形成的激励不仅包括转频，还有支点动载荷分布引起的行波振动频率、轴承特征频率，以及各频率的多次谐波和相互之间的调制作用，这些都是动量轮结构系统的载荷激励。

1.3 其他内部扰振因素

1.1节和1.2节将轮体结构看为一个整体，主要分析了动量轮结构系统的参数激励和载荷激励，即动力学方程式（1）中的M 和Q，本节分析其他潜在的扰振因素。

实际的轮体结构为带有连接界面的非连续系统，为了减小轮辐的局部振动，采用阻尼环结构。阻尼环本身是板壳类零件，包含多个销钉和螺栓紧固件，在阻尼环的不同位置实现轴向、径向和周向3个方向的定位约束。连接结构在受力状态下的离散特性使得在高速旋转时界面接触状态发生变化，一方面影响质量矩阵M 的不确定性，另一方面也会产生不平衡量激励Q。此外，连接结构的装配紧度及阻尼环的材料参数等会影响阻尼矩阵C。而刚度矩阵K的扰动主要来源于支点轴承刚度的非线性，其影响因素为支点动载荷。

2 计算仿真与试验验证

第1节分析了动量轮结构系统的扰振机理，本节主要通过仿真验证轮缘的行波振动形成的参数激励，并通过与试验的结合共同验证支点动载荷与轴承产生的载荷激励。

2.1 实体建模

动量轮结构系统仿真计算模型如图18所示，其采用的实体结构包括轮体、阻尼环和支杆，有限元模型如图18（a）所示，采用实体单元网格划分。轮体为一整体不包含连接结构，将连接件的质量附加于阻尼环上，阻尼环与轮辐设置为绑定接触。边界条件如图18（b）所示，将支杆的一端固定约束，在转子两侧支点处分别设置轴承单元约束，计算动量轮结构系统的Campbell图。

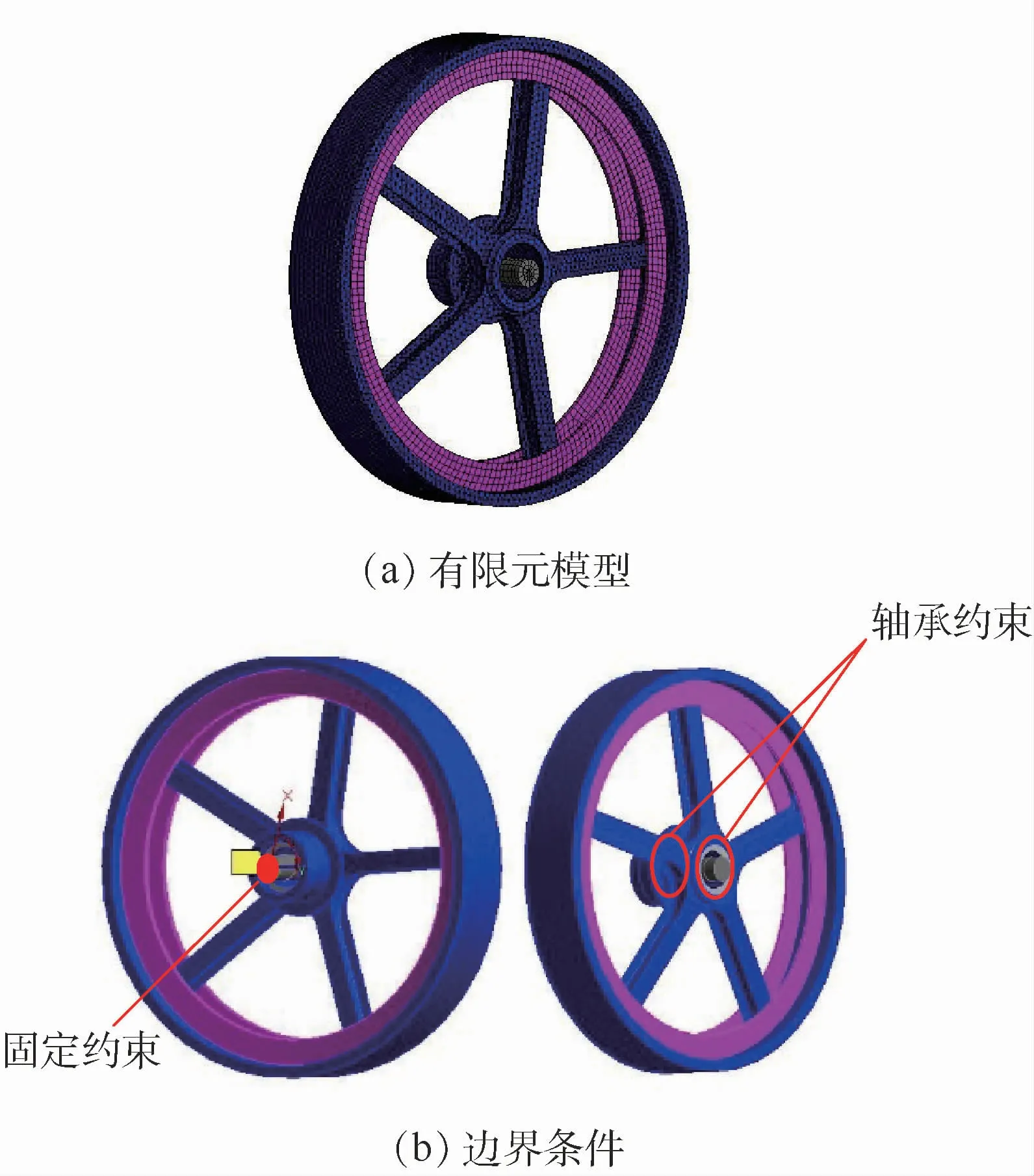
图18 动量轮结构系统仿真计算模型Fig.18 Simulation calculation model of momentum wheel structural system

2.2 仿真结果

动量轮结构系统Campbell图如图19所示。动量轮第1阶模态为动量轮整体径向摇摆，由于轮缘的行波振动，会出现“V”型线。第2阶模态为整体径向平移模态，此时轮缘行波振动的周向波数为1，故前后行波频率理论相同，仍存在微小频率差异的原因是：支杆弯曲变形引起陀螺力矩及阻尼环局部轴向振动在泊松比作用下会有微量级径向振动，相应产生科里奥利力。第3阶模态主要为阻尼环的振动模态及轮体的轴向平移。做出轴承支点动载荷对应的基频激励线，会与一阶反进动模态产生交点；做出轴承滚动碾压产生的二倍频激励线，会与动量轮的一阶进动产生交点，从而激起共振。因此，通过仿真验证了轮缘的行波振动。

2.3 试验验证

为了验证动量轮结构系统存在2.2节所述激励，采用Kistler测力台设备（见图20），测试某典型悬臂支承动量轮结构系统在全工作转速下的输出扰振力，得到振动响应瀑布图。

动量轮结构系统振动响应瀑布图如图21所示。可知，在无外界激励的条件下，存在从原点出发的多条激励曲线，其来源均为结构系统内部，虚线1为与转速同频的支点动载荷，其振动响应最大，基本为二次曲线；虚线2为轴承碾压作用形成的二倍频激励，与一阶正进动交点处响应达到峰值；此外还存在与轴承特征频率相关的激励曲线，每条激励线与各阶模态相交都会激起不同程度的共振，与载荷激励分析相符。试验证明，动量轮结构系统存在明显的前后行波，且频率基本与仿真相符，由于轮体实际含有连接结构会导致频率的微小差别。仿真与试验的综合验证了微振动机理分析的正确性。

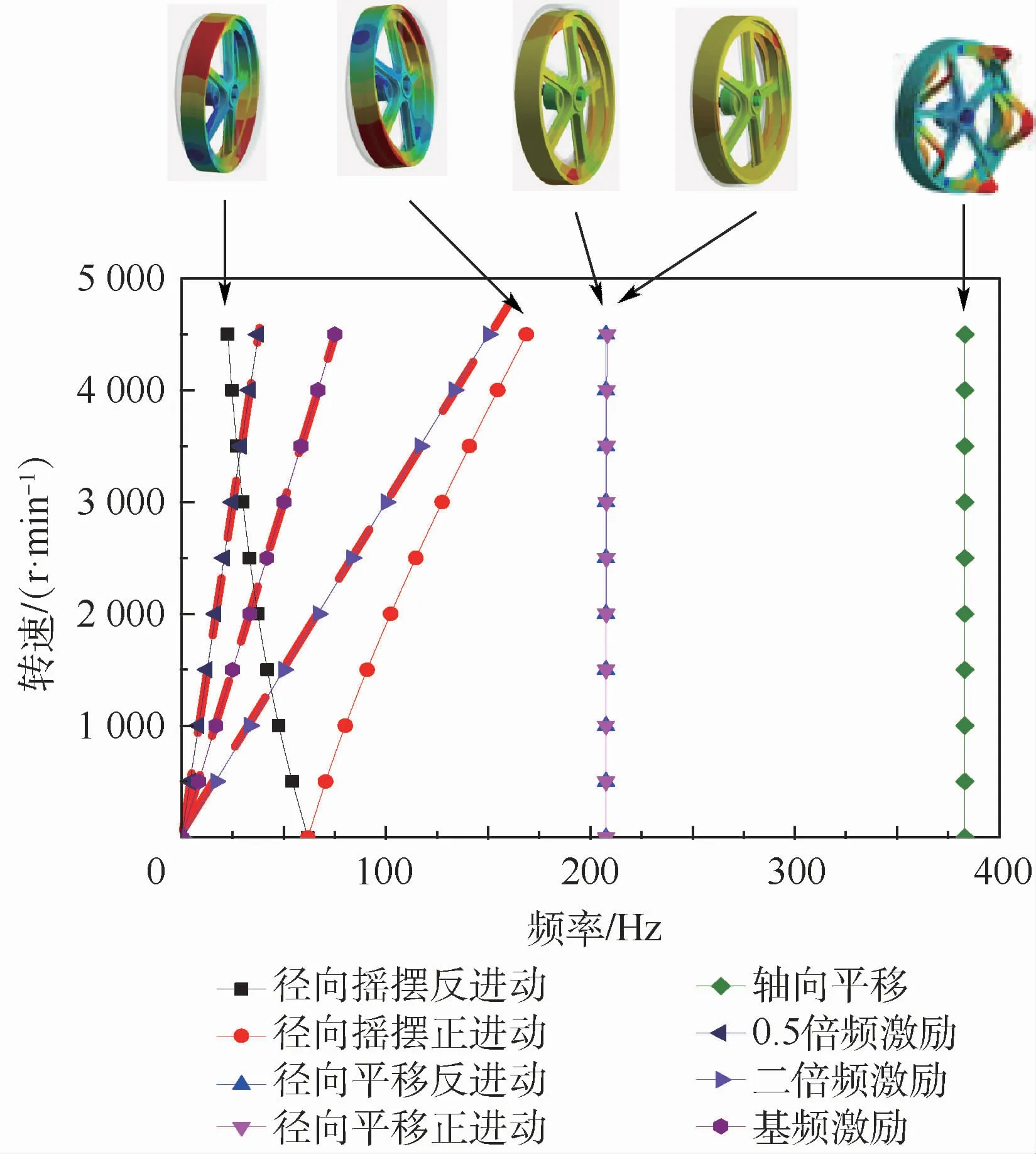
图19 动量轮结构系统Campbell图Fig.19 Campbell diagram of momentum wheel structural system

图20 Kistler测力台设备Fig.20 Kistler dynamometer equipment

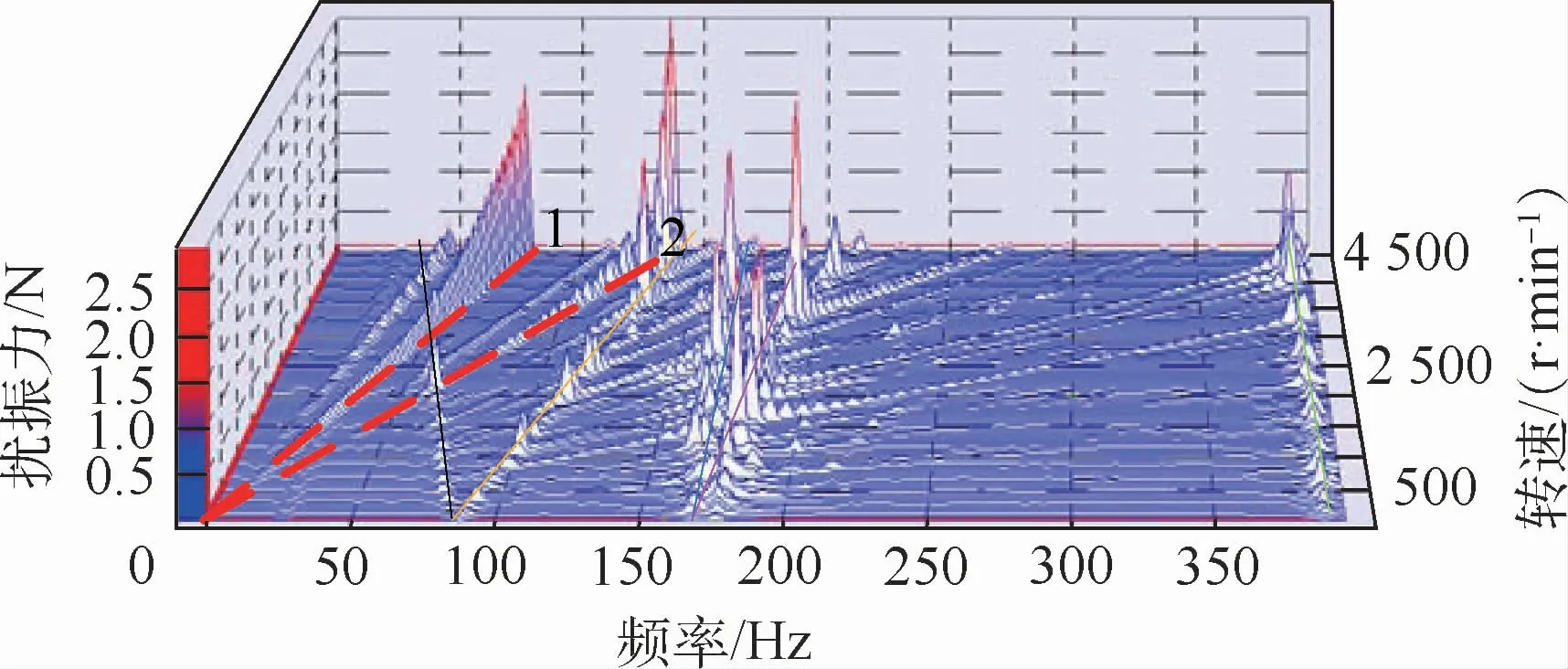
图21 动量轮结构系统振动响应瀑布图Fig.21 Waterfall diagram of vibration response of momentum wheel structural system

3 结 论

本文针对单端悬臂支承方式的动量轮结构系统，从动力学方程的角度，研究其可能引起微振动的激励因素，得到如下结论：

1）轮体结构为轮缘-轮辐的几何形式，使得其具有质量和刚度分布非均匀的特点，轮体的转动惯量会在旋转状态产生与转频相关的微小变化，这种微变形成为结构参数激励。

2）轮体结构中轮缘部分的局部变形主要为径向，会产生科里奥利力的作用改变局部刚度，使得转动惯量产生与行波频率相关的微小变化，这种微振动成为结构参数激励。

3）由于动量轮结构系统的支承方式不对称，更容易发生内部支杆的弯曲，而轮体上的惯性力矩会产生支点动载荷作用在轴承上，与转频成二次方关系。而由于轴承结构的不连续，会将支点动载荷发散成高次谐波传递到支杆结构上，共同作为结构系统的载荷激励。

4）实际动量轮结构中还存在其他存在内部激励源，如连接界面的装配误差会影响阻尼等结构参数，轴承刚度的非线性会影响刚度等结构参数。

5）通过仿真验证了行波振动引起的参数激励；通过与试验相结合验证了支点动载荷及轴承引起的高频载荷激励。