基于速度障碍法的飞行冲突解脱与恢复策略

王泽坤，吴明功，温祥西，*，蒋旭瑞，高阳阳

（1.空军工程大学 空管领航学院，西安710051； 2.国家空管防相撞技术重点实验室，西安710051；3.中国人民解放军94116部队，和田848000； 4.中国人民解放军93175部队，长春130051）

目前的空中交通管制系统是一个典型的“人在回路”决策系统，难以突破管制员的负荷极限，并且人因误差无法避免，同时使得空中交通管制运行难度增大，不利于飞行冲突预先调配。冲突探测与解脱技术（Conflict Detection and Resolution，CD＆R），能够对航空器小于安全间隔的趋势进行先期预警，并提供高效的解脱方案，是空中交通管制系统中的一项关键技术，对确保航空器的飞行安全发挥着重要作用。该领域的研究已相对成熟，多种方法被应用在该问题中，目前工程领域应用最多的是几何法。

早在2000年Bilimoria就提出一种几何优化方法[1]，并应用于未来空中交通管制理念评价工具（FACET）项目[2]。Hwang等[3]在飞机能获取周围所有的飞行信息的前提下，提出一种几何优化方法。文献[4-5]利用飞机当前位置和速度矢量信息进行飞机冲突解脱的几何优化方法，仅通过航向变化或速度变化即可有效解决飞行冲突，并使得解脱轨迹与标称轨迹的偏差最小。文献[6-8]关注了解脱后的航迹恢复问题，将飞机重新定向到其原始目的地，而不引起新的冲突。但是并没有给出各航段飞机的偏航角度以及时间或者距离，不便于操作。

2008年Berg等[9]首先介绍了基于互惠速度障碍（RVO）的自主避障几何方法，并在文献[10]中提出最优互惠避障（ORCA）算法。由于速度障碍法实现简单且从几何上易于理解，在UAV自主避障算法中得到了很好的应用。Durand和Barnier[11]首先在飞机冲突探测与解脱方面引入速度障碍法，通过获取对方飞机的位置和速度信息（ADS-B），以期解决潜在的飞行冲突。Durand和Barnier[11]将机器人的一种自分离算法应用于飞行环境中，提出解脱策略，之后Durand等[12]提出基于位置和速度的分析方法。

现有的速度障碍避障算法[13-14]，多用于UAV系统自主避障。但是该算法仍存在以下不足：①算法较为复杂，飞机的速度和航向以计算周期为步长，持续变化；②如果飞行速度受到约束，速度相似的飞机以较小的角度汇聚飞行时，它们倾向于选择平行轨道，使得飞机远离目的地，而不是解决飞行冲突。

而执行航线飞行的航空器应尽量避免多次改变速度大小和方向，减少飞机机动次数，并确保飞行安全。

因此本文将基于速度障碍法，对飞行冲突进行深入研究，在之前工作的基础上[15-16]，基于几何优化和最少机动（解脱和恢复两次机动），建立航空器之间的飞行冲突解脱和航迹恢复几何模型，应用于航路（航线）中飞行的冲突，这在实际运行中将极大减轻管制员工作压力，减少工作负荷。

1 模型简化

结合民航航班飞行相关规定和空中交通管制运行特点，模型设计作出以下简化：

1）航路飞行过程中，飞机速度基本保持不变，即在冲突解脱时，假设飞机速度相同（同向飞行除外）。

2）飞机在爬升和下降阶段地速保持不变。

3）由于本文冲突解脱过程中飞机速度和航向改变量都较小，视其为瞬间改变。

4）雷达管制条件下，航路航线飞行中，为了防止飞行冲突，保证飞行安全，提高飞行空间和时间利用率，规定的航空器之间应当保持最小安全距离。飞行间隔包括垂直间隔和水平间隔。其中水平间隔dl=10 km，垂直间隔dv=300 m，并且水平和垂直方向上的安全间隔至少要满足一项。因此，本文采取圆柱形安全保护区模型，如图1所示。

图1中安全保护区运用公式为

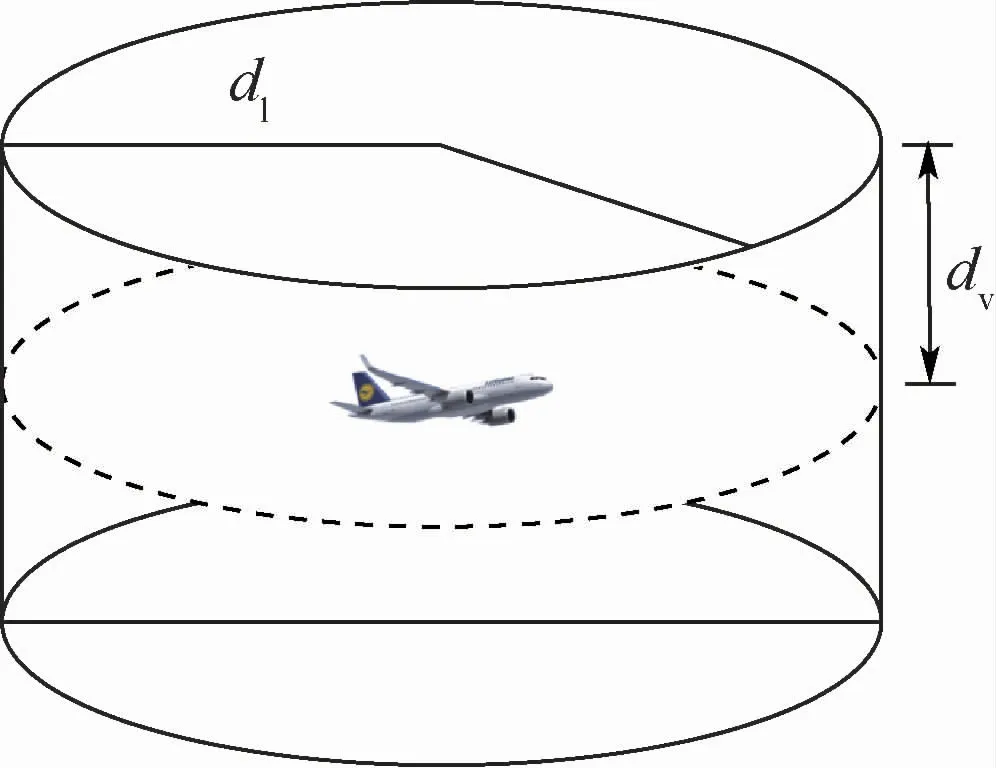
图1 安全保护区模型Fig.1 Safety protection zone model

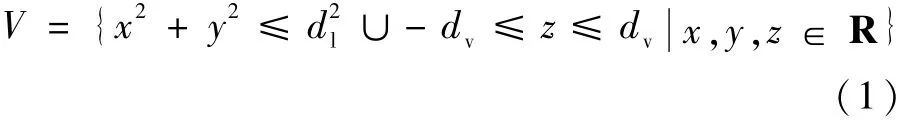
式中：V为安全保护区。

2 探测模型

2.1 速度障碍模型

速度障碍法定义了一个相对速度障碍区域，当相对速度落入该区域时则视为两机之间在约束的时间内会发生飞行冲突。为解决该冲突，相对速度沿最短路向冲突区外解脱。

如图2所示，AC1、AC2表示飞机，AC1速度为v1，AC2速度为v2。α为两机之间连线AB与速度障碍区边界之间的夹角，即速度障碍区顶角的一半，γ为AB与相对速度vR之间的夹角。

定义1 相对碰撞区（Relative Collision Cone，RCC），即飞机会发生碰撞的相对速度vR=v1-v2的集合。

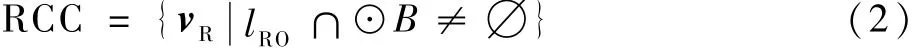
式中：lRO为相对速度所在直线；⊙B为AC2的安全保护区。

该模型只考虑飞机之间的位置关系和当前的状态，以AC2为参照点，AC1作相对运动，若AC2的保护区与AC1的相对运动轨迹有交叉，则两机之间会发生飞行冲突，否则无飞行冲突。

因此可以对两机飞行冲突作出如下判断：当α＞γ时，两架飞机存在飞行冲突；当 α≤γ时，两架飞机不存在飞行冲突。

α和γ的大小可以分别由式（3）和式（4）给出：

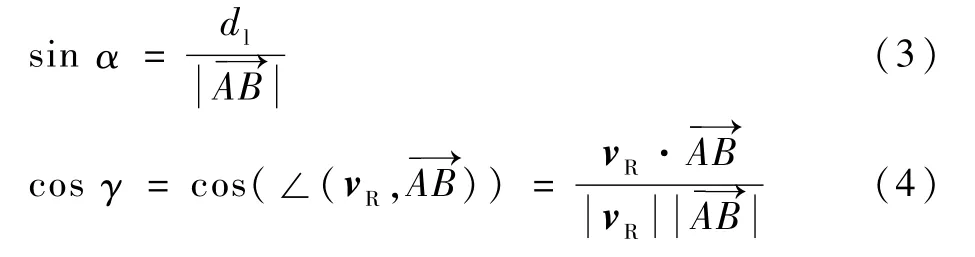
图2 速度障碍模型Fig.2 Velocity obstacle model

2.2 有时间约束的速度障碍模型

速度障碍模型只考虑相对速度与速度障碍区的关系，空域内每两架飞机之间的飞行冲突都需要进行冲突解脱，算法相对复杂，可操作性不强。

在空域内飞行流量大，飞机密度较高时，如果速度障碍模型不施加以时间约束，会导致每架飞机承担的冲突解脱数量过大，甚至无法进行解脱。因此，提出时间约束下的速度障碍模型。引入时间参数τ，即在设定的时间 τ内，飞机AC1和AC2会产生飞行冲突，如图3所示，图中P点坐标为（PB-PA）/τ；⊙P半径为dl/τ；飞机AC2的安全保护区半径为dl。

AC1相对于AC2的速度障碍区可表示为

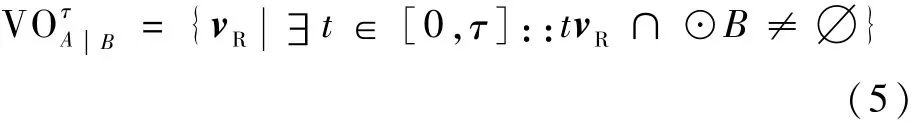
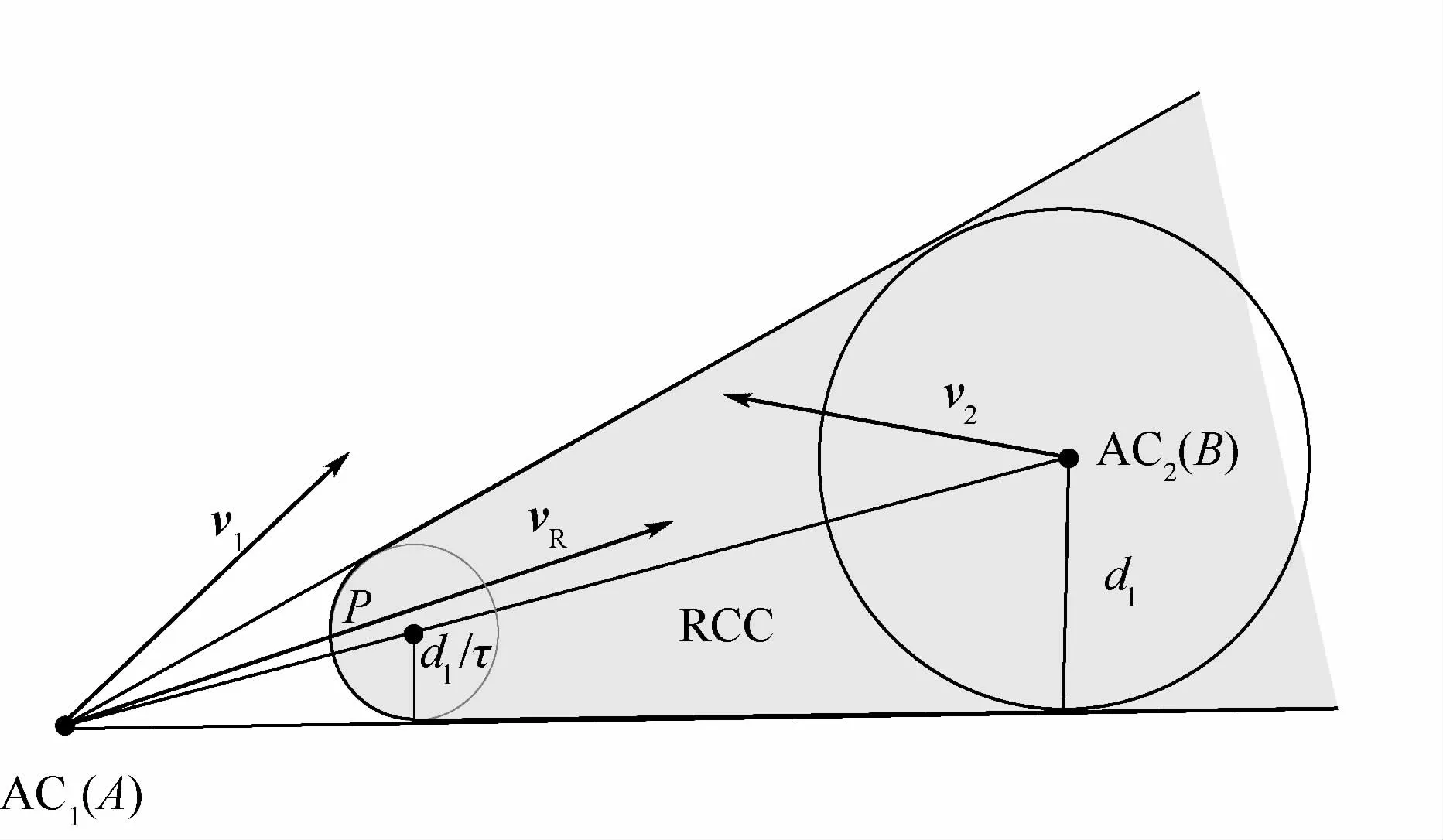
图3 有时间约束的速度障碍模型Fig.3 Velocity obstacle model with time constraints

3 双机冲突解脱模型

管制运行中，实施飞行冲突解脱策略主要分为3种：高度解脱（Elevation Resolution，ER）、速度解脱（Speed Resolution，SR）和航向解脱（Heading Resolution，HR）。

3.1 高度解脱

AC1与AC2两架飞机处于同高度层，起始坐标分别为（x1，y1）、（x2，y2），AC1若想超越AC2飞行，则可以采取改变高度层的策略解决飞行冲突，如图4所示。在高度层改变的过程中，需要一直保持两机之间在水平和垂直方向上，至少有一个间隔满足最小安全间隔（水平安全间隔为10 km，垂直安全间隔为300 m），假设在整个过程中，飞机的地速始终保持不变。为了简化计算过程，将AC2作为参考系，则AC1的相对速度vR=v1-v2，给定AC1的上升/下降率为v⊥。

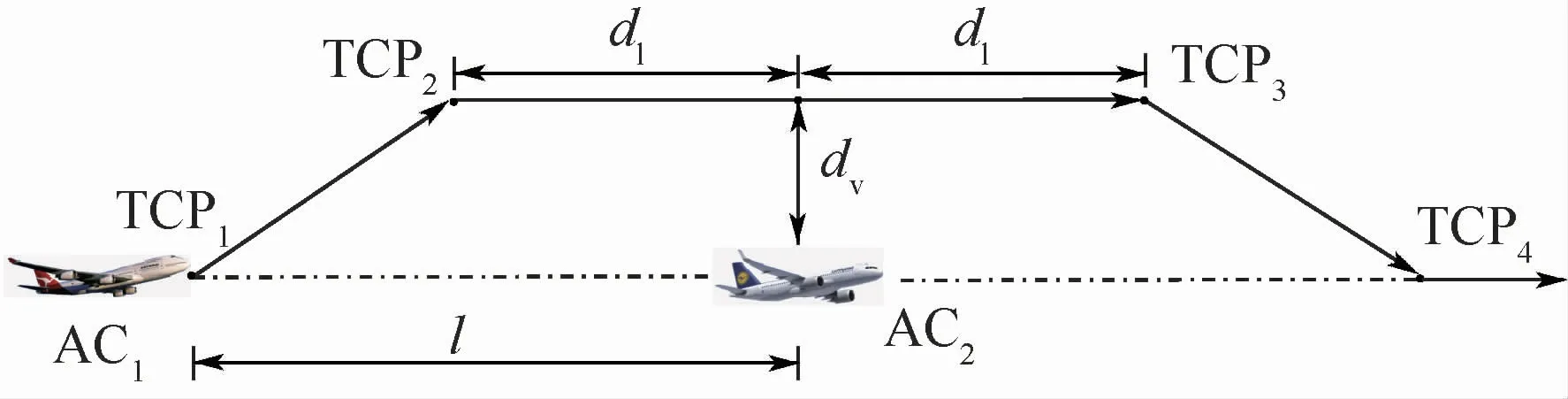
图4 高度解脱Fig.4 Elevation resolution

TCP1→TCP2：结合两机速度以及安全间隔，可以得到该段航迹：

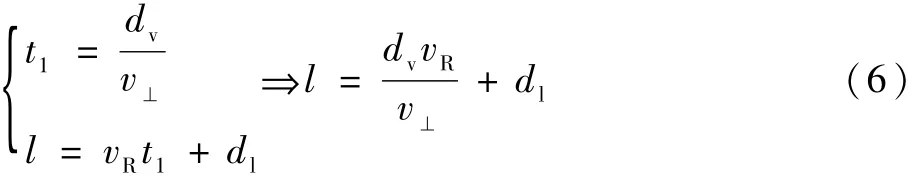
AC1与AC2之间的距离为l时，开始上升高度（TCP1），当上升高度为两机之间的垂直安全间隔时改为平飞（TCP2）。

TCP2→TCP3：为满足AC1与AC2之间始终保持安全间隔，当水平方向上两机之间的间隔为dl时，AC1开始下降高度（TCP3）。

即AC1在该阶段飞行的时间为

TCP3→TCP4：该段为下降阶段，AC1按给定的下降率下降高度至原飞行高度层。

使用高度解脱时，两机之间的位置关系必须满足：

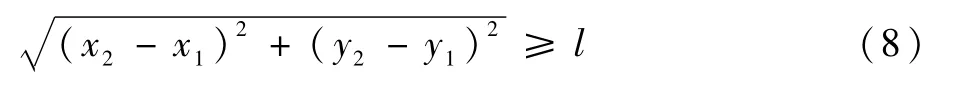
将式（6）代入式（8）得

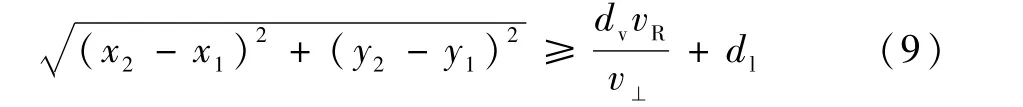
3.2 速度解脱

3.2.1 解脱冲突

如图5所示，AC1和AC2分别以v1、v2向前飞行，AC1相对于AC2速度为vR=v1-v2。图中θ1为v1与两机连线之间夹角，θ2为v2与两机之间连线夹角；β为vR与速度障碍区边界夹角；ε为v2与速度障碍边界夹角；φ为v1与速度障碍边界夹角。根据速度障碍法的冲突判别标准，显然，两机之间存在冲突。在此场景中，采取改变v1大小的策略，使得新的相对速度v′R=v′1-v2，方向指向冲突区边界。

以AC2为坐标原点，以进行冲突解脱瞬间，AC2指向AC1方向为x轴正向，建立惯性坐标系。

在△OMN中，由正弦定理可知：

式中：各角度关系为

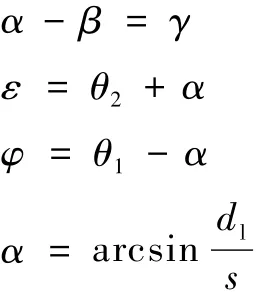
即AC1速度改变量为

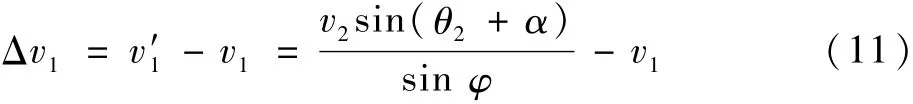
AC1和AC2的初始位置分别为（x1，y1）、（x2，y2），即两机在进行冲突解脱瞬间的距离为

为了便于求解解脱阶段和恢复阶段的飞行时间，改动坐标系后如图6所示，此时AC2坐标

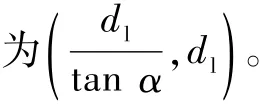
直线GP表达式为

直线GQ表达式为

直线PQ表达式为

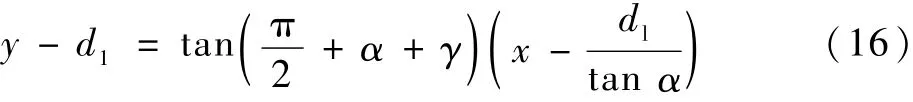
P点坐标（xP，yP）可以由以下推导得出：

联立式（14）和式（16）得

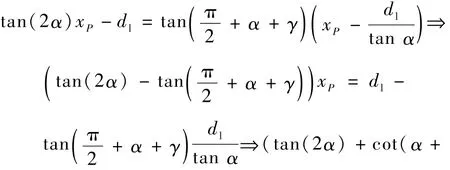
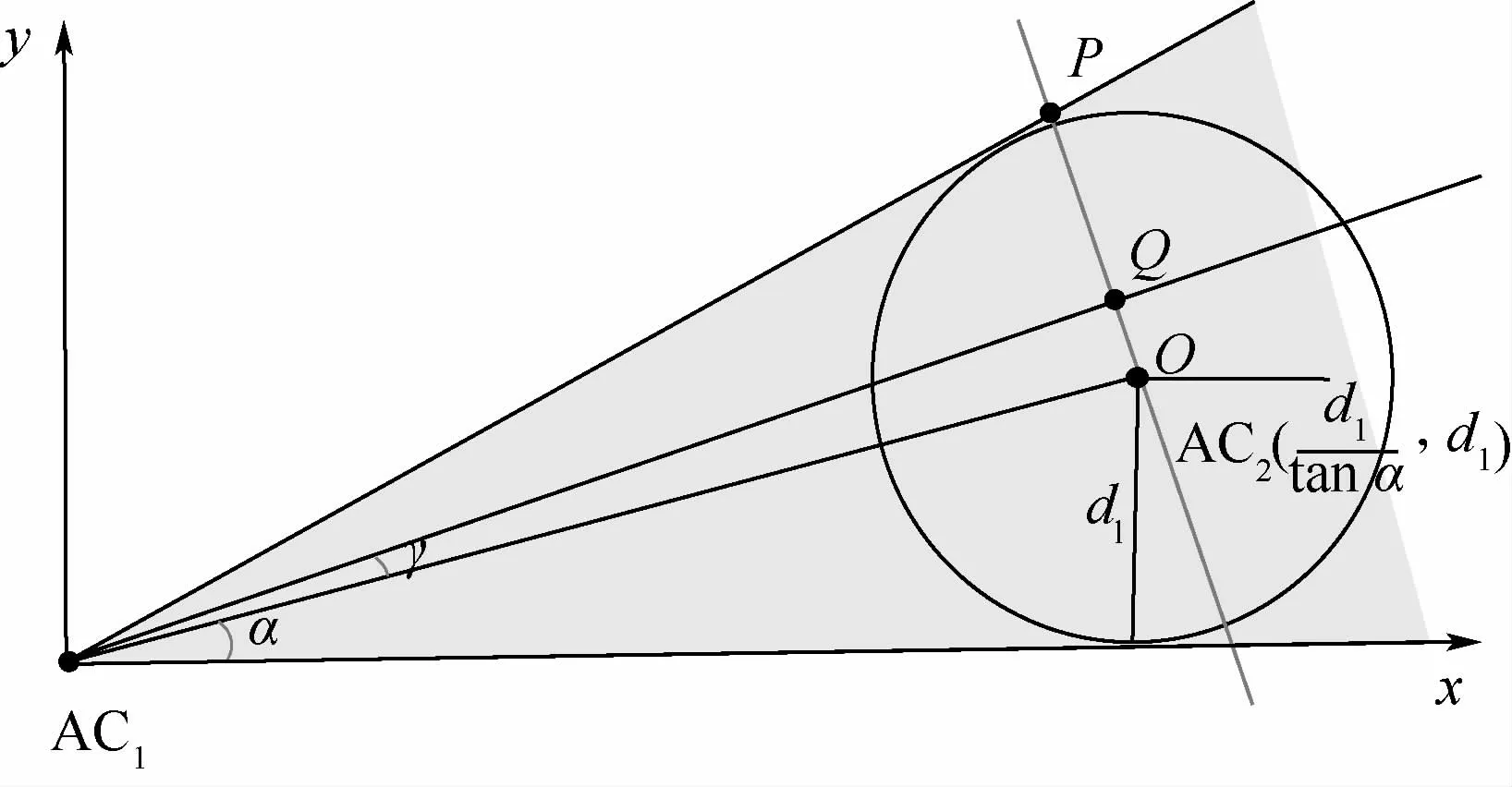
图6 飞机相对位置示意图Fig.6 Schematic diagram of relative position of aircraft

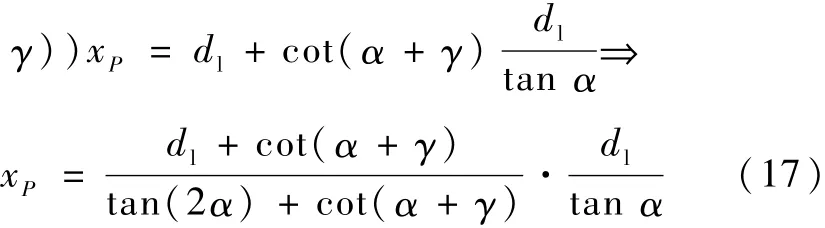
代入式（14）或式（16）可得

3.2.2 恢复航迹

到达航迹恢复点P后，AC1航向左转，使得相对速度左转角度为2β，切入原航线后恢复原航向，直飞目的地，如图7所示。

即AC1速度改变量为

由于飞机性能的影响，飞行速度不能无限制增大或减小，假设AC1调速范围为，即 当，才可以采取速度解脱策略。

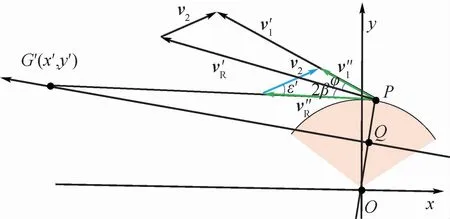
图7 速度解脱航迹恢复Fig.7 Track recovery with speed resolution

3.3 航向解脱

3.3.1 解脱冲突

如图8所示，AC1和AC2分别以v1、v2向前飞行，AC1相对于AC2速度为vR=v1-v2。根据速度障碍法的冲突判别标准，显然，两机之间存在冲突。在此场景中，采取改变v1的方向的策略，使得新的相对速度v′R=v′1-v2，方向指向冲突区边界。

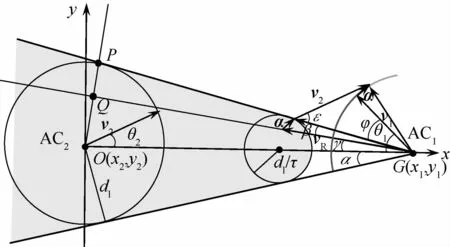
图8 航向解脱Fig.8 Heading resolution

由于两机速度大小相同，且AC1仅改变速度方向，不改变大小：

假设AC1航向改变角度为 Δθ1，此时相对速度方向与AC2保护区相切：

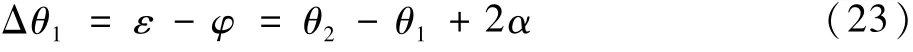
3.3.2 恢复航迹

对比速度解脱过程，明显可以看出，采取航向解脱时，相对速度方向和采取速度解脱策略恢复航迹时一致，因此，AC1同样飞至P点（3.2.1节已给出坐标），然后改变航向，恢复原航迹，如图9所示。

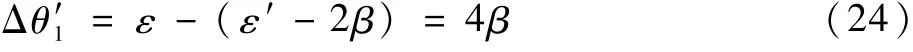
式中：

图9 航向解脱航迹恢复Fig.9 Track recovery with heading resolution

4 双机冲突解脱策略

在飞行过程中，同高度层的冲突模型总结下来，有以下3种：同向航迹飞行冲突、交叉航迹飞行冲突、逆向航迹飞行冲突，不同冲突类型都有不止一种解脱策略。秉承航迹支付代价最少的原则，在冲突解脱过程中，优先考虑速度解脱的方式，其次是高度解脱，由于改航会引起较大的航程支付代价，该策略放在最后考虑。

进行冲突解脱时，为保证飞行任务的完成，同向和逆向航迹飞行冲突暂不考虑速度解脱策略。并且由于高度以及速度解脱需要满足一定的飞行条件才能够实施，将航向解脱视为最终的冲突解脱选择方案，当高度和速度解脱得条件均不满足要求时，即可采取航向解脱策略。具体选择流程如图10所示。

4.1 同向航迹飞行冲突（0°～45°）

定义2 航迹交叉角小于45°的飞行称为同向飞行。

若后机速度大于前机，即后机将飞跃前机，两机之间的距离s≥l，则可以改变高度层以避免飞行冲突。

若两机之间的距离s＜l，则改变航向以避免飞行冲突。解脱过程仅考虑x轴方向上的速度和位置关系，则

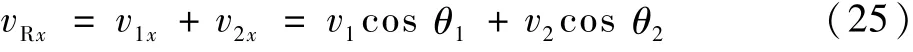
由式（6）可知：

4.2 交叉航迹飞行冲突（45°～135°）

定义3 航迹交叉角在45°～135°之间的飞行称为交叉飞行。

此时若s≥l，则采取高度解脱策略进行冲突解脱，否则采取航向解脱策略以避免飞行冲突。

4.3 逆向航迹飞行冲突（135°～180°）

定义4 航迹交叉角大于135°的飞行称为逆向飞行。

若两机之间的距离s≥l，且存在逆向航迹飞行冲突，则首先改变高度层以避免飞行冲突。解脱过程仅考虑x轴方向上的速度和位置关系，高度解脱的安全距离l计算方法同4.1节。

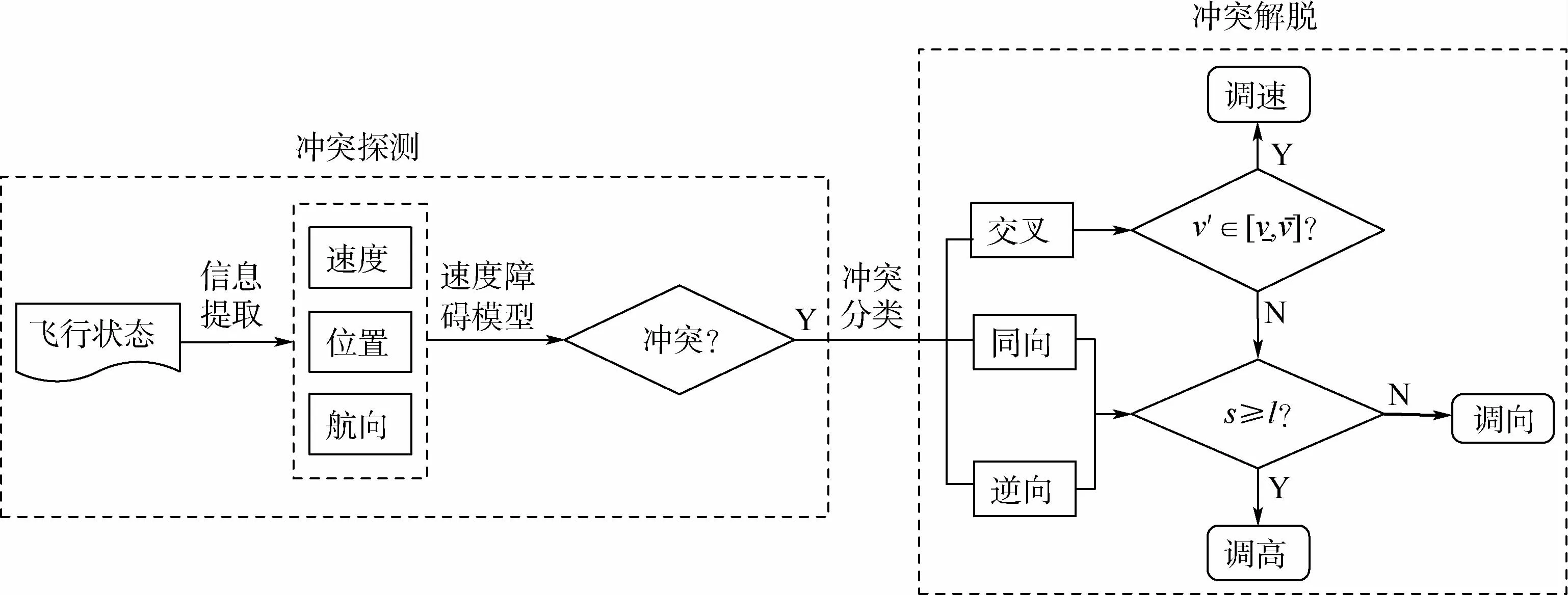
图10 双机冲突解脱流程Fig.10 Collision resolution process of two aircraft

若两机之间的距离s＜l，则采取航向解脱策略以避免飞行冲突。

5 算例分析

为了验证本文冲突解脱策略的有效性，本节运用MATLAB：R2016a环境进行仿真分析。其中每架飞机已给定起始坐标以及速度大小，初始航向已经给出，并且假设当前的飞行高度层为4200 m，时间约束 τ=0.05 h。

根据空中交通管制运行特点和《中国民用航空飞行规则》中的相关规定，保证实际工作中的可操作性，解脱过程中的部分参数已经给定：①为保证旅客安全舒适的乘机条件，上升和下降的垂直速度通常不大于3 m/s；②改变速度解脱策略中，飞机速度限制为[600，900]km/h。

首先根据飞机位置和速度信息，判断其冲突类型以及各类解脱条件是否满足，选取相应的冲突解脱策略。表1给出了4对飞机的位置信息。

针对表1中各场景的飞机位置和速度信息，可根据第4节内容对飞行冲突作出简单判断，并给出具体的解脱策略，选择过程如表2所示。

为了验证方法的有效性，对上述例子进行仿真实验，每个场景中，均给出两架飞机的飞行轨迹，以及两机之间的间隔。

图11展示了第1种情景，AC1和AC2相距一定距离并以相同航向飞行，其中，AC1从（0，200，4.2）km开始，速度为800 km/h，而AC2从（110，200，4.2）km开始，速度为700 km/h。在冲突避免过程时，无论上升和下降，两机在水平和垂直安全间隔中始终保持至少有一项满足，即在不引起新的飞行冲突的情况下，AC1完成超越，并返回原航线飞行。

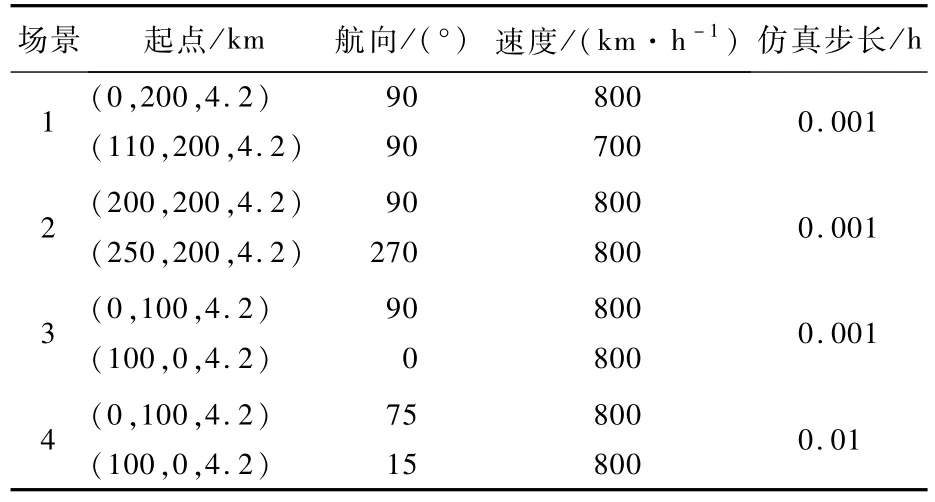
表1 位置信息Table 1 Position information

第2个场景是AC1和AC2相距一定距离，以相同的速度直接相向飞行。AC1起点为（200，200，4.2）km，航向90°，AC2起点为（250，200，4.2）km，航向270°，如图12所示，该场景采取了航向改变的解脱方式。

本文运行的第3个场景是速度相同的两架飞机以90°相交。如图13所示，AC1起点为（0，100，4.2）km，航 向90°，AC2起 点 为 （100，0，4.2）km，航向0°，该场景采用了高度改变的解脱策略，并且保证了两机在水平和垂直安全间隔中始终保持至少有一项满足。

场景4与场景3飞机的初始位置相同，但AC1航向为75°，AC2航向为15°，如图14所示，该场景的解脱策略为速度解脱。在该图中，速度变化可以通过每个时间步长的位置标记来识别。在整个路径中，解脱和恢复部分速度较慢，一旦冲突解决，速度就会恢复到原来的值。

为了满足实际管制指挥需要，仿真过程中，对AC1飞行状态发生改变的冲突解脱点（Conflict Resolution Point，CRP）、航迹恢复点（Track Recovery Point，TRP）、切入原 航迹点 （Cut-In original track Point，CIP）也进行了记录，如表3所示。

由于在解脱过程中未涉及高度层的改变，场景2、场景4中仅给出两机之间的水平间隔，不难看出，AC1在以上飞行过程中均采取两次机动的方式完成冲突解脱与航迹恢复，并且始终保证两机之间的水平间隔不小于10 km。同时在以上仿真中可以看出，由于引入了时间约束τ，各飞机对之间先按原航线飞行，在到达时间约束内时，开始进行解脱，飞机不需要过早的调整姿态，避免空域资源占用过多，缩短了解脱时间。在与原航程对比时发现，速度解脱并不会引起飞机航程的增加，而且经过计算，采取高度策略对航程的改变几乎可以忽略不计，仅在航向解脱过程中会带来航程的增加，比如场景2中解脱后的航程与原计划航程相比，增加了4.4 km，但是对于整个飞行任务来说，这是可以接受的。

表2 策略选取Table 2 Strategy selection

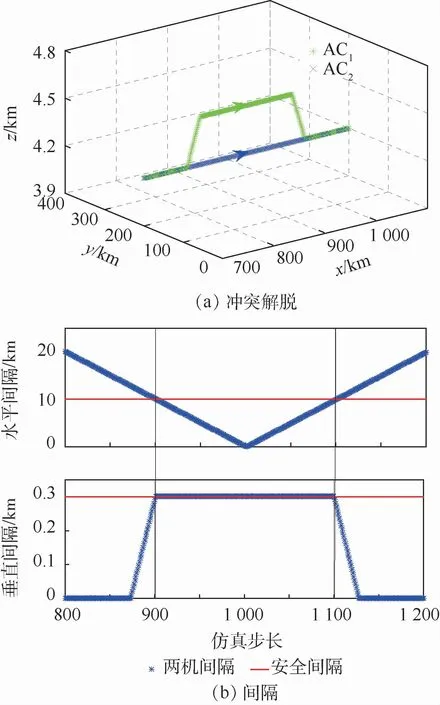
图11 同向飞行高度解脱（场景1）Fig.11 Elevation resolution for the same track of flight（Scene 1）

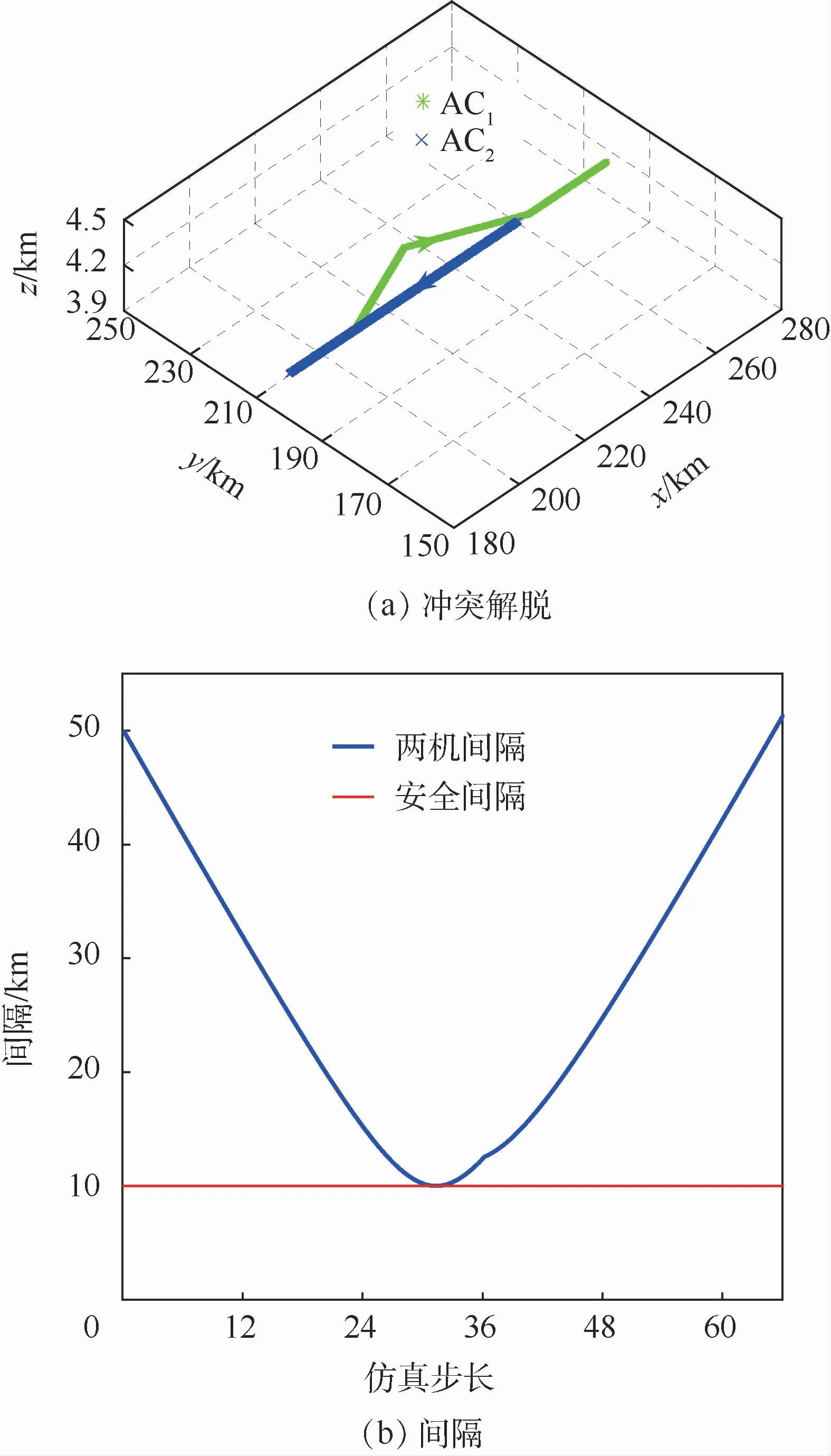
图12 逆向飞行航向解脱（场景2）Fig.12 Heading resolution for opposite track of flight（Scene 2）

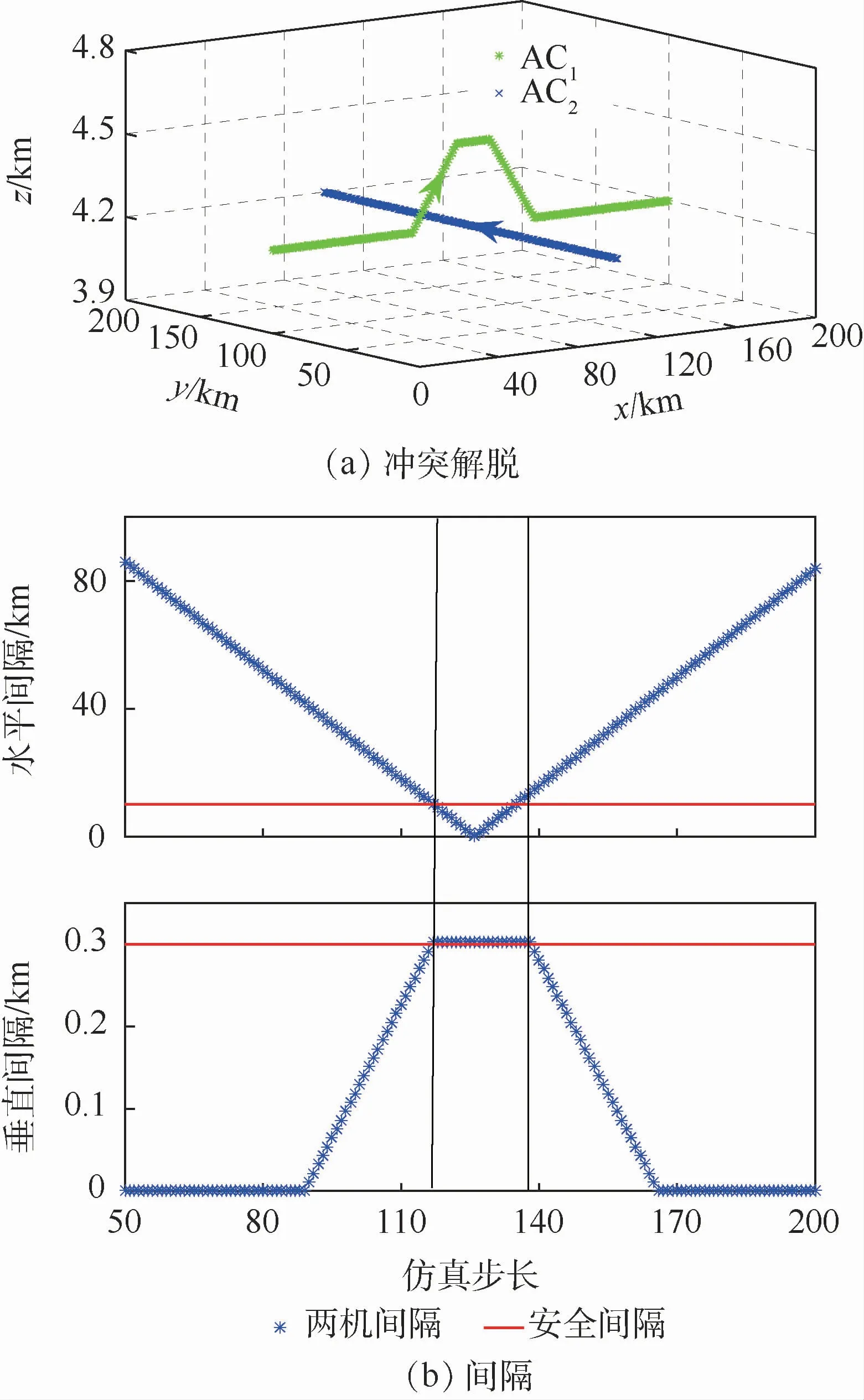
图13 交叉飞行高度解脱（场景3）Fig.13 Elevation resolution for cross track of flight（Scene 3）

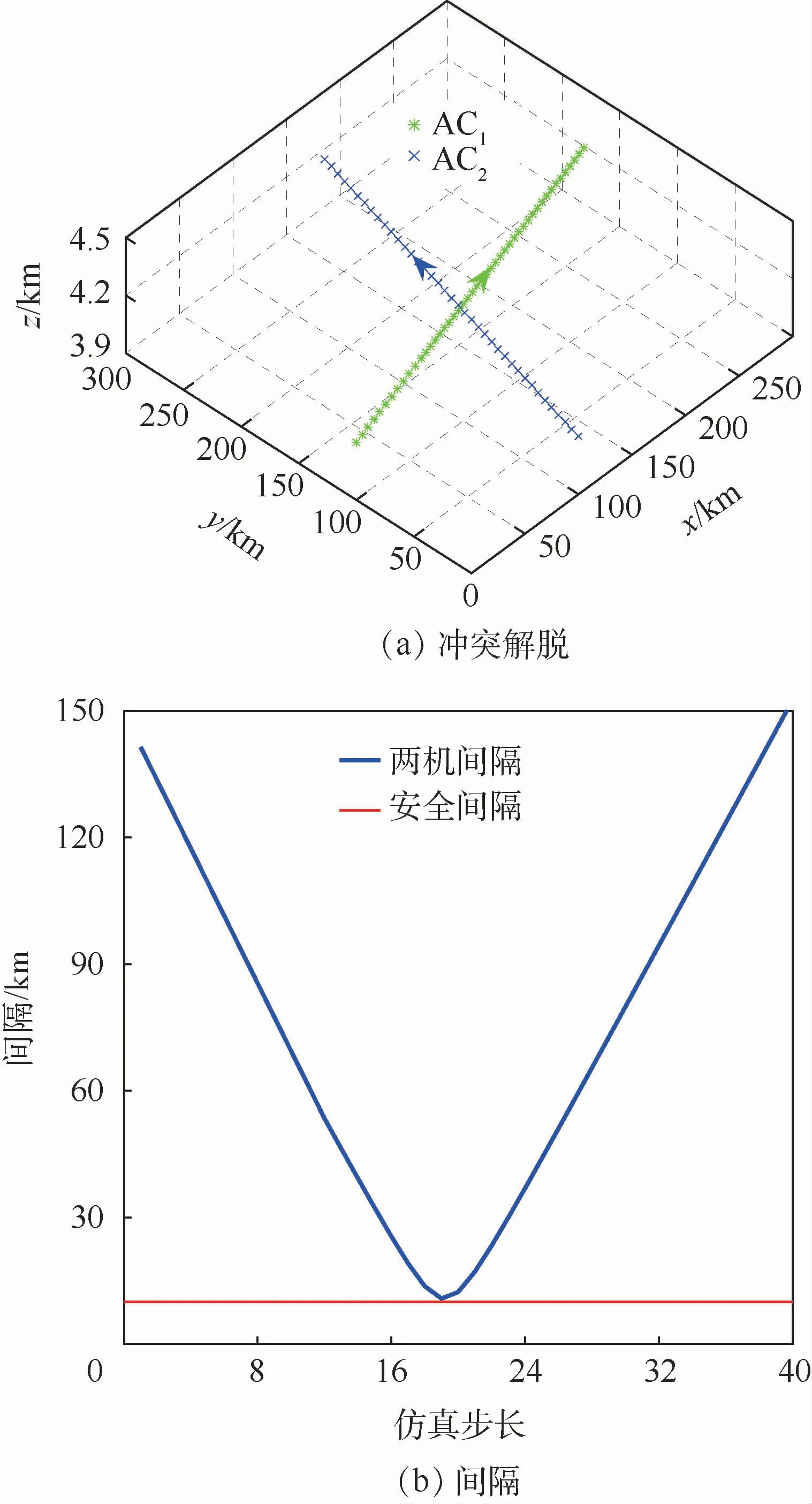
图14 交叉飞行速度解脱（场景4）Fig.14 Speed resolution for cross track of flight（Scene 4）

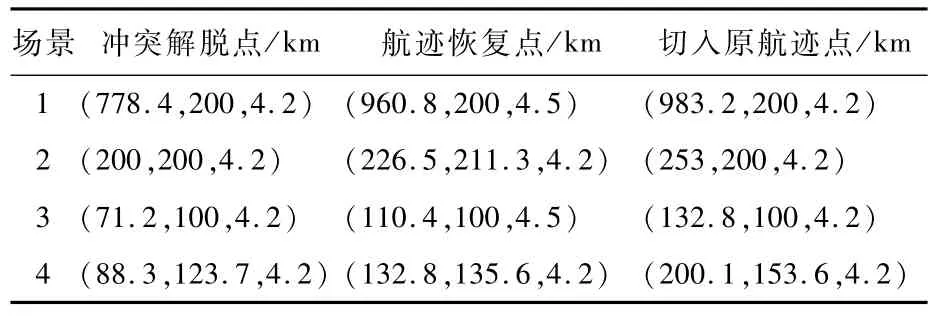
表3 飞行状态改变点Table 3 Flight state change point

6 结 论

本文提出了一种适用于两架飞机的冲突解脱和恢复算法。给定关于这两架飞机的情况以及位置和速度矢量的一些合理假设，该算法将提出一种对自己飞机的机动选择，每个机动包括一个解脱轨迹和一个恢复轨迹，同时在整个过程中与入侵者保持安全间隔。然后对问题进行了严格的数学描述，并证明了算法的有效性。详细展示了“高度解脱”、“速度解脱”和“航向解脱”3种策略，也就是说，对于算法中的冲突解脱，只有对应的航向、速度或高度可以改变，其他参数保持不变，航迹恢复也是如此。最后通过仿真分析验证了该方法的有效性，模型简单可靠，为飞行冲突提供了探测与解脱方法，并具体给出飞行过程中的冲突解脱（探测）点和航迹恢复点的位置。该方法的提出不仅能够帮助管制员进行飞行冲突调配，同时也能辅助飞行员对于飞行冲突解脱作出决策。