基于MBD与Petri网融合的配电网故障定位方法

陈婷，朱文强

(1.福建水利电力职业技术学院，福建 永安 366000；2.福州大学 电气工程与自动化学院，福建 福州 350116)

配电网是直接与用户相连的系统，其安全稳定运行直接影响到人们的日常生活，关系到整个电力系统的可靠性[1-2]。快速、高效的配电网故障诊断方法是配电系统安全、可靠运行的重要保证。

目前，配电网故障诊断方法有很多，主要可以分为两类：一类是人工智能算法，主要包括遗传算法[3]、粒子群算法[4]、免疫算法[5]、和声算法[6]、专家系统[7-8]等；另一类是基于图论的矩阵算法[9-11]。其中，人工智能算法在配电网中的应用已成为研究的热点。为了克服传统的专家系统对知识依赖性强、不能诊断经验之外故障的缺点，自20世纪70年代以来,Reiter和其他国外学者提出了基于模型诊断(model-based diagnosis，MBD)的方法。目前，MBD方法已经成为人工智能领域一个重要的分支，被广泛应用在各个领域。文献[12-13]将MBD方法应用在牵引变电站的故障诊断中，建立变压器正常运行和故障情况下的模型，利用MBD一致性推理和溯因推理实现变压器外部故障的诊断。文献[14-16]在配电网系统中，利用MBD方法进行故障诊断，但是由于溯因推理诊断模型的复杂性及低效率,导致实际应用效果很差。

Petri网是以图像化方式建立模型，在描述系统的并发、异步或循环发生的事件方面具有优势，且建模简单、效率高，在电网的故障诊断中已经有相关的研究[17-20]。为了解决MBD故障诊断过程中，基于溯因推理建模的复杂性和低效率的问题，本文提出一种将MBD一致性推理与Petri网融合的配电网故障诊断方法，并对某10 kV配电网实例建模仿真。

1 MBD诊断方法基本原理

MBD诊断方法是使用系统内部结构和行为知识进行系统诊断，其基本思想如图1所示。

图1 MBD的基本思想Fig.1 Basic idea of MBD

1.1 MBD诊断方法的基本理论

MBD诊断方法的基本理论包括以下3个方面：

a)待诊断系统。可以用一个三元组(JSD、JOBS、JCOMP)来表示一个待诊断系统，其中，JSD、JOBS和JCOMP分别表示系统的模型描述、观测值和系统的元件集合[14-16]。

b)冲突集CCS。待诊断系统的冲突集是一个元件集合{c1,c2,…,ck}，需要满足以下条件：

(1)

式中：F(ci)表示元件ci有故障，┐表示“否定”。⊆和∪分别表示包含和并集。

c)最小冲突集CMCS。如果任意真正冲突集的子集是不冲突,那么就是一个最小冲突集。

d)碰集CHS及最小碰集CMHS。设Cg是冲突集簇，则满足以下条件：

(2)

若一个碰集的任何一个真子集都不是碰集，那么它是一个最小碰集。

e)诊断。MBD诊断方法可分为基于一致性推理诊断和基于溯因诊断。系统所有最小冲突集的最小碰集即为系统的一个诊断。

1.2 基于MBD一致性理论的配电网故障诊断方案

由于配电网系统中各个电压、电流互感器的分布位置一般是固定不变的,结合上述MBD的基本理论，本文将参考文献[15]中的方法将其应用于配电网的故障诊断，并给出一个诊断方案，具体步骤如下：

a)抽象系统元件。MBD故障诊断主要考虑的元件对象是母线和输电线路。如图2所示，L1、L2表示馈线区段，对应的阻抗为Z1和Z2；B1、B2、B3表示配电母线；M1、M2、M3表示测量信息点。

图2 配电网分析图Fig.2 Analysis diagram of distribution network

b)建立解析冗余关系式。以图2配电网为例，根据基尔霍夫定律和配电网拓扑结构关系得出各个元件的正常约束关系，即为解析冗余关系。例如：写出馈线区段L2的三相解析冗余关系为：

U3A-U2A+Z2AI3A=0.

(3)

-I2A+I3A=0.

(4)

U3B-U2B+Z2BI3B=0.

(5)

-I2B+I3B=0.

(6)

U3C-U2C+Z2CI3C=0.

(7)

-I2C+I3C=0.

(8)

式(3)—(8)中：U2A、U2B、U2C分别为区段L2的三相电压；U3A、U3B、U3C分别为区段L3的三相电压；I2A、I2B、I2C分别为区段L2的三相电流；I3A、I3B、I3C分别为区段L3的三相电流；Z2A、Z2B、Z2C分别为区段L2的三相阻抗。下文中同类符号的意义以此类推。

c)冲突识别。每个解析冗余关系是指仅包含系统可观测变量，从配电网模型中得出的约束方程，存在一个最小支撑环境，利用配电网的结构与系统状态监测信息的分布固定不变的特点，采用改进遗传算法[16]找出所有最小冲突集候选。如式(3)、(4)的最小冲突集候选为{L2A, B2A}；式(5)、(6)的最小冲突集候选为{L2B, B2B}；式(7)、(8)的最小冲突集候选为{L2C, B2C}，其中L2A、L2B、L2C分别为区段L2的三相线路；B2A、B2B、B2C分别为区段L2的三相母线。下文中同类符号的意义以此类推。

d)确定最小冲突集。将馈线终端单元(feeder terminal unit，FTU)上传的电压、电流故障状态信息代入到最小冲突集候选所对应的解析冗余关系中，计算出相对残差。若相对残差大于设置的门槛值，那么其所对应的最小冲突集候选就是最小冲突集。如图2中，若配电线路L2的A相和B相发生故障，则对应的解析冗余关系式(3)—(6)计算出的相对残差大于门槛值，于是从最小冲突集候选集{{L2A, B2A}，{L2B, B2B}，{L2C, B2C}}中确定出最小冲突集{{L2A, B2A}，{L2B, B2B}}。

e)计算最小碰集。本文采用文献[15]中的适应度函数，计算最小碰集

(9)

式中：ffitness(x)为粒子x的适应度值；NCx为最小冲突集C中的当前粒子x相交的冲突集合的数目；NC为在最小冲突集C中冲突集合的数量。

该适应度函数所对应的碰集判据为：

(10)

式中：CHS为碰集;Cnon-HS为非碰集。

利用上述得出最小冲突集{{L2A, B2A}，{L2B, B2B}}可以计算出最小碰集为：{{L2A,L2B}，{L2A,B2B}，{B2A,L2B}，{B2A,B2B}}。

f)确定故障元件。首先依据元件的先验故障概率值，采用贝叶斯方法计算出各个最小碰集的后验故障概率，并进行故障概率排序，选择故障概率值大的作为系统诊断结果，即判定为故障元件。

2 Petri网故障模式识别

2.1 配电网故障情况分析

配电线路的故障分为短路故障和断线故障2种。一般将配电线路A、B、C三相看作一个整体建立模型，下面分别对这2种故障类型进行分析。

2.1.1 短路故障

配电线路短路故障有相间短路和单相接地。如图3所示，IiA、IiB、IiC和IoA、IoB、IoC分别为配电线路输入侧和输出侧A、B、C三相电流；UiA、UiB、UiC和UoA、UoB、UoC分别为配电线路输入侧和输出侧A、B、C三相电压；Ag、Bg、Cg分别表示A、B、C单相接地故障；A-B、B-C、C-A分别表示相应两相短路故障；A-B-C表示三相短路故障。

图3 配电线路短路故障Fig.3 Short circuit fault of distribution line

单相接地故障时，如A相接地，故障边界条件为：

(11)

同理B相和C相接地的故障边界条件分别为：

(12)

(13)

式(11)—(13)中：ILA、ILB、ILC为配电线路上的A、B、C三相的最大负荷电流。

两相短路时，如发生A-B故障，故障边界条件为：

(14)

同理发生B-C故障和C-A故障时的相应故障边界条件为：

(15)

(16)

发生A-B-C故障时的边界条件为：

(17)

2.1.2 断线故障

根据电力系统断线的相关知识，A、B、C相均在断线故障下的边界条件为：

(18)

2.2 Petri网故障模式识别

2.2.1 基于Petri网的配电网故障模式识别模型

基于Petri网的故障模式识别，一般情况下，首先要建立Petri网故障模式识别模型。目前，Petri网络结构大部分用关联矩阵的形式来描述，一个典型的Petri网包含库所P，每一个库所用小圆来表示；变迁T，每个变迁用竖线来表示。依据上述配电网在不同故障类型下的故障信息，建立基于Petri网故障模式识别模型，如图4所示。图中共有23个位置(P1—P23)，10个变迁(T1—T10)。模型中库所代表的含义见表1。

图4 基于Petri网故障模式识别模型Fig.4 Recognition model for fault pattern based on based on Petri net

2.2.2 Petri网的矩阵描述

Petri网的结构和变迁点不仅可以用图形的方式来表示，还可以用矩阵的方法来实现。本文采用基于以下关联矩阵推理方法来实现[21]：

a)首先建立基于Petri网的故障模式识别模型。

表1 故障模式识别库所的含义Tab.1 Meaning of the fault pattern recognition library

b)根据MBD一致性理论判断出故障元件，利用故障特征量，确定初始托肯矩阵K1。

c)根据式(19)更新托肯状态Ki。

(19)

“⊕”的定义如下：

(20)

式中：X、Y、Z均为矩阵；m和k为矩阵Z的行列数；zij为Z中的元素，i=1,…,m,j=1,…,k；f为矩阵函数；f为变量函数，若f(zij)≥1，则f(zij)赋值“1”；若f(zij)=0,则f(zij)赋值为“0”。

“⊗”定义如下：

(21)

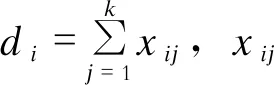
d)当Ki+1=Ki时，停止更新托肯状态，输出托肯状态。

根据配电线路故障信息、Petri网矩阵理论及图4故障模式识别模型，可得到输入关联矩阵D-和输出关联矩阵D+，即：

3 诊断流程

本文首先依据MBD一致性推理诊断出故障元件，再利用配电线路故障信息采用Petri网故障模式识别模型诊断出故障类型，具体诊断流程如图5所示。

图5 故障诊断流程Fig.5 Fault diagnosis flow chart

4 实例分析

图6为某10 kV单电源配电网子网，具有7个节点，每个节点都设置了相应的信息采集装置，该子网包含了10个信息测量点M1—M10。通过PSCAD软件建立相应的模型，进行仿真验证。

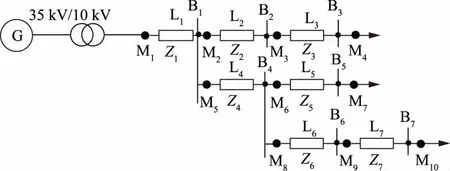
图6 某10 kV配电网子网Fig.6 A 10 kV distribution network subnet

4.1 MBD诊断过程

MBD诊断过程如下：

a)抽象系统元件。图6配电网中包含的系统元件有7个母线节点，用B1—B7表示，7条馈线区段，用L1—L7表示，其中，馈线区段的阻抗用Z1—Z7来表示。

b)建立解析冗余关系式。根据KCL和KVL定律，写出该子网的所有解析冗余关系式，具体结果见表2。

c)冲突识别。根据解析冗余关系所隐含的信息，离线地搜索出该系统的最小冲突集候选，其结果见表2。

表2 解析冗余关系式和最小冲突集候选Tab.2 Analytical redundancy relation and CMCS

d)确定最小冲突集。假设该子网中馈线L2的A相发生接地故障，馈线L7的C相发生断线故障，将电压和电流故障状态信息代入与最小冲突集候选相对应的解析冗余关系中，计算出相应的残差，具体结果见表3。

表3 各解析冗余关系的残差值Tab.3 Residuals of analytical redundancy relation

由于模型存在一定的误差，所以设置允许相对残差值为0.2，表2中所示相对残差大于0.2的最小冲突集为：CMCS={{L2A,B2A},{L7C,B7C}}。

e)计算最小碰集。本文采用文献[16]中BPSO算法求解最小碰集，其中采用适应度函数为F(X)=h/c，h表示当前粒子X与冲突集有交集的个数，c表示冲突集的总个数。BPSO具体相关参数设置如下： BPSO种群规模N=60，学习因子c1=c2=1.5,惯性权重w=0.9,最大迭代次数为T=100，种群空间维数D=21，通过仿真得出最小碰集为

CMHS={{L2A,L7C},{L2A,B7C},{B2A,L7C},{B2A,B7C}}。

f)确定故障元件。假设线路的故障概率为0.4，母线的故障概率为0.1，采用贝叶斯定理计算上述最小碰集的故障概率并进行排序，结果见表4。

表4 最小碰集故障概率排序Tab.4 Fault probability ranking of the minimum collision set

由表4可知，{L2A, L7C}的故障概率最大，因此，可以判断出线路L2和线路L7发生故障。

4.2 Petri网故障模式识别

上述基于MBD一致性推理方法诊断出故障元件，但是并没有诊断出故障类型，因此，需要通过Petri网进一步进行故障模式识别。根据检测到故障信息确定线路L2的初始托肯状态K1(L2)=[1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]，L7初始托肯K1(L7)=[0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0]；将初始托肯状态K1(L2)、K1(L7)带入式(20)更新初始托肯状态得到K2(L2)=[0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0]以及K2(L7)=[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0]；将K2(L2)、K2(L7)作为下一次迭代的初始托肯状态，再代入到式(20)中更新得到新的托肯状态K3(L2)=[0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0]以及K3(L7)=[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0]；对比2次值得出了K2(L2)=K3(L2)，K2(L7)=K3(L7)，迭代结束，于是判断出线路L2的A相发生接地故障，线路L7的C相发生断线故障。

5 结束语

本文提出了一种将MBD一致性推理与Petri网相融合的配电网故障诊断方法，具体如下：

a)基于MBD一致性推理，通过抽象系统元件， 建立解析冗余关系,离线地搜索出最小冲突集候选，采用BPSO智能算法计算最小碰集，判断出故障元件。

b)基于Petri网矩阵理论和配电线路在各种不同故障类型下的故障特征，建立故障模式识别模型，进一步判断出故障类型。

该方法融合了MBD一致性推理和Petri网的优点，建模清晰、直观。最后，以某10 kV配电网子网为例，验证了该方法不仅能快速、准确地诊断故障元件，而且能识别出故障类型。