基于固定检测周期的发电设备机会维修策略

李春梅，李冰，陈前明，胡迪，杨涛，张成，陈刚，杨嘉巍

(1.广东省粤电集团有限公司沙角C电厂，广东 东莞 523936；2.华中科技大学 能源与动力工程学院，湖北 武汉 430074)

近年来火电机组运行方式表现出调峰频繁、运行周期长的趋势，由之引起设备运行风险增加，设备出现故障隐患多、停机损失大、维修费用高、维修周期长等特点，这些对发电设备的可靠性提出了更为苛刻的要求[1-2]。同时，为了最大限度地实现电厂的经济效益，要求进一步合理安排发电设备维修周期与维修内容，从而降低维修成本。因此，为达到提高可靠性与减少维修费用的双向需求，电力行业正在寻找更准确和有效的发电设备维修策略[1-5]。

目前，在火力发电厂实际运行中采取的维修策略均主要是以时间为标准的计划维修和事后维修两种方式。计划维修是定期对发电机组各个设备进行维护检修，主要是根据过去的运行数据和情况确定检测周期，维修周期一般是1～2 a，但由于不同设备的故障率不同，可能造成某些设备过修或维修不足。事后维修是当部件或设备出现故障后进行维修，维修成本完全取决于在运行周期内设备的故障次数，该维修方式具有很大的随机性[4]。

近年来，国内外学者将状态维修策略用于到发电设备的检修中，以减少其运营维修费用，提高发电设备可靠性[6-10]。然而，火电机组作为一种由多设备组成的复杂系统，针对单一设备的优化维修研究是远远不够的，考虑设备之间维修相关性的机会维修策略成为研究重点。对于火电机组，重要设备的故障维修必然伴随着巨大的停机损失，机会维修策略就是利用机组的停机时间，对机组其他满足预设条件的设备进行提前维修，从而达到节省维修成本的目的[11]。机会维修策略可以分析与每个维修任务相关的成本与收益，同时优化连续维修任务之间的时间间隔，更适用于电力系统运维。同时，考虑系统多状态时，设备间的关联更加复杂，如何在检修决策中进行统筹，是机会维修理论的研究热点[12]。Qi等人[13]考虑定期维修和机会维修，研究了多组分系统的最优维修策略；Zhu等人[14]研究了具有两个独立故障模式的多分量系统的机会维修建模；Zhang等人[15]建立了一种基于条件的多单元系统联合机会预防性维修和备件供应策略，对每个维修决策点分析可能的维修需求及其相应的维修概率；Zeng等人[16]则提出一种基于动态条件的多组件系统机会维修策略，在考虑经济和随机依赖的同时，实时预测剩余使用寿命；徐波等人[17]融入设备随机故障情景，建立基于机会维修的系统状态检修决策数学模型。上述研究多是将运行时间作为维修阈值，维修决策的制订仅在系统故障停机时进行。此外，少有文献考虑基于系统的整个运行生命周期的维修策略优化，即使部分文献考虑了全寿命，但未考虑设备间的多种相关性。部件之间的维修相关性一般归纳为3类：经济相关性、故障相关性和结构相关性。经济相关性是指多个相关部件一起维修时比单独维修的费用更低；故障相关性是指整个系统不同部件间的故障相互作用、相互联系；结构相关性是指由于结构的约束，对某一部件维修的同时必须对其他相关部件进行维修。由于这些相关性的存在，在对系统中的某一部件做维修决策时，就需要考虑它与其他部件之间的相互影响[18]。

因此，为了丰富维修措施的选择并充分利用系统停机时间，本文提出基于固定检测周期的发电设备机会维修策略，考虑多种维修方式和维修组合在系统整个运行生命周期中对维修结果的影响，在维修计划中引入一个固定的检测周期，进行实时可靠性评估，以预测设备的恶化趋势，帮助维修人员做出维修决策。研究中不考虑故障相关性，只考虑维修资源以及部件结构的关联，当对一个部件进行维修时，考虑对其他相关部件进行维修的机会，以节省时间、资源、人力等，从而节省维修成本。

1 模型假设及基本理论

1.1 模型假设

本文的机会维修模型假设系统包含4个子设备，建立它们之间基于固定检测周期的机会维修模型，并进行以下假设：

a)各设备的故障率相互独立，且服从两参数威布尔分布；

b)设备的维修方式包括事后维修、不完全维修、预防性更换维修和机会维修；

c)设备i的维修成本由事后维修成本Ci,f、不完全维修成本Ci,m、预防性更换维修成本Ci,p、和机会维修成本Ci,o组成；

d)与机组整体运行时间相比，可忽略设备维修和状态检修时间。

1.2 可靠性理论

设备的可靠性是指在特定的时间和环境下完成规定功能的能力，可用一系列从1到0变化的函数来描述，表征设备状态从正常到故障的变化过程。对发电设备的故障统计数据研究表明，两参数威布尔分布可以近似表达出其可靠度的变化过程。设备i的可靠度函数可以表示为

(1)

式中：αi为设备i尺度参数，αi值影响威布尔函数曲线尺寸比例的大小；t为时间；βi为设备i形状参数，βi值影响曲线的形状。

设备失效率表示产品劣化过程中丧失工作能力的概率，对于满足两参数威布尔分布的设备i而言，其失效率函数可表示为

(2)

1.3 机会维修策略

机会维修策略利用系统停机时间，对状态不好但尚能运行的设备进行维修。在传统的预防性维修的基础上考虑设备维修之间的相关性，利用系统中某一设备发生随机故障或达到预防维修阈值导致的系统停机时间，对系统中其余尚未故障的设备进行一次维修，可以考虑将未发生故障的设备维修时间提前，从而在系统全寿命运行周期内降低巨大停机损失，以达到节约成本的目的。基于可靠度R的机会维修策略如图1所示，其中Rp、Ro分别为预设预防性维修阈值和预设机会维修阈值，tp、to分别为预防性维修时刻和机会维修时刻。

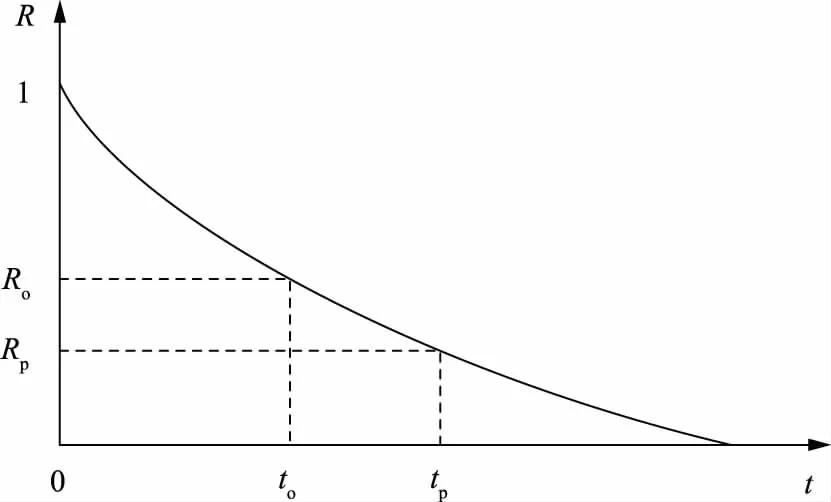
图1 机会维修策略Fig.1 Opportunistic maintenance strategy

基于设备可靠性理论，预先设定系统各设备的预防性维修阈值和机会维修阈值，当设备运行在0～to时间段，发生随机故障时，系统即停机进行更换维修；当设备运行在to～tp时间段，发生随机故障即停机更换，或其他设备故障导致系统停机时进行机会维修；当设备运行至tp时刻，进行预防性更换维修。

2 机会维修策略模型

2.1 维修判断过程

维修判断过程流程如图2所示。

图2 维修判断流程Fig.2 Maintenance judgment process

现有维修策略大多将设备预防性维修周期或随机故障作为维修依据，而不考虑设备的状态信息或维修计划。在实际火力发电厂的运维计划中，当设备发生随机故障时，采取事后维修措施来及时更换设备；当设备运行时间达到预设维修阈值时，采取预防性维修进行预防性更换维修。本文在维修判断过程中增加一个固定检测周期(如图2所示。)

在对设备进行状态监测时，如果设备实时可靠性小于其维修阈值，则认为设备的劣化程度已非常严重，将采取更换措施进行维修，否则，进行不完全维修以改善部件运行状况。已有相关文献对实时可靠性评估进行了研究，以获取组件的实时状态信息，为维修计划提供指导[6-12]。

在以下讨论中假设事后维修、预防性维修和机会维修将设备恢复到全新状态，而不完全维修将设备恢复到故障之前的某一状态，但是具有更快的劣化速率。混合故障率模型能有效描述不完全维修对部件失效率的影响，模型表示为

hk+1(t)=bhk(t+aTk)，

t∈[0,Tk+1],k=1,2，… .

(3)

式中：a为役龄递减因子；b为故障率递增因子；Tk为第k次维修周期的时间长度。

2.2 基于固定检测周期的机会维修策略

图3所示为机会维修策略仿真流程。图3中：tf、tp、ts、to分别为设备的故障维修时刻、预防性维修时刻、固定检测周期和机会维修时刻；ti,f、ti,p、ti,s、ti,o分别为设备i的故障障维修时刻、预防性维修时刻、固定检测周期和机会维修时刻(下标j表示设备j)；Ri、Ri,p、Ri,m、Ri,o分别为设备i的可靠度阈值、预防维修可靠度阈值、不完全维修可靠度阈值和机会维修可靠度阈值；fi,f、fi,p、fi,m、fi,o分别为设备i的故障维修频次、预防性维修频次、不完全维修频次和机会维修频次。仿真过程如下所述。

图3 机会维修策略仿真流程Fig.3 Simulation process of opportunistic maintenance strategy

步骤1，初始化仿真并定义模型中所包含设备的相关数据信息，包括：不同设备威布尔分布参数α和β、役龄递减因子a和故障率递增因子b、设备固定检测周期ts、预防性维修阈值Rp、系统总的仿真时间Ttotal、系统停机维修时间Tk、每个设备维修频次(事后维修、预防性维修和不完全维修，初始值为0)。

步骤2，重新生成每个设备的随机故障维修时刻tf、预防性维修时刻tp以及固定检测周期ts。对可靠性函数进行随机抽样，得到随机故障维修时刻；根据设备的可靠性函数和预设预防性维修阈值求解预防性维修时刻，根据维修计划设定固定检测周期。

步骤3，获取系统的维修时刻tk和响应的维修设备i。系统维修时刻为随机故障维修时刻、预防性维修时刻和固定检测周期的最小值。

步骤4，维修决策。当系统中任何设备发生随机性故障时，必须进行事后维修，并更新故障维修频次ff；当系统中任何设备可靠性达到预防性维修阈值时，采取预防性维修，并更新预防性维修频次fp；当系统中某一设备到达了固定检测周期时，维修人员应获取设备的运行信息，如果设备实时可靠性低于预设的预防性维修阈值时，则认为该设备状态劣化比较严重，应采取预防性更换维修，否则采取不完全维修来改善设备运行状态；最后，为系统中每个设备重新生成和更新随机故障维修时刻、预防性维修时刻和固定检测周期。

步骤5，机会维修策略。根据不同设备预设的机会维修可靠度阈值Ro，利用威布尔分布可靠度函数求解对应的机会维修时刻to。当系统中有设备进行事后维修或预防性更换维修导致系统停机时，系统中可靠度低于机会维修阈值的设备借此机会进行机会维修，并更新机会维修频次fo和未进行机会维修设备的故障维修时刻、预防性维修时刻、固定检测周期和机会维修时刻。

步骤6，更新系统中各设备维修频次和仿真运行时间。

步骤7，如果系统仿真时间未达到运行周期，则返回步骤2；否则输出系统中各设备维修频次。

2.3 设备维修成本定义

将系统各设备项维修措施的维修频次与相应维修成本相乘后取和，用来表示设备在整个运行周期的维修成本，具体表示为

(4)

式中Ci为设备i在系统运行周期内总的维修成本。

3 算例分析

火电机组系统庞大且复杂，本文为了展示基于固定监测周期的发电设备机会维修策略的优越性，假设系统包含4个子设备来简化表示整个机组系统，系统各设备的初始仿真参数设定见表1。

表1 仿真参数Tab.1 Simulation parameters

每个设备的预防性维修可靠性阈值Rp和固定检测周期ts总是按照维修计划和运行环境预先提供。为了简化仿真过程，除α和β外，其他参数对于不同设备均设置为相同；系统的运行周期设为30 a，记录下每次仿真过程的各设备各种维修方式的维修频次；分析计算预设的总仿真次数为1 000次，每次仿真系统均产生新的随机数，可认为这1 000次仿真相互独立，仿真结果的均值能近似表示维修策略的仿真结果。

3.1 基于固定检测周期的维修策略仿真结果

在传统预防性维修基础上设定固定检修周期，在不考虑机会维修策略的情况下，研究设备不完全维修可靠度阈值Rm对各种维修方式频次的影响，仿真结果如图4—5所示。

本文以子设备1为例，在传统的预防性维修策略下，事后维修平均次数为0.819次，预防性更换维修平均次数为7.446次，假设其维修成本满足Ci,f∶Ci,p∶Ci,m=10∶5∶1，传统预防性维修策略下的总维修成本为45.42单位成本。图6为总维修成本随不完全维修可靠度阈值的变化趋势。

从图4—5可以看出，随着不完全维修可靠度阈值从0.91增加到0.99，故障维修频次和不完全维修频次逐渐下降，而预防性维修频次则呈现相反的趋势；这说明随着不完全维修可靠度阈值的增加，维修行为倾向于设备更换，从而导致预防性维修频次增加，事后维修频次和不完全维修频次降低。基于固定检测周期的维修策略的故障维修频次和预防维修频次明显低于传统的维修策略。从仿真结果可知，固定检测周期的引入有助于检修获取各部件的运行状态信息，以便积极采取改进措施，降低随机故障的发生。

图4 事后维修频次和预防性维修频次分别与不完全维修阈值的关系Fig.4 Relation between corrective maintenance frequency and imperfect maintenance threshold，preventive maintenance frequency and imperfect maintenance threshold

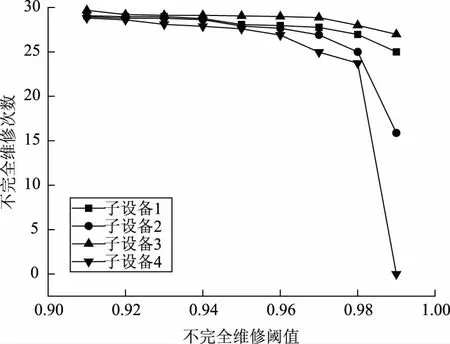
图5 不完全维修频次与不完全维修阈值的关系Fig.5 Relation between imperfect maintenance frequency and imperfect maintenance threshold

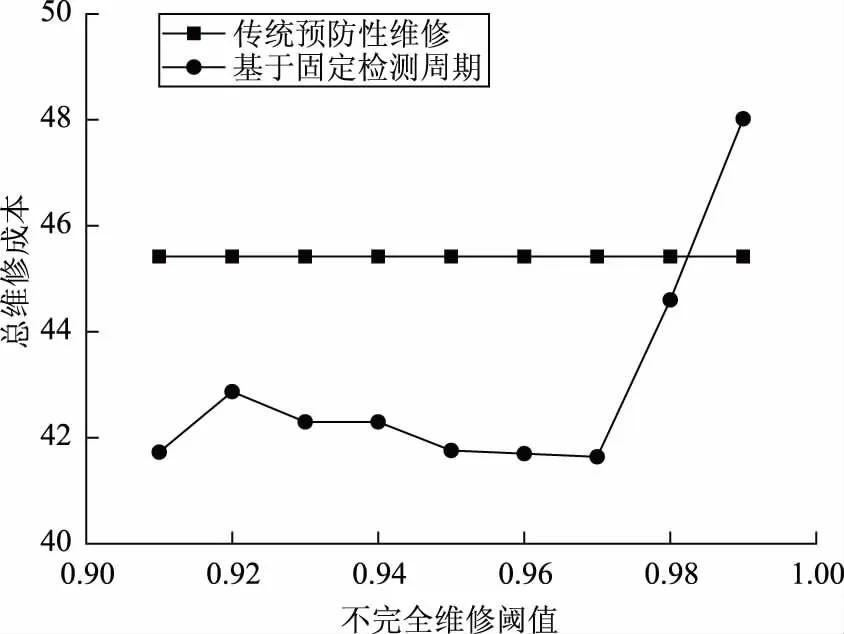
图6 总维修成本与不完全维修阈值的关系Fig.6 Relation between total maintenance cost and imperfect maintenance threshold

从图6可以看出，仿真模型中子设备1在不完全维修阈值设定为0.97时，总的维修成本最低为41.67单位成本，较传统预防维修策略降低了8%的费用。一般情况下，不同维修成本比对应于不同的最优不完全维修可靠度阈值，仿真模型参数可根据不同的维修实例进行调整，从而为火电厂设备的实际运行维修提供指导意见。

3.2 考虑机会维修策略仿真结果

一般来说，机会维修可靠度阈值Ro应该大于预防性维修可靠度阈值Rp。考虑机会维修策略时，为体现本文所提出的机会维修策略模型的优势，将其与文献[19]提出的机会性替代维修策略进行比较。以子设备1为例，所设预防性维修可靠度阈值Rp为0.9，机会维修可靠度阈值Ro为0.91，不完全维修可靠度阈值Rm为0.95，系统运行周期为30 a。表2列出了两种策略以及仅考虑预防性维修和事后维修的传统维修策略的仿真结果。

从表2可看出，与仅考虑机会维修策略相比，本文所提策略考虑了不同维修方式的组合，故障维修频次和预防维修频次更低，效果更好。

表2 仿真结果对比Tab.2 Comparison of simulation results

4 结束语

考虑不完全维修和多种维修方式相组合的机会维修策略在火电领域越来越受关注，现有文献主要将运行时间视为维修阈值，并且仅在系统停机时才做出维修决策。但是，系统的实际运行状态与运行时间并不是线性关系，应该根据设备的实时运行状态进行维修决策。

本文提出一种基于固定检测周期的发电设备组合机会维修策略，在维修策略中引入固定的检测周期，进行实时可靠性评估，以此预测设备的恶化趋势。结合具体算例，在考虑维修成本的同时，研究了不同维修策略在整个运行生命周期中对维修结果的影响，提出维修方式的最佳组合，可为火电站实际运维管理和检修决策提供更科学有效的指导。本文算例中的不同维修成本比对应不同的不完全维修可靠性阈值，模型参数可以根据不同的维修实例进行调整；后续研究可根据应用效果，考虑不同仿真参数设定值对策略的影响，修正模型参数，从而做出更准确的运行与维修决策。对于实际维修中存在的设备数量以及其他维修相关性等问题也有待考虑到模型中，开展更加深入的研究。