基于可拓学与仿生学的板壳结构设计

(济南大学 机械工程学院，山东 济南 250022)

板壳结构以其轻量化、承载能力强和易于加工的特点而广泛应用于航空航天、汽车工业、轮船制造等领域[1]。为了实现轻量化和强承载能力，一种典型的设计是在基板上布置加强筋，在实现轻量化的同时，也能保证具有足够的承载能力。传统的加强筋多为米字型、井字型等简单设计[2]。随着拓扑优化理论的不断完善[3-4]，许多学者将变密度、均匀化和渐进结构应用到板壳结构设计中[5-6]。由于离散拓扑优化理论可适用算例较少，而且优化结果极易出现棋盘格式、网状格式等传统布局格式，因此应用范围十分有限。

随着近年来仿生学的发展，一些学者开始将仿生学应用于板壳结构的设计。仿生学的运用为板壳结构的优化设计提供了新的设计思路。丁晓红等[7-8]、季学荣等[9]根据植物根系的生长机理，提出一种自适应成长算法设计，用于板壳结构加强筋布局设计。植物根系总能根据自身所处环境自适应成长而使整体功能达到最优，将该特点运用到板壳结构的优化设计中，提高了优化设计的效率。薛开等[10]根据双子叶植物叶脉脉序生长规律，提出一种适用于板壳结构加强筋布局设计的仿生脉序生长算法。根据该算法得到的加强筋板材易于加工，增强效果明显。目前，仿生板壳结构设计领域的研究主要集中在仿植物根系或者叶脉脉序，对飞行昆虫的研究较少。蜻蜓、蝉等飞行昆虫的翅膀质量仅占体质量的1%～2%，但是能够保证飞行过程中极高的稳定性和承载能力。本文中以蝉翼为仿生对象，通过将可拓学与仿生学相结合，分析蝉翼的构成及机理，探讨各组织结构对承载能力的贡献度，利用各结构贡献度的大小对板壳结构进行仿生设计，利用有限元软件对仿生模型和传统模型进行仿真分析。

1 仿生可拓模型构建

1.1 仿生学与可拓学

仿生学是利用在生物界发现的机理和规律来解决人类需求的综合性交叉学科[11]。它将生物经过亿万年进化逐渐具有的各种与生存环境高度适应的功能特性移植到相应的工程技术领域中，为人类提供灵活、高效的技术系统[12]。目前，仿生领域以单元仿生为主，例如材料仿生、形态仿生、结构仿生、构型仿生等。近几年，随着仿生学的发展，单元仿生向多元仿生发展成为新的趋势。多元耦合仿生是仿生学的最新发展成果，其中生物耦元是指对生物功能实现有贡献的各种因素，是构成生物耦合的基本单元[13-14]；生物耦合是指2个或2个以上耦元通过一定的方式组合在一起，成为一个系统或生物实体。多元耦合仿生可以解决部分传统单元仿生难以解决的问题。

可拓学是一门涵盖哲学、数学和工程学的交叉学科，由蔡文[15]于1983年首先提出。可拓学的核心是基元理论、可拓集理论和可拓逻辑。近年来，可拓学研究者把可拓论和可拓创新方法与其他领域相关知识交叉融合产生了可拓工程，例如与信息科学交叉融合，以物元、事元和关系元表示信息建立信息和知识的形式化模型，通过可拓变换和可拓推理建立了解决问题的模型[16-17]。洪筠等[18]将可拓论与生物耦合相结合，提出生物耦合可拓分析法，对生物耦合与生物模本进行分析。对于多元耦合生物模本的可拓研究有助于分析其耦合机理，通过生物模本的软、硬分析可揭示生物的系统组成和内外关系。

1.2 优选多元耦合仿生模本

生物模本是仿生学的基础，如果没有生物模本，则仿生即为无本之木、无源之水。仿生模本的优选直接关系到仿生设计的成败，因此在仿生设计时，生物模本必须优选。在优选过程中首先要对目标需求进行需求分析，然后寻找与其有相似性的仿生模本。

1.3 生物耦元的确定与可拓模型构建

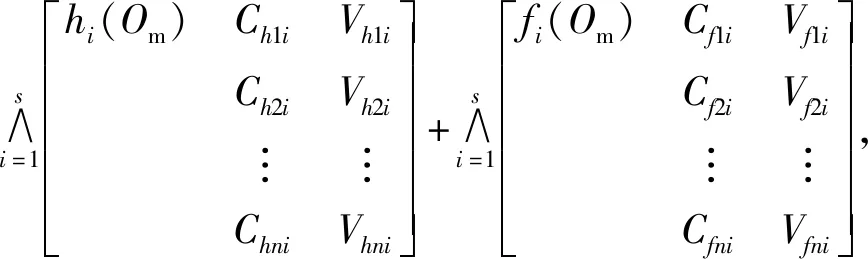
式中：Ch为生物硬部特征；Vh为生物硬部特征所对应的量值；h(Om)为生物硬部，由n个特征Ch1,Ch2,…,Chn，以及所对应的n个量值Vh1,Vh2,…,Vhn组成的阵列构成；Cf为生物软部特征；Vf为生物软部特征所对应的量值；f(Om)为生物软部，由n个特征Cf1,Cf2,…,Cfn，以及所对应的n个量值Vf1,Vf2,…,Vfn组成的阵列构成。

同理，根据潜、显分析结果，潜部用t(Om)表示，显部用p(Om)表示，则Om=t(Om)+p(Om)。依据可拓共轭理论建立生物可拓模型的步骤见图1。

图1 可拓分析模型

1.4 判断矩阵构造与生物耦元贡献度计算

生物各组织结构对于生物功能实现的贡献度是不同的。精确计算各生物结构对生物功能实现的贡献度可使工程仿生的目标更加明确，从而提高仿生设计的效率。层次分析法有较严格的数学依据，广泛应用于多层次、多指标复杂系统的分析与决策，非常适合生物耦元重要度的分析。基于试验优化的层次分析法的基本思路如下：1)选定生物模本，用符号表示生物系统结构集合X={x1,x2,…,xn}，n为生物系统耦元的总个数。2)根据生物耦元分析表列出判断矩阵A，其中的元素xij为生物系统耦元xi相对于生物系统耦元xj的重要程度(i、j为生物系统耦元顺序，1≤i≤n,1≤j≤n)，其取值为标度，如表1所示。矩阵A中xji的取值为xij的倒数，即xji=1/xij。求解矩阵A的最大特征根及所对应的特征向量，经归一化处理后，得出各生物结构对功能实现的贡献度。3)通过计算判断矩阵的一致性检验，得出每个生物结构的贡献度。一致性检验公式为

(1)

(2)

式中：E为矩阵A的一致性检验指标；λmax为矩阵A的最大特征根；r为随机一致性比例；I为矩阵A的随机平均一致性检验指标。当n为0、1、2、3、4、5时，I取值为0、0、0.58、0.90、1.12、1.24。

表1 判断矩阵标度及其含义

用一致性比例r的取值来检验一致性，当r=0时，判断完全一致；r>0,且r<0.1时，A具有满意的一致性，否则需要调整判断矩阵A。

2 蝉翼仿生可拓模型构建

2.1 板壳结构仿生模本优选

蝉又名知了，是飞行昆虫中较大型的昆虫[20]。其翅膀的质量仅占自身体质量的1%～2%，但是蝉在飞行过程中能表现出极高的稳定性和承载能力。将蝉翼质量与身体按比例扩大，是相同质量飞机机翼承载能力的10倍以上。板壳结构既需要轻量化又需要强大的承载能力，该主要功能需求与蝉翼承载功能有很大的相似性，因此将蝉翼作为仿生模本。

蝉翼主要由不同尺寸的翅脉和一定刚度的翅膜组成。蝉的翅脉通常分为前翅脉、后翅脉、中间支脉、加固尾脉4个部分，如图2所示，其尺寸如表2所示，其中部分数据引自文献[21]。蝉翼的翅脉为整个蝉翼提供了主要的支撑结构。

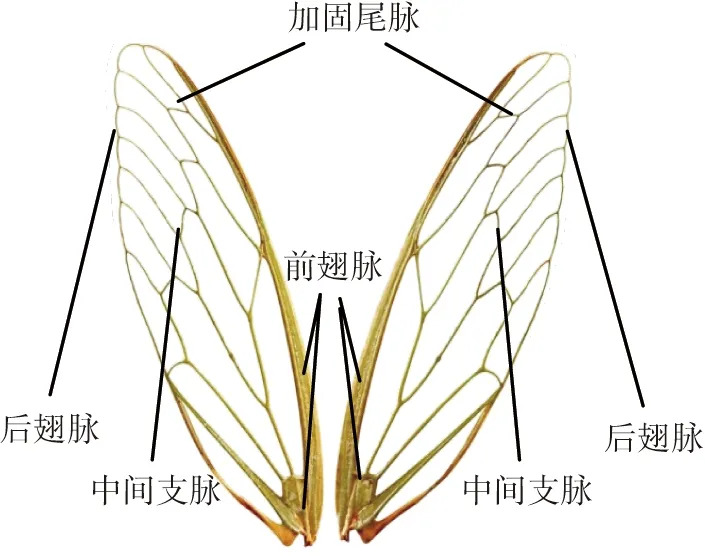
图2 蝉翼示意图

表2 蝉翼翅脉结构数据

翅膜主要由表皮和表面蜡质材料构成。表皮由一层网格状的纤维构成，可以使翅室在各个方向同时抵抗载荷，同时也可以提高临近单元的翅脉的抗弯曲性和扭曲度。表皮材料主要由几丁质(蛋白质和脂类化合物)和基质构成。在近翅端，翅膜厚度约为0.12 mm，在远翅端翅膜厚度约为0.04 mm，材料密度为1 mg/mm3。

2.2 蝉翼仿生多元耦合可拓模型构建

对蝉翼进行机理分析可知，蝉翼承载功能的实现是由翅膜形态、翅脉结构分布以及纤维组织和几丁质材料共同作用的结果，因此确定蝉翼生物耦合的耦元为翅膜形态耦元、翅脉结构耦元、纤维组织和几丁质等材料耦元。根据对蝉翼结构的描述，构筑蝉翼结构的可拓模型为

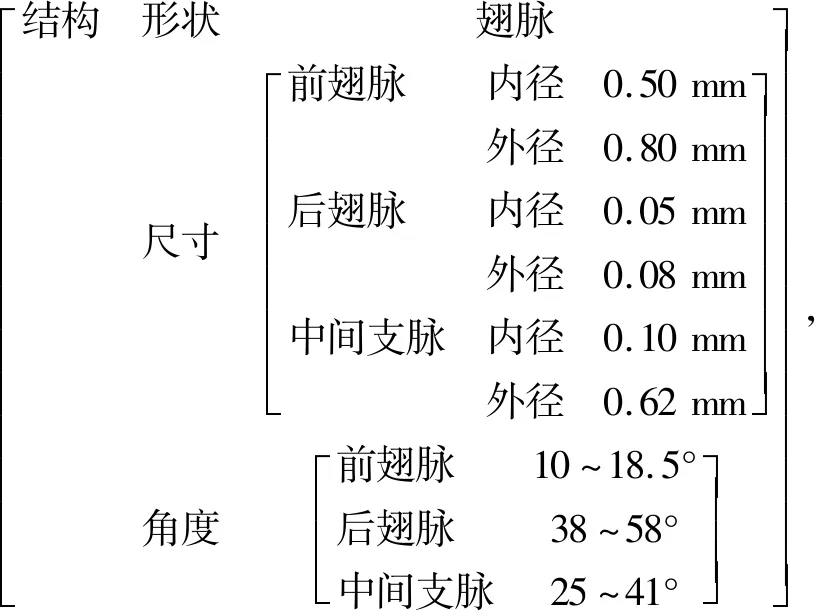
式中：Mi，Mj分别为第i、j个耦元(i,j=1,2,3)；R为耦联方式；Cr为关系的特征；Vr为关系特征相对应的量值；Vr3=[紧密，较紧密]；Vr4=[组合，嵌合，复合]；Vr5=[叠加，阶梯]；Vr6=[永久]。

式中Vm1=[降低，支配对象，自身重量]∧[增强，支配对象，承载能力]。

2.3 判断矩阵构建与主耦元确定

根据蝉翼可拓模型，用x1、x2、x3表示翅脉结构耦元、翅膜形态耦元、材料耦元。根据层次分析法列出判断矩阵A，即

(3)

将判断矩阵A代入AG=λmaxG，得到特征向量为G=(0.928 1,0.328 8,0.174 7)，最大特征根λmax=3.003 7，代入式(1)、(2)得一致性检验结果为

(4)

(5)

根据计算数据分析，结果符合一致性检验结果要求，因此，在蝉翼承载能力功能生物耦元中，翅脉结构耦元、翅膜形态耦元和材料耦元的贡献度分别为0.412 1、0.184 7、0.086 9。蝉在飞行过程中翅膀的承载能力的实现主要依靠翅脉结构耦元，其次为翅膜形态耦元和材料耦元。

3 仿生设计

3.1 仿生模型构建

由于蝉翼翅脉结构、翅膜形态、材料组成特别复杂，因此不能完全复制蝉翼，否则既不现实，也不经济。根据式(3)的计算结果，选择蝉翼承载功能的主耦元即蝉翼翅脉结构耦元作为仿生模本，蝉翼翅脉结构耦元中翅脉的分布特点对承载能力起决定性的作用，因此是仿生设计的主要依据。

根据2节中对蝉翼翅脉结构的分析，根据蝉翼翅脉分布规律，在尺寸为1 000 mm×1 000 mm×5 mm(长度×宽度×高度)的基板上布置加强筋。为了便于加工，筋板的尺寸统一设为10 mm×2 mm(高度×厚度)。筋板根据蝉翼翅脉分布结构分为主脉和次脉，主脉之间的角度取蝉翼主翅脉之间角度的平均值17°，模仿蝉翼后翅脉之间的角度，次脉之间的角度取为30°～40°，所有圆角半径均为10 mm，如图3(a)所示。作为对比，建立传统型板壳结构，基板尺寸为1 000 mm×1 000 mm×5 mm(长度×宽度×高度)，筋板尺寸为10 mm×2 mm(高度×厚度)，筋板分布为传统网格状，网格尺寸为60 mm×60 mm(长度×宽度)，所有圆角半径均为10 mm，如图3(b)所示。

(a)仿生型

(b)传统型图3 仿生型与传统型板壳结构

3.2 模型仿真与分析

在相同的载荷和边界条件下分别对传统型板壳结构和仿生型板壳结构进行静力学有限元分析。材料选为结构钢，属性如下：弹性模量E为210 GPa，屈服力σs为275 MPa,密度为7 800 kg/mm3，泊松比为0.28，在板壳结构上平面加载10 000 N的均匀载荷，图4所示分别为传统型和仿生型板壳结构的应力与变形分布。

表3所示为传统型和仿生型板壳结构有限元分析结果。从表中可以看出，与传统井字型板壳结构相比较，仿生型板壳结构质量减小了5.06%。在压力10 000 N的作用下，由图4(a)可知，仿生型板壳结构最大应力主要分布在主筋板和次级筋板中，最大值为140.79 MPa。由图4(b)可知，传统的板壳结构最大应力主要分布在对称的基板板中，最大值为163.08 MPa。与传统型板壳结构相比，仿生型板壳结构最大应力减小15.83%。由图4(c)、(d)可知，仿生型和传统型板壳结构最大变形均在中心位置，变形量分别为1.95、2.04 mm。与传统型板壳结构相比，仿生型板壳结构最大变形量减小了4.62%，表明仿生设计更合理，能有效地使应力均匀分散。由此可见，相对于传统的井字型板壳结构，仿蝉翼结构设计的板壳结构在实现轻量化的同时，还能有效地改善板壳结构的力学性能，应力区域分布更均匀、合理，是一种比较理想的板壳结构设计方案。

(a)仿生型板壳结构应力分布

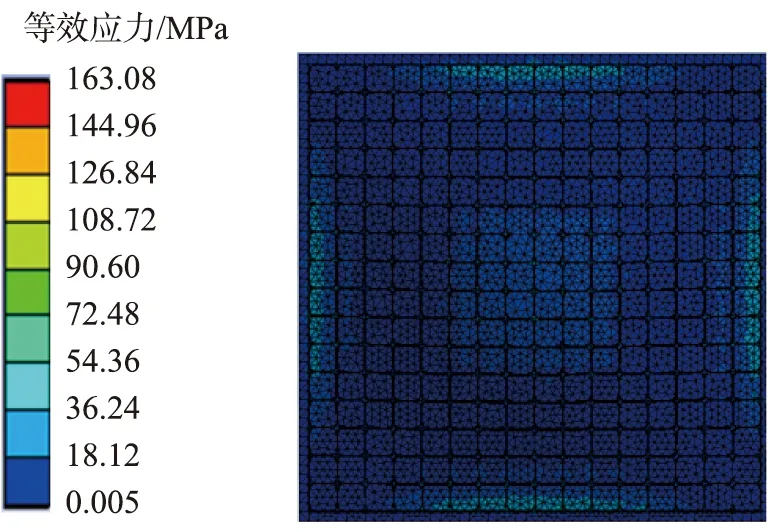
(b)传统型板壳结构应力分布

(c)仿生型板壳结构变形分布

(d)传统型板壳结构变形分布图4 仿真分析结果

表3 传统型和仿生型板壳结构有限元分析结果

4 结语

本文中将可拓学的基元理论、共轭理论和仿生学相结合，建立了生物耦合可拓模型，形成了对仿生模本定性与定量分析的有效工具，从而使非生物学设计者也能清晰地了解生物结构。

1)运用层次分析法，通过构建判断矩阵计算各生物各耦元的贡献度。生物耦元贡献度的确立可以进一步明确仿生目标，有助于提高仿生设计的效率。

2)通过借鉴蝉翼的结构规律对板壳结构进行仿生设计得到仿生型板壳结构。运用仿真软件进行静力学分析，相对于传统的板壳结构质量减小了5.06%，应力减小了15.83%，有效地提高了板壳结构的承载能力。