基于自适应分数阶傅里叶变换的地质雷达直达波抑制方法

周丽军

（山西省交通科技研发有限公司，山西 太原 030032）

0 引言

直达波抑制问题最早出现在探地雷达应用中[1]，当探地雷达在检测被掩埋目标时，根据接收到的目标反射信号特点判断被掩埋目标，发射信号从空气中入射到掩埋目标时在地面会产生较强的反射信号，这种反射信号将叠加在目标反射信号中形成直达波信号，由于直达波信息强度大，对目标信号检测造成干扰，因此在提取目标反射信号前需要去除直达波。针对直达波抑制问题，目前常用的有背景相消法、平均对消法、门限法、收发隔离法等[2-4]，利用平均对消法在去除直达波信号的同时，也去除了一部分目标的反射信号，若反射信号较弱则难以保留有效信息。应用背景相消法需提前采集没有目标的背景直达波信号，再采集有目标的回波信号，从接收回波中减去背景直达波，但考虑到实际环境的不同，在应用中采集背景直达波信号比较困难。还有文献则根据信号在时间、空间上的不同特征，提出时域滤波、空域滤波、时- 空域滤波相结合的方法抑制直达波[5]。还有学者利用目标与环境在空间与频域上的差异，采用距离- 方位- 多普勒三域联合处理方法抑制直达波[6]。

自适应技术在抑制直达波中应用也很广泛[7-8]，其思想是利用直达波信号与反射信号相关性很低的特征来分离直达波，如有文献提出利用两道相邻波形中直达波的相关性进行自适应对消滤除直达波，但是考虑到接收的直达波信号若受到信道噪声污染或有较多干扰源，抑制效果将不理想[9]。还有文献建立了稀疏模型，使用其形态成分分析技术重构有效目标信号与干扰信息[10]。有文献提出基于经验模态分解（EMD）或者集成经验模态分解（EEMD）模型的方法，将信号分成多个单频信号和残余信号，从中分离出直达波，此方法适合不平稳信号的处理[11-12]。

分数阶傅里叶变换是将信号映射到时频域空间，实现信号时频域展开，同时不同阶次分数阶傅里叶变换对应不同的时频域，展示出信号从时域逐步变化到频域的所有变化特征，可以为信号的时频分析提供更大的选择余地[13]。有文献利用分数阶傅里叶变换进行动目标检测与识别，通过选择合适的变换阶数，将最佳分数阶傅里叶变换域的信号幅值作为检测统计量，与门限进行比较后判断目标有无[14]。有文献在分数阶傅里叶变换域进行滤波从而抑制噪声域干扰[15]。由于变换角度的可变性，使得信号在不同分数阶傅里叶变换中存在多种结果，因此需要寻求一个最优的变换角度，使得变换结果最能体现需求。目前解决这一问题的思想主要集中于最小时间带宽积原理、最大幅值原理、最大峰度系数原理等[13]。

本文提出基于自适应分数阶傅里叶变换的地质雷达直达波抑制方法，根据直达波与目标回波曲线形状的差异将其映射到分数域空间，逐步调整分数阶实现直达波与目标信息在分数域的分离，并建立目标区域与直达波区域能量比最大化的准则，获取最佳分数阶的直达波抑制效果。

1 分数阶傅里叶变换

一维信号x(t)的p 阶分数傅里叶变换定义为[13]：

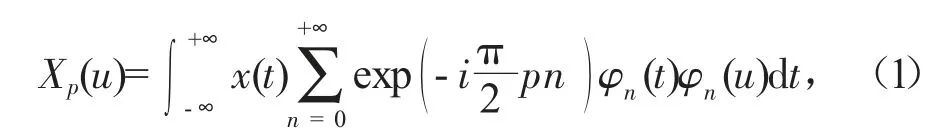
式中：exp （-iπpn/ ）2 是分数阶傅里叶变换的特征值；φn(t)是归一化的Hermite-Gaussian 函数。由一维分数阶傅里叶变换的定义，可以得到二维信号的分数阶傅里叶变换的定义为：

式中：Kp1,p2(s，t，u，v)=Kp1(s，u)Kp2(t，v)是可分离的变换核函数。

随着p1，p2的选择不同，可以利用多个阶次的分数傅里叶变换对信号进行多分数域分析。然而如何选择一个最佳的分数值，使得探地雷达回波的直达波在此分数域被抑制，而突出目标的信息，是接下来要解决的问题。

2 最佳分数阶选择

本文在抑制直达波的同时还需尽可能增强目标信号，因此可以考虑使用目标信号幅值能量与直达波幅值能量的比值作为最佳分数域的判定法则。那么对于信号 x(t,s)的（p1，p2）阶傅里叶变换 Xp1,p2（u，v），对其进行逆变换F-1{·}操作，能得到此分数域的图像为：

此时得到的图像为复图像，将上述复图像写成实部与虚部的形式：

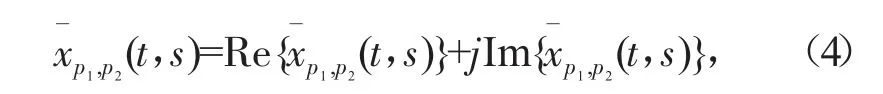
因此，其幅度部分就能写成：

对幅度信号进行测线方向累积，即：

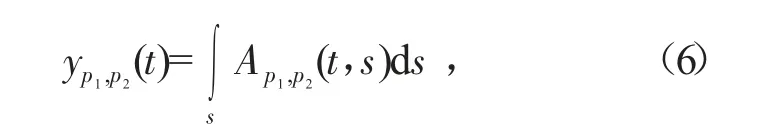
则yp1,p2(t)表示(p1,p2)阶分数域逆变换图像在时间上的能量值。对于选定的探地雷达天线，能估计出直达波的返回时间，设为t0，计算目标信号幅值能量与直达波幅值能量的比值，即：

3 实验结果与分析

利用长、宽、高分别为 1.8 m、1.2 m、0.6 m 的沙坑模拟地下环境，测得沙的相对介电常数为4.25，沙表面下方0.2 m 处埋入一水平放置的水瓶模拟充水病害，水管直径8 cm，长度20 cm。探地雷达为美国GSSI 公司的SIR-20 系列，天线中心频率为400 MHz，实验场景与目标放置位置如图1 所示。由于篇幅所限，本文取第10 道测线的数据进行处理。

第10 道测线的B 扫图如图2a 所示，在0～5 ns之间有较强的直达波，在6 ns 左右出现较弱的双曲线图像，由于400 MHz 天线分辨率较低，使得目标区域的回波与直达波部分重合。同时从图2a 中可以看出，在8 ns 附近有来自沙坑底部的回波以及电磁波在水瓶内的多次反射回波形成的干扰信号。

图2 第10道测线B扫图与分数阶傅里叶变换及其逆变换

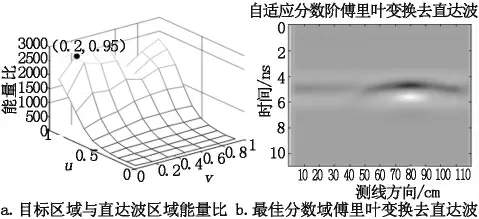
图3 最佳分数阶的选择与其傅里叶变换去直达波效果

图4 文献[11]与文献[12]去直达波方法

对测得的原始图像进行上述分数阶傅里叶变换，当取P1=0.6，P2=0.45 时得到的傅里叶变换如图2b 所示。在(0.6, 0.45)阶傅里叶变换中，呈现出3 个区域，分别映射了原始图像中的直达波、目标回波和沙底部背景回波。对此分数阶傅里叶变换进行逆变换，得到的逆变换图像如图2c 所示，比较图2c 与图2a，可以看出经过(0.6, 0.45)阶傅里叶变换逆变换得到的图像中，第一层直达波(1 ns 附近)幅值能量降低，而目标区域的幅值能量有明显的提升。对图2c的图像继续做分数阶傅里叶变换以及逆变换，式（7）的能量比值，对分数阶P1与P2遍历[0 1]区间值，取能量比值最大的分数阶为最佳分数阶傅里叶变换，如图3a 所示，在(0.2, 0.95)阶时获得最大能量比，由此得到的自适应分数阶傅里叶变换的逆变换图如图3b 所示，比较图3b 与图2a，能明显看出直达波已被去除，同时也去除了沙底反射的背景回波，而且增强了目标区域能量。

将本文方法与平均对消法[11]、EMD 去除直达波方法[2]进行比较，如图4 所示，利用平均对消法去除了0～4 ns 处的直达波，但同时也减弱了目标区域能量，并且增强了电磁波在目标内的多次反射回波。利用EMD 方法增强了目标区域能量，去除了直达波，但也增强了电磁波在目标内的多次反射回波。而本文方法则有效去除了多次反射回波，进一步增强了目标区域能量。

4 结论

本文提出基于自适应分数阶傅里叶变换的地质雷达直达波抑制方法，将探地雷达接收回波中的水平线状直达波与双曲线状目标回波映射到分数域空间，进行分数阶傅里叶变换，实现信号在分数域的时频展开，通过多次变换逐步分离直达波与目标信息。建立重构图像中的目标区域与直达波区域能量比最大化的准则，获取最佳分数阶的直达波抑制效果。在最佳分数阶傅里叶变换处理下，既抑制了直达波，同时也增强了目标回波。相比于平均对消法与EMD方法，本文提出的方法除了抑制直达波，增强目标回波，还能有效去除多次反射产生的干扰。