桥梁健康监测中车辆荷载应变的实时分离

曹少杰

（山西交通控股集团有限公司 运城南高速公路分公司，山西 运城 044000）

0 引言

在桥梁健康监测中，应变反映结构的局部受力。应变监测在结构健康监测中具有十分重要的地位，几乎国内外的所有桥梁健康监测系统中，都布设了大量的应变传感器。

大量的运营期监测数据表明，监测应变数据一般具有由长期趋势变化、周期性变化及随机变化等部分效应叠加的。长期趋势变化主要是由混凝土收缩徐变引起，周期性变化主要是由温度变化引起，而随机变化则是由车辆荷载及其他偶然荷载引起。长期趋势及周期性变化是缓慢连续的，而随机荷载变化则是突变和离散的。随机荷载中风荷载及偶然荷载产生的应变较少可以忽略，因此假定随机荷载主要是由车辆荷载引起的。

在桥梁健康监测中，如何实时并准确获得车辆荷载产生的应变效应，并以此进行安全预警，对于掌握结构受力及保障大桥安全具有非常重要的意义。文献[1]采用二次滑动平均法进行应变趋势项解耦，从而获得车辆荷载产生应变，但未明确该方法是实时在线处理还是定期进行离线处理[1]。文献[2]采用改进的移动平均法进行应变测试数据处理，将实测数据分为趋势项和离散项两部分，从而提取出车辆荷载产生应变[2]。但该方法适用于离线分析，不适合在线分析。文献[3]采用小波分析的方法将车辆荷载分离[3]，主要研究应变监测中的温度效应，对车辆荷载效应较少涉及。

本文通过对多种数据处理方法的对比，系统总结各种方法的优缺点，从而寻找出一种适合于在线分析的数据处理方法，提高了数据的实时性和准确性。

1 改进的移动平均法

移动平均法是用一组最近的实际数据值来预测未来一期或几期数据的一种常用方法。其计算方法是：

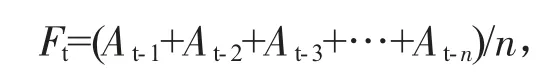
式中：Ft为对下一期的预测值；n 为移动平均的时期个数；At-1、At-2、At-n为前期实际值。

移动平均方法能够用于状态预测。当数据不会迅速或快速增长，移动平均法可以有效地消除数据的随机误差。平滑处理方法将车辆荷载产生的应变看做噪声，是随机出现的（围绕着总体趋势上下摆动），均值为0（表明噪声可能有正有负）。而实际采集的数据却明显与此不同，车辆荷载产生的应变基本上只出现在一个方向。因此，采用传统的平滑处理方法会带来较大的误差，必须对此进行改进。图1 为某桥健康监测中应变实测曲线图，从图中明显看出车辆荷载产生应变大多数为正应变。

文献[2]便是在上述移动平均的基础上进行了改进。根据相对变化量分辨当前数值是否包含车辆荷载影响，选择没有车辆荷载影响的数据采用移动平均法进行平滑分析，从而得出测试数据的总体趋势线。具体方法是：首先确定分离汽车荷载应变的阈值。其次确定初始值，选择数据前端n 个实测值tn，将其平均值作为数据起算的初始值F0。然后以该初始值作为第n+1 阶段的预测值，若｜tn+1-F0｜设定阈值，则将F0与tn+1的平均值作为n+2 阶段的预测值，否则仍以上阶段的预测值作为n+2 的预测值，将tn+1- F0作为车辆荷载的影响值。如此反复循环，当循环次数达到移动平均所需的周期k 时，则以k个数据的平均值即Fn+k=(Fn+k-1+Fn+k-2…+Fn+k)/n 作为下一状态（n+k+1）的预测值，并按照前述方法与实测值进行比较，分离出汽车荷载影响，如此反复循环直至数据结束。采用上述分析方法对能够有效地分离出车辆荷载产生的应变[2]，如图2、图3 所示。

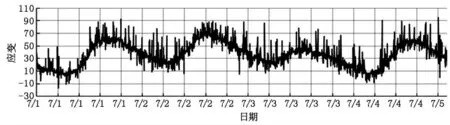
图1 应变实测曲线图

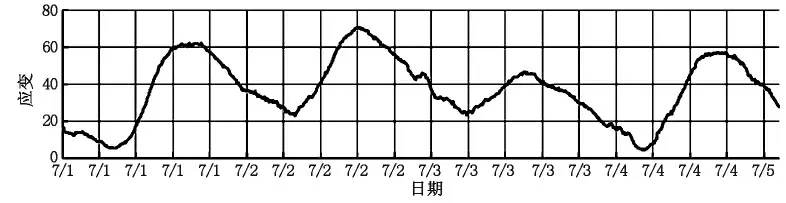
图2 平滑处理后的应变趋势线曲线图

图3 平滑处理后的应变离散线曲线图

然而，在实际应用过程中，发现移动平均法具有如下缺点，无法满足桥梁健康监测的需要：

a）该方法是在收集一个月实测数据基础上进行，具有一定的滞后性，不能及时地识别出车辆荷载，因此也无法进行结构状态实时判断和预警。也就是说采用移动平均法进行车辆荷载识别需要一定长度的数据进行识别，当为实时在线数据时，由于移动平均法的滞后特性，将会造成最新识别的车辆荷载误差较大，因此无法适应在线监测。

b）移动平均法是将所有数据进行平均得到的，实际上由于车辆荷载的随机性，需要对移动平均法进行相应的改进，而改进后的算法由于需要进行反复搜索平滑区段，造成计算速度慢、效率低、且计算机资源占用较大。

2 卡尔曼滤波法

卡尔曼滤波器是线性系统状态方程，是用于通过系统输入和输出观测数据系统状态的最优估计算法。由于观测数据包括系统中的噪声和干扰的影响，最佳估计也可以被认为是上述的滤波处理。

图4 采用卡尔曼滤波法进行数据处理

同样采用卡尔曼滤波法对监测数据进行处理，将车辆荷载产生的应变也视同噪声，从而获得实测数据的总体趋势，将实测原始数据减去总体趋势项，在考虑到应变测试误差的基础上，从而获得车辆荷载产生应变。如图4 所示。

从图4 可以看出，采用卡尔曼滤波法进行数据分析，存在滞后性，得出的应变趋势线与实测应变存在一定的相位差，无法满足项目的实际应用。

3 小波分析

小波变换是采用一个函数的平移伸缩作为基底进行频谱研究。将测试信号的每一个瞬间分量映射到时频平面上的相应位置，该位置正好对应于分量的频率和发生时间，从而将测试信号分解为不同频率及不同时刻的相应测试结果。其中的高频信息能够反映信号的突变，而低频信息则反映着信号的近似形状[4]。

对测试数据进行多层小波分解，根据数据测试结果选择合适的小波基及相应的分解尺度，经多次试算进行4～6 层分解是较为合理的。结果如图5。

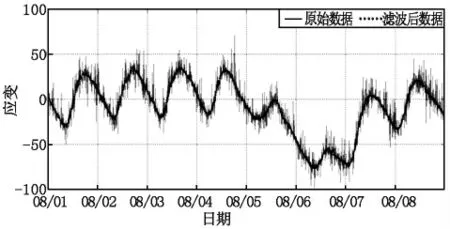
图5 采用小波分析法进行数据处理

图5 中的实线为实测数据，虚线为小波分析后得出的实测曲线中的低频信号也就是近似值，通过选取合理小波基函数及相应的分析尺度，便可将实测曲线中的趋势线与离散线区分出来，从图中可以看出，采用小波分析后的数据与原始数据具有较好的吻合度。

4 健康监测中车辆荷载应变的实时分离

通过上述各种数据处理方法的对比，小波分析在数据处理方面具有一定的优点，但由于需要对一段连续数据进行分析处理，实际监测数据是不断更新的，因此需要分段进行小波分析。

采用上述数据，分段进行小波分析，并与未分段的小波分析结果进行对比，二者在分段的前端与末端均存在一定的截断误差。针对这种情况，采取分段小波分析结合多次修正进行数据处理，每次分段长度取较大值，而时间间隔取较小值，通过多次修正，最终消除截断误差。

根据上述研究成果，在监测系统软件编写过程中，将小波分析编写入采集软件中，实现分段和定时的小波分析，从而确定出应变趋势曲线。基本反映了应变的总体变化规律，得出的车辆荷载应变也反映了大桥实际的受力状况。

5 结语

通过对不同的数据处理方法进行研究，采用分段小波分析进行车辆荷载应变的实时分离是能够满足工程应用的，基本反映了大桥的实际受力状况，通过对车辆荷载产生应变进行统计分析，确定相应的预警阈值，从而可实时判断结构的受力状况，保障大桥的受力安全。