实值优化问题的非对称负相关搜索算法
于润龙 赵洪科 汪 中 叶雨扬 张培宁 刘 淇 陈恩红
1(大数据分析与应用安徽省重点实验室(中国科学技术大学) 合肥 230027)2(天津大学管理与经济学部 天津 300072)
在现实世界中存在许多复杂的优化问题,例如,最小化汽车流体设计的空气阻力[1]、最小化天线阵列中的峰值傍瓣电平(peak side-lobe levels, PSLLs)[2]以及最优经济调度问题中电力设备的折损[3]等.这些复杂优化问题都涉及实值参数空间的许多局部极值解.通常,研究人员设计专门的模拟软件来拟合复杂的优化场景,也就是说显式的优化函数和梯度信息是很难被获取的.这类优化问题被统称为多模态(非凸)实值优化问题或黑盒优化问题[4],图1展示了3个经典的实值优化函数在二维情况下的可视化样例.由于在大多数场景下,缺少对优化函数的有效信息,因此需要采取一般的启发式假设来指导搜索解空间,所有的这些算法被归纳为元启发式搜索[5].大量研究表明[6-8]:元启发式搜索在求解复杂实值优化问题时,展现了比一般遍历方法和其他近似方法更好的优化性能.其中具有代表性的元启发式搜索包括:爬山算法[9](hill climbing, HC)、模拟退火算法[10](simulated annealing, SA)、禁忌搜索[11](tabu search, TS)、遗传算法[12](genetic algorithms, GA)、粒子群算法[13](particle swarm optimizer, PSO)、演化策略[14](evolution strategies, ES)、差分演化[15](differential evolution, DE)等.

Fig. 1 Visualization of benchmark complex real- parameter optimization functions图1 可视化复杂实值优化函数
元启发式搜索是基于一个或多个随机搜索进程以及个体或种群的迭代实现的,种群中的每个个体代表了实值优化问题的一个可行候选解.为了衡量这些解的优劣,需要通过计算实值优化问题的函数值来评估这些候选解,称得到的函数值为个体或解的适应度.适应度的大小通常被用于指导元启发式搜索的搜索方向[16].对于复杂实值优化问题,一方面,由于解空间的维度高、规模大,存在大量的局部极值点,任何包含有限数量搜索进程的元启发式搜索都不能保证发现全局最优解;另一方面,由于解空间的连续性和缺乏优化函数的梯度信息,采用任何随机搜索算子的搜索进程都只能在有限的搜索步骤尽可能接近局部极值点,而不能到达极值点.因此,一个元启发式搜索方法是注重解空间的探索,即探寻更多的局部极值点以发现全局更优的解,还是注重解的利用,即驱使适应度更优的解逼近周围的某个局部极值点,是设计元启发式搜索最为关键的问题之一,相关问题也被称作探索与利用问题,或多样化与集约化问题[17].许多元启发式搜索提出了平衡探索与利用的方法或假设,研究表明这些元启发式假设直接影响了搜索算法的性能[18].特别地,负相关搜索[19](negatively correlated search, NCS)是一种基于种群的元启发式搜索算法,假设不同的搜索进程应当探索解空间不同的区域,通过在并行爬山算法中引入负相关的搜索趋势,目前展现了复杂实值优化问题的最佳优化性能.
在本文中,我们以概率分布建模每一个搜索进程的搜索行为,并且根据其概率分布的大小,将搜索进程的搜索行为进一步划分为全局搜索行为和局部搜索行为.然后提出一种新的元启发式搜索算法,即非对称负相关搜索(negatively correlated search with asymmetry, NSA),它假设具有全局搜索行为的搜索进程应当远离具有局部搜索行为的搜索进程,而具有局部搜索行为的搜索进程不受到具有全局搜索行为的搜索进程的影响.针对元启发式搜索的探索与利用问题,我们通过研究一对搜索进程之间负相关搜索趋势的非对称性,从而提供了一种平衡探索与利用的新的思路.本文首先总结了实值优化问题中元启发式搜索的探索与利用问题和相关假设,然后介绍了经典的并行爬山算法以及负相关搜索的核心思想,接着描述了非对称负相关搜索以及其元启发式假设.相比负相关搜索,可以发现非对称负相关搜索的效率更高且性能更优.在20个多模态实值优化问题上的对比实验验证了我们的想法.最后,讨论了关于非对称负相关搜索在并行计算方面的潜力并给出了扩充实验结果.
1 相关工作
求解复杂实值优化问题的元启发式搜索一般分为2类方法:基于种群的搜索算法(采用一组候选解)和基于个体的搜索算法(采用单个候选解).基于个体的搜索算法首先产生单个随机初始候选解,在每一轮迭代过程中,当前的候选解以一定的概率被其邻域内另一个解所取代;而基于种群的搜索算法利用了多个候选解,在每一轮迭代过程中,整个种群或者部分候选解被新产生的个体取代.由于这2类元启发式搜索导致了不同的探索与利用的平衡策略,我们分别讨论其分支的相关工作.
1.1 基于个体的搜索算法
本节介绍3种经典的基于个体的搜索算法,分别是爬山算法(hill climbing, HC)、模拟退火算法(simulated annealing, SA)和禁忌搜索(tabu search, TS).这3种基于个体的元启发式搜索可以通过独立地并行工作转化成为基于种群的搜索算法,但是大多数情况下使用它们基于个体的搜索形式[9-11].
1) 爬山算法
爬山算法是最基本的元启发式搜索之一,通常被形式化为单个搜索进程,也就是说,从单个随机初始候选解开始,在迭代的过程中被邻域内适应度更优的候选解取代.爬山算法有许多实现方式,其中采用高斯变异算子的实现方式是处理实值优化问题最流行的方法之一[20].为了平衡探索与利用,高斯变异算子的搜索步长由1/5成功准则进行调整.1/5成功准则的核心思想是[21]:如果搜索进程经常在过去的迭代过程中找到适应度更优的候选解,则应当增大搜索步长;如果搜索进程未能在过去的迭代中找到适应度更优的候选解,则搜索步长应当减小.
2) 模拟退火算法
与爬山算法相比较,模拟退火算法采用概率方法更好地探索全局最优解.受冶金退火工艺的启发,模拟退火算法采用加热和冷却的控制策略调整搜索进程远离局部极值点的能力.在模拟退火算法中,缓慢地实施冷却的概念被解释为:随着解空间的探索而接受适应度较差的候选解的概率被缓慢地降低.这意味着在迭代过程中,模拟退火算法的平衡策略从探索转向利用.
3) 禁忌搜索
禁忌搜索通过放宽爬山算法的取代条件和引入禁忌列表来加强对解空间的探索能力.首先,在每一轮的迭代过程中,如果当前候选解的邻域内没有发现适应度更优的解,则可以接受适应度更差的解.然后,引入禁令以阻止搜索进程访问之前发现的解.特别地,如果在短期内访问过某个候选解,或者候选解违反了预先制定的禁忌规则,将该候选解标记上禁令并存放在禁忌列表中,以便搜索进程不会反复搜索这个候选解,这有助于算法对解空间的探索能力.
1.2 基于种群的搜索算法
研究表明[6-8],基于种群的搜索算法不仅在理论方面取得了成功,而且在应用方面被认为是经验上更好的元启发式搜索.尽管有许多工作讨论了基于种群的探索与利用的平衡策略,但是可以从整体上把它们分为3类[19,22-23]:
1) 小生境技术(niching techniques)
诸如适应度共享和拥挤方法的小生境技术旨在选择解空间中彼此距离较远的一组候选解,然后利用这些解产生新的候选解(一般通过杂交算子).适应度共享方法试图与邻域的个体共享适应度,并通过牺牲部分候选解的适应度来维持种群的多样化.而拥挤方法依赖于后代与其近代父母之间的竞争机制,允许调整选择压力以偏向选择相隔距离很远的个体,从而增进种群的多样化.
2) 自适应搜索步长(adaptive search step-size)
显然,可以采用具有小搜索步长的搜索进程来发现更接近当前候选解的新的解,这有助于利用适应度更优的候选解.另一方面,可以采用具有大搜索步长的搜索进程来发现更远离当前候选解的新的解,这有助于解空间的探索.许多元启发式假设基于解空间的属性提出了自适应搜索步长的策略.但是,这种方法会引入另一个算法设计问题,也就是说,应该使用何种搜索进程及在迭代期间何时切换具有不同搜索步长的进程以实现探索与利用之间的良好折中.
3) 负相关(negative correlation)
基于并行爬山算法的负相关提出元启发式假设,即不同的搜索进程应该在解空间中搜索不同的区域.通过将各搜索进程的搜索行为建模为概率分布,负相关搜索鼓励保留那些具有较小相关概率的搜索进程.由于搜索进程之间搜索趋势的负相关性,负相关搜索显著提高了探索能力,我们将在接下来的章节详细介绍这一策略.
2 并行爬山算法与负相关
在本节中,首先介绍面向实值优化的并行爬山算法(parallel hill climbing, PHC)框架,然后在此基础上进一步讨论负相关搜索.并行爬山算法被形式化为多个爬山算法独立且并行地运行,每个爬山算法从初始的随机候选解开始,在迭代期间被适应度更优的邻居候选解取代.我们可以将爬山算法视为单个搜索进程,其在大部分情况下是依赖高斯变异算子实现的,通过1/5成功准则调整高斯变异算子的参数.
2.1 高斯变异算子
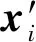

(1)
xi d表示xi的第d维分量,N(0,σi)表示一个均值为0且标准差为σi的高斯随机分布.高斯随机分布的标准差σi对于不同的搜索进程以及其在解空间不同的维度可以给出不同的值,为了保持简单的形式,在本文默认初始化所有搜索进程相同的高斯变异算子的参数.对于并行爬山算法,采取下启发式规则来选择丢弃一个解:

(2)
2.2 搜索步长与15成功准则
通过高斯变异算子的数学形式,可以了解到一个候选解产生新的解的范围(新的个体与其父亲在解空间的欧氏距离)依赖于高斯随机分布的标准差σi值.因此在并行爬山算法中,对于单个搜索进程来说,高斯随机分布的标准差σi值可以被看作调整搜索步长的重要指标.15成功准则被经常用于协助基于高斯变异算子的搜索进程,特别地,调整搜索步长以谋求探索与利用之间的平衡.一般的15成功准则可以表示为[21]

(3)
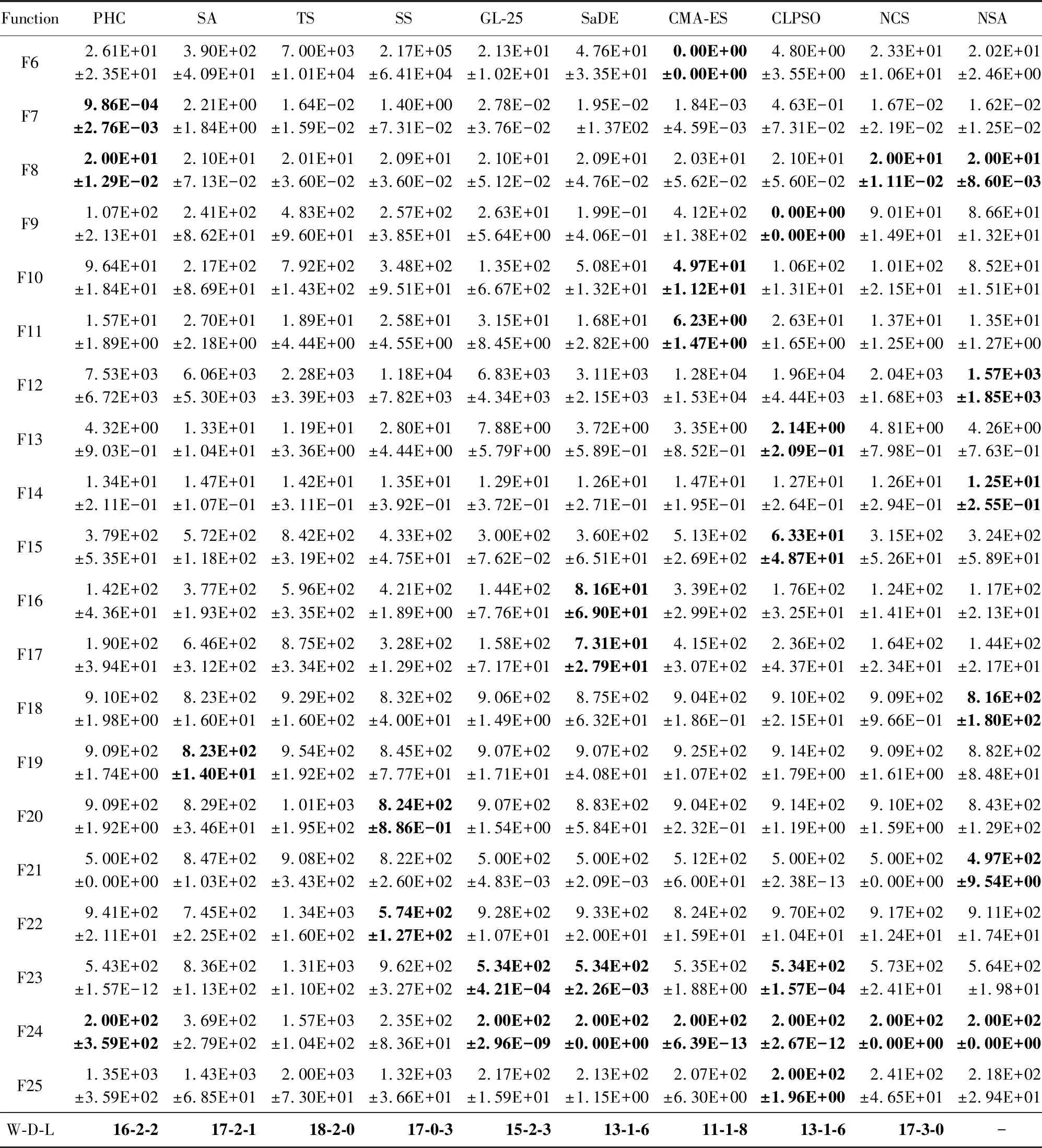
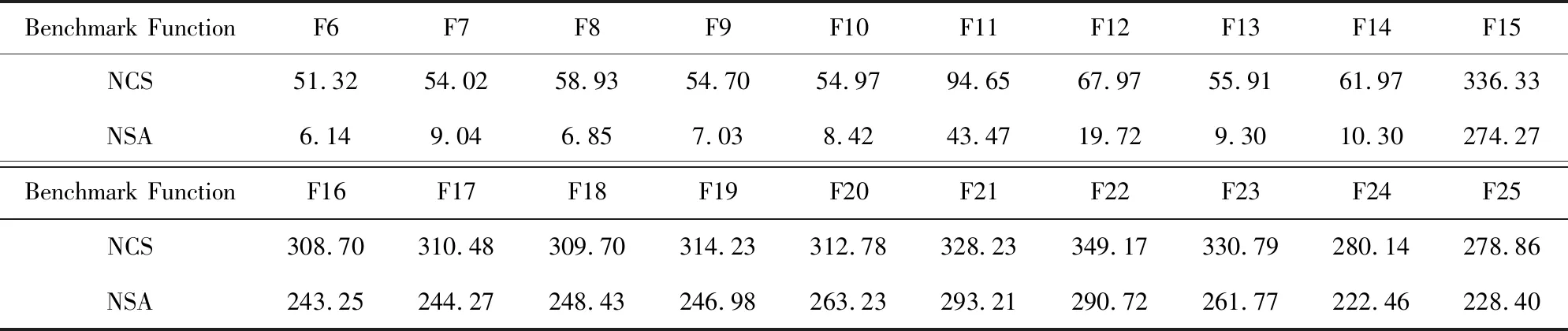
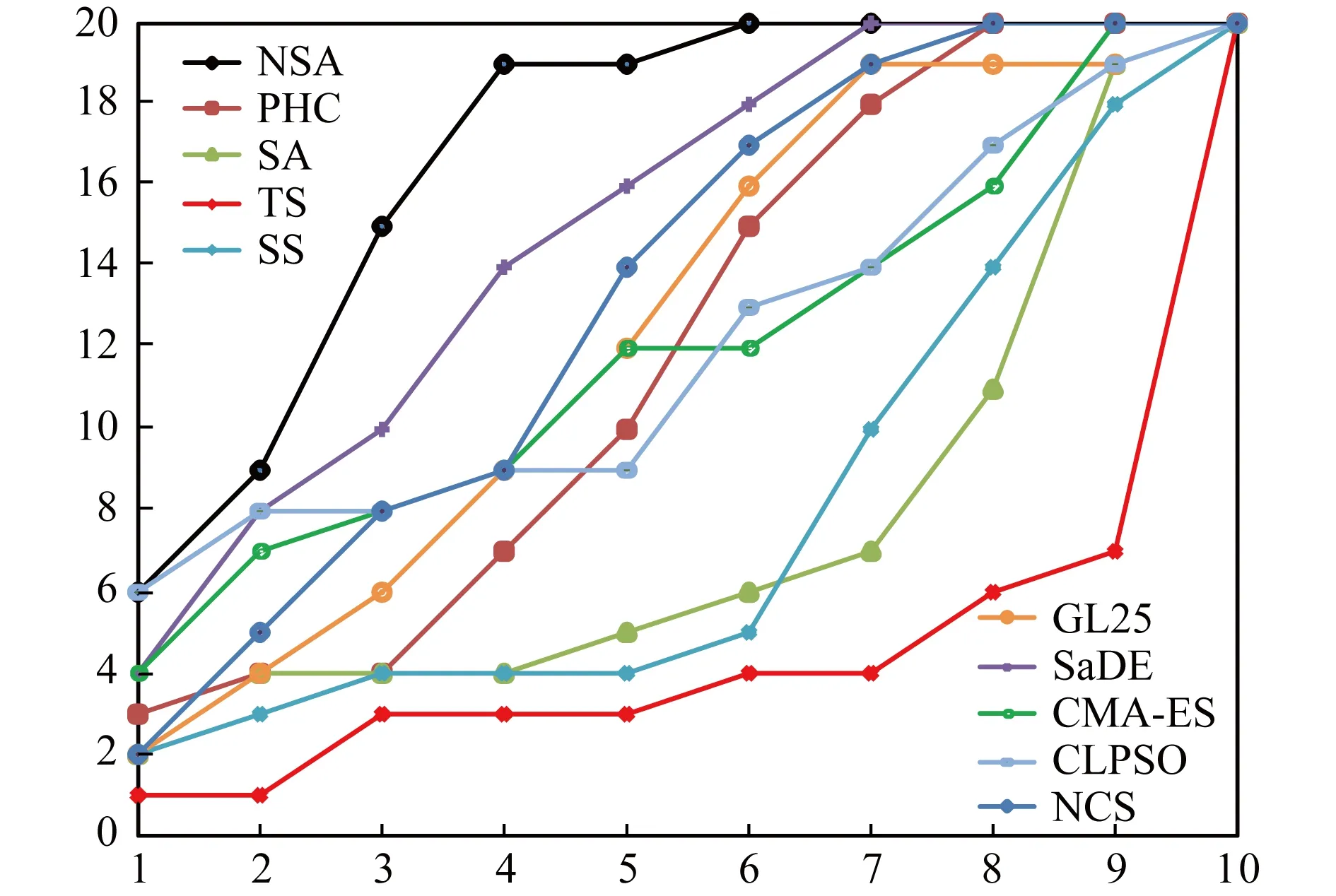
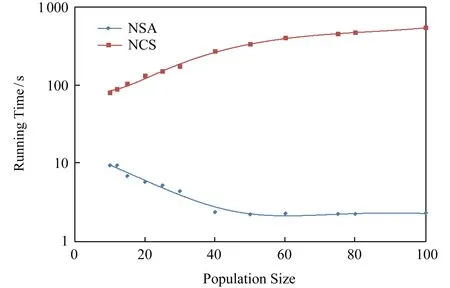
其中,0 负相关搜索首先将搜索进程的搜索行为视为概率分布,因为新的解是在每次迭代时由变异算子作用于候选解产生的,并且下一次迭代中搜索进程的搜索趋势相当于一个新的解被采样的概率分布.因此,如果一个搜索进程的搜索行为与其他搜索进程的搜索行为负相关,则很可能在不被其他搜索进程的搜索行为覆盖的区域产生新的候选解.这需要测量2个概率分布之间的差异或相关性,巴氏距离(Bhattacharyya distance)被引入并测量2个搜索进程的搜索行为之间的相关性[24].对于2个连续或离散概率分布的巴氏距离可以分别表示为 (4) (5) 其中,pi和pj表示2个分布的概率密度函数.如果无法获知显式的概率密度函数,可以通过随机产生候选解的方式来近似概率,并通过巴氏距离的离散形式估计相关性的值. (6) 其中,概率分布pi表示了第i个搜索进程的搜索行为.Corr(pi)的值越大,与其相关联的候选解越倾向于被保留. 在本节中,首先讨论负相关搜索的局限性.针对负相关搜索的缺陷,提出将非对称的思想引入负相关,根据搜索行为的概率分布的大小,将搜索行为进一步划分为全局搜索行为和局部搜索行为,并给出非对称负相关搜索作为算法实例. Fig. 2 Illustration of search behaviors in a two-dimensional search space图2 二维解空间(标注等高线)的搜索示例 除负相关搜索之外,几乎所有的元启发式假设都将多样性概念定义为各个候选解之间的多样性,而负相关搜索提出并定义了搜索行为的多样性,这直接与搜索进程产生新解的概率分布相关.负相关的思想有效改进了并行爬山算法的搜索性能.然而,本研究认为不同的搜索进程覆盖不同的搜索区域(具有负相关的搜索行为)过于严格.举例来说,如果多个搜索进程共同覆盖的解空间的区域存在局部极值点,那么这些搜索进程互相远离的结果将导致其中的局部极值点不被任何一个搜索进程发现.在局部极值点密集的区域,这种情况尤为明显.当搜索进程共同覆盖的解空间的区域较小且集中多个局部极值点时,负相关不仅不能够更好地探索解空间,而且还会导致搜索进程拥挤,这大大降低了搜索效率. 考虑图2所描述的情形,R1和R2表示2个搜索进程在二维解空间采纳负相关的搜索行为,在图例中其搜索趋势以箭头符号示意.对于R1和R2,我们以候选解的向量值为圆心,高斯变异算子的标准差为半径,可视化2个搜索进程在二维解空间的搜索范围,即搜索进程覆盖的解空间的区域.可以发现,R1和R2的搜索范围覆盖了部分相同的区域,且共同覆盖的区域存在局部极值点A.由于负相关鼓励搜索进程探索解空间不同的区域以维持解的多样性,因此R1和R2倾向于在远离彼此的方向上产生新的解,从而远离局部极值点A.对于这种情形,2个搜索进程无法利用当前候选解发现邻域内适应度更优的新的解,可以认为负相关限制了搜索进程对解的利用,破坏了探索与利用的平衡. 为了平衡探索与利用的关系,我们首先根据一对搜索进程其搜索范围的相对大小,将种群中的搜索进程的搜索行为划分为全局搜索行为(搜索范围较大)和局部搜索行为(搜索范围较小).一方面,具有全局搜索行为的搜索进程搜索范围大、搜索方向相对不清晰、其覆盖的区域可能存在多个局部极值点或者没有局部极值点;另一方面,具有局部搜索行为的搜索进程搜索范围小、搜索方向相对清晰其覆盖的区域通常只有一个或少个局部极值点.我们区别对待具有全局搜索行为的搜索进程与具有局部搜索行为的搜索进程对彼此相关性的影响,并提出非对称负相关的元启发式假设:如果一对搜索进程中存在具有全局搜索行为的搜索进程,那么这个搜索进程应鼓励与另一个搜索进程负相关的搜索行为.也就是说,具有全局搜索行为的搜索进程应当远离具有局部搜索行为的搜索进程,而具有局部搜索行为的搜索进程不受到具有全局搜索行为的搜索进程的影响.通过引入非对称到负相关,我们提供了一种平衡探索与利用的新的思路,并且可以大量节省由负相关操作产生的计算成本,从而节约算法的运行时间. 下面介绍一种采纳非对称负相关的元启发式假设的实例,即非对称负相关搜索算法.非对称负相关搜索继承了并行爬山算法的基本形式,种群中的个体依赖高斯变异算子产生新的解.特别地,高斯变异算子的标准差成为刻画个体搜索行为的重要指标.对于第i个搜索进程,当前高斯变异算子的标准差为σi,对于第j个搜索进程,当前高斯变异算子的标准差为σj,如果存在σi>σjW,定义第i个搜索进程相对于第j个搜索进程是具有全局搜索行为的搜索进程,第j个搜索进程相对于第i个搜索进程是具有局部搜索行为的搜索进程,反之亦然,如果不存在σi>σjW或者σj>σiW,定义第i个搜索进程与第j个搜索进程互为具有局部搜索行为的搜索进程,这里W被定义为非对称参数.对于当前一对搜索进程,具有局部搜索行为的搜索进程不受到相关性的影响.如果一个搜索进程相对于其他所有搜索进程均为具有局部搜索行为的搜索进程,那么它的候选解的更新策略只与解的适应度有关,这与并行爬山算法的候选解的更新策略是一致的. 如果一个搜索进程相对于某个搜索进程具有全局搜索行为,那么就需要计算它与这个搜索进程的相关性.由此,在非对称负相关搜索中,相关性为 (7) 对于采用高斯变异算子的2个个体xi和xj,其产生子代的概率分布的巴氏距离[25]: (8) 其中,Σ=(Σi+Σj)2,Σi=σi2I,I是单位矩阵.进一步平衡种群中个体的适应度与相关性之间的关系,因为个体的适应度f(xi)和相关性Corr(pi)通常不在一个量级,并且个体的适应度f(xi)可能取负值,而相关性Corr(pi)是非负的.对于最小化问题,我们采取的策略是f(xi)减去目前为止搜索算法得到的最小值,作非负化处理.然后,对于第i个搜索进程,做归一化处理,使得和Corr(pi)+都等于1.归一化处理之后,可以不再考虑f(xi)和Corr(pi)的大小,因为现在它们等于和一个较小的表示有较优的适应度,一个较大的表示产生的子代会与那些具有局部搜索行为的个体产生的子代处于较远的距离.因此,那些更小且更大的解将会倾向于被保留.我们采用启发式规则来选择丢弃一个解: (9) (10) 其中,t是当前迭代的轮数,Tmax是非对称负相关搜索迭代的总轮数. 由此,我们可以得到非对称负相关搜索的算法流程:首先产生N个随机候选解作为初始种群,记录下初始种群的最优解,进入迭代过程.每一轮迭代,一个随轮数变化的λ值被产生,N个新的解由高斯变异算子作用在父代上产生,考察新产生的解的适应度并更新最优解,然后根据其搜索行为选择式(2)或者式(9)决定新的解是否替换父代成为种群中的个体.每经过epoch轮迭代,根据15成功准则更新高斯变异算子的标准差.终止条件被满足时,迭代结束,返回最优解,算法终止. 在本节,为了评估非对称负相关搜索(negatively correlated search with asymmetry, NSA)的潜力,我们在实验部分与许多成熟的基于种群的搜索算法进行比较,包括遗传算法(genetic algorithms, GA)、粒子群算法(particle swarm optimizer, PSO)、演化策略(evolution strategies, ES)、差分演化(differen-tial evolution, DE)和散点搜索[26](scatter search, SS).对于这些算法中的每一种,选择最新的版本用于比较,即GL-25[12],CLPSO[13],CMA-ES[14],SaDE[15]和SS[26].此外,还选取了2个流行的基于个体的搜索算法,即模拟退火算法[10](simulated annealing, SA)和禁忌搜索[11](tabu search, TS),因为它们在实践中取得了优异的性能.为了验证非对称负相关的元启发式假设,选取并行爬山算法(parallel hill climbing, PHC)和负相关搜索[19](negatively corre-lated search, NCS)做参照.我们根据文献中的建议设定上述算法的参数,给出了实验结果及分析.最后,讨论了关于非对称负相关搜索在并行计算方面的潜力并给出了扩充实验结果. 为了使比较公平,对所有的搜索算法设定相同的产生初始解的策略,并用实值向量的形式表示候选解.SA[10]和TS[11]采取相同的高斯变异算子,其中标准差被初始化为优化函数自变量范围的1/10,式(3)中的参数r和epoch分别设定为0.99和10.具体地,对于SA中的冷却过程,温度初始化为1,然后每100轮迭代以85%的速率降低;对于TS,将最近生成的5个候选解保存在禁忌列表中.遵循标准程序,设定SS[26]的参考集的大小为10,并且参考集中的每一对候选解在迭代中被重新组合以产生新的解,特别地,使用1点杂交算子作为父代的重组方法,使用高斯变异算子产生并改进新的解.在本实验中,我们比较了标准的CMA-ES[14].GL-25[12]是一种混合实值编码的遗传算法,它首先在25%的计算预期内执行全局搜索行为,然后执行局部搜索行为,其中与全局搜索行为相关的初始种群大小为400,之后适应度最高的100个个体被保留并执行局部搜索行为.在CLPSO[13]中,通过利用所有粒子的历史最佳信息来更新粒子的速度.在SaDE[15]中,尝试矢量生成方案和相关控制参数都是通过逐次学习以前产生的适应度更优的候选解及其经验而自适应.CLPSO和SaDE的种群规模分别为40和50.除了相关性的计算过程之外,PHC和NCS[19]复制NSA的所有组件.也就是说,在PHC中,适应度是被认为是丢弃一个候选解的唯一标准.对于NSA,设定非对称参数W=10,我们还需要预先设定NSA的种群大小,在这里将其设定为10,即与SS相同. 多模态(非凸)实值优化问题是最典型的复杂实值优化问题,也正是这类问题激发了大多数基于种群的搜索算法的设计.在实验评估中使用CEC2005实值优化竞赛[27]的基准测试函数(编号F6~F20)中20个多模态实值优化问题.每个基准测试函数的维度设置为30维.每个搜索算法在生成300 000个候选解时终止,并输出到目前获得的适应度最优的解.最优解的质量用函数误差测量,即所获取的最优解的目标函数值与问题的最佳候选解的目标函数值(这些基准测试函数已知)之间的差值.也就是说,更优的解对应于更小的函数误差,零函数误差表示找到了最佳的候选解.由于所有的搜索算法都采用随机搜索算子,我们对每种算法重复实验25次,记录相应的函数误差值,并将10种算法实现的平均函数误差与标准偏差一起列出. 表1给出了10种搜索算法在20个基准测试函数上的平均函数误差,表2给出了非对称负相关搜索与负相关搜索在基准测试函数上运行时间的比较.我们使用双侧Wilcoxon秩和统计检验[28]来检查非对称负相关搜索与对比搜索算法之间的差异(就函数误差而言)是否具有统计显著性,Wilcoxon秩和统计检验以0.05显著水平设计.通过Wilcoxon秩和统计检验,如表1最后一行所示,在成对的比较中,非对称负相关搜索在统计上显著优于其他算法,特别地,非对称负相关搜索在20个基准测试函数上均不显著劣于负相关搜索,并在17个基准测试函数上显著优于负相关搜索,验证了非对称负相关假设的合理性.并且,在运行时间的比较中,非对称负相关搜索因为缓解了负相关搜索冗余的相关性计算,在许多基准测试函数与负相关搜索相比大大节约了运行时间.此外,我们基于成对的双侧Wilcoxon秩和统计检验计算了搜索算法执行第K佳结果的次数,即Top-K(K=1,2,…,10),如图3所示.如果算法的整体性能是最优的,那么对应的折线会高于其他算法的折线,并且在最小的K值达到20(基准测试函数的总数).可以观察到非对称负相关搜索在K=6时首先到达了20,同时非对称负相关搜索永远不会低于其他折线,因此我们验证了非对称负相关搜索取得最佳的整体性能. Table 1 The Averaged Results of Search Algorithms on Benchmark Functions表1 搜索算法在基础测试函数上的平均函数误差 Note: The averaged results are listed in the form of “mean ± standard deviation”. The last row provides the results of the Wilcoxon test, where “W-D-L” indicates NSA is superior to, not significantly different from or inferior to the corresponding compared algorithms. Table 2 The Running Time of NSA and NCS表2 非对称负相关搜索与负相关搜索的运行时间 s Fig. 3 The Top-K,K=1,2,…,10,curves of the algorithms图3 搜索算法的Top-K(K=1,2,…,10)折线图 Fig. 4 The search trajectories of three algorithms with population size N=4 on the 2D version of F18图4 在二维基准测试函数F18上3种算法的搜索轨迹 为了进一步验证非对称负相关的元启发式假设,在二维可视化的基准测试函数上设计实验测试非对称负相关搜索,并比照了并行爬山算法和负相关搜索.我们设定种群的大小为4,在搜索过程中记录每个个体的搜索趋势.在基准测试函数F18上的结果如图4所示.可以观察到并行爬山算法探索解空间的能力很差,解的多样性在迭代的过程中不能够被很好地保持;负相关搜索拥有优异的探索解空间的能力,有效地保持了解的多样性,但是限制了对优质解的利用,不能够很好地做到集约化;非对称负相关搜索在探索解空间的同时,有效地利用了高质量的解.综上所述,可以认为非对称负相关的元启发式假设在探索与利用之间做到了最优的平衡. 因为元启发式搜索是递归算法的特性,对于元启发式搜索细粒度的并行化方法(基于个体间的并行),如果不面向个体的适应度计算做单独的并行设计,元启发式搜索并行化的最大效率不会超过种群大小,所以对大种群更友好的元启发式搜索并行化潜力更大,通常是更被青睐的算法.特别地,基于种群的搜索算法通常因为个体间频繁的信息交流与现实中昂贵的通信代价,导致并行化效率较低,无法谋求以种群规模交换迭代轮数的目的[29],因此消除个体之间不必要的通信可以很好地释放算法的并行潜力.这里设计实验研究了非对称负相关搜索在并行化方面的性能,并与负相关搜索进行比较.具体地,采用细粒度的“主-从模型”作为并行框架[30],如图5所示,主机负责控制搜索流程,每个计算单元享有一个独立的搜索进程,搜索进程之间的通信由主机转接.实验硬件环境为英特尔至强多核服务器集群,软件环境为Matlab分布式计算系统.设定搜索算法的种群大小从10增大到100,相应地计算单元由10个扩充到100个,并且保持搜索算法在生成300 000个候选解时终止,也就是说迭代轮数从30 000轮减少到3 000轮,记录下平均函数误差与算法运行时间的变化. Fig. 5 Fine-gained Master-Slaves parallel framework图5 细粒度的“主-从模型”并行框架 在30维基准测试函数F7上的结果如图6和图7所示.通过观察图6可以得到,对于最小化基准测试函数,我们保持搜索算法生成候选解的个数,在牺牲迭代轮数的同时扩大种群的规模,搜索算法的性能受到不同程度上的影响.其中,非对称负相关搜索对于种群规模较大的情况适应较好,负相关搜索在种群规模极大的情况搜索性能急剧下降,两者的相对差值呈多项函数趋势.这是由于负相关搜索在种群规模极大的情况容易出现因负相关产生的拥挤现象,也就是说个体集中在局部极值点附近且流通性较差.非对称负相关的元启发式假设只关注全局搜索行为,促进了个体的流通,有效缓解了拥挤现象,对基于大种群的大规模并行环境更友好.通过观察图7可以得到,在生成候选解的个数不变的情况下,非对称负相关搜索可以通过细粒度的并行化方法有效节约运行时间,并且种群规模越大,运行时间越短,这得益于随着种群规模扩大时算法迭代轮数减少.同时,并行化负相关搜索的运行时间随着种群规模的扩大反而急剧提升,这是由于种群规模扩大导致整体相关性的计算代价呈幂律提升,从而展现了负收益的并行化结果.非对称负相关的元启发式假设避免了部分冗余的相关性计算,在大规模并行环境展现了更加优异的潜力. Fig. 6 The function errors of parallelized NSA and NCS图6 并行化NCS,NSA的平均函数误差及相对差(Diff) Fig. 7 The running time of parallelized NSA and NCS图7 并行化NSA以及并行化NCS的运行时间 本文首先介绍了求解复杂实值优化问题的一般性方法和关于探索与利用的背景研究,然后围绕平衡探索与利用的策略分析了流行的元启发式假设,特别是负相关.我们发现负相关搜索鼓励搜索行为的多样性从而改进了并行爬山算法的探索能力,但是其假设过于严格,并且导致搜索进程的拥挤和相关性计算的冗余.我们提出了非对称负相关的元启发式假设,将种群中搜索进程的搜索行为划分为全局搜索行为和局部搜索行为,鼓励具有全局搜索行为的搜索进程尽可能远离具有局部搜索行为的搜索进程.在此基础上,我们给出了非对称负相关搜索的算法流程,并在20个多模态实值优化问题上与成熟的搜索算法对比,实验结果表明非对称负相关搜索取得了最佳的整体性能,同时在运行效率和并行化潜力方面显著优于负相关搜索. 元启发式搜索是通过全局探索和局部利用的不同机制引导并迭代生成解的一类过程,探索与利用之间的平衡是提高元启发式搜索优化性能的关键因素,不同的平衡策略是区分许多元启发式搜索的重要标识.本文继承了负相关对于搜索行为多样性的概念,与此同时关注解的利用,面向复杂实值优化问题,提供了一种平衡探索与利用的新思路.未来的研究包括:1)关于非对称负相关搜索的理论研究,比如发现最优解的时间复杂度分析;2)将非对称负相关搜索扩展到其他优化问题,比如,多目标实值优化问题,组合优化问题,多任务优化问题等;3)利用非对称负相关搜索解决具体的复杂应用问题.2.3 搜索行为与负相关
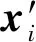

3 非对称负相关搜索算法
3.1 负相关的局限性

3.2 非对称负相关搜索
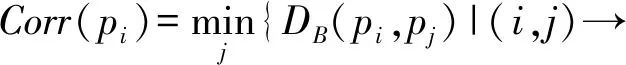
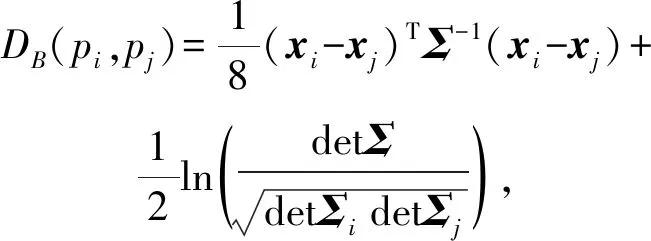

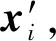

4 实验评估
4.1 搜索算法的参数设置
4.2 实验方案
4.3 实验结果与分析

4.4 非对称负相关搜索的并行化

5 总 结

