声场波数积分最大截止波数自动选取算法*

刘 巍，肖汶斌，程兴华，王勇献，张理论

(国防科技大学 气象海洋学院， 湖南 长沙 410073)

声波能够在海水介质中远距离传播，是目前获取水下信息的主要载体，因此水下声传播特性的精确、高效计算始终是各军事强国的重要研究方向[1]。水声传播的物理过程受波动方程控制，由于声压是空间与时间的四维变量，直接求解计算量巨大。潜艇等水下兵器的声频谱一般具有窄带特性，因而通常将时域内的波动方程采用傅立叶变换转为频域内空间三维Helmholtz方程，每次只针对特定频率的声场进行计算，使声场求解难度有所降低[2]。由于Helmholtz方程属于椭圆型方程，直接采用有限差分、有限元法离散需要建立方程组迭代求解，这对于追求时效性的水声军事应用来讲计算量仍显过大，因此实际中经常通过各类假设对Helmholtz方程进行简化，衍生出波数积分法、简正波法、抛物方程法、射线法等水声模型[3]。

对于水平分层的理想声学介质，波数积分法没有模型误差，被称为“精确解”，广泛应用于海洋声场仿真、海洋声学参数反演与目标定位匹配场反演[4-6]。然而，波数积分采用传递函数矩阵法计算积分核函数时会遇到计算不稳定问题(出现NaN(not a number)而崩溃),虽然减小无限波数谱的截止波数可以提高稳定性，但波数积分过程的数值精度也将随之降低。数值计算稳定性问题较难采用理论分析方法事先准确判断，故目前尚无自动算法能够获得稳定的、尽可能大的截止波数。

目前关于波数积分法计算稳定性的研究较少，骆文于等[7]针对Pekeris波导问题(单层水体)，对深度采用局部坐标，提出了一种稳定的波数积分算法。本文对波数积分传递矩阵法自下而上(单向)、上下对进(双向)两种计算顺序进行了分析，提出了基于预估-校正思想的最大截止波数自动选取算法。

1 理论模型

在介质水平分层假设下(介质密度、声速、吸收系数在各层内部均匀，隐含声压二维轴对称性质)，可采用Hankel变换将声场Helmholtz方程转换成如式(1)所示波数积分形式。

(1)

其中：P为频域相对声压(参考点位于距声源点1 m处)；J0(krr)为Bessel函数；φ(kr,z)为波数积分核函数[3]，且φ(kr,z)满足深度方程

(2)

式中，k为声场介质波数，z为竖直方向坐标，zs为声源深度，δ为狄拉克函数。深度方程的求解是波数积分法的关键内容，求解方法包括传递函数矩阵法、直接全局矩阵法、不变嵌入法等[3]。其中传递函数矩阵法具有解析形式，计算精度高、算法形式简单，本文即针对该方法的不稳定问题提出最大截止波数自动选取算法。

1.1 传递函数矩阵

首先将声场按照需要划分成若干水平层，并保证在声源点深度zs存在一个分界面，各层与其分界面编号如图1所示。

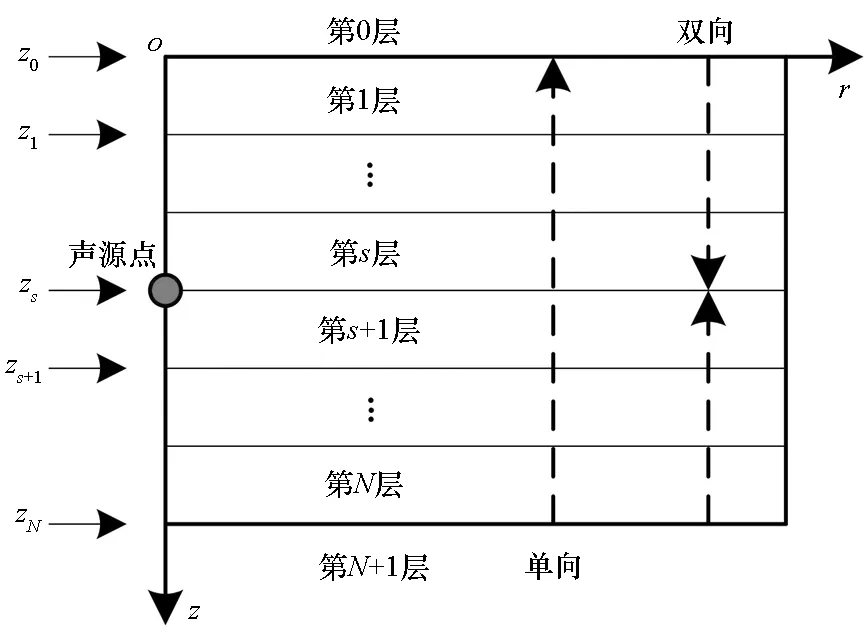
图1 声场介质分层示意图Fig.1 Sketch of acoustic multilayers

由于在各层声介质内部声学参数均匀且无声源，因此在第m层的深度方程形式为

(3)

(4)

(5)

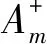
(6)

式中，ρm为第m层的密度，ω=2πf为角速度。若令Γm=kz,m/(ρmω)，则

(7)

进而写出第m层声矢量

(8)

其中，

(9)

(10)

根据第m层声矢量表达式可得第m层的上界面zm-1处声矢量为

vm(kr,zm-1)=cm(kr,zm-1)am(kr)

(11)

第m层的下界面zm处声矢量为

vm(kr,zm)=cm(kr,zm)am(kr)

(12)

将式(11)、式(12)结合可得声矢量传递迭代式

vm(kr,zm-1)=Mm(kr)vm(kr,zm)

(13)

式中，Mm(kr)即为第m层的传递矩阵，

(14)

式中，hm=zm-zm-1代表第m层厚度，双曲余弦、正弦函数表达式为

cosh(ikzhm)=(eikzhm+e-ikzhm)/2

(15)

sinh(ikzhm)=(eikzhm-e-ikzhm)/2

(16)

1.2 声源界面条件与上、下边界条件

1.2.1 声源界面条件

声源界面处的声压连续，但垂直振速不连续，存在点源条件

(17)

1.2.2 上边界条件

在上边界外侧(第0层)

(18)

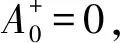
(19)

第0层下边界的垂直振速为

(20)

令w0(kr,z0)与φ0(kr,z0)之比为

(21)

则从声矢量中提出振速后形式为

(22)

需要指出的是，计算域上边界以上部分(第0层)取不同密度值时，可表示不同的上边界类型：①当ρ0=0时(真空)，表示绝对软边界；②当上边界以上密度取第一层水体密度(即ρ0=ρ1)时，表示自由空间的开边界；③当上边界以上密度取无穷大值(即ρ0→∞，实际取很大的正数)时，表示绝对硬边界，声波不能进入该介质，边界上质点法向振速为0(当ρ0→∞时，-Γ0→0、w0(kr,z0)→0)。

1.2.3 下边界条件

在计算域下边界外侧(第N+1层)

(23)

(24)

在第N+1层上边界zN处的垂直振速为

(25)

令φN+1(kr,zN)与wN+1(kr,zN)二者之比为

(26)

则从声矢量中提出振速后形式为

(27)

与上边界同理，下边界以下部分(第N+1层)取不同密度值时，可表示不同的下边界类型。

1.3 自下而上(单向)传递求解方法

传递函数矩阵法的声矢量传递顺序主要有两种：一种是自下而上(单向)传递计算各界面声矢量；第二种是分别从下边界与上边界(双向)传递求解至声源界面。本小节讨论单向传递。

1)通过声矢量迭代式从下至上计算声源点界面紧下方声矢量。在声源下方区域，各分层界面处的声压与垂直振速应连续，因此下层上界面的声矢量与相邻上层下界面的声矢量相等，即

vm(kr,zm)=vm+1(kr,zm)

(28)

这样即可通过声矢量迭代式(13)一层一层地将最下层信息传递到声源点界面紧下侧，获得vs+1(kr,zs)。

2)根据声源界面条件计算出声源点界面紧上侧声矢量。在声源点界面，声压保持连续，垂直振速存在间断，如式(17)，令

(29)

则声源点界面紧上侧声矢量为

vs(kr,zs)=vs+1(kr,zs)-Δv(kr,zs)

(30)

3)从声源点界面紧上侧开始，继续向上传递计算声矢量，直至到达第一层上界面，获得v1(kr,z0)。

4)根据最上层下界面声向量v0(kr,z0)=v1(kr,z0)求出未定量wN+1(kr,zN)与w0(kr,z0)，进而可计算出各位置的φ(kr,z)。

1.4 上下对进(双向)传递求解方法

单向与双向传递求解方法实质上都是以上边界振速w0(kr,z0)与下边界振速wN+1(kr,zN)为未知数，以分层界面声压连续、振速连续(除声源界面外)建立两个方程，进行封闭求解。双向传递求解方法为：

1)通过声矢量传递迭代式，从下至上计算声源界面紧下侧声矢量vs+1(kr,zs)。

2)通过声矢量逆迭代式从上至下计算声源界面紧上侧声矢量。逆传递迭代式为

(31)

通过自上而下逐层迭代可得vs(kr,zs)。

3)根据声源界面条件(点源条件)计算出声矢量未知数。在声源界面上

vs+1(kr,zs)-vs(kr,zs)=Δv(kr,zs)

(32)

通过该式可计算出未知数wN+1(kr,zN)与w0(kr,z0)，进而可计算出各位置的φ(kr,z)。

1.5 最大截止波数自动选取算法

在数值计算过程中，需要对无限波数谱进行适当截止，并将积分离散为有限项求和

(33)

式中，kmax称为截止波数。若kmax过大，可能导致计算发散[3]；若kmax过小，波数积分误差就会增大(在声源深度附近界面上误差更大)。因此为了准确计算各个深度的声压，就需要在保持计算稳定的情况下，选取尽可能大的截止波数(下文称其为最大截止波数)。

2 算例测试

为便于直观判断计算结果的正确性与精确度，采用具有解析解的自由空间球面波算例进行算法测试，声压解(R为到声源点的距离)为

P=eikR/R

(34)

2.1 单向求解

采用单向求解方法，最大截止波数自动选取，得kmax=2.9k=1.84。由于自由空间球面波声源上、下两侧具有对称性，因此声源下方50 m与上方50 m深度上的积分核函数幅值随水平波数变化曲线应一致，如图2所示，其中图2(a)所示的声源下方50 m处核函数幅值Abs(φ)是正确值，图2(b)所示的声源上方50 m处核函数“发散”。事实上，单向传递算法的核函数在通过声源深度后很快就出现“发散”，使该位置以上的所有深度核函数的“发散”程度越来越大。

(a) 声源下方50 m(z-zs=50 m)(a) 50 m under source depth(z-zs=50 m)

(b) 声源上方50 m(z-zs = -50 m)(b) 50 m above source depth(z-zs= -50 m)图2 球面波积分核函数幅值，单向求解(f=150 Hz)Fig.2 Wavenumber kernel function amplitude of free space spherical wave, bottom-to-top propagator(f=150 Hz)

如果各深度采用相同截止波数的传统方法进行积分，则单向求解的传播损失云图如图3(a)所示，显然在核函数发散的区域，声场计算不正确。若在积分过程中，对不同深度采用不同的截止波数，可解决单向求解由核函数“发散”带来的问题。在Re(kr)>kmm区间内，正常情况下积分核函数绝对值应随Re(kr)的增加而减小，若在某一深度上积分核函数不断增加，则表明出现了“发散”，可在此“发散”的水平波数位置停止积分。采用该技术后，单向求解所得传播损失云图如图3(b)所示。

由于本算例有解析解，可以分析波数积分的数值误差。在不同深度上采用不同的截止波数后(图3(b)的状态)，单向求解的声压均方根误差为RMSP=2.67E-3、传播损失(TL=-20lg|P|, 单位dB)均方根误差为RMSTL=3.59E-2。

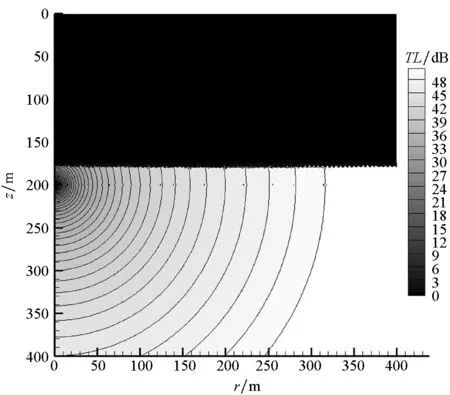
(a) 所有深度均采用相同的截止波数(a) Same truncate wavenumbers at different depths

(b) 不同深度采用不同的截止波数(b) Different truncate wavenumbers at different depths图3 球面波传播损失云图，单向求解(f=150 Hz)Fig.3 Acoustic transmission loss of free space spherical wave, bottom-to-top propagator(f=150 Hz)

2.2 双向求解

采用双向求解方法计算相同的算例，最大截止波数自动选取算法得到kmax=5.0k=3.14(取到了初始预估值)，积分核函数在各深度上均未出现“发散”现象，声场计算正确。声压均方根误差为RMSP=2.62E-3、传播损失均方根误差为RMSTL=3.36E-2。与单向求解法相比，双向求解法稳定性更好、数值误差更小。

3 结论

1)针对波数积分传递函数矩阵法计算不稳定的问题(出现NaN而崩溃)，提出了最大截止波数自动选取算法，可处理任意多层声介质，且具有简单可靠、附带计算量小的优点；

2)深度方程单向求解法在越过声源点深度继续向上传递的过程中，易出现积分核函数非物理发散(未出现NaN，但数值异常)，需要在不同深度上采用不同的截止波数才能积分出正确结果；

3)与单向求解法相比，双向求解法稳定性更好，数值误差更小。