平稳小波去噪算法中的参数选择*

张 恒，潘仲明

(1. 国防科技大学 前沿交叉学科学院， 湖南 长沙 410073; 2. 国防科技大学 智能科学学院， 湖南 长沙 410073)

传感器采集到的目标信号混有噪声，不能直接进行后续应用处理，在用采集到的目标信号做后续分析之前，应先对信号进行去噪处理。小波变换具有自动调整时域和频域分辨力的特点，在信号的奇异点监测、数据压缩以及信号去噪等领域有广泛的应用。小波去噪算法在对信号进行去噪处理时，首先对信号进行分解得到各层小波系数，然后对小波系数进行处理得到新的小波系数，最后进行小波重构得到去噪后的信号。在使用小波方法对信号去噪时，小波基、小波分解层数、阈值处理方法及其阈值的选取决定了去噪效果。

实际应用中，小波去噪算法对信号进行处理时，在不同领域均是针对本领域信号的特点来选择适合的小波基[1]。文献[1]从小波基的正交性、双正交性、紧支撑性和消失矩阶数出发，分析了常用小波的特性，其分析结果见表1。

表1 常用小波基特性比较

文献[2]从小波基的联合时-频分辨率特性出发，分析了常用小波基的时间、频率分辨率和时-频分辨率，用作选取小波基的参考。

这两种小波基的分析方法对于小波分析中小波基的选取有一定参考价值。但存在问题：从正交性、平滑性和紧支撑性等特征出发选择小波基，能有效平衡小波去噪算法的计算复杂度和高频细节分辨能力，但无法指导去噪算法选择去噪效果最好的小波基；从小波基函数的时-频分辨率出发，能选择出在时域和频域中更好辨别两个相邻信号成分的小波基函数，但无法增强噪声和信号在小波各层系数上的差异。

小波去噪算法中关于系数处理方法及对应阈值选取的研究已经较为成熟，常用的小波系数处理方法有模极大值法[3]、(软、硬)阈值法[4]以及空域相关法[5]，表2列出了文献[6-7]所总结的三种去噪方法的优缺点、运算量及适用情况。在使用阈值法处理小波系数时，阈值的选取直接决定了去噪的效果。

表2 常用小波系数处理方法比较

本文对比了平稳小波变换(Stationary Wavelet Transform，SWT)去噪算法使用不同参数时的去噪效果，对算法实现过程中如何选取滤波器组、小波系数处理方法以及对应阈值计算方法以获得最佳的去噪效果进行了研究，从而解决SWT去噪算法在实际应用中该如何选取参数的问题。

1 平稳小波变换

通常使用Mallat算法实现离散小波变换(Discrete Wavelet Transform,DWT)。Mallat算法[8]在输入信号与正交滤波器组卷积后，进行下采样得到小波系数。但因下采样运算使得DWT缺乏平移不变性，即将源信号平移后做离散小波变换，和先将源信号做离散小波变换再平移小波系数所得到的结果不同，导致使用DWT去噪算法对信号进行去噪时，信号截取的起始位置不同得到的结果也不同。SWT在计算每层小波系数时，信号与正交滤波器系数组卷积后不进行下采样，保证了小波变换的平移不变性。

Shen等利用z变换的等效易位性质，提出了在正交滤波器各点间插入一定数目的零点再做卷积运算的多孔算法[9]，通常使用它来实现SWT。图1所示为多孔算法的计算流程。对滤波器进行插零后用当前层输入信号与正交滤波器组做卷积，信号与分解高通滤波器系数卷积后得到小波细节系数，与低通滤波器系数卷积后得到小波近似系数，当前层的近似系数作为下一层的输入信号继续进行分解。重构过程则相反，当前层近似系数与重构低通滤波器卷积，细节系数与高通滤波器卷积，然后将卷积结果相加得到上一层近似系数。

图1 多孔算法分解和重构信号的流程Fig.1 Process of decomposing and reconstructing the signal using à trous algorithm

在多孔算法的分解和重构过程中，每一层滤波器系数都是在上一级的滤波器的相邻系数之间插入零值得到的新序列，即第j层的滤波器系数是在第1层滤波器的相邻系数之间插入2j-1个零后所得到的新滤波器系数。式(1)和式(2)为多孔算法的分解公式。

(1)

(2)

其中，cA0(k)等于初始信号序列x(k)，*表示卷积运算，K为信号序列长度，J为小波分解层数，S表示滤波器系数长度的一半。

式(3)为多孔算法的重构公式。

(3)

重构后的cA0(k)即为重构后的信号序列x′(k)。

2 平稳小波去噪算法中的参数

SWT去噪算法首先对信号进行小波分解得到一组小波系数，然后对这组系数进行处理得到新的小波系数，最后对新的小波系数进行小波重构得到去噪后的信号。在实际应用SWT去噪算法时，需要对算法中的正交滤波器组系数、小波系数处理方法(包括阈值处理方法及所用阈值)进行选择。

2.1 正交滤波器组系数选择

SWT去噪过程中，正交滤波器组的选择至关重要，一组合适的正交滤波器组系数，能在提高去噪效果的同时减小算法的运算量。对于小波去噪时滤波器组系数的选择，目前尚未有明确有效的结论，论文在第3节中对比了不同正交滤波器组的去噪效果并做出总结。

正交滤波器组系数一般由正交小波基推导得到，以实现信号序列的快速正交小波变换。常用的正交小波基，如Haar小波、Daubechies紧支集小波、Symlets小波的特点在表1中做了总结。除了小波基对应的正交滤波器，也可用一定的规则设计新的双正交滤波器，由新的双正交滤波器可以推导出新的小波正交基。文献[10]给出了设计接近于正交的双正交滤波器组的两种方法，一种是采用B样条函数按正规性条件[11]设计的数字滤波器组G0(z)和H0(z)，另外一种是接近正交的双正交滤波器。文献[10]中所列的采用B样条函数设计的双正交滤波器组按阶次的不同分别记为SP4和SP5。所列的接近正交的双正交滤波器系数按阶次记为BP2和BP3。

2.2 小波系数处理方法

小波系数处理是基于小波变换去噪方法的中间环节，决定算法的去噪性能。

常用的小波系数处理方法有以下几种：模极大值法；软、硬阈值处理法；空域相关法。文献[4]详细描述了小波系数的软、硬阈值法。文献[5]详细介绍了空域相关法的流程和参数选择。软、硬阈值处理法中对于阈值的选取有以下几种常用的方法：极大极小值法(minimaxi)[12]，启发式阈值法(heursure)[13]、无偏风险估计法(rigrsure)[14]、固定门限准则(sqtwolog)[15]。

3 仿真实验

3.1 评价指标

评价指标是分析小波去噪效果的基础，使用信噪比SNR以及平滑度R[16]作为去噪结果评价指标。

式(4)给出去噪信号的信噪比计算方法，去噪信号信噪比越大，说明去噪效果越好。

(4)

式中，y(k)为去噪后的新序列，s(k)为不含噪的信号序列。

平滑度能反映去噪后信号与原信号相比的平滑程度变化，其计算公式如式(5)所示。

(5)

R值越小，表明去噪后的信号越平滑；R值越接近于1，表明去噪后信号的起伏程度越接近于原不含噪信号的起伏程度。

3.2 不同正交滤波器组系数对去噪结果的影响

为对比不同小波基对应的正交滤波器组系数对信号去噪效果的影响，表3中给出使用不同滤波器组对信噪比为-7 dB的含噪重余弦波信号进行去噪处理后的信号信噪比及平滑度。

表3 不同正交滤波器组对含噪重余弦信号的去噪结果

选用不同的滤波器组对信噪比为-10～5 dB的重余弦波信号进行分解，使用软阈值法(阈值计算方法使用minimaxi)对小波系数进行处理。为排除随机干扰，使用不同滤波器组系数对每种信噪比条件下的信号进行去噪时，重复500次后求均值得到最后结果，含噪重余弦信号的去噪结果如图2所示。

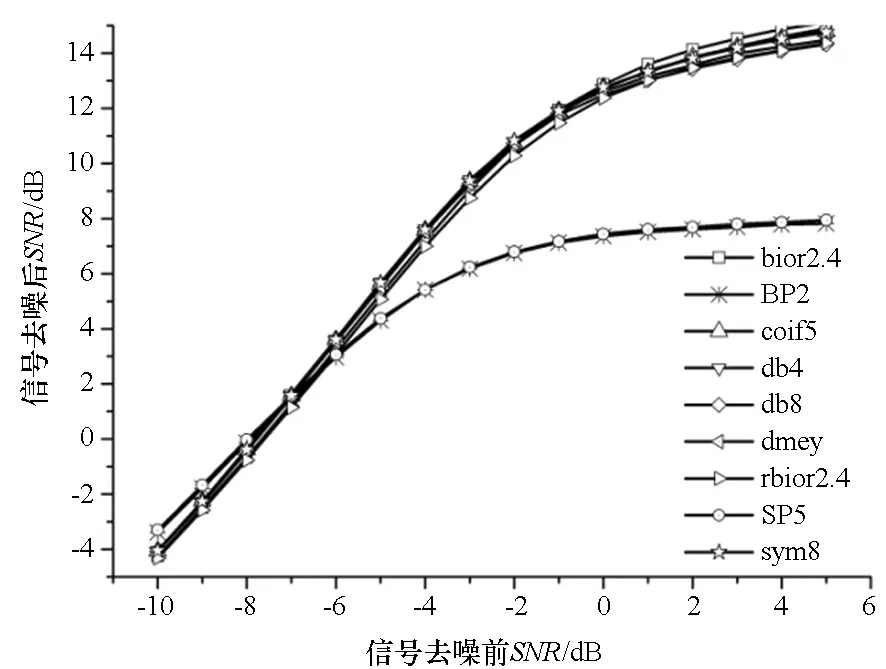
(a) 含噪重余弦信号去噪后的信噪比(a) SNR of the signal after denoising

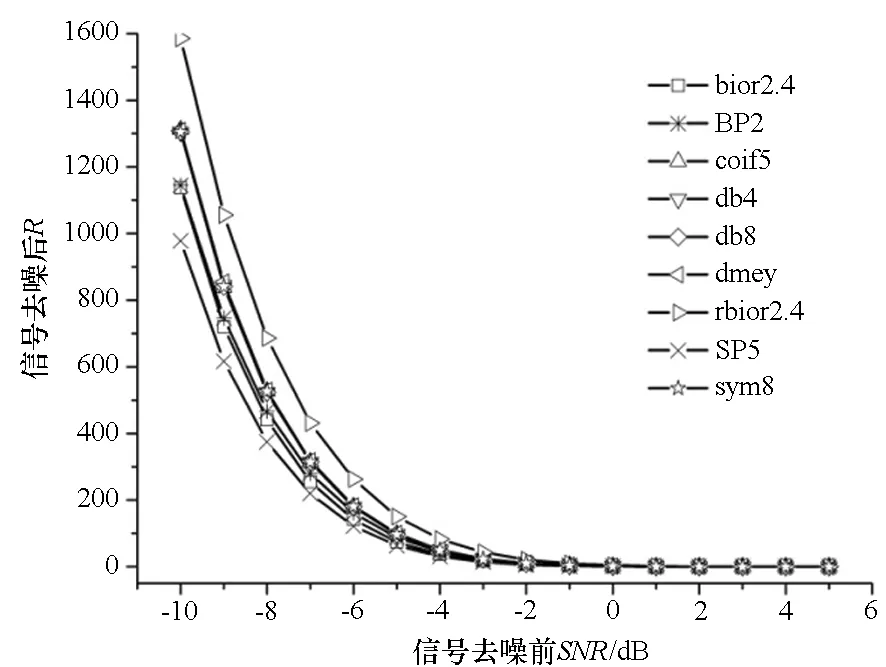
(b) 含噪重余弦信号去噪后的平滑度(b) Smoothness of the signal after denoising图2 不同正交滤波器组系数去噪效果对比Fig.2 Comparison of denoising performance of using different orthogonal filters

仿真结果表明：①使用Daubechies、Discrete Meyer、Coiflets、Symlets等小波基对应的正交滤波器组对信号去噪后得到的信号的信噪比差异较小，在图中表现为多个线条重叠在一起。②滤波器长度与去噪效果无关，如db4对应的滤波器长度是db8对应滤波器长度的一半，在大部分信噪比条件下，前者去噪效果十分相近。③在信号信噪比小于-6 dB时，两种根据一定规则设计的正交滤波器组BP2和SP5去噪效果优于Daubechies等小波基对应的正交滤波器组系数；在信噪比大于-5 dB时，Daubechies等小波基对应的正交滤波器组的去噪效果要优于所构造的BP2和SP5。

从表中所列数据可以看出，使用Daubechies 小波基对应的滤波器组对信号进行去噪后其信噪比更高。综合来讲，信号信噪比未知时，去噪时选用db4或者相近的小波函数对应的正交滤波器组能得到较好的去噪结果。

3.3 不同小波系数处理方法对去噪结果的影响

在对比不同小波系数处理方法对去噪结果的影响时，使用多孔算法对信噪比为-10～5 dB的含噪重余弦波信号进行分解后，选用所总结的四种不同小波处理方法(软阈值法、硬阈值法、空域相关法、模极大值法)对得到的小波系数进行处理，其中软阈值法和硬阈值法在选取阈值时都采用minimaxi。为排除随机干扰，重复仿真500次后求均值得到最后结果。含噪重余弦波信号去噪结果如图3所示。

仿真结果表明：①信号信噪比较小时，使用空域相关法得到的去噪信号信噪比接近使用软阈值方法得到的去噪信号信噪比；②在大部分信噪比条件下(-10～1 dB时)，软阈值去噪方法在四种系数处理方法中去噪效果最好；③在信噪比较高时，硬阈值法的去噪效果要优于其他三种方法；④软阈值法去噪后信号的平滑度最佳。

(a) 含噪重余弦信号去噪后的信噪比(a) SNR of the signal after denoising

(b) 含噪重余弦信号去噪后的平滑度(b) Smoothness of the signal after denoising图3 不同系数处理方法去噪效果对比Fig.3 Comparison of denoising performance of using different coefficients processing methods

表4给出了使用不同小波系数处理方法对信噪比为4 dB的含噪方波进行去噪处理后的信号信噪比及平滑度。从图3结果和表中数据可以看出，信噪比较高时使用软阈值方法对信号进行去噪，去噪后的信号会出现过平滑现象。

表4 不同系数处理方法对含噪重余弦信号的去噪结果Tab.4 Denoising performance of using different coefficients processing methods

3.4 不同阈值选取方法对信号去噪结果的影响

阈值选取是影响阈值法去噪效果的最重要因素。使用多孔算法对信噪比为-10～5 dB的含噪重余弦波信号进行分解重构后，选用软阈值法(软阈值法中的阈值选取方法分别使用rigrsure、heursure、sqtwolog及minimaxi)对得到的小波系数进行去噪处理。重复仿真500次后求均值得到最后结果，去噪结果如图4所示。

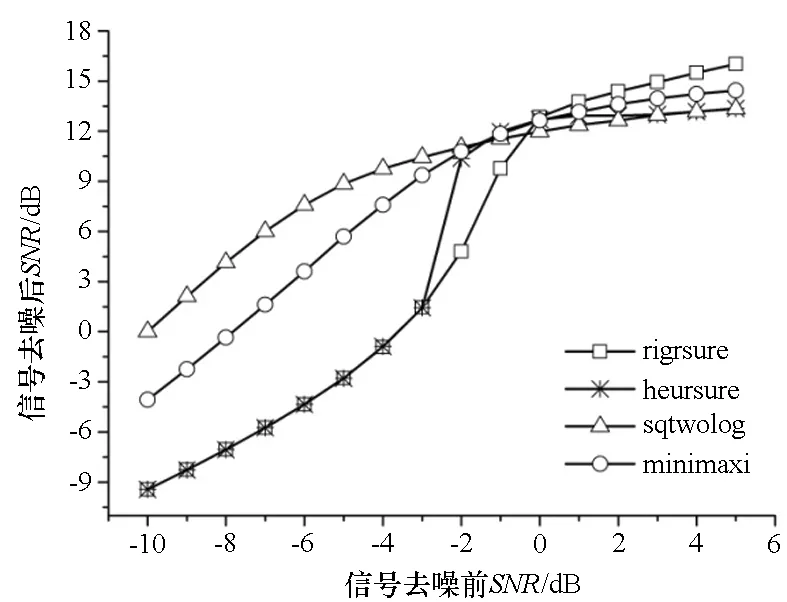
(a) 含噪重余弦信号去噪后的信噪比(a) SNR of the signal after denoising

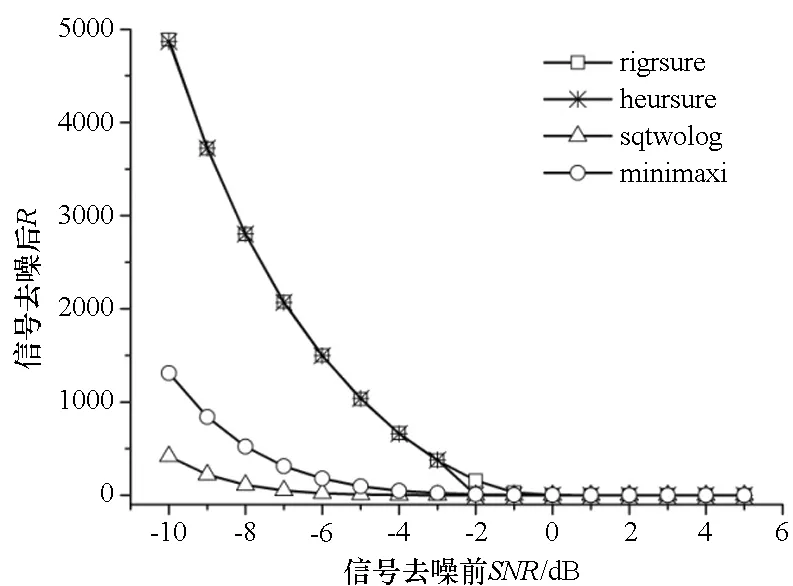
(b) 含噪重余弦信号去噪后的平滑度(b) Smoothness of the signal after denoising图4 软阈值法使用不同阈值选取方法去噪效果对比Fig.4 Comparison of denoising performance of using different threshold value calculation methods

仿真结果表明：①含噪信号信噪比不高的情况下，软阈值系数处理法使用sqtwolog来确定阈值时的去噪效果要优于其他几种阈值确定方法；②在信噪比较大的情况下，软阈值系数处理法使用rigrsure来确定阈值时的去噪效果最好；③软阈值法使用sqtwolog来计算阈值时，去噪后信号的平滑度最佳。

4 结论

本文通过仿真实验对比了SWT去噪方法中正交滤波器组、小波系数处理方法以及阈值计算方法对去噪效果的影响。结果表明在常用的小波正交滤波器组中，大部分情况下Daubechies 小波基对应的正交滤波器组去噪效果较好；小波系数处理方法应根据信号的信噪比选取，信号信噪比较低时选用软阈值法，信噪比较高时选择硬阈值法；使用阈值法处理小波系数，信号信噪比不高的情况下应采取固定阈值法来确定阈值，信号信噪比较高时应采取rigrsure。SWT去噪算法能显著提高含噪信号的信噪比，可以用于无人地面传感器系统中目标分类前的信号去噪。