相似分布特性准则下的高斯混合项聚类-合并算法*

徐 洋，方洋旺，伍友利，张丹旭

(空军工程大学 航空工程学院， 陕西 西安 710038)

在目标跟踪领域中，系统模型误差不可避免，产生的原因主要有目标运动状态的变化及目标运动模型的“双非”(非线性、非高斯性)问题[1]。解决上述问题的主要方法有：提高运动模型自适应能力，如自适应机动模型[2]；改进滤波算法性能，如粒子滤波器(Particle Filter, PF)[3]；增强跟踪模型的适用范围以解决“双非”问题，如高斯混合模型(Gaussian Mixture Model, GMM)[4]。由于自适应机动模型人为设定因素过多且适用性还有待检验，而PF算法计算复杂度过高，难以应用于战时平台，为此传统方法是引入GMM对“双非”系统下的目标状态进行估计。

GMM是单一高斯概率密度函数(Probability Density Function, PDF)的扩展，理论上它可以平滑地近似任意非线性函数[5]，但其本身仍存在不足：当动态方程的噪声项及初始状态中不止一个采用GMM表示时，算法的计算复杂度会呈指数级增长[6]。为此学者们分别从不同角度提出解决方案，这些方法大体可概括为以下两种：基于剪枝的删减策略与基于聚类的合并策略。

基于剪枝的删减策略即是基于某种测量准则剔除影响程度较低的混合项。其中最为简单的一种即为删掉具有较低权重的高斯混合项[7]，但该方法对于具有多峰分布的PDF近似效果并不佳[8]。为此文献[9]提出了一种基于KL(Kullback-Leibler )散度的剪枝方法。该方法在剪枝的同时依然可保留原分布峰值特征，避免了上述问题的发生。文献[6]更是直接利用初始状态筛选有效的噪声混合项，从源头降低了混合项数量。

基于聚类的合并策略即是基于某种距离标准将相似的混合项加以合并，该削减策略得到了广泛认可。文献[10]通过寻找混合项中两两之间具有最小KL散度的混合项，然后将其合并达到削减数量的目的。但该方法每合并一次都要重新搜索所有混合项，时效性较差。文献[11]在此基础上，又利用了聚类合并的思想，虽提高了精度，但算法复杂度仍很高。文献[12]更是对典型合并方法进行了系统性分析与比较。正是以上GMM削减方法的提出，使得GMM得以应用于众多领域[13-17]。

为了充分利用混合项自身的分布信息，简化整体运算流程，在保证精度的同时提高算法效率，本文提出了一种复杂度适中、近似效果较好的高斯聚类-合并方法。首先基于高斯混合项的后验分布特性及置信区间，建立相似分布特性准则，并采用扩展积分均方误差(Extended Integral Square Error，EISE)准则求解最优置信区间，完成对混合项的高斯聚类；然后针对各高斯簇间存在的交叉项复用问题，利用局部最近邻(Local Nearest Neighbor, LNN)思想将其重新分配；最后在各高斯簇中利用多元合并方法，减少下次迭代混合项数量。通过仿真分析了有效置信范围的可行域，缩窄了置信范围的搜索空间，并通过两个典型场景与基于数量限制的高斯混合项[7](Gaussian Mixture Reduction based on Pruning，GMRP)、Runnall[10]及基于聚类的高斯混合项削减方法[11](Gaussian Mixture Reduction based on Clustering,GMRC)进行了对比，验证了本文算法具有较高的效费比。

1 GMM及改进方法

设线性系统的状态方程及观测方程为

(1)

式中：k≤NK为时间序列，NK为序列长度；状态量xk∈Rmx，其中mx为x的维度，初始状态分布为p(x0)，转移概率p(xk|xk-1)满足马尔科夫过程。观测量zk∈Rmz，其中mz为观测量z的维度，p(zk|xk)为系统似然函数；k时刻状态量及观测量的集合分别为x0:k={x0,…,xk}及Zk={z0,…,zk}；uk及vk分别为状态噪声和观测噪声；F为状态转移矩阵，H为观测矩阵。

利用GMM表示的总体概率密度为

(2)

式中：N(x;μ(i),P(i))为多维高斯分布的PDF；N为GMM中混合项数量；ΩN代表均值、方差及权重的集合；ωi代表第i个正态分布的权值。 将初始状态、状态噪声及测量噪声中的两个或三个用GMM加以表示，会导致在状态更新及时间更新阶段，系统的高斯混合项呈现指数级增长。 针对该点不足，在综合考虑高斯混合项权重信息和分布特性的基础上，本文提出如下基于相似分布特性准则的聚类-合并方法以动态削减高斯混合项。

2 混合项聚类-合并算法

2.1 高斯聚类

服从高斯分布的混合项之间无法定义为完全独立，而且聚类问题本身在统计上也是无法识别的[18]，因此每种聚类方法都包含着主观的聚类概念。 本文所提的高斯聚类方法是以混合项具有较小方差[18]为前提，依据相似分布特性准则加以聚类。 若混合项中存有较大方差项，可通过设置阈值δ将其排除在聚类项之外。 其中对于聚类依据——相似分布特性准则的定义如下：若p个具有较小方差的混合项的分布中心相互处于对方的P*置信范围内，则认为这些混合项在分布上具有P*相似特性，从而将其归为P*置信范围下的同一高斯簇。 该准则的现实意义即是：若高斯混合项之间分布形状足够相似、分布中心足够接近，则其合并后的PDF将服从单峰分布，且总体分布特性服从类高斯分布[19]。 为了搜寻可同属一个高斯簇的混合项，定义k时刻高斯混合项的分布中心向量Π为

(3)

定义如式(4)所示判别矩阵R用以判断混合项之间的相似性。

(4)

其中，

(5)

为了快速完成聚类，首先按行搜索判别矩阵，并对每个混合项附上隶属簇标签

(6)

步骤1：将交叉的高斯簇分成以下两种

(7)

步骤2：重新分配交叉项。

1)H1:将交叉项依LNN思想重新分配。 其过程如下：

(8)

②计算交叉项与所属高斯簇间距离

(9)

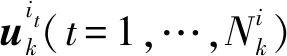
④重复步骤①～③直至交叉项分配完。

由上述可知：P*对于聚类结果影响很大。 若P*过大，则可能使得不具有相似分布特性的混合项归并为同一簇，使得混合项发生多样性退化，最终导致近似多峰分布时效果变差；若P*过小，则会使得聚类过细，无法明显减少高斯混合项个数而使得实效性达不到要求。 因此合理地选择P*对于提高算法的效费比尤为重要。 为此，本文提出基于EISE代价函数求解P*。

2.2 基于EISE函数的置信范围搜寻算法

为了筛选合适的P*，本文受文献[20]中所提ISE函数启发，通过增加正则化项，在限定高斯簇个数的同时使得近似误差逐渐降低，得式(10)所示EISE函数。

(10)

=Jhh-2Jhr+Jrr

(11)

其中，

式(11)两个高斯PDF可表示为

(12)

将式(12)代入到式(11)中，可得

(13)

两个高斯PDF的乘积可以简化为

N{x;u1,P1}·N{x;u2,P2}=αN{x;u3,P3}

(14)

其中，

α=N{u1;u2,P1+P2}

将式(14)代入式(13)，又因高斯子项的积分是在整个输入空间，故其积分结果为1，则最后只剩α。 则式(13)可表示为

(15)

至此，代价函数等于高斯簇中混合项之间的乘积加上每一个混合项与合并后项的乘积，加上合并后混合项的概率平方，再加上一个关于高斯簇数量的惩罚函数。因高斯簇已将全部混合项划分为多个高斯簇，而高斯簇内混合项数量也随着P*而变化——P*越小，混合项数量越少，这对于算法效率的提高是有帮助的，但同时也使得惩罚项变大。为了更有效地寻找最优解，可先缩小搜索域后利用MATLAB自带函数fmincon求解。

2.3 无偏多元素合并算法

为了降低聚类复杂度，在获得混合项后可剔除掉连续两步权值都非常小的混合项，此处可设阈值为0.01。之后基于文献[20]提出的合并方法，在保证系统状态无偏的前提下，对各高斯簇内的混合项进行合并

(16)

(17)

(18)

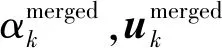
该融合方法可以保持原混合高斯项的中心矩不变[20]，而且计算方便，被大多数基于合并思想的改进方法采用[8,10-11]。

3 算法分析

3.1 算法流程

为了清晰算法步骤，下文中用GMM分别表示初始状态、系统噪声及观测噪声，并采用卡尔曼滤波方法对目标状态进行估计，具体算法流程可参考算法1。

算法1 聚类-合并算法

3.2 算法复杂度

在时间复杂度上，所提算法首先需要判断混合项之间是否具有相似分布特性，即计算判别矩阵。而判别矩阵只需得知上三角的值即可判别所有混合项间的相似关系，故第一步的时间复杂度为O(n2)；第二步因交叉项自带标签，故查找交叉项并不会占用时间，但在重新分配时需判断其与各所属簇间的最小距离，因此时间复杂度为O(n2)；第三步因采用多元素融合方法，其时间复杂度为O(lgn)；第四步为对置信范围采用非线性优化方法寻优，其时间复杂度为O(m×p×n2)，其中m为算法迭代次数，p为搜索粒子数量。由此可见，用于搜索的时间复杂度受代价函数性能、粒子初始状态及数量的影响，并且随着状态维度的升高，用于搜索最优P*值的迭代次数会呈指数级增加。因此所提算法更适用于低维度的状态。而为了限制该步骤的时间复杂度，有效合理地缩窄搜索范围至关重要。

针对空间复杂度，因算法需要空间存储融合后的混合项、高斯簇，故其空间复杂度为O(n)。标准算法因在迭代过程中需要大量空间来存储中间变量，并且每次采样混合项数量呈指数式增长，所以在空间复杂度上，改进算法具有明显优势。

4 性能分析

为了验证算法的有效性，首先利用三种典型场景来确定置信范围的有效搜索域，从而提高算法的搜索效率。同时为了方便图形呈现，选取一维情况加以说明。最后，针对二种常见的目标运动场景对运动目标的状态进行估计，以均方根误差(Root Mean Square Error, RMSE)作为评价跟踪性能的依据，并以中央处理单元(Central Processing Unit,CPU)运行时间作为评价时间复杂度的标准。

4.1 置信范围有效区间

4.1.1 四混合项呈单峰分布情况

四个混合项的参数分别设置如下：

Ω1(1)={0.3,N(x;1,12)}

Ω1(2)={0.1,N(x;1.5,1.22)}

Ω1(3)={0.4,N(x;2,0.52)}

Ω1(4)={0.2,N(x;3,0.82)}

令P*分别为1σ,2σ,3σ,4σ时，PDF近似效果如图1所示。由图可知，P*在1σ～3σ时算法对单峰PDF近似效果较好，而在P*=4σ时效果明显变差。这主要是因为当P*选择过大时，无法等效成单峰分布的混合项被归并成一簇，从而导致混合项多样性退化，导致近似精度下降。

图1 近似单峰PDFFig.1 Approximated PDF to single peak

表1为不同P*下算法效率。由表可知，当P*取2σ和3σ时近似效果几乎相同，这说明单纯的增加或减小P*并不一定能够改善近似效果，这与当前混合项的分布特性有关。并且，随着P*的增大，最终的混合项个数将呈下降趋势。

表1 单峰PDF下算法效率

4.1.2 四混合项呈双峰分布情况

四个高斯混合项的参数设置如下所示：

Ω2(1)={0.3,N(x;0.5,12)}

Ω2(2)={0.1,N(x;2,1.22)}

Ω2(3)={0.4,N(x;3.5,0.52)}

Ω2(4)={0.2,N(x;4,0.82)}

图2为置信范围分别为1σ、2σ、3σ及4σ时对应的PDF曲线。由图可以看出PDF的近似效果随着置信范围的增加而逐渐变差。当P*=3σ或P*=4σ时，近似效果不佳，尤其在峰值处。

图2 近似双峰PDFFig.2 Approximated PDF to double peak

该情况下算法效率如表2所示。由表可知，在近似具有双峰分布的PDF时，算法在降低高斯项个数方面性能较好，当P*=4σ时，其返回的高斯项个数仅为初始输入的一半，但耗时最长。

表2 双峰下PDF算法效率

4.1.3 八混合项呈多峰分布情况

八个混合项的参数设置如下：

Ω3(1)={0.1,N(x;0.5,1)}

Ω3(2)={0.05,N(x;2,1.22)}

Ω3(3)={0.35,N(x;3.5,0.52)}

Ω3(4)={0.1,N(x;4,0.82)}

Ω3(5)={0.1,N(x;5,0.22)}

Ω3(6)={0.2,N(x;-1,0.32)}

Ω3(7)={0.04,N(x;0,42)}

Ω3(8)={0.06,N(x;1,32)}

图3为不同置信范围P*下对应的近似PDF。由图可知在近似多峰分布的PDF时，改进算法的整体近似效果较为理想，但随着P*的增大，对于起伏处的PDF近似效果逐渐变差。算法效率如表3所示。

图3 近似多峰PDFFig.3 Approximated PDF with multiple peaks

由表3可以看出，P*的增加使得耗时也稍有增加，但同时获得的高斯混合项的个数也在减少，这更有利于用在递推算法中。

通过分析上述三种典型情况，可知过大的P*会使得近似精度变差，尽管可以大幅度降低输出的混合项个数、节省GMM迭代时间，但相应会增加聚类-合并的处理时间。

表3 多峰PDF下算法效率

在通过EISE代价函数计算的最优置信范围下，三种典型情况的近似性能如表4所示。

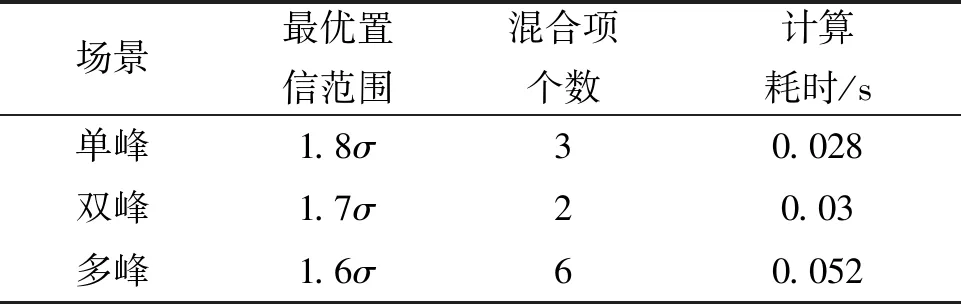
表4 最优置信范围下近似效果

通过上面三个典型的场景，将置信范围P*的搜索域设定在[0.5σ,3σ]以提高算法效率。

4.2 跟踪性能

在雷达接收系统中，因目标的散射特性使观测噪声也可能呈现非高斯性质，称之为闪烁噪声[21]。不同于高斯噪声，闪烁噪声尾部较长，而在中心区域则类似高斯形状。其概率分布可表示为

ft=(1-ε)fg+εfl

(19)

式中，ft,fg及fl分别代表闪烁噪声、高斯噪声及拉普拉斯噪声的分布，其表达式分别为

(20)

(21)

其中：xs表示特征变量；ε为一个小于1的小正数，其表示为闪烁频率，下文设ε=0.01；fg的方差σ小于fl的方差η。

其中参量的设定为：系统状态噪声的方差Q=diag[10,4,2]，x1=[30,20,10]T,P1=diag[300,100,50]，x2=[20,10,5]T,P2=diag[350,200,40]，v1=[10,5,2]T,R1=diag[100,25,4]，v2=[-10,3,1]T,R2=diag[100,9,1]。

4.2.1 圆周运动场景

在弱机动场景下，目标以0.02π rad/s的角速度作匀速圆周运动，其在100 s以内位置RMSE的对比如图4所示。

图4 位置RMSEFig.4 Position RMSE

图4中GMRC、Runnall、GMRCM、GMRP四种算法的平均位置RMSE分别为8.96 m, 9.29 m, 9.32 m以及9.78 m，由此可以看出对于弱机动目标，GMRC算法的跟踪精度最好，其次Runnall与本文提出的GMRCM算法精度相当，而GMRP算法的精度最差。在第50 s时刻目标状态的后验分布及混合高斯近似的后验分布如图5所示。

图5 目标状态后验分布Fig.5 Posterior distribution of target state

由图5可知，因多模型及非高斯噪声的存在，估计的位置后验概率密度函数呈现非高斯性质。各算法对于圆周运动的位置估计精度较为理想，其偏差幅度并不大。其中GMRC、Runnall以及GMRCM算法的估计精度相当，略优于GMRP算法。

置信范围P*随时间的变化情况如图6所示。

图6 最优置信范围的变化Fig.6 Variation of the confidence interval

由图6可知，针对弱机动情况下，P*大部分情况处于0.5～1.5P(1，1)之间(对应图中4～14 m)，即说明了在目标状态不发生突变的情况下，一般会取较大置信范围值，这主要是由于当前目标的状态后验分布比较均匀，具有多峰分布的情况并不多才使得P*较大。而P*会发生不断的跳动主要是由初始搜索点选择的随机性以及存在多个最优解造成的。

图7为间隔10个采样时刻的高斯混合项个数的变化情况。

图7 高斯混合项个数Fig.7 Number of Gaussian components

由图7知，改进算法所得高斯混合项个数要明显少于另外三种算法，这主要是由于GMRP算法与Runnall算法都是达到人为设定数量后才停止合并，而GMRC算法则还需要进行聚类操作，其数量会少于Runnall算法，但其用时则会受到影响。

针对算法的时间复杂性，分别记录了GMRC、GMRP、GMRCM、Runnall这四种算法的运行时长，分别为0.52 s, 0.44 s, 0.38 s, 0.48 s。由此可看出本文算法由于高效的搜索方法，迭代过程中的高斯混合项数量少，耗时最短。而GMRP算法由于在删除混合项过程中用时极短，即便在迭代过程中会耗时较长，但仍取得了较优的时间复杂度；GMRC算法由于计算最为复杂，故其用在筛选合并项过程中耗时最长，时间复杂度较高；Runnall算法因寻找合并项相对简单，故时间复杂度稍好于GMRC算法。

由上述分析可知，本文所提算法虽然在近似精度上不如GMRC算法，但能够达到与Runnall算法相当的精度，并且要明显强于GMRP算法。同时，在时间复杂度上，所提算法在对比算法中效率是最高的。

4.2.2 阶跃机动场景

该场景下目标机动较强，加速度变化情况为

图8 位置RMSEFig.8 Position RMSE

位置RMSE的对比情况如图8所示。针对阶跃机动情况，各算法平均位置RMSE为：GMRC为9.32 m、Runnall为9.58 m、GMRCM为10.2 m、GMRP为12.17 m。由此可知，虽然所提GMRCM算法的跟踪精度要明显好于GMRP算法，但相较于另两个算法，尤其在目标发生阶跃运动时间段内，跟踪精度仍有待提高。

第50 s处目标状态后验分布如图9所示。由图可知，因目标发生突变机动导致两个模型的滤波状态发生差异，使得模型的状态后验分布呈现双峰分布。从各算法近似曲线不难看出GMM可较好地近似出非高斯分布特性，但因状态的突变导致高斯混合子滤波器的滤波精度下降，PDF逼近程度并不高。但从位置RMSE曲线可以看出，精度仍可满足要求，并且GMRC与Runnall的近似精度较高，GMRCM次之，而GMRP最差。

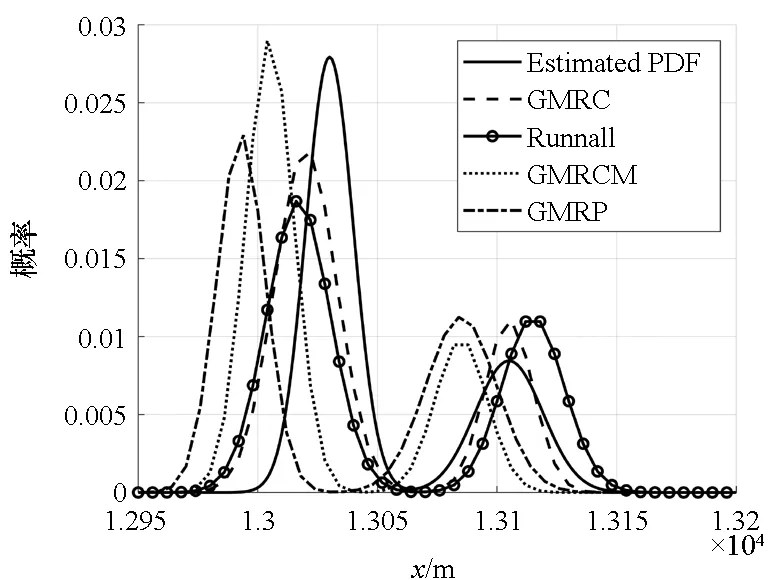
图9 目标状态后验分布Fig.9 Posterior distribution of target state

P*变化情况如图10所示。由图可以看出，当目标发生阶跃机动时，GMRCM算法的最优置信范围会变小以适应状态的突变，进而获得较优的跟踪性能。而对于目标运动平缓阶段，最优置信范围则会增大来适应稳定的状态后验分布。

图10 最优置信范围的变化Fig.10 Change of the confidence interval

采样点处的混合项个数如图11所示。图中本文所提算法GMRCM的高斯混合项个数要少于其他三种算法。尽管当目标发生阶跃机动时，目标的高斯项个数还是会增加，这主要是由于机动时刻目标状态的后验分布呈多峰形式，使得高斯簇增加进而增多了数量，但同比于其他三种算法，仍有优势。

图11 高斯混合项个数Fig.11 Number of Gaussian components

针对算法的时间复杂性，GMRC、Runnall、GMRCM、GMRP四种算法的计算耗时分别为0.67 s, 0.57 s, 0.45 s, 0.62 s。由此可见针对阶跃机动情况本文算法可以获得较高的跟踪效率。

由以上分析可知，在跟踪阶跃机动目标时，本文所提算法在跟踪精度上较之GMRC、Runnall算法稍有不足，但仍在可接受范围内。并且，本文算法的效率在四种对比算法中是最优的。

5 结论

针对GMM估计非高斯系统状态时会导致高斯混合项个数呈指数级增长问题，本文基于相似分布特性准则，提出了一种混合聚类-合并方法。通过定义相似分布特性准则，基于EISE代价函数寻求最优置信区间以对混合项进行高斯聚类，建立具有不同分布特性的高斯簇。为了解决各高斯簇中的交叉项的复用问题，引入LNN思想对交叉项重新分配。为了削减迭代过程中混合项数量，采用并行多元素融合法将高斯簇内的混合项合并。最后通过仿真验证了算法在保持跟踪精度及提高运算效率方面的有效性。