基于不完全双列杂交设计的水稻农艺性状配合力基因组预测
王欣 马莹 胡中立 徐辰武,
基于不完全双列杂交设计的水稻农艺性状配合力基因组预测
王欣1,2,3马莹1胡中立3徐辰武1,*
(1江苏省作物遗传生理重点实验室/植物功能基因组学教育部重点实验室/江苏省作物基因组学和分子育种重点实验室/扬州大学 农学院,江苏 扬州,225009;2扬州大学 信息工程学院,江苏 扬州 225009;3杂交水稻国家重点实验室/武汉大学 生命科学院,武汉 430072;*通讯联系人, E-mail:cwxu@yzu.edu.cn)
【】在亲本一般配合力的基础上优选特殊配合力高的杂交种,是水稻杂种育种的关键。基因组选择基于覆盖全基因组的分子标记和样本的表型数据建立预测模型,实现对品种更加可靠的选择。本研究利用一组基于不完全双列杂交(NCII设计)的水稻数据集,考查其多个农艺性状配合力的基因组预测能力。并比较了不同训练群体构建方法对杂交种表型预测能力的影响。8个农艺性状一般配合力的预测能力由其遗传率主导,从0.3888到0.7367。杂交种特殊配合力的预测能力较低,但是直接预测杂交种的表型可以获得较高的预测能力。基因组预测水稻亲本一般配合力是有效的,能够帮助育种家实现对亲本的科学选择。如果要选配杂交种,直接预测杂交种表型是最有效的手段。此时让更多的亲本均衡地参与杂交种训练集的组配,有利于获得更高的预测能力。
水稻;不完全双列杂交;表型;配合力;基因组预测
杂种优势的利用,对水稻的育种工作至关重要。基因组选择(genomic selection,GS)[1]基于覆盖全基因组的分子标记和样本的表型数据建立预测模型,实现对品种更加可靠的选择。分子辅助育种技术的发展,为降低育种盲目性,提高水稻育种效率,提供了一些新的方法。如近年流行的分子辅助选择育种[2],已经在水稻等作物育种领域得到广泛的应用。但是分子辅助选择育种只适合导入和聚合少数主效位点,目前主要应用于抗病、抗虫等单基因遗传性状的改良。基因组选择在全基因组范围内同时估计出所有标记的效应,高密度的标记覆盖整个基因组,一些标记与QTL很近,并与其处于连锁不平衡,全基因组的大量标记信息就可能解释所有的遗传方差[3]。研究表明,用高密度分子标记预测遗传效应更加精确[4-5],它为水稻等作物的育种工作提供了新的参考。
在水稻的杂种育种工作中,由于亲本组合的多样性,要进行完全双列杂交是困难的。不完全双列杂交设计(NCⅡ设计)则是杂种育种中更加可行的方案,它在一定的试验规模下,利用到较多的亲本资源[6]。要衡量亲本材料在杂种优势利用或杂交育种中的利用价值,一般配合力(GCA)和特殊配合力(SCA)是最常用的评价标准。GCA是指一个自交系亲本与其他若干个自交系杂交的F1在某个数量性状上的平均表现,SCA是指两个特定亲本所组配F1在某种数量性状上的表现。在亲本GCA的基础上优选较高SCA的杂交种,是水稻杂种育种的关键。玉米的GCA已经通过基因组选择方法得到了较好的预测。Riedelsheimer等[7]用570份玉米杂交种的基因型和表型数据,预测了7个性状的GCA,准确性达到0.72~0.81。不过利用基因组选择方法预测水稻农艺性状GCA和SCA的研究却鲜见报道。本研究的主要目标是考查基因组选择方法对于NCⅡ设计下水稻亲本GCA和杂交种SCA的预测能力,并探讨不同训练群体构建方法对杂交种表型预测能力的影响,以更好地指导水稻杂交种的基因组选择育种工作。
虽然利用基因组选择(GS)可以有效预测表型未知群体的遗传效应,但是已有的GS方法大多只针对最简单的加性效应进行估计,而忽略其他遗传效应[8]。杂交水稻的实际遗传组成是复杂多样的,同一位点内不同等位基因间的相互作用构成了显性效应,一些研究表明显性效应是产生杂种优势的主要因素,其贡献超过了其他各种效应[9]。在模型中引入显性效应可能有助于解析复杂性状的遗传组成[10],但是显性效应在经典的GS研究中经常被忽略。解析各种农艺性状的遗传方差,研究显性效应与加性效应的关系以及显性离差对育种值估计的影响有着十分重要的意义[11-13]。本研究所使用的数据集是NCⅡ设计下的水稻杂交种,因而有必要建立加-显模型开展预测工作。
1 材料与方法
1.1 材料来源
本研究使用的水稻数据集[14]来自武汉大学。基于NCⅡ设计,115个水稻自交系与5个不育系(包括新安S、珞红3A、Y58S、广占63S和PA64S)杂交,575个杂交种和115个水稻亲本自交系的表型数据,包括单株产量(GY)、千粒重(TGW)、有效穗数(PN)、株高(PH)、一次枝梗数(PB)、二次枝梗数(SB)、主穗实粒数(GN)和穗长(PL)等8个农艺性状。该数据集于2013年在华中农业大学和湖北省农业科学院鉴定,每个环境下两次重复。本研究模型中使用到的水稻表型数据是两个环境下两次重复的平均值,基因型信息是亲本全基因组上3 299 150个SNP标记。
1.2 方法
1.2.1 模型与算法

=+++;1)
其中,为表型或配合力向量,是非遗传的固定效应,和分别为加性和显性效应,为残差。是固定效应的关联矩阵,是×的随机效应关联矩阵(是训练群体中个体的数目,是整个群体中个体的数目)。
G=MM′/a; 2)

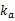
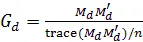

各种效应所解释的方差比例是重要参数,本研究使用限制性极大似然估计(REML)方法进行估计。首先用快速的AI-REML算法[20, 21]进行参数的非线性寻优,然后以更加稳健的EM算法[10]作为补充,如果相邻两轮迭代的方差比例之差小于10−6,则视为收敛。本研究中的模型与算法皆使用R语言实现[14]。
1.2.2 一般配合力的预测方法
本研究所使用NCⅡ水稻群体的母本不育系和父本差异较大,所以只针对父本的GCA进行了预测,这里考虑的遗传效应只包括加性效应,即忽略式1)中的项,模型称为GBLUP-A。除了完全随机的20次5倍交叉验证,还尝试使用留一法(每次抽取114个父本作为训练集来预测剩余的1个父本)考查模型的效果。
1.2.3 特殊配合力的预测方法
115个父本和5个母本组配得到575个杂交种,SCA数据是575维的向量,本研究采用20次完全随机的5倍交叉验证方法,每次对随机抽取的115个杂交种SCA所构成的测试集进行预测。预测时共采用了两种方案。第一种是考虑模型=+ Za+ Za++,其中为杂交种表型向量,是非遗传的固定效应,a和a分别为父本和母本的GCA,为杂交种的SCA,为残差。通过对进行估计来预测115个杂交种的SCA,称为SCA方法1。第二种方案则首先用式1)中的加-显模型(称为GBLUP-AD)对随机选取的115个杂交种的表型进行预测,然后将其预测值与460个杂交种的真实表型值相结合,估算115个杂交种的SCA,称为SCA方法2。
1.2.4 杂交种训练群体的构建方案
除了对配合力的预测,本研究还考查了不同训练群体构建方法对杂交种表型预测能力的影响。对于575个杂交种,交叉验证时首先进行完全随机分组,如图1-A所示,这一分组方案的训练集和测试集是完全随机产生的,反映的是该数据集平均的预测能力。除了完全随机分组,本研究还考查了均匀随机分组(每个杂交种测试集的亲本都覆盖全部115个父本1次,并覆盖5个母本各23次,其余杂交种为训练集,如图1-B),只针对115个父本自交系进行的横向随机分组(每个杂交种测试集的亲本都覆盖23个父本各5次,覆盖5个母本各23次,如图1-C),和只针对5个母本不育系进行的纵向分组情况(每个杂交种测试集的亲本都覆盖全部115个父本1次,覆盖1个母本115次,如图1-D)。
1.2.5 预测能力的衡量
本研究采用交叉验证的方法考查预测的效果。对于GCA、SCA和表型值,本研究计算测试集真实值和预测值之间的相关系数,并对多次不同交叉验证的结果进行算术平均,以衡量模型的预测能力。对于亲本表型和GCA的留一法,则将115次预测所得到的估计值组成一个向量,计算与真实表型向量或GCA向量的相关系数,得到模型的预测能力。
2 结果与分析
2.1 亲本一般配合力的预测
根据GCA可以选择优异的亲本。本研究将115个亲本各个农艺性状的GCA看做因变量,其平均预测能力见表1。结果显示,8个农艺性状GCA的预测都是有效的,单株产量的预测能力最低(0.3888),千粒重和株高的预测能力最高(分别为0.7367和0.6112)。结合表1中列出的各性状遗传率(由REML估计),说明性状的遗传率是决定其GCA预测能力的主要因素。另外,从表1中可以看出,留一法和5倍交叉验证的预测能力大体在同一水平,说明训练集个体数目从92增加到114,并未给亲本GCA的预测能力带来显著的改善。

图1 交叉验证分组方案
Fig. 1. Grouping schematic diagram for cross- validation.
2.2 杂交种特殊配合力的预测
由于杂交种的SCA不仅与其基因型有关,还与双亲的基因型有关,所以不宜将SCA看作因变量,直接用杂交种的基因型进行预测。本研究采用两种方法对杂交种的SCA进行了预测(表2),发现方法2的预测能力显著高于方法1,在预测SCA时更具优势,不过其水平仍然大幅低于亲本一般配合力的预测能力。另外,使用SCA方法2时,遗传率较高的性状未能获得较高的预测能力,原因可能在于特殊配合力理论上与加性效应无关,完全由非加性效应所决定。REML结果显示,8个性状的显性方差占表型方法的比例从0.41%到7.89%,平均仅3.20%,加性方差占表型方法的比例从36.72%到82.34%,平均达到64.61%,即该NCⅡ水稻杂交种的农艺性状主要由加性效应控制。由于非加性效应占比较低,影响了SCA的预测精度,也使得遗传率较高的性状未能获得较高的SCA预测能力。

表1 各性状遗传率和亲本自交系GCA的平均预测能力

表2 杂交种SCA的平均预测能力

表3 不同分组情况下杂交种的平均预测能力
2.3 不同训练群体构建方法对杂交种表型预测能力的影响
本研究使用GBLUP-AD模型,考查了不同训练群体构建方法对杂交种表型预测能力的影响。各种不同分组情况下杂交种的平均预测能力见表3。结果显示无论采用哪种分组方案,单株产量的预测能力最低,千粒重和株高的预测能力最高,这一点与前面GCA的预测结果一致。
值得注意的是,均匀随机分组下所有性状的预测能力都优于完全随机分组,原因可能在于均匀随机分组时训练集和测试集的亲本分布比完全随机分组更加均衡,使得训练集和测试集的平均遗传相关程度最大化,从而有利于提高模型预测能力。几种分组方案里,横向随机分组的预测能力最低,此时测试集的父本都未参与训练集的杂交,这种情形下测试集父本的后代表型信息完全缺失,可能影响不同父本后代表型相对优劣的判断,给预测的精度带来负面效应。对于大部分性状,纵向分组的情况与完全随机分组相近,比横向随机分组要好得多,此时虽然测试集母本的后代表型信息完全缺失,但是由于整个测试集的母本相同,其表型差异主要取决于父本,而父本的遗传信息在训练集中是充分的,因此不会影响后代表型相对优劣的判断,所以预测能力与完全随机分组水平相当。综上所述,均匀随机分组的预测效果最好,表明在利用GS方法开展水稻杂种育种时,应尽可能让更多的亲本均衡地参与杂交种训练集的组配,以获取较高的预测能力。
对比前面的研究结果不难发现,要实现对杂交种的科学选配,直接预测杂交种表型是最有效的方法,此时让更多的亲本均衡地参与杂交种训练集的组配,有利于获得更高的预测能力。然而亲本改造也是杂种育种中的重要工作,在这一过程中经常需要对具有较高GCA的亲本进行连续杂交,所以对亲本GCA的预测也是十分重要的手段。
3 讨论
3.1 遗传率对预测能力的影响
GBLUP-A模型不仅可以用来预测亲本的GCA(表2),还可以预测亲本的表型(表4)。无论是5倍交叉验证还是留一法,二者的预测能力总体上较为接近。另一方面,8个性状亲本表型和GCA之间的相关系数见表5,表中第二列为亲本所观测的表型值和根据NCII设计计算出的GCA之间的相关系数。第三列为利用GBLUP-A得到的亲本表型预测值和GCA预测值之间的平均相关系数。可以看到,无论对于实际值还是模型的预测值,亲本表型和GCA之间都存在较强的相关性,而且两组相关系数基本处于同一水平,这些都与加性效应决定亲本表型和GCA的理论相一致。

表4 亲本自交系表型的平均预测能力

表5 亲本表型与GCA的实际值相关系数和预测值相关系数
本研究所预测的NCⅡ水稻群体,无论亲本表型和GCA,还是杂交种的表型,8个性状中单株产量的预测能力都最低,千粒重则最高,这一结果显然由性状的遗传率所决定。在前人所研究的其他群体中,也有类似的情况。Xu等[22]在210份水稻重组自交系亲本衍生的21 945份杂交后代中随机选择278份材料进行表型鉴定,并预测了四个性状,发现产量的预测力最低,只有0.13,而千粒重的预测力最高,达到0.68。Wang等[15]用模拟手段考查多种GS模型的预测效果,指出遗传率是影响预测精度的最主要因素。产量性状是育种家最为关心的性状之一,然而它的遗传率较低,容易受到多种环境因素的影响。不过较低的预测能力并不代表对产量性状的预测是无效的。有研究表明,利用GS方法对低遗传率性状进行优选,其结果可能具有较大的标准差,适当提高优选群体的数目,就能降低这种波动,获得相对稳定的平均选择优势[14]。千粒重等性状的预测能力较高,虽然它们不是育种家关注的焦点,但是这些高遗传率性状可以用来进行辅助预测,以提高产量等低遗传率性状的预测精度[6]。另一方面,千粒重等性状具有较高的预测能力,可以用来考查模型在不同条件下的预测差异,如Dan等[23]近期就利用千粒重研究不同条件下代谢物预测水稻杂交种表型的效果。
3.2 训练群体大小和亲缘关系对预测能力的影响
对于本研究中的大部分性状,亲本表型和GCA的预测能力要远低于杂交种表型的预测,这里最重要的因素可能是训练群体的大小。一般来说,较大的训练群体能够提供较高的预测精度,因为具有表型和基因型信息的样本越多,所提供的信息就越丰富,从而能够提高等位基因效应估计的准确性,进而提高GS的准确性[24, 25]。据van Raden等[26]报道,训练集数目分别为1151、2130、2609和3576时,预测产奶量的决定系数分别为0.12、0.17、0.21和0.28,随着个体数量的增多几乎呈线性增长。Wang等[14]的研究中,训练集的个体数目从539降到300时,5种不同GS模型的平均决定系数从0.259降到0.206。本研究中亲本表型和GCA在完全随机交叉验证时,训练集个体数目仅为92,而杂交种表型预测时训练集个体数目为460,训练群体巨大的差异显然是不可忽略的因素。
另外,训练群体和测试群体的遗传关系会影响预测的精度[27],对于遗传上相似的群体往往能够获得较高的预测准确性[3]。Riedelsheimer等[28]的研究表明,在玉米双亲杂交群体的训练集中增加来自双亲的半同胞家系材料,与随机增加其他材料相比,预测的准确性更高。本研究中的115个水稻亲本都是独立的纯系品种,而575个杂交种很多具有共同的父本或母本。在交叉验证时,杂交种训练集和测试集的亲缘关系较亲本之间更近,这明显有利于提高预测能力。本研究对杂交种进行预测时,均匀随机分组的预测效果最好,横向随机分组最差,很可能也是源于训练集和测试集之间变化的亲缘关系结构。
3.3 非加性效应的估计对SCA预测能力的影响
Riedelsheimer等[7]曾利用全基因组标记预测玉米7个性状的GCA。近期Velez-Torres等[29]也对玉米亲本多个性状的GCA进行了预测,精度从0.49到0.61。然而利用全基因组上的标记预测水稻杂交种SCA在国际上则未见报道。对于水稻SCA的预测,本研究中两种方法的预测能力都较低。一般认为SCA是由基因的显性和上位性等非加性作用所决定,而本研究所考查的NCII水稻杂交种主要由加性效应控制。高遗传率性状没有获得高的SCA预测能力,原因可能在于高遗传率性状的大部分遗传分量都由加性方差得到了解释,因此未必具有较高的非加性方差,从而影响到SCA的预测能力。
上位性是基于全基因组上变异位点和位点间的互作[30]。本研究使用全基因组上的高密度标记,其上位性分析所涉及的变量太多,将构成一个自变量数目远远超过观察样本数的超饱和模型,所以上位性并未纳入模型,这可能在一定程度上影响了SCA的预测效果。另外SCA还包括基因与环境的互作效应,因此容易受环境的影响而波动[31],这一点也未能在模型中加以反映。所以如何改进模型和算法,在增强大数据处理能力的同时,更准确地估计上位性,提高对杂交种SCA的预测能力,还有待更深入的研究,以促进GS方法更好地服务于水稻等作物的杂交育种工作。
[1] Meuwissen T H, Hayes B J, Goddard M E. Prediction of total genetic value using genome-wide dense marker maps., 2001, 157(4): 1819-1829.
[2] Lande R, Thompson R. Efficiency of marker-assisted selection in the improvement of quantitative traits., 1990, 124(3): 743-756.
[3] 王欣, 孙辉, 胡中立, 徐辰武. 基因组选择方法研究进展. 扬州大学学报: 农业与生命科学版, 2018, 39(1): 64-70.
Wang X, Sun H, Hu Z L, Xu C W. The research progress of genomic selection methods., 2018, 39(1): 64-70.
[4] Heslot N, Yang H-P, Sorrells M E, Jannink J-L. Genomic selection in plant breeding: A comparison of models., 2012, 52(1): 146-160.
[5] Lee Y-S, Kim H-J, Cho S, Kim H. The usage of an SNP-SNP relationship matrix for best linear unbiased prediction (BLUP) analysis using a community-based cohort study., 2014, 12(4): 254-260.
[6] Wang X, Xu Y, Hu Z, Xu C. Genomic selection methods for crop improvement: Current status and prospects., 2018, 6(4): 330-340.
[7] Riedelsheimer C, Czedik-Eysenberg A, Grieder C, Lisec J, Technow F, Sulpice R, Altmann T, Stitt M, Willmitzer L, Melchinger A E. Genomic and metabolic prediction of complex heterotic traits in hybrid maize., 2012, 44(2): 217-220.
[8] Crossa J, Perez-Rodriguez P, Cuevas J, Montesinos- Lopez O, Jarquin D, de los Campos G, Burgueno J, Gonzalez-Camacho J M, Perez-Elizalde S, Beyene Y, Dreisigacker S, Singh R, Zhang X C, Gowda M, Roorkiwal M, Rutkoski J, Varshney R K. Genomic selection in plant breeding: Methods, models, and perspectives., 2017, 22(11): 961-975.
[9] Guo T, Yang N, Tong H, Pan Q, Yang X, Tang J, Wang J, Li J, Yan J. Genetic basis of grain yield heterosis in an "immortalized F-2" maize population., 2014, 127(10): 2149-2158.
[10] Da Y, Wang C, Wang S, Hu G. Mixed model methods for genomic prediction and variance component estimation of additive and dominance effects using SNP markers., 2014, 9(1): e87666.
[11] Finley AO, Banerjee S, Waldmann P, Ericsson T. Hierarchical spatial modeling of additive and dominance genetic variance for large spatial trial datasets., 2009, 65(2): 441-451.
[12] Gianola D, de los Campos G, Hill W G, Manfredi E, Fernando R. Additive genetic variability and the Bayesian alphabet., 2009, 183(1): 347-363.
[13] Ibanez-Escriche N, Fernando RL, Toosi A, Dekkers J C M. Genomic selection of purebreds for crossbred performance., 2009, 41(1): 1-10.
[14] Wang X, Li L, Yang Z, Zheng X, Yu S, Xu C, Hu Z. Predicting rice hybrid performance using univariate and multivariate GBLUP models based on North Carolina mating design II., 2017, 118(3): 302-310.
[15] Wang X, Yang Z, Xu C. A comparison of genomic selection methods for breeding value prediction., 2015, 60(10): 925-935.
[16] Zhang Z, Erbe M, He J, Ober U, Gao N, Zhang H, Simianer H, Li J. Accuracy of whole-genome prediction using a genetic architecture-enhanced variance- covariance matrix., 2015, 5(4): 615-627.
[17] van Raden P M. Efficient methods to compute genomic predictions., 2008, 91(11): 4414-4423.
[18] Nishio M, Satoh M. Including dominance effects in the genomic BLUP method for genomic evaluation., 2014, 9(1): e85792.
[19] Forni S, Aguilar I, Misztal I. Different genomic relationship matrices for single-step analysis using phenotypic, pedigree and genomic information., 2011, 43(1): 43-53.
[20] Gilmour A R, Thompson R, Cullis B R. Average information REML: An efficient algorithm for variance parameter estimation in linear mixed models., 1995, 51(4): 1440-1450.
[21] Ashida I, Iwaisaki H. An expression for average information matrix for a mixed linear multi-component of variance model and REML iteration equations., 1999, 70(5): 282-289.
[22] Xu S, Zhu D, Zhang Q. Predicting hybrid performance in rice using genomic best linear unbiased prediction., 2014, 111(34): 12456-12461.
[23] Dan Z, Chen Y, Xu Y, Huang J, Huang J, Hu J, Yao G, Zhu Y, Huang W. A metabolome-based core hybridization strategy for the prediction of rice grain weight across environments., 2018, https://doi. org/10.1111/pbi.13024.
[24] Goddard M. Genomic selection: prediction of accuracy and maximisation of long term response., 2009, 136(2): 245-257.
[25] Goddard M E, Hayes B J. Mapping genes for complex traits in domestic animals and their use in breeding programmes., 2009, 10(6): 381-391.
[26] van Raden P, van Tassell C, Wiggans G, Sonstegard T, Schnabel R, Taylor J, Schenkel F. Invited review: Reliability of genomic predictions for North American Holstein bulls., 2009, 92(1): 16-24.
[27] Habier D, Tetens J, Seefried F-R, Lichtner P, Thaller G. The impact of genetic relationship information on genomic breeding values in German Holstein cattle., 2010, 42(1): 5.
[28] Riedelsheimer C, Endelman J B, Stange M, Sorrells M E, Jannink J L, Melchinger A E. Genomic predictability of interconnected biparental maize populations., 2013, 194(2): 493-503.
[29] Velez-Torres M, Garcia-Zavala J J, Hernandez-Rodriguez M, Lobato-Ortiz R, Lopez-Reynoso J J, Benitez- Riquelme I, Mejia-Contreras J A, Esquivel-Esquivel G, Molina-Galan J D, Perez-Rodriguez P, Zhang X C. Genomic prediction of the general combining ability of maize lines (L.) and the performance of their single crosses., 2018, 137(3): 379-387.
[30] Mao D, Liu T, Xu C, Li X, Xing Y. Epistasis and complementary gene action adequately account for the genetic bases of transgressive segregation of kilo-grain weight in rice., 2011, 180(2): 261-271.
[31] 钏兴宽. 配合力理论及其在水稻育种中的应用. 种子, 2014, 33(6): 39-41.
Chuan X K, Combining ability theory and its application in rice breeding., 2014, 33(6): 39-41.
Genomic Prediction of Combining Ability for Agronomic Traits in Rice Based on NCII Design
WANG Xin1,2,3, MA Ying1, HU Zhongli3, XU Chenwu1,*
(Jiangsu Key Laboratory of Crop Genetics and Physiology / Key Laboratory of Plant Functional Genomics of the Ministry of Education / Jiangsu Key Laboratory of Crop Genomics and Molecular Breeding, Agricultural College of Yangzhou University, Yangzhou 225009, China; College of Information Engineering, Yangzhou University, Yangzhou 225127, China; State Key Laboratory of Hybrid Rice, College of Life Sciences, Wuhan University, Wuhan 430072, China; )
【】It plays a key role in hybrid rice breeding to select hybrids with high specific combining ability based on high general combining ability of parental inbred lines. Genomic selection that is based on molecular markers across the whole genome and phenotypes of samples enable us to establish prediction models and achieve more reliable selection of varieties. 【】We investigated the genomic predictive ability of combining ability for agronomic traits in rice based on NCII design. And the effects of different training population construction methods on predictive ability of hybrid performance were compared. 【】The predictive abilities of general combining ability for eight agronomic traits, ranged from 0.3888 to 0.7367, were dominated by their heritability. The predictive ability of specific combining ability for hybrids was lower, but the ability of directly predicting phenotypes for hybrids was higher. 【】The genomic prediction of combining ability for rice parental lines is effective and can help breeders to select parents effectively. With regard to hybrid selection, direct predicting phenotypes of hybrids is the most effective method. At this time, allowing more parents to participate in the crosses for hybrid training set in a balanced way is benefical to obtain higher predictive ability.
rice; incomplete diallel cross; phenotype; combining ability; genomic prediction
S511.032
A
1001-7216(2019)04-0331-07
10.16819/j.1001-7216.2019.9025
2019-02-28;
2019-04-23。
国家863计划资助项目(2014AA10A601-5);杂交水稻国家重点实验室(武汉大学)开放课题基金资助项目(KF201701)。

