基于改进局部保持投影的转盘轴承退化指标研究

戴永奋，包伟刚，王华

(1.马鞍山方圆精密机械有限公司，安徽 马鞍山 243041; 2.南京工业大学 机械与动力工程学院，南京 211816)

转盘轴承是一种尺寸较大的转动部件，广泛应用于大型风力发电机、塔式起重机以及盾构机等机械主机中。转盘轴承工作于低速、重载的工况，其平稳运行往往关系到机械设备的可靠性，因此对其进行合理的健康评估具有重要意义。

1 研究背景

目前，数据驱动方法广泛应用于各类旋转部件中，对基于人工智能的数据驱动评估策略[1]而言，寻找一种合适的退化指标用以描述研究对象的退化趋势在一定程度上决定着寿命模型的准确性。转盘轴承作为一种特殊功能部件，其损伤、退化机理尚未完全明朗，如何通过数据驱动的模型研究其运行稳定性及寿命情况成为近年国内外的研究热点。文献[2]提取了转盘轴承全周期振动信号的时域指标，通过主成分分析法(PCA)提取退化指标输入最小二乘向量机模型，得到了较好的评估结果；文献[3]将概率主成分分析(PPCA)应用于转盘轴承的状态识别并获得优于传统PCA方法的分类效果；文献[4]同样通过PCA降维，利用温度和扭矩特征提取转盘轴承退化指标描述其健康情况；文献[5]采用了圆域指标对转盘轴承进行故障诊断，并指出该类指标不具备连续描述退化趋势的能力；文献[6]对转盘轴承振动以及声信号进行研究并借助集合经验模态分解和PCA相结合的方法进行多尺度故障诊断，比传统PCA故障诊断可靠性更高。

综上所述，目前的研究大多采用特征融合的方法提取全寿命阶段退化指标[7]，虽兼顾了各种特征的差异性，但往往忽视了融合算法自身特性对于评估精度的影响。且受转盘轴承复杂受力特性以及恶劣工况等因素的影响，使得这种全局线性融合算法在一定程度上未能完全表征复杂的退化过程。如何充分挖掘状态监测数据的有用信息，剔除冗余成分且更加贴切描述转盘轴承的复杂退化过程值得深入研究。

局部保持投影(Local Preserving Projection，LPP)是一种兼顾局部特征的数据融合方法[8]，在轴承健康监测、故障诊断领域得到了广泛应用：文献[9]提出一种局部及非局部保持投影(Local and Nonlocal Preserving Projection，LNPP)，旨在保证相同簇内结构的同时最大化不同簇间的距离；文献[10]通过Parzen窗概率密度估方法自适应地确定LPP算法中的邻域参数；文献[11]采用正交局部保持投影方法(Orthogonal Locality Preserving Projection, OLPP)对轴承进行故障程度的描述。

现有研究主要集中在如何确定LPP参数及邻域空间，而机械系统各组成部件间的耦合等现象使得不同退化特征相互联系，但以欧式距离为基础构建邻域空间的LPP方法无法兼顾这种潜在的关联性。因此，对传统LPP算法进行度量空间的改进，引入马氏距离(Mahalanobis Distance，MD)代替欧式距离，以减弱不同邻域特征的值域区间对于特征融合的影响，同时兼顾不同退化特征的潜在关系。

2 改进的局部保持投影及转盘轴承健康评估流程

作为一种流形学习算法，LPP在滚动轴承故障诊断领域被广泛使用，但在转盘轴承中的应用鲜有报导。此外，转盘轴承损伤机理复杂，国内外学者普遍采用多物理信号监测其运行情况[4, 12]，不同物理信号的区间有很大差异。欧式空间一定程度上受退化特征值域影响较大且在具有强烈相关的指标间表现不理想，因此采用马氏距离代替欧式距离构造近邻空间。

2.1 马氏距离

马氏距离[13]这种度量尺度不受输入向量的区间范围影响，并能很好地减弱不同特征指标间的强相关性，其具体公式可表示为

(1)

式中：X={Xi|i=1,…,n}，Y={Yi|i=1,…,n}分别为2种退化特征向量；C为2组向量的协方差矩阵。

2.2 基于马氏距离的局部保持投影

流形学习旨在发现高维空间中的低维流形结构，LPP在此基础上充分保留了各高维特征间的局部关系。其主要步骤如图1所示。

图1 LPP的基本流程

在传统LPP算法的基础上，对构造近邻分布进行了基于马氏距离的改造，具体流程如下：

1)计算样本点Xi的协方差矩阵C，并得到马氏距离DM；

2)选择并更新Xi的近邻点，构造近邻分布[8]；

3)直至遍历所有Xi；

4)得到近邻分布。

2.3 转盘轴承健康评估流程

基于改进后LPP特征融合方法的转盘轴承健康评估要包括以下6块：1)原始信号采集；2)降噪处理；3)各邻域特征提取(具体各邻域特征向量表达式见表1)；4)特征筛选；5)基于马氏距离的LPP特征融合；6)基于数据驱动方法的健康评估。具体流程如图2所示。

原始信号采用振动、温度、扭矩的多物理信号输入，保证能够全面描述转盘轴承的退化趋势；此外，在高维特征融合前加入了轨迹差异性筛选过程，通过计算不同特征指标间的相似度剔除高相似度特征，增加退化特征的差异性。轨迹差异性计算公式为

(2)

计算每种信号下各特征间的差异性值，该值越大则说明两者间存在越大的轨迹差异性。提取存在较大差异性的指标，从而减轻后续健康评估模型的过拟合效应。

表1 多邻域特征

图2 转盘轴承健康度评估流程

3 全寿命加速试验

结合QNA-730-22型转盘轴承(具体参数见表2)全寿命加速疲劳寿命试验验证基于马氏距离的LPP退化指标，并通过与PCA，LPP的对比进一步确认基于马氏距离的LPP退化指标对于健康评估模型的有效性。

表2 转盘轴承主要参数

3.1 试验介绍

试验由自主研发的转盘轴承试验台完成，如图3所示，试验台主要由机械主体，液压加载系统和测控系统3部分组成，其中液压系统通过3个不同液压缸的组合模拟各种工况。

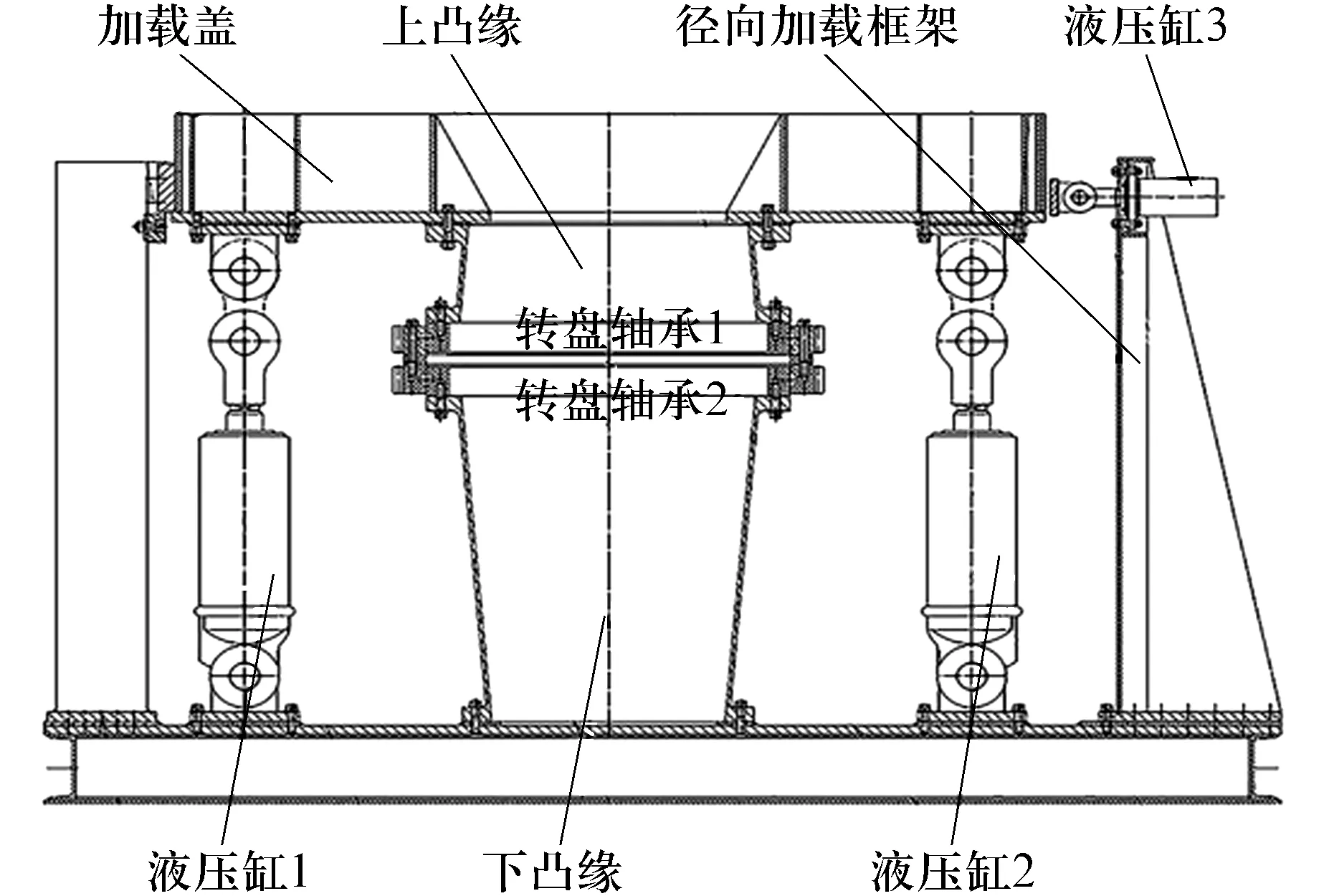
图3 转盘轴承试验台

本次全寿命加速疲劳试验共持续12 d左右，试验原始数据如图4所示，试验前以及动圈完全卡死后轴承的拆机结果如图5所示。从图中可以看出，球、内圈以及保持架均存在明显损伤，已无法正常服役，所选的3种信号具有一定的变化趋势，但不直观，仍需进一步处理。

图4 试验原始数据

图5 试验前、后转盘轴承的拆解示意图

3.2 数据分析

通过轨迹差异性计算筛选优胜退化特征，具体计算结果见表3—表5，表中所列特征间的轨迹差异性值均为归一化后的计算结果，这样可以避免不同退化特征由于值域差异对最终剔除结果的影响。由表可知：振动退化特征中绝对平均幅值Xra以及均方根Xrms与其他特征差异性较小；温度退化特征中最大值Xmax与其他特征差异性较小；扭矩退化特征中方差Xv与其他特征差异性较小，故剔除Xra，Xrms，Xmax，Xv这4个指标。

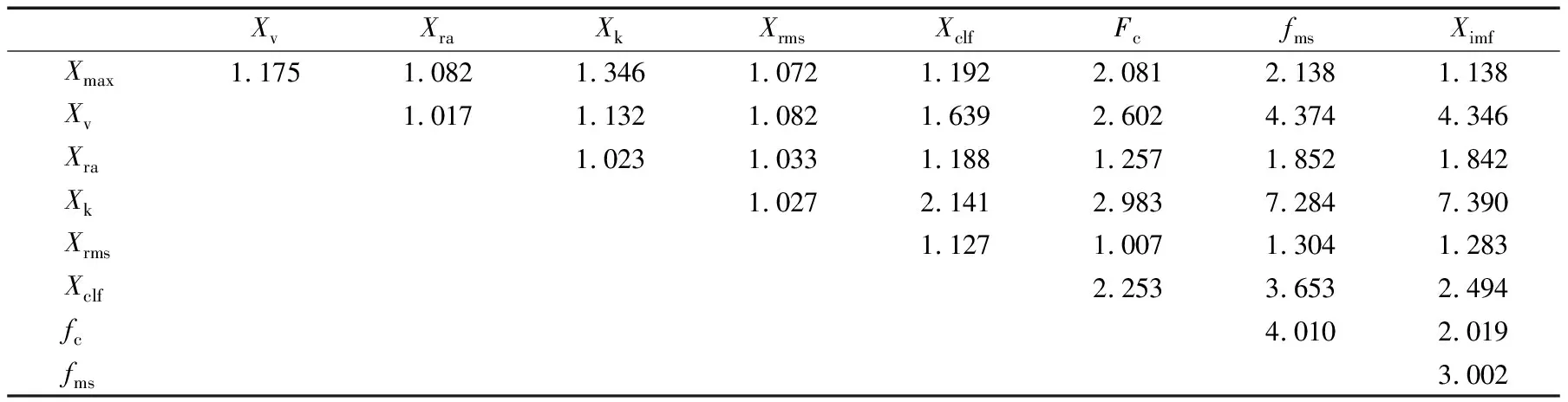
表3 振动退化特征筛选

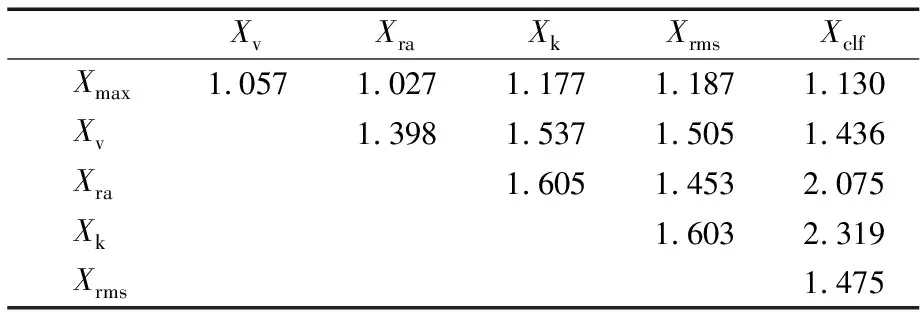
表4 温度退化特征筛选

表5 扭矩退化特征筛选

随后，采用较为常用的PCA，LPP，LNPP，OLPP与基于马氏距离的LPP对筛选后的特征进行融合降维处理，生成退化指标。为保证各算法处于同一水平，特征融合之前的评估流程(图2)均相同。此外，由于LPP中的参数选择是影响最终退化轨迹的重要因素，而近邻点K以及热核函数中的参数α尚未有很好的确定方法。文献[14]初步确定近邻点数的选择区间，但未准确给出二者的确定取值；在其基础上，设计了一种以最大化单调性指标为目标函数的寻优方法，即

(3)

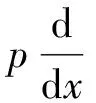
5种算法对退化指标的描述如图6所示，从图中可以看出：PCA及OLPP的振动退化指标在600点左右时单调性发生改变，与机械部件损伤退化趋势的不可逆性相悖；此外，PCA，LNPP的扭矩退化指标，基于欧式距离的LPP的振动退化指标抖动明显，噪声显著，可能会加剧数据驱动模型的过拟合效应；基于马氏距离的LPP退化指标在3种信号下无明显抖动并且轨迹平滑，其单调性在全寿命周期内没有显著、频繁地变化，能够较好地反应转盘轴承的退化情况。

为进一步验证改进的LPP退化指标的有效性，采用4种不同评估模型分别对5种指标进行剩余寿命预测，评价指标为均方根误差 (RMSE)和平均绝对误差 (MAE)。随机取1/3样本点作为训练集，剩余点为验证集，输入为振动、温度以及扭矩退化指标，输出为剩余寿命，不同数据驱动模型下5种指标的健康评估情况见表6。由表可知：欧式距离下退化指标所建立的模型预测误差均大于马氏距离；基于马氏距离的LPP退化指标在4种不同健康评估模型中预测误差最小； LSSVM模型具有较优的剩余寿命预测能力，BP神经网络(BPNN)预测能力较弱且受网络结构以及参数影响较大。

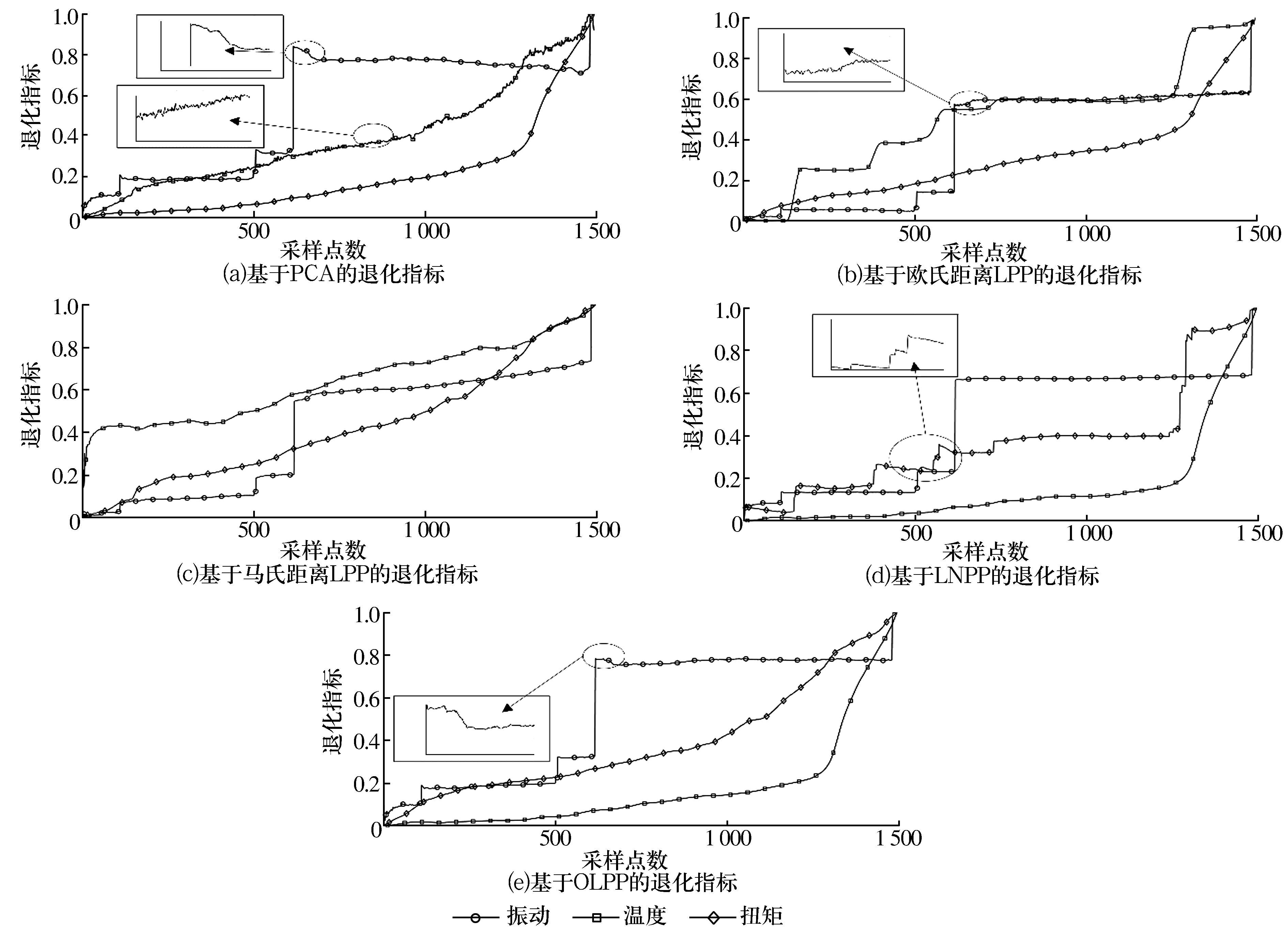
图6 不同算法的退化指标

表6 退化指标间的健康评估性能比较

4 结束语

提出了基于马氏距离的改进LPP转盘轴承退化指标描述，通过试验得到如下结论：1)基于马氏距离的LPP退化指标具备较好的剩余寿命预测能力，能够较为准确地反应退化过程；2)局部保持投影算法注重挖掘高维特征中的低维局部流形结构，这一点比致力于保持全局结构的PCA融合算法更加符合转盘轴承的复杂退化特性。该方法从几何邻域关系描述出发,改进传统欧式距离的流形学习算法，与现有方法相比具有一定优越性，同时,基于马氏距离的LPP算法可以与其他改进方法相结合，深入探索流形学习方法在机械部件健康评估中的具体影响因素。