沟道表面波纹度对高速球轴承保持架打滑的影响

张东光，牛蔺楷

(太原理工大学 机械与运载工程学院，太原 030024)

高速球轴承广泛应用于航空、航天、能源、高档数控机床等关键领域。高速工况下轴承振动会对整个设备的安全性和可靠性产生严重的影响。表面波纹度、局部损伤、保持架碰撞等均会影响轴承的振动特性[1-5]。

表面波纹度是轴承表面的主要形状误差之一[6]。文献[1]通过建立多体动力学模型分析了表面波纹度对球轴承动力学特性的影响。文献[7]分析了表面波纹度的阶数和最大幅值对轴承-转子系统振动的影响。文献[8]基于弹性流体动力润滑理论建立了球与沟道之间的润滑模型，分析了在润滑良好及润滑苛刻2种条件下表面波纹度对轴承振动特性的作用。文献[9]建立了双列圆锥滚子轴承的动力学分析模型，并基于此模型分析了波纹度对轴承振动的影响。

高速球轴承的另一个主要振源是保持架动态特性。文献[10-12]构建了目前最具代表性的高速球轴承动力学分析模型。GUPTA模型考虑了轴承中球、套圈及保持架在高速运行下的三维运动、相对滑动、润滑牵引等复杂动力学问题以及离心、陀螺等高速效应，并通过试验进行了验证[12]。文献[13]基于GUPTA模型分析了球轴承保持架的热稳定性问题。文献[14]通过引入黏滞阻尼系数对GUPTA模型进行了改进，分析了球轴承几何和工况参数对保持架打滑的影响。文献[15]基于GUPTA模型分析了保持架载荷(保持架兜孔与球之间的接触力与摩擦力，保持架与引导套圈之间的接触力与摩擦力，保持架离心力)在保持架稳态运动中所起的作用。文献[16]通过建立非线性动力学微分方程分析了滚动轴承的保持架打滑问题。文献[17]分析了加速过程中滚动轴承保持架的打滑问题。

上述对表面波纹度和保持架动态特性做了大量研究，但研究尚不深入。表面波纹度会影响球与沟道之间的几何趋近量并严重影响接触载荷，接触载荷又会进一步影响球的运动特性，并对球与保持架之间的碰撞作用产生影响，最终影响保持架打滑特性。较大的保持架打滑会加剧保持架磨损，导致保持架产生裂纹。鉴于此，在GUPTA球轴承模型的基础上分析轴承套圈表面波纹度对保持架打滑特性的影响。

1 考虑沟道表面波纹度的高速球轴承动力学模型

GUPTA模型未考虑套圈表面波纹度，在GUPTA模型中引入表面波纹度,建立考虑轴承表面波纹度的高速球轴承动力学模型。

1.1 动力学建模

外圈与球相互作用如图1所示，图中：Oixiyizi为惯性坐标系，Oe为外圈中心，Ob为球中心，C为外沟道曲率中心。以球中心为中心建立球坐标系Obxbybzb，以外圈中心为中心建立外圈坐标系Oexeyeze。

球中心相对于外圈中心的位置矢量为

rbr=rb-rr，

(1)

式中：rb为球中心的位置矢量;rr为外圈中心的位置矢量。

外沟道曲率中心相对球中心的位置矢量为

rbc=rbr-rcr，

(2)

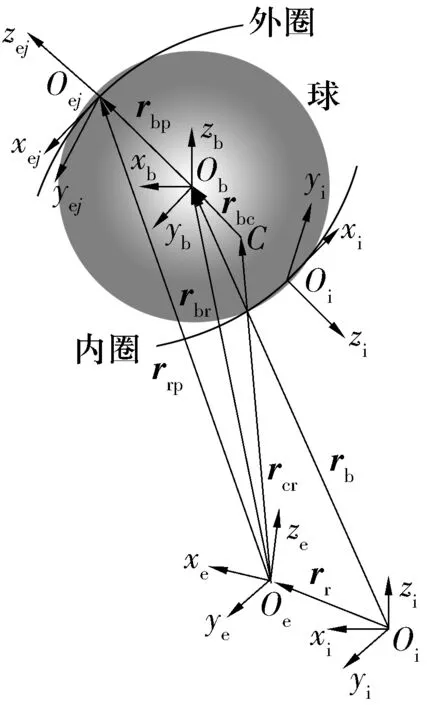
图1 外圈与球相互作用

式中：rcr为外沟道曲率中心相对外圈中心的位置矢量。

外圈沟道与球之间的几何趋近量为

δe=rbc3-(fe-0.5)Dw，

(3)

式中：rbc3为矢量rbc在接触法线方向的分量；fe为外沟曲率半径系数；Dw为球直径。

根据Hertz接触理论可得外圈与球之间的接触载荷为

(4)

式中：k为Hertz接触刚度系数。

求得外圈与球之间的接触载荷后，根据2个轴承零件的速度矢量可得到二者之间在接触区的相对滑动速度。为计算球与外圈的相对滑动速度，建立第j个球与外圈接触坐标系Oejxejyejzej，该坐标系的zej轴垂直于接触面，yej轴沿球旋转方向，xej轴通过右手螺旋法则确定。假设外圈和球的平移速度矢量分别为vr和vb，旋转速度矢量分别为ωr和ωb，则两者相对滑动速度矢量为

u=vr+ωr×rrp-vb-ωb×rbp，

(5)

式中：rrp和rbp分别为接触点相对于外圈中心和球中心的位置矢量(图1)。

将相对滑动速度矢量u在xej，yej轴的分量代入一定的润滑牵引模型即可得到相对应的牵引系数(摩擦因数)。典型润滑牵引模型为[18]

(6)

式中：μ为牵引系数；A为常数；v为滑动速度；v0为临界滑动速度。

将xej，yej方向的牵引系数与法向接触载荷相乘可得到牵引力Fsex和Fsey(图2)。法向接触载荷和牵引力共同构成了外圈作用于球的载荷矢量，即

(7)

则球作用于外圈的载荷矢量为

Feb=-Fbe，

(8)

通过将载荷矢量与相应的位置矢量做叉积运算即可得到外圈作用于球的力矩矢量

Μbe=rbp×Fbe，

(9)

球作用于外圈的力矩矢量为

Μeb=rrp×Feb。

(10)

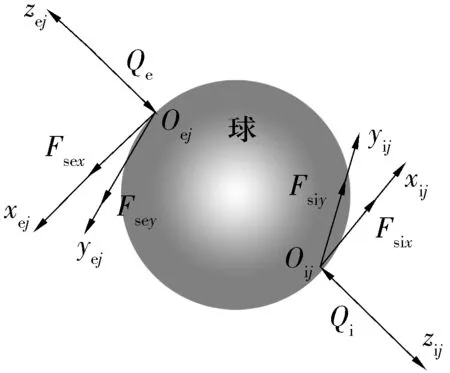
图2 套圈作用在球上的载荷

内圈作用于球的力如图2所示。图中：Qi为球与内圈的接触载荷；Oijxijyijzij为球与内圈接触坐标系(zij轴垂直于接触面，yij轴沿球的旋转方向，xij轴通过右手螺旋法则确定)。内圈与球的相互作用力及力矩同外圈计算方法。

球与保持架之间的相互作用如图3所示。图中：Oc为保持架中心；Op为保持架兜孔中心。

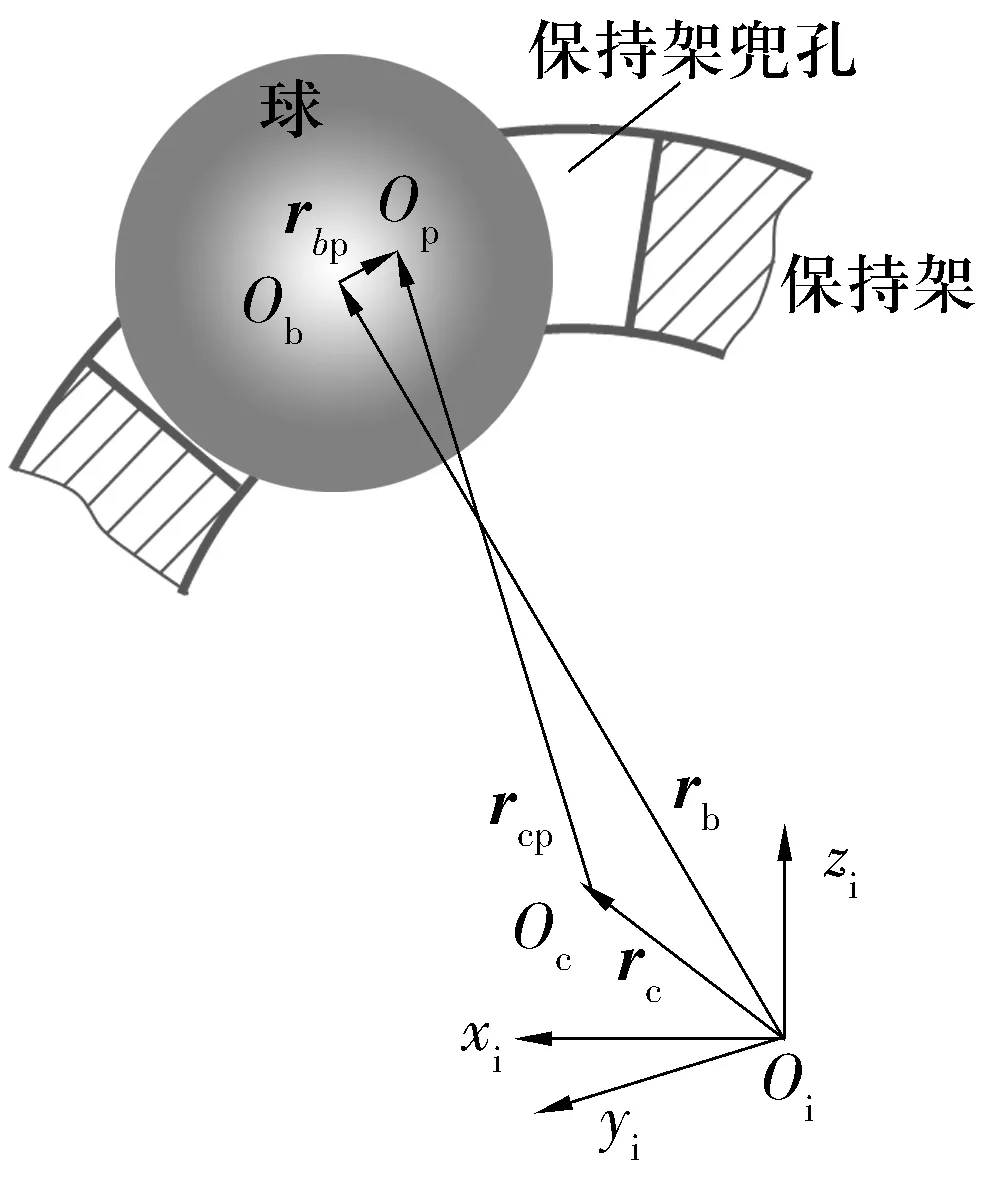
图3 球与保持架相互作用

保持架兜孔中心相对球中心的位置矢量为

rbp=rb-rc-rcp，

(11)

式中：rcp为保持架兜孔中心相对保持架中心的位置矢量。

球与保持架兜孔之间的几何趋近量为

h=Cp-rbp2，

(12)

式中：Cp为保持架兜孔间隙；rbp2为矢量rbp在球与保持架兜孔壁接触法线方向的分量。

同球与外圈之间相互作用关系类似，得到球与保持架兜孔之间的几何趋近量，可计算二者之间的接触载荷，并在此基础上计算力及力矩。

在得到球、内圈、外圈以及保持架的力和力矩后，采用牛顿第二定律描述各轴承零件的平移运动，即

(13)

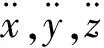
采用EULER方程描述各轴承零件的转动，即

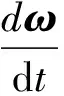
(14)

式中：J为惯性主矩矢量；ω为角速度矢量；M为力矩矢量。

GUPTA模型中未考虑轴承座的影响，在GUPTA模型的基础上额外增加2个自由度以模拟轴承座的动力学特性，如图4所示(Oxyz为以轴承中心为原点建立的坐标系)。轴承所承受的径向载荷Fr沿z轴负方向。另外，轴承所承受的轴向力Fa沿x轴方向，该轴向力未在图4中标出。轴承座动力学方程为[2]

(15)

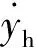
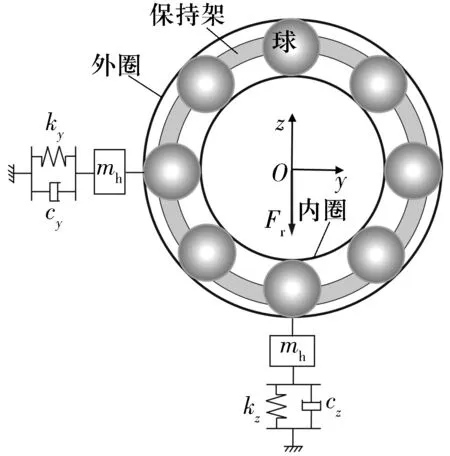
图4 轴承座模型

1.2 表面波纹度建模

沟道表面波纹度模型如图5所示，采用余弦函数序列对套圈表面波纹度进行建模。内、外圈表面波纹度可表示为[7]

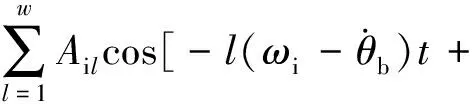
2πl(j-1)/Z+αil]，

(16)

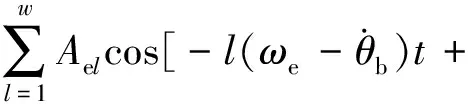
2πl(j-1)/Z+αel]，

(17)

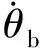
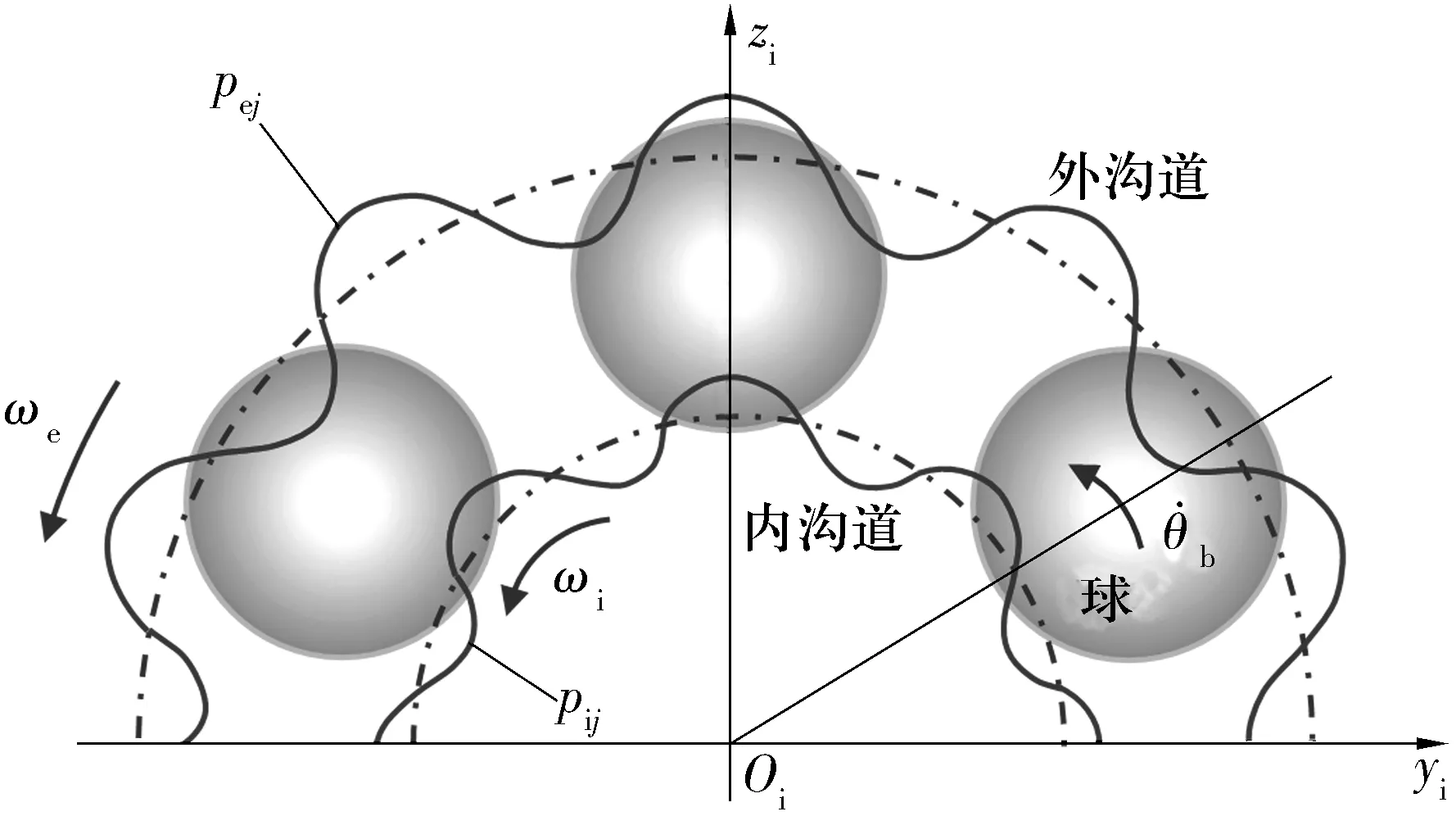
图5 沟道表面波纹度模型

通过GUPTA模型计算可得内、外圈与球之间的趋近量分别为δi和δe。考虑表面波纹度的影响，将(3)式计算得到的几何趋近量δi和δe分别改为(δi+pij)和(δe+pej)。

2 仿真分析

对轴承进行动力学特性分析，需要对(13)～(15)式进行动力学积分。在此采用4/5阶变步长Runge-Kutta法对动力学方程进行数值求解。为加快动力学积分的收敛速度，首先采用拟静力学模型[18]获得积分初值(包括各轴承零件的初始位置、初始平移速度和初始角速度)。轴承系统的主要参数见表1。球与沟道之间的牵引系数与相对滑动速度之间的关系为[19]

(18)

仿真计算流程如图6所示。

保持架在高速、轻载工况下易出现严重打滑，并引起轴承失效,保持架打滑率Δωc为

(19)

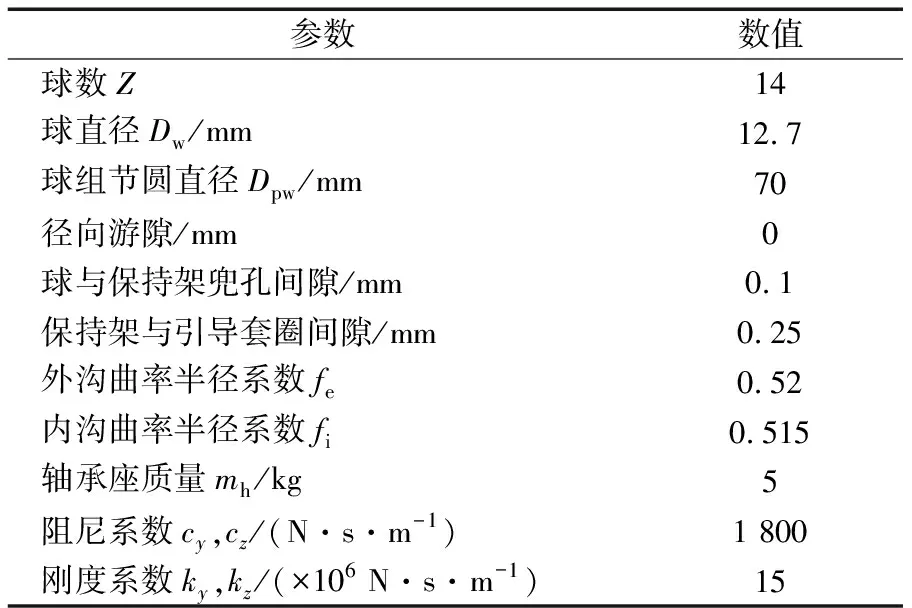
表1 轴承系统的主要参数

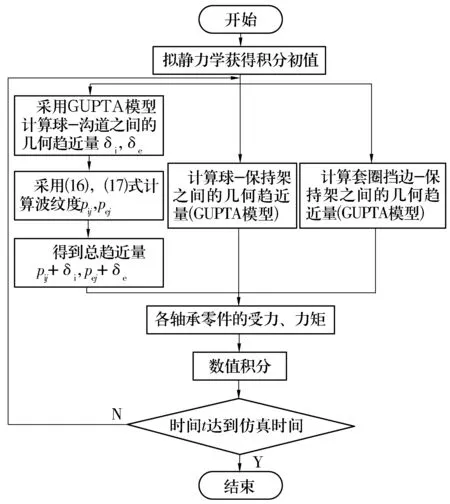
图6 仿真计算流程

式中：ωc为采用动力学模型计算得到的保持架转速。按照(14)式对时间进行积分后得到保持架的角速度矢量，ωc即保持架角速度矢量沿x轴方向的分量。

2.1 波纹度最大幅值对打滑率的影响

在轴向力为100 N，径向力为1 000 N，转速为10 000 r/min，波纹度波数为14时套圈波纹度最大幅值A对保持架打滑率的影响如图7所示。由图7a可以看出：随内圈波纹度最大幅值增大，保持架打滑率平均值也随之减小(当内圈波纹度最大幅值分别为0.1，0.5和2.0 μm时，保持架打滑率平均值分别为5.194，4.655和2.368);由图7b可以看出：随外圈波纹度最大幅值增大，保持架打滑率平均值降低(当外圈波纹度最大幅值分别为0.1，0.5和2.0 μm时，保持架打滑率平均值分别为5.216，4.092和2.094):表明保持架打滑率随着波纹度最大幅值的增大而减小。这可能是由于较大的波纹度最大幅值改变了球与沟道之间的接触载荷及切向牵引力，从而进一步影响了球与保持架兜孔之间的相互作用力，使球在保持架运行的过程中能够不停地推动保持架进行转动，从而减小了保持架打滑率。但是由图7还可看出：当波纹度最大幅值增大后，Δωc的波动增大。这说明波纹度最大幅值增大会使保持架转速的波动变大，保持架运转的稳定性变差。

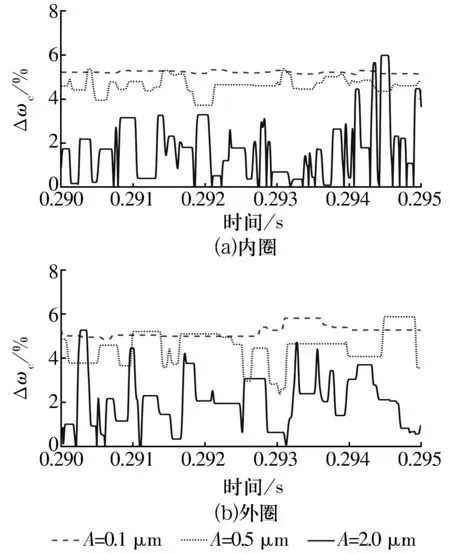
图7 表面波纹度最大幅值对打滑率的影响

2.2 波纹度波数对打滑率的影响

在轴向力为100 N，径向力为1 000 N，转速为10 000 r/min，波纹度最大幅值为0.1 μm时波纹度波数w对打滑率的影响如图8所示。通过统计学指标峰值系数(即峰值与均方根值的比值)分析波纹度波数对保持架打滑率的影响。在图8a中，当波纹度波数分别为7，10，14和17时，所对应的保持架打滑率的峰值系数分别为1.003，1.003，1.055和1.156,说明随内圈波纹度波数增大，保持架打滑率峰值系数增大;在图8b中，当波纹度波数分别为7，10，14和17时，所对应的保持架打滑率峰值系数分别为1.026，1.027，1.025和1.027,说明外圈波纹度波数增大，保持架打滑率峰值系数无明显变化。这可能是由于内圈波纹度波数对球与沟道之间的接触载荷和切向牵引力的影响更大，从而影响球与保持架兜孔之间的相互作用力。从上述分析可以看出：保持架打滑率有随内圈波纹度波数的减小而减小的趋势。

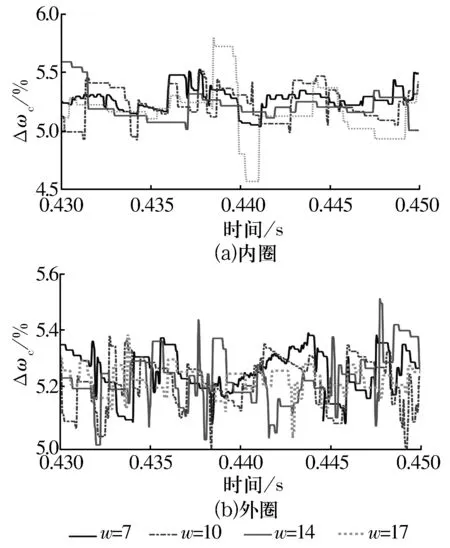
图8 表面波纹度波数对打滑率的影响

2.3 不同轴向力下保持架打滑特性

轴承承受纯轴向力作用，在轴承转速为10 000 r/min，波纹度最大幅值为0.1 μm，波纹度波数为14时轴向力对保持架打滑率的影响如图9所示。由图9可以看出：轴向力越大，保持架打滑率越小。为减小打滑率，可增大轴向力;但较大的轴向力会产生摩擦热，影响轴承寿命[20]。轴向力的选择需要进一步优化分析。

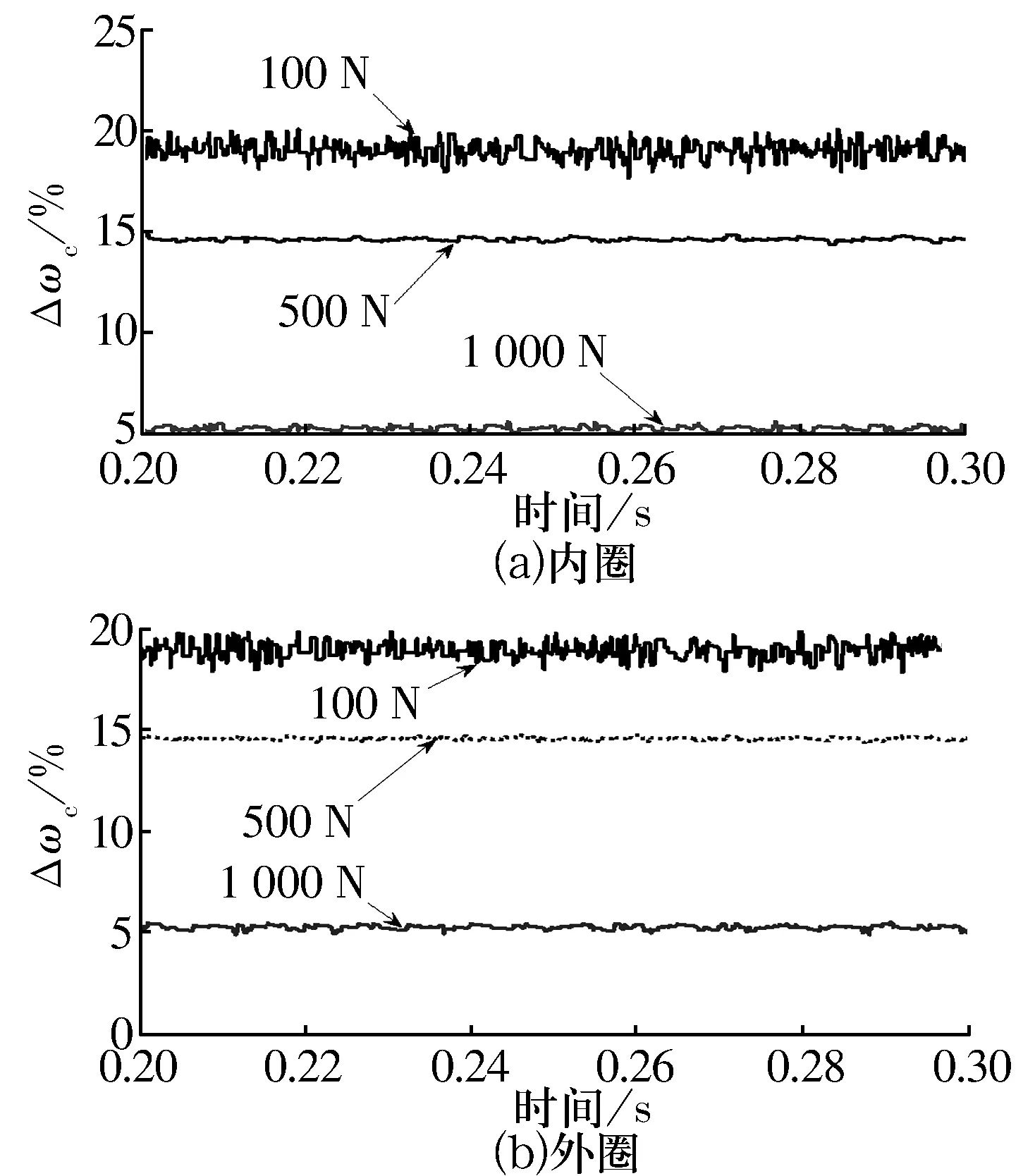
图9 轴向力对保持架打滑率的影响

在纯轴向力1 000 N时，内圈表面波纹度对保持架打滑率的影响如图10所示。由图10可以看出：1)内圈表面波纹度波数越大，打滑率变动范围越大;2)内圈表面波纹度最大幅值越大，保持架打滑率在整个时间区间上平均值越小;减小内圈表面波纹度的阶数,增大内圈波纹度的最大幅值有利于减小保持架打滑率。

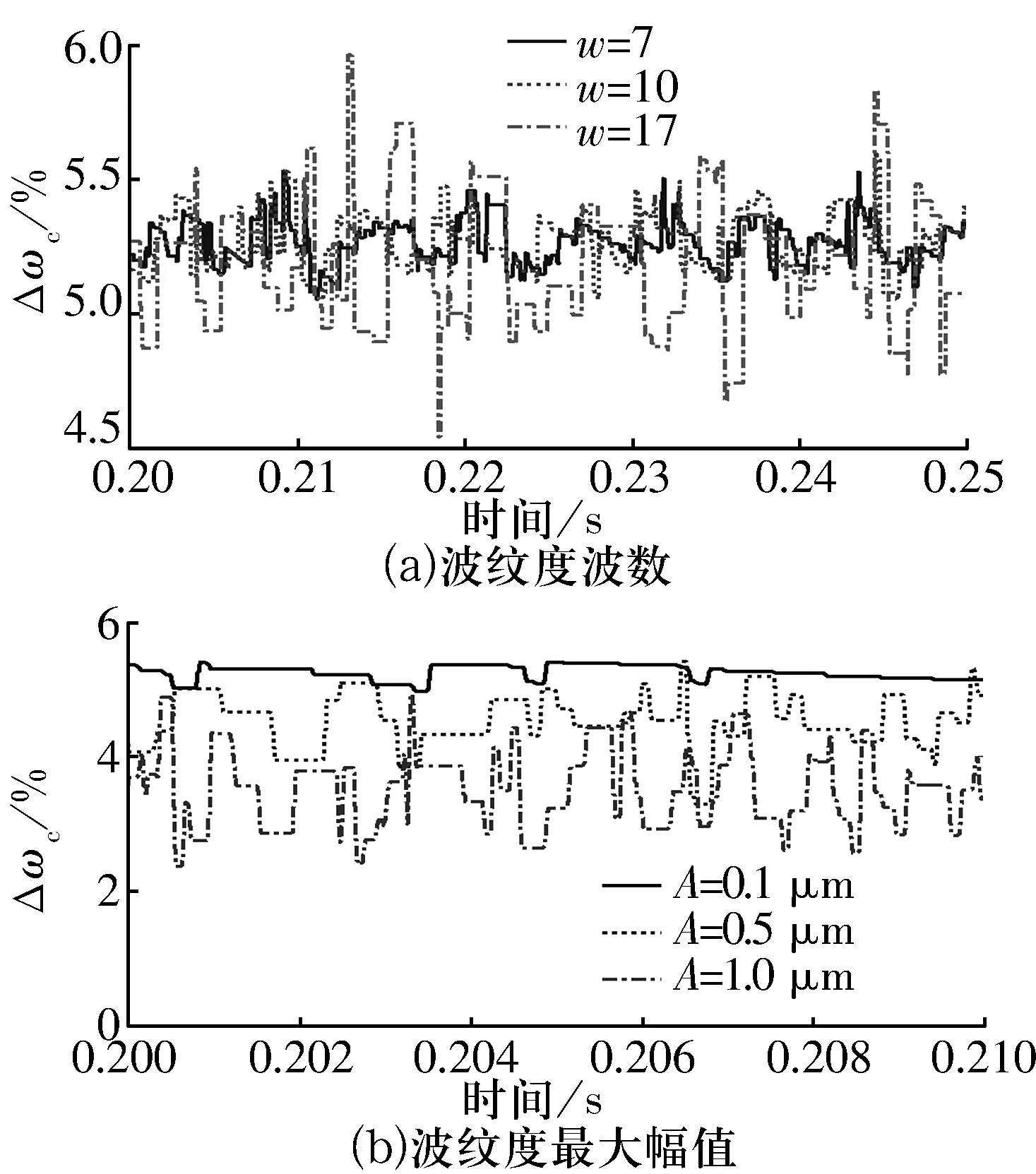
图10 轴向力为1 000 N时内圈波纹度对保持架打滑率的影响

在轴向力为1 000 N时外圈表面波纹度对保持架打滑率的影响如图11所示。由图11可以看出：1)外圈表面波纹度波数对打滑率影响不大;2)外圈表面波纹度最大幅值越大，保持架打滑率在整个时间区间上的平均值越小;3)增大外圈表面波纹度最大幅值有利于减小保持架打滑率。

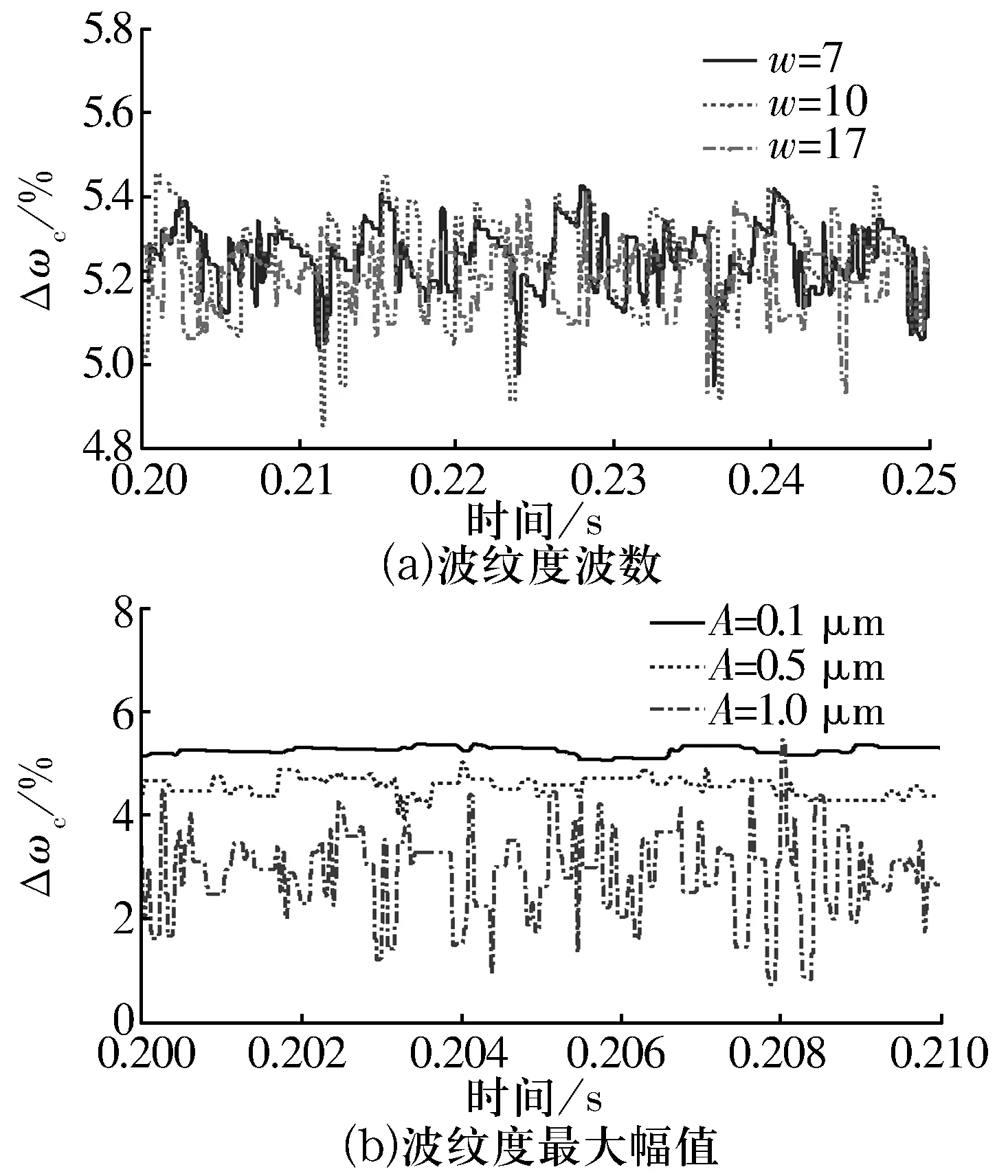
图11 轴向力为1 000 N时外圈表面波纹度对保持架打滑率的影响

3 模型验证

从频域角度分析表面波纹度对轴承的振动响应，并将仿真分析结果与文献[9]研究结果进行对比，以验证所建立动力学模型的正确性和有效性。

轴承的结构与工况参数与第2.1和2.2节的相同。在内、外圈表面存在波纹度时轴承基座振动频谱分别如图12和图13所示。

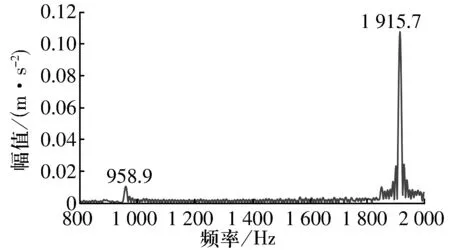
图12 外圈波纹度最大幅值为0.1 μm，波纹度波数为7时轴承基座振动频谱

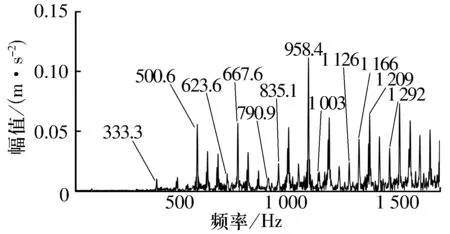
图13 内圈波纹度最大幅值为0.1 μm，波纹度波数为7时轴承基座振动频谱

由图12可以看出：在外圈表面存在波纹度情况下，在基座振动的频谱中找到球、外圈通过频率958.9 Hz及其倍频1 915.7 Hz，与文献[9]一致。

由图13可以看出,在内圈含有表面波纹度时，频谱中的频率成分可以分为2类：1)轴承转频fi的倍频，例如333.3 Hz(≈2fi)，500.6 Hz(≈3fi)，667.6 Hz(≈4fi)，835.1 Hz(≈5fi)，1 003 Hz(≈6fi)，1 166 Hz(≈7fi);2)近似等于pZfc±qfi(p和q为正整数，fc为保持架旋转频率)，例如623.6 Hz(≈14fc-2fi)，790.9 Hz(≈14fc-fi)，1 126 Hz(≈14fc+fi)，1 292 Hz(≈14fc+2fi)。这些频率的分布规律与文献[9]中相同。

综上可知，文中模型的分析结果与已有研究结果基本符合，验证了模型的有效性。

4 结论

基于GUPTA模型建立了考虑保持架效应以及沟道表面波纹度的动力学分析模型，分析了沟道表面波纹度对高速球轴承保持架打滑率的影响,得出结论：

1)保持架打滑率随表面波纹度幅值的增大而减小，但较大的波纹度幅值会使保持架的运行更不稳定。

2)保持架打滑率随内圈波纹度波数减小而减小。

3)适当增大轴向载荷有利于减小保持架打滑率。