基于可变模糊集的流域水资源配置评价研究

周如瑞，黄 青

（浙江省水利水电技术咨询中心，浙江 杭州 310020）

1 问题的提出

我国经济持续增长，人口不断增加，有限的水资源与人民生活水平快速提高、社会发展之间的矛盾十分突出。由于发电、供水、航运、环境保护之间存在着一定的协同性、关联性、竞争性，为满足水资源调控的多目标、多维度需求，通过水资源合理配置提高水资源利用率，可实现水资源的可持续利用。可持续发展水资源合理配置的核心是通过工程及非工程手段，对水资源在时间分布、空间分布、总量分配、分质供水和分行业供水上进行科学规划，满足水资源供给量与社会、经济、生态对水资源的需求量处于平衡状态，使配置后获得最大化的综合效益，达到可持续利用的目标[1]。然而，水资源配置结果是否科学、合理，对社会、经济、生态等目标是否达到预期，是否满足可持续利用的目标，需对配置模型结果的多个方案进行评价。社会、经济、生态目标均具有模糊性的特点，对其进行综合评价是个多目标的模糊概念，主要判别综合目标是否符合区域实际情况、能否促进水资源的可持续利用与社会经济的可持续发展。

国内很早就开始水资源配置评价的相关研究，并形成多项研究论文与专利，评价方法多样。从1970年开始陆续提出灰色系统理论、创立物元分析新学科，运用层次分析法、灰色关联度分析法、人工神经网络、投影寻踪决策法等评价方法[2]。实际上，流域水资源配置合理与否是一个模糊概念，而评价水资源配置的各个指标是确定的清晰值，如何采用模糊理论，并明确量化方法，评价水资源配置方案也是一个值得研究和应用的内容。

本文应用陈守煜在2005年创立的可变模糊集方法[3-7]，用清晰值去计算模糊概念水资源配置优劣的相对隶属度。以可变模糊集为理论基础，提出水资源配置多指标识别方法，详细论述该方法的基本思路和应用步骤，并通过引用已有文献中的计算方法和结果，对比说明该方法的有效性、合理性。

2 基于可变模糊集的水资源配置评价

如果一个系统有n个决策，并且每个决策有m个评价其优劣的目标特征值，则目标特征值矩阵可写为:

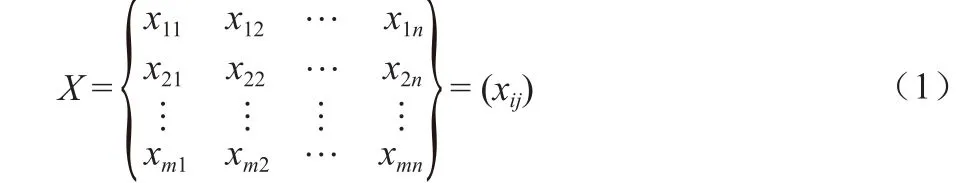
式中:xij为决策j的目标特征值；i = 1，2，…，n。

由于m个目标特征值的物理量纲不同，为了消除这种影响，需要将矩阵X规格化，即要将目标特征值xij变换为关于模糊概念的相对隶属度rij。通常有2类指标:

（1）越大越优效益型指标，即目标的特征值越大，聚类类别越靠前，其规格化公式:

（2）越小越优成本型指标，即目标的特征值越小，聚类类别越靠前，其规格化公式:

所以，指标特征值矩阵可以转换为各个指标对模糊概念A的相对隶属度矩阵，指标特征值规格化矩阵公式:

式中:rij为决策目标对优的相对隶属度，简称目标相对优属度。

由于m个目标具有不同的权重，设权向量为w:

对于权向量的确定，可采用二元比较法。通过二元比较来对m个目标的“重要性”进行定性排序。首先，对目标集中的pk与pl作二元比较:

pk＞pl，排序标度ekl= 0.0，elk= 1.0

pk= pl，排序标度ekl= 0.5，elk= 0.5

pk＜pl，排序标度ekl= 1.0，elk= 0.0

然后，根据上述条件，创建矩阵E，E称为目标集二元比较重要性排序标度矩阵。

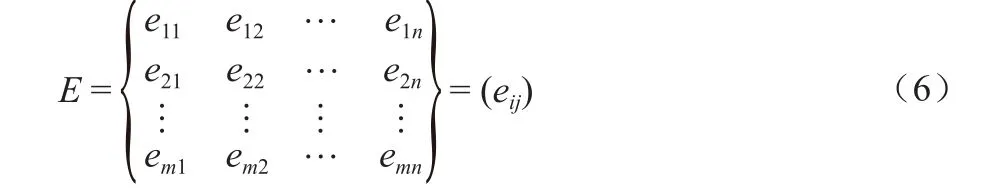
满足:①ekl仅在0.0，0.5，1.0中取值；②ekl+ elk=1.0；③ekk= ell= 0.5。

再将权向量w归一化，得到归一化的目标集权向量w ′。

求得样本集的权向量以后，就可以求出相应的样本对于优的隶属度。设样本j对于优的相对隶属度为uj。

（1）令α = 1，p = 1，由于海明距离为绝对值距离，= (1 - rij)，式（7）变为模糊综合评判模型:

（2）令α = 1，p = 2，式（7）变为TOPSIS理想点模型:

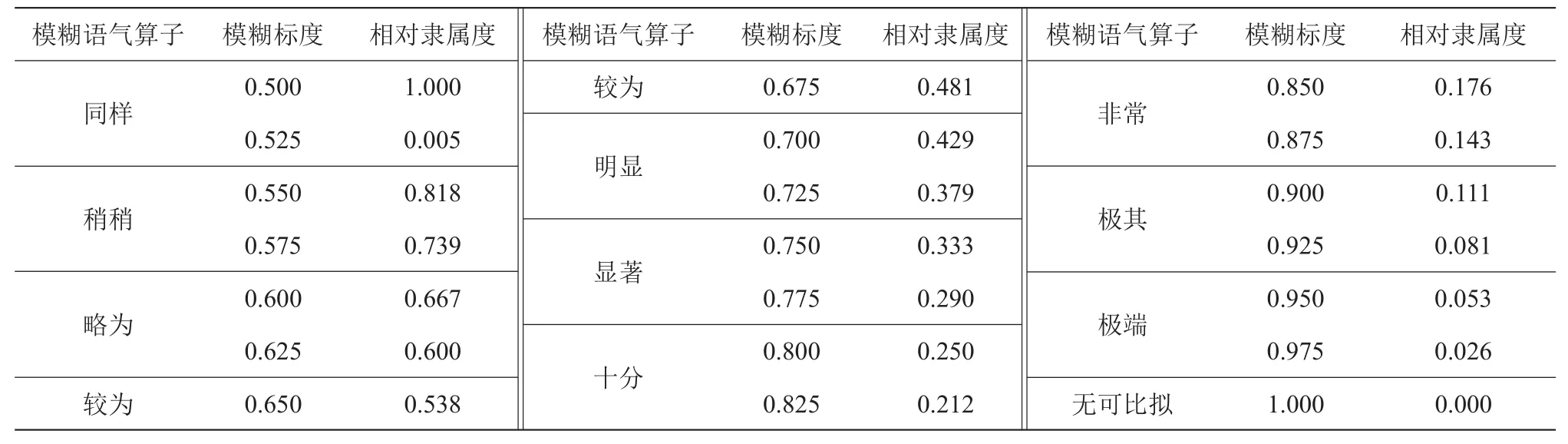
表1 模糊语气算子与模糊标度、相对隶属度关系表

（3）令α = 2，p = 1，式（7）变为在文献[8]中给出的描述神经网络系统中神经元的激励函数模型:

（4）令α = 2，p = 2，式（7）变为在文献[9]中给出的模糊优选模型:

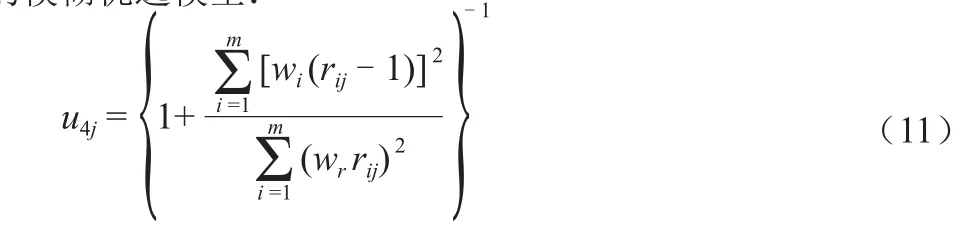
由式（8）～（11）表示的 u1j、u2j、u3j、u4j的含义为由（1）～（4）组模型参数求得的相对优属度。根据优属度的大小，可以判断目标m的优劣性[8，10]。

3 实例研究

文献[11]从一种广义的投入产出角度定义水资源配置，在给出水资源配置的基本投入产出指标后，探讨应用GEM（Group Eigenvalue Method，群组特征根法）MAUT（Multi -Attribute Utility Theory，多属性效用理论）模型对配置方案的相对有效性进行评价。

文献[11]将评价指标分为投入和产出2部分，整体考虑水资源配置涉及到人 — 生态环境 — 社会经济这一巨系统的不同子系统。投入部分选择指标为配置的经济成本（ec）、环境生态成本（eec）、随机成本（uc），其中经济成本主要考虑水资源的调配运输费用、水权水市场交易成本，环境生态成本主要考虑水资源调出区水量减少付出的环境生态代价，随机成本主要考虑配置过程的不确定性。产出部分选择指标为单方水国内总产值（c1）、区域GDP增长率（c2）、环境生态用水比例（c3）、河流水质达标率（c4）、水资源配置满意度（c5）、科技进步贡献率（c6），其中经济效益指标c1、c2依据历史用水量与GDP关系计算，环境生态指标c3依据调配水量确定、c4依据水量与水质关系确定，社会效益指标c5、c6依据调入水量保证率计算。

为方便对本文方法及研究结果的验证与比较，本文直接引用文献[11]的应用算例进行实例研究。文献[11]共设置5个方案进行对比（见表2）。

表 2 各方案的评价指标值表 [11]

表2中各方案表示不同水资源配置方案的定量结果，由于水资源配置方案的复杂性、多目标特征，所以各方案水资源配置侧重点不同。方案1、方案2的投入指标较大，经济、环境和随机成本之和分别为200万，205万元；方案3至方案5的投入指标较小，3个成本之和分别为185万，170万，165万元；产出指标中经济效益指标方案3较好，环境生态指标方案4较好，社会效益指标方案2较好。这也说明需要考虑多目标的方法对各方案进行综合评价。

3.1 建立相对隶属度矩阵

建立指标特征值矩阵:

由表2可知在9项中越大越优型指标6项，越小越优型指标3项，故应用混合型指标的相对优属度式（2）、式（3），对矩阵X进行规格化，得到指标相对隶属度矩阵:

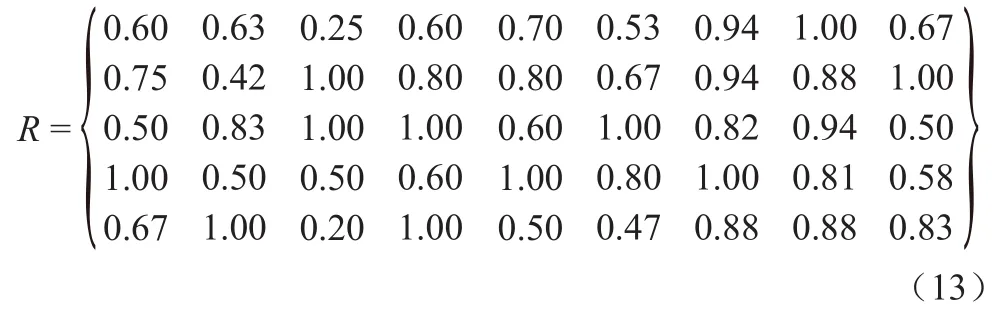
3.2 确定权向量

为了比较，引用文献[11]中专家打分确定的指标权向量:

3.3 计算优属度

令α = 1，p = 1，计算可得:

u1j= (0.68，0.81，0.80，0.76，0.73)

令α = 1，p = 2，计算可得:

u2j= (0.66，0.76，0.75，0.72，0.69)

令α = 2，p = 1，计算可得:

u3j= (0.81，0.95，0.94，0.91，0.88)

令α = 2，p = 2，计算可得:

u4j= (0.80，0.91，0.90，0.87，0.84)

4组参数的平均值:

4 结 语

本文对5个方案评价的排序结果为:方案2＞方案3＞方案4＞方案5＞方案1，与文献[11]的评价结果方案2＞方案4＞方案1＞方案5＞方案3比较虽然方案优劣排序有一定的差别，但最优方案一致，均为方案2。可以得出，可变模糊优选模型计算简便，且能为水资源配置决策层提供建议与支持。与ANN、DEA等评价方法相互参照、互为借鉴。加快水资源配置评价体系的形成。因而，在实际领域具有较广泛的应用价值，尤其在工程优化、管理评价等领域。且可变模糊集方法理论严谨，计算简便，评价结果客观、精确，符合实际情况。