二维地表水动力模型与SWMM耦合研究及应用

王自明，查良瑜，王 斌

（浙江省水利河口研究院，浙江 杭州 310020）

1 问题的提出

城市雨洪的计算主要涉及产流计算、汇流计算以及地下管网水力计算[1-2]。目前对于产汇流的计算主要有2种途径:一种是采用水文学方法；另一种是水动力方法。水文学方法多将汇水区域当做黑箱或者灰箱系统，建立输入和输出之间的关系以模拟坡面流[3]，其中较为代表的有SWMM[4]、Info Works CS[5]等。传统水文学方法所建立的城市雨洪模拟多数应用于城市规划和设计阶段，具有模型轻量、计算速度快的特点，但在实际城市内涝模拟中难以表征地表涝水产生的过程和机理，模拟精度有限。水动力学方法直接通过求解二维浅水方程来表征地表水流产汇流的物理过程，可为对城市内涝产生过程、机理等方面的研究提供更直观有力的支撑，具备更高的科研与使用价值。

但由于城市的复杂性，高精度的城市雨洪模型容易造成数值算法的不稳定且计算耗时太长，实用性较差。解以扬[6]等以基于无结构网格上二维水力学模型为主体结构，利用不同方法预报的降雨量作为系统的降雨边界条件以及模拟城市排水系统产生的结果作为控制方程中连续方程的汇源项驱动涝灾的形成和发展，但模型只用了2 281、678、646个网格对天津、南京、南昌3个大城市进行离散，模型简化程度较大，难以表征楼房、道路等构筑物的小尺度地形特征。与此同时，多数使用地表二维水动力模型模拟城市内涝的研究中，往往忽略地下管网对内涝产生的影响或简单地采用水量扣除法概化管网对地表涝水的汇集与排除功能。近年来出现的一、二维耦合计算模型如MIKE -SWMM等，具备了一定耦合计算二维坡面产汇流和管网非恒定流的能力，但其精度和稳定性难以匹配城市洪涝模型复杂的下垫面条件，且冗长的计算时间难以满足城市内涝预警、实时展现等更复杂应用的需求。

本文构建了高精细化、稳定性能好的城市二维计算模型，通过引入GPU并行计算技术，解决了地表水动力模块的计算时间问题；同时耦合SWMM的地下管网计算结果作为地表连续方程的源汇项，建立更为准确的城市内涝模型，并将该模型应用于东南某城镇区域的内涝计算和预报工作。

2 地表二维水动力模型

文中使用的高性能高分辨率的二维水动力模型，可以直接在城市的高分辨DEM上进行模拟计算，为解决传统模型在复杂地形条件下计算时间步长小，容易发散等问题，程序中将底坡源项作为单元界面上的通量，以便于达到全稳条件，对摩阻源项采用半隐式算法，大大提高了模型的稳定性。同时为解决在高分辨DEM上计算耗时较长的问题，模型中采用GPU加速技术，根据GPU和CPU构造的不同，模型基于CUDA语言给GPU和CPU分配了不同的任务。GPU的计算任务主要为通过MUSCL线性插值以及HLLC近似黎曼解分别获取单元体在预测步和校正步的单元界面通量，其并行计算能力可以同时完成多个单元体的通量求解过程；CPU负责模型的主程序，它的主要任务是利用GPU求解得到的界面通量对单元体的水深、流速等水力特征量进行迭代计算。GPU和CPU的协作运算，保证模型可以高效完成整个求解过程。模型的基本方程如下:

二维浅水方程，在地形复杂条件下无法保持内力项与源项之间的平衡。为严格保持平衡并保证涉及复杂地形模拟计算时的精度，采用如下改进形式的控制方程[7]:

式中:η为水面高（m）；η=h+zb，h为水深（m）；zb为河床高程（m）；t代表时间（s）；x，y分别代表平面2个方向的坐标（m）；u，f，g，S分别代表包含着流体变量，x方向通量，y方向通量以及源项的矢量；q是考虑降雨等因素的点源项；u，v代表x，y方向的速度（m/s）；分别代表x、y方向上底床斜率；Cf代表着底床糙率系数。浅水下河床地形示意见图1。

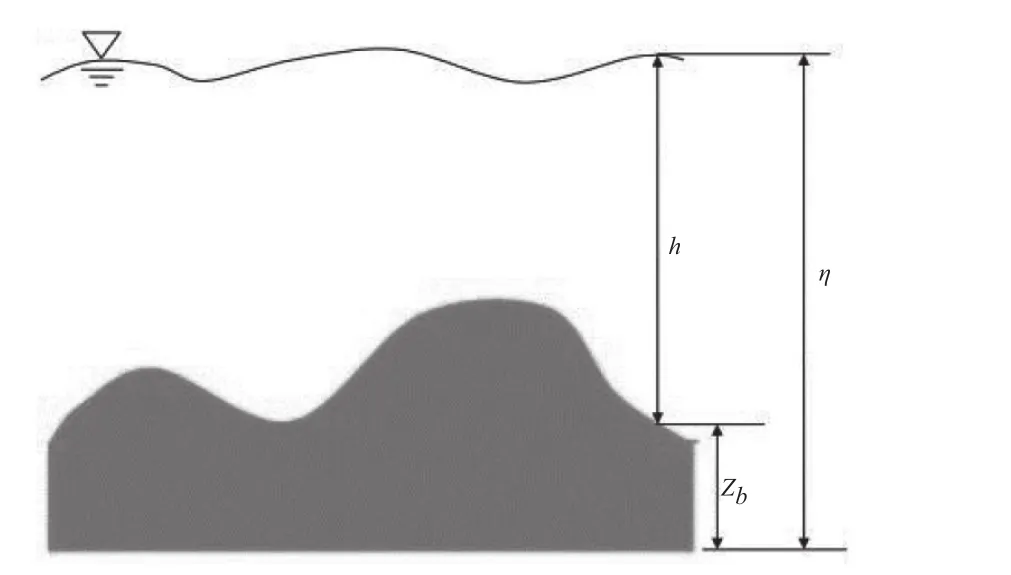
图1 浅水下河床地形示意图

模型使用Godunov型有限体积法求解上述控制方程。借助2步MUSCL - Hancock和龙格库塔方法来保证其空间和时间的二阶精度。自适应时间步长，即借用CFL条件，由CFL条件确定的时间步长为:

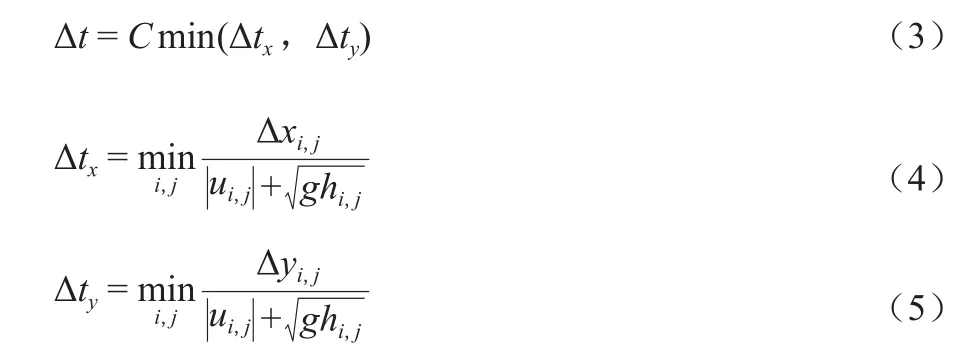
式中:C为Courant数，取值在（0，1）之间，通常建议C 值设为 0.5 ～ 0.8。

3 地表及SWMM耦合

地表二维水动力模型与SWMM模型耦合计算的示意见图2，其中二维模型使用的是正方形网格，网格编号顺序为从左下角开始逐列从下到上所有的有效网格见图3。网格左下角为坐标原点，因此可以根据点坐标以及正方形网格的大小，将点索引到二维模型所在的网格编号中。此外地表模型中通过2个文件来与地下管网模型来进行数据交换，一个是网格编号及源汇文件名的mask.dat文件，文件中包含2列信息，分别为网格编号以及对应源汇文件名称，如网格编号10对应的源汇文件名称为1.dat；另一个是每个管网节点的源汇项文件，给出源汇强度的时间序列如网格编号10读取的即为文件名为1.dat所对应的源汇强度的时间序列。由此只需提取出SWMM模型中各个管网节点的溢流强度随时间变化即可将地表二维与SWMM模型耦合起来。

SWMM生成的结果文件是一个二进制文件，其中保存每个对象在输出步长中各水力要素的结果，因此在读取结果时需要调用动态链接库中的GetSwmmResult（iType，iIndex，vIndex，period，Value）函数，其中iType为结果中的对象类型（0 - 子流域，1 - 节点，2 - 管线，3 - 系统）；iIndex为被查询对象的序号；vIndex为对应iType的不同水力要素的结果，分为子流域、节点、管网，其中与地表二维模型交换过程中较为关注的为节点的变量，包括:0 - 节点底部高程以上的水深，1 - 水头，2 - 蓄滞量，3 - 横向入流，4 - 总入流，5 - 淹没溢出流量，需要与地表维进行交换的数据主要为5 - 淹没溢出流量；period为查询时刻；Value为查询结果的返回值，可得到相应的溢流强度随时间变化的文件，完成模型耦合。

一般情况下，地下管网的出流作为地表水的内边界，需要通过水力学计算公式如（堰流公式）得到。为了在不修改地表水模型的前提下实现二者的耦合，对此过程进行一定的概化处理。认为管网计算得到的每个节点流量，只在二维模型所在的一个单元格上释放，再将流量通过换算成该单元格的降雨量，因此最终以降雨的形式，将二者耦合。如管网节点的出水量为0.01 m3/s，单元格的面积为1 m2，则认为该单元格上的降雨强度为0.01 m/s。

图2 地表模型和管网模型耦合示意图

图3 网格编号示意图

4 耦合模型的应用

某城镇地区，三面环山一面朝海，地势总体东北高，西南低，呈簸箕状，城镇下垫面类型复杂，同时拥有居民区、水库、农田、河道以及外海等不同的区域，区域总面积约25 km2。模型研究范围见图4。研究区域具有明显的海洋性气候特征，8月中旬至9月为多雨期，期间雨量的多少受台风影响较大。利用耦合模型对该区域在2009年“莫拉克”台风期间的城市内涝情况进行模拟。其中，地表水动力模型所采用的网格直接由ArcGIS的栅格文件导出，其网格大小为3 m×3 m。管网主要分布于主城区的2条主干道上，其余区域管网较少，共分布有管网节点660个，其网格DEM见图5。降雨强度见图6。

图4 研究区域图

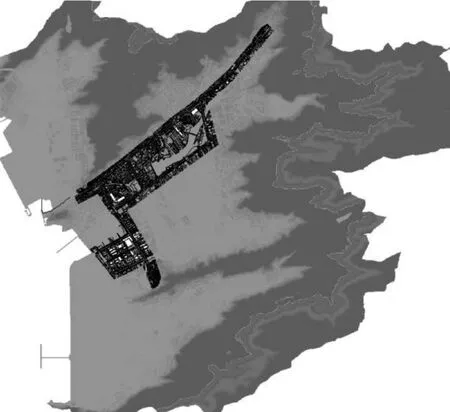
图5 地表模型 DEM 及管网示意图

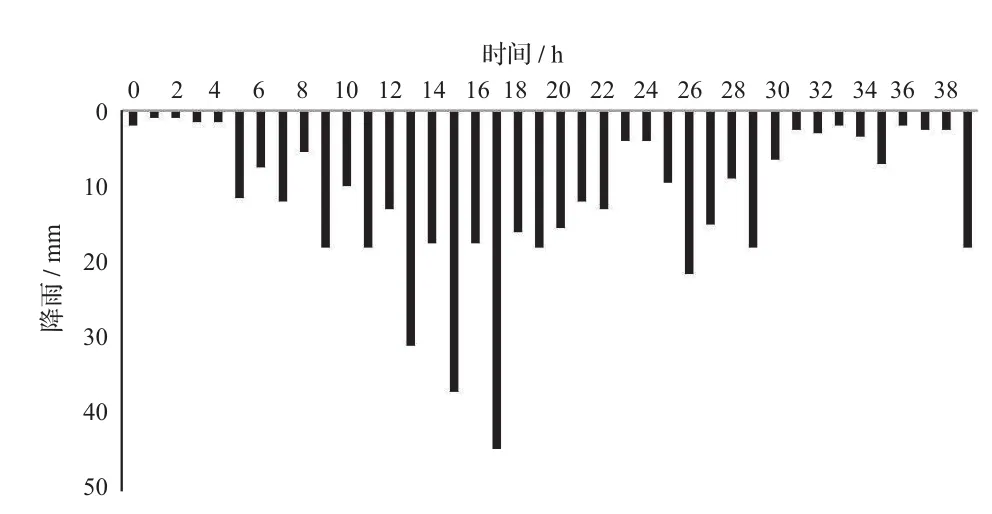
图6 “莫拉克”期间降雨强度图

二维模型中，完全采用水动力方法模拟地表产汇流过程，图7为计算流域内水流向水库汇集的过程图。实际调查中该城镇老城区暴雨时内涝较为严重，采用耦合模型对图5中老城区进行模拟计算，结果见图8，模拟产生的老城区受淹范围与调查情况基本一致，区域内积水深度50 ～ 100 cm，与实际调查结果也较为接近。

图7 产汇流过程图

图8 老城中的淹没范围及水深图

分析老城区造成积水的原因主要有以下几个方面:①地势低洼；②城市建设导致原先的河道被大量占用甚至完全填埋（见图9），上游山区河道保留较好，到达城区后，河道变为暗渠，且河道宽度和深度急剧减小，造成城区道路及房屋受淹较为严重； ③城区道路中排水管网系统薄弱，造成暴雨后雨水无处可排。

图9 河道侵占造成城区淹没图

5 结 论

本文采用高性能二维模型对城镇区域房屋、道路、河流等进行精细化的模型，同时建立SWMM管网模型，将二者耦合起来，并将计算与实际现场调查的淹没范围及水深情况进行对比。结果表明，耦合模型基本可以对城镇的内涝情况进行准确的捕捉。同时采用数据交换的方式将二维模型与SWMM模型耦合起来的方法无时间尺度问题，数据交换方便，可以为相似的工程提供借鉴。