地下水污染监测井优化设计及污染源识别
张双圣 刘汉湖 强静 刘喜坤 朱雪强


摘 要:在地下水污染源識别过程中,针对监测井监测值信息量不充分或监测值与模型参数关联性较弱的问题,提出一种基于贝叶斯公式与信息熵的监测井优化方法. 构建二维地下水溶质运移模型,并运用GMS软件进行数值求解. 为减少监测井优化设计及污染源识别过程中反复调用数值模型的计算负荷,采用克里金法建立数值模型的替代模型. 以信息熵作为优化指标,筛选出不同监测类型的最优监测方案,并以监测成本和反演精度为参考因素,选定相应监测方案,最后运用差分进化自适应Metropolis算法进行污染源识别. 算例研究表明: 7口监测井的克里金替代模型的决定系数均大于0.98,可较好地替代原数值模型. 基于监测成本最小的方案1(3号单井),其信息熵为12.772;兼顾监测成本和反演精度的方案2(井(2,3)组合),其信息熵为9.723;基于反演精度较高的方案3(3井(2,3,5)组合),其信息熵为9.377.方案1到方案3参数后验分布范围及标准差均逐渐减小,验证了信息熵是参数后验分布不确定性的有效量度.
关键词:监测井优化;污染源识别;贝叶斯方法;信息熵;最优拉丁超立方抽样;差分进化自适应Metropolis算法;克里金
中图分类号:X523 文献标志码:A
Optimization Design of Groundwater Pollution Monitoring
Wells and Identification of Contamination Source
ZHANG Shuangsheng1,3,LIU Hanhu1,QIANG Jing2,LIU Xikun3,ZHU Xueqiang1
(1. School of Environment Science and Spatial Informatics,China University of Mining and Technology,Xuzhou 221116,China;
2. School of Mathematics,China University of Mining and Technology,Xuzhou 221116,China;
3. Xuzhou City Water Resource Administrative Office,Xuzhou 221018,China)
Abstract: In the process of identifying groundwater pollution sources,a monitoring well optimization method based on Bayesian formula and information entropy is proposed for the problem that the monitoring value of monitoring wells is insufficient or the correlation between monitoring values and model parameters is weak. The two-dimensional groundwater contaminant transport model was numerically solved by GMS software. To reduce the computational load of the numerical model repeatedly in the optimization design of the monitoring wells and the identification process of the pollution source, the Kriging method was used to establish the surrogate model of the numerical model. As an optimization index, the optimal monitoring schemes of different monitoring types were selected, and the monitoring cost and inversion accuracy were taken as reference factors for the corresponding monitoring schemes. Then, the differential evolution adaptive Metropolis algorithm was used to identify the pollution source. The case study results show that: The determination coefficient of the Kriging surrogate models of the 7 monitoring wells was greater than 0.98, which indicated that the Kriging surrogate models can well replace the original numerical model. The scheme 1(single well No. 3) based on the lowest monitoring cost has an information entropy of 12.772;The scheme 2 (the combination of well No.2 and No.3) taking the monitoring cost and inversion accuracy into account has an information entropy of 9.723;The scheme 3(the combination of well No.2,3 and 5) with higher inversion precision has an information entropy of 9.377. Both the posterior distribution ranges and the standard deviation of model parameters from scheme 1 to scheme 3 were gradually reduced, which verifies that the information entropy is an effective measure of the uncertainty of the posterior distribution of the parameters.
Key words: monitoring well optimization;contamination source identification;Bayesian approach;information entropy;optimal Latin hypercube sampling;differential evolution adaptive Metropolis algorithm;Kriging
地下水污染具有隐蔽性、发现滞后性及修复难度大、费用高的特点,能否准确地得到污染源的相关信息,对于地下水污染的治理具有重要的现实意义.地下水污染源识别反问题是指通过建立地下水溶质运移模型,利用监测井处的污染物浓度监测值反求污染源位置、污染源释放强度及释放时间等信息. 由于建设监测井成本高昂,且存在监测数据包含的信息量不充分或者监测值和未知参数的关联性较弱的问题,需要对现有监测方案进行优化设计.通常以信噪比(Signal-noise Ratio,SNR)[1],基于贝叶斯公式的相对熵[2-3]作为监测井方案信息量的量度指标.信噪比仅考虑监测误差对监测数据的干扰影响,相对熵未考虑参数先验分布对后验分布的影响.为此引入信息熵概念[4],信息熵是信息不确定性的度量,不确定性越大,信息熵越大.
地下水污染源识别的求解方法主要包括贝叶斯统计方法[5-6]、地质统计学方法[7],微分进化算法[8]、遗传算法[9]和模拟退火算法[10]等. 其中,贝叶斯统计方法应用较为广泛,在运用该方法对模型参数进行反演识别时,经常需要求解参数的后验估计值或者后验分布,在参数维数不是特别高时可以采用数值积分或者正态近似的方法求解[11]. 但是,随着参数维数的增加,数值积分算法的计算量将呈指数增长,
求解过程复杂而且难度较大,往往需要借助独立抽样的蒙特卡罗方法(Monte Carlo 方法,简称MC方法)[12]进行近似求解,其中马尔科夫链蒙特卡罗方法(Markov chain Monte Carlo方法,简称MCMC方法)[13-18] 作为一种经典抽样方法得到广泛应用. 近些年,比较流行MCMC算法主要包括经典Metropolis算法[13-14]、延迟拒绝算法(delayed rejection ,DR)[15-16],自适应Metropolis算法(AM)[17],延迟拒绝自适应Metropolis算法(DRAM)[18]等. 但是这些算法均是单链MCMC算法,容易出现反演结果不收敛,或者局部最优的问题.多链MCMC算法适用于参数维度高,有多个局部最优值点,搜索量大的参数空间,能够更好地解决Markov chain局部收敛的问题[19]. 常用多链MCMC算法有DE-MC算法(Differential Evolution Markov Chain)[20],DREAM算法(Differential Evolution Adaptive Metropolis)[21]等. DREAM算法是DE-MC
算法的改进版本,相比于DE-MC算法,DREAM算法采用自适应随机子空间采样技术及能够自适应调整的交叉概率,并且运用IQR统计方法去除无用链,这几个方面提高了DREAM算法的搜索效率和解的精度[21].
此外在监测井优化设计及污染源识别过程中需要多次调用地下水溶质运移数值模型,计算代价非常高,而替代模型的应用能够有效地减少计算量.常用构造替代模型方法有多项式回归法[22]、径向基函数法[23-24]、人工神经网络法[25]、克里金法(Kriging)[26-28]等,其中Kriging法作为多项式回归分析的一种改进方法,包含多项式和随机过程两部分,同时具有局部和全局的统计特性,是一种监督式学习算法. 而且在MATLAB软件中可用专门的DACE工具箱[29]建立Kriging替代模型,方便实用,因此得到广泛应用.
综合上述研究进展,本文建立二维地下水溶质运移数值模型,在确定初始监测时刻,监测间隔时间及监测次数条件下利用最优拉丁超立方抽样方法及Kriging法建立数值模型的替代模型,以信息熵为评价指标分别计算不同监测类型下的最优监测井方案,并筛选出兼顾监测成本与监测精度的监测方案,然后以筛选出的监测方案运用DREAM算法进行污染源识别,为地下水污染源识别及监测方案优化研究提供借鉴.
1 研究方法
1.1 贝叶斯公式
贝叶斯公式如下:
在实测数据d固定的条件下,式(5)是关于参数α的函数.通过积分求解参数α的后验分布很难得出显式表达式,本研究采用MCMC (Markov Chain Monte Carlo)算法[21]对式(5)的后验分布进行求解.
1.2 基于贝叶斯公式与信息熵的监测井优化设计
监测方案Monitoring Proposal (MP)的优化设计主要包括对监测井的数量、位置以及监测频率的優化.假设初始监测时间为t1(固定值),由监测方案MP所得监测值仍记为d,此时贝叶斯公式可以改写成:
运用污染物浓度监测值d反演未知参数α,α后验概率密度函数p(α|d,MP),α的后验分布的信息熵类似定义如下:
式(10)左端项含有监测值d,但在进行监测井方案设计时,并未真正得到d,可认为监测值d是随机变量,其概率密度函数为p(d|MP). 为了得到一个仅包含监测方案MP的函数,对式(10)两侧乘以
p(d|MP),再对d积分,求出信息熵H(MP,d)的期
望为:
式(11)中E(H(MP,d)只受到监测方案MP的影响,可简记为E(MP). 通过求解E(MP)的最小值,就可以获得最优监测井设计方案MP*.根据信息熵概念,利用由MP*获得的污染物浓度监测值d*反演未知参数α,此时α后验分布的信息熵最小,表示 α的不确定性也最小,反演效果最优.
因此,只要监测设计方案MP固定,通过式(12)(14)(15)就可以得到此种监测方案的信息熵近似值.
1.3 DREAM算法
1.3.1 DREAM算法具体步骤
DREAM算法[21]是在DE-MC算法[20]的基础上提出的. DREAM算法步骤如下:
1)在模型未知参数α先验范围内随机产生NP
个初始样本Xi(t)=(Xi,1(t),Xi,2(t),…,Xi,m(t))T(i=1,2,…,NP,t=0),作为NP条马尔科夫链的起始点.
2)针对第i(i = 1,2,…,NP)条马尔科夫链,运用DE方法产生参数的变异样本Zi(t).
式中: I表示m阶单位矩阵;e表示m阶方阵,其对角线上元素服从均匀分布U(-b,b),b为自定义的极小值;δ表示用于产生候选样本的平行链数的二分之一,r1(j),r2(k)∈{1,2,…,NP}为随机选取的平行链编号,且当j,k = 1,2,…,δ 时,r1(j)≠r2(k)≠i;
γ(δ,d′)为比例因子;ε 表示m维向量,其m个元素均服从正态分布N(0,b*),b*为自定义的极小值.
3)引入交叉概率Cr,交叉混合Xi(t)和Zi(t)得到候选样本Vi如下:
对?坌i∈{1,2,…,NP},当j = 1时,令d′ = d;对j = 1,2,…,m,有
Xi,j(t) = Xi,j(t) if U≤1 - Cr,d′ = d′ - 1Zi,j(t) 其他 (17)
其中0≤Cr≤1,U是区间[0,1]上的随机数.
5)根据IQR统计方法[21]去除无用链.
6)判断收敛性.如果马尔科夫链满足Gelman-Rubin收敛准则[30],若满足条件则计算终止,否则继续进化平行序列.
1.3.2 DREAM算法的收敛性判断
本文采用Gelman-Rubin收敛诊断方法[30]对
DREAM算法后50%采样过程的收敛性进行判断,判断指标为:
1.4 最优拉丁超立方抽样方法和Kriging替代模型
1.4.1 最优拉丁超立方抽样方法
拉丁超立方抽样是一种多维分层随机抽样方法,但抽样结果有很大地随机性,每一次抽样得到的结果差别很大.假设要在m维参数α取值范围[0,1]m内运用拉丁超立方抽样方法抽取q组样本,q组样本数据用矩阵Φqm表示;符合要求的矩阵Φqm共有(q!)m种,总共可以得到(q!)m种拉丁超立方抽样方案,(q!)m种抽样方案Φqm组成的集合记为?撰.这些抽样方案对整个抽样空间的覆盖填充程度有很大地差异[28]. 本文运用中心化L2偏差[31]作为优化指标寻求覆盖填充程度最优的抽样方案,中心化L2偏差表达式如下:
1.4.2 Kriging替代模型
Kriging法[26]是由Matheron等人发明的一种优化插值方法,其具体工作原理可查阅文献[27],基本步骤如下:
Kriging替代模型响应值y与自变量k之间的关系可用下式表示:y(k) = f T B + Z,式中k∈IRmk (mk表示自变量k维数),f(k)=(f1(k),f2(k),…,fp(k))T,其中fi(·)(i = 1,2,…,p)表示事先确定的多项式函数,常常是0阶,1阶或者2阶多项式;β = (β1,β2,…,βp)T为待定参数;Z为误差随机变量,E(Z) = 0,Var(E) = σ2.
2002年,Lophaven等人[29]基于Matlab平臺创建了DACE工具箱,用于生成Kriging替代模型,本文中Kriging替代模型的建立就是基于此工具箱.
2 算例应用
2.1 模型建立及问题概述
2.1.1 模型建立
假定研究区域为矩形区域,长1 000 m,宽600 m,含水层为厚度35 m的砂质潜水含水层(水文地质参数见表1),西部边界Γ1与东部边界Γ3为给定水头边界,其中东部水头为25 m,西部水头为30 m,北部边界Γ2与南部边界Γ4为隔水边界.天然状态下地下水流为自西向东流动的二维均质各向同性的非承压稳定流.
研究区内共有7眼监测井,地下水水质背景值较好,含水层污染物的初始浓度为零,某日研究区下游发现污染物X,初步断定污染源S在上游的某一区域范围(先验范围)内,且在某时间段内以注水井的形式(200 m3/d)持续恒定地向含水层中排放污染物. 研究区平面示意图如图1所示.
以西南角为坐标原点建立坐标系,根据研究区水文地质条件,建立地下水水流数值模型:
式中:Dx、Dy分别为水动力弥散系数在x、y方向上的分量,m2/d;vx、vy分别为x、y方向上地下水的渗流速度,m/d;n为含水层介质的孔隙度,无量纲;c为污染物质量浓度,mg/L;Qinj为向含水层的注入液体量,m3/d;Cinj为随液体进入含水层的污染物质量浓度,mg/L;f(x,y,t)表示仅在水动力弥散作用下,单位时间通过实际过水断面单位面积的溶质质量.
建立的地下水水流及溶质运移模型运用GMS软件中的MODFLOW和MT3DMS模块进行计算求解. 为保证每个网格中心对应一个潜在污染源(污染源样本)的位置,将研究区域剖分为150行200列的正方形有限差分网格,基本单元格边长为4 m.
2.1.2 问题概述
针对潜在的污染源范围,要求在现有7眼监测井的基础上,制定优化的监测井方案,以此进行污染源的識别(包括污染源的位置,污染物投放和结束时间,以及污染物的投放质量浓度),即求解污染源未知参数α = (Xs,Ys,T1,T2,Cs),其中(Xs,Ys)为污染源位置,m;T1、T2分别为污染源开始排放和结束排放的时刻,d;Cs是注入污染物的质量浓度,mg/L.表2为7眼监测井的坐标位置.
以未发生污染某确定时刻作为初始时间,此时t=0.要求从第750 d至第900 d内完成污染源识别任务(期间每10 d进行一次监测,每眼井共监测16次),假设上述5个参数的先验分布为均匀分布α = (Xs,Ys,T1,T2,Cs)5个待求参数的先验范围分别
如下:
60 m≤Xs≤220 m,240 m≤Ys≤400 m,8 d≤T1≤12 d,18 d≤T2≤22 d,2 800 mg/L≤Cs≤3 300 mg/L.
2.2 Kriging替代模型的建立
1)运用最优拉丁超立方抽样方法从污染源未
知参数α的先验范围内抽得均匀分布的100组参数作为Kriging替代模型训练输入值(此时CL2(Φ100,5)=0.002 462),如表3所示.
2)分别对7眼监测井建立Kriging替代模型. 将表3中100组参数分别代入GMS软件中,得到7眼监测井不同监测时间点的污染物浓度值,作为
Kriging替代模型输出值.将100组输入值与输出值作为训练样本代入MATLAB软件,利用DACE工具箱对各监测井的Kriging替代模型进行训练.
在未知参数的先验范围内运用拉丁超立方抽样方法重新得到10组参数作为检验样本的输入值(表4),再次代入GMS软件中,得到7眼监测井不
以7号监测井为例,以检验样本的输出值作为横坐标,替代模型的输出值作为纵坐标,绘制替代模型输出值与检验样本输出值的对比图(图2). 由图2可知,数据散点均集中分布于y = x直线上,表明替代模型可较好地对数值模型进行替代.
为进一步检验替代模型的精度,分别运用决定系数,平均绝对误差及均方根误差3个指标对7眼监测井的替代模型进行检验评价,结果如表5所示.
由表5数据可知,Kriging替代模型预测精度较高,且7眼备选监测井平均绝对误差的平均值为0.14,平均决定系数R2 = 0.996 8. 在参数反演及监测井优化问题中,由于运用Kriging替代模型,整体误差包括替代模型误差及测量误差. 假设第i(i=1,2,…,7)眼备选监测井的Kriging替代模型误差εi′满足正态分布N(0,(σi′)2),且均值E(εi′)=0,均方差σi′ =RMSEi;假设测量误差ε″满足正态分布N(0,(σ″)2),且均值E(ε″) = 0,均方差σ″ = 0.01. 由于替代模型误差εi′及测量误差ε″相互独立,故第i(i=1,2,…,7)口监测井整体误差εi = εi′ + ε″满足正态分布N(0,(σi′)2+(σ″)2),据此可以确定1.1节中式(4)和式(5)中协方差矩阵C(ε).
2.3 监测方案优化设计
7眼井可得到7组监测数据,任取i(i=1,2,…,7)组监测数据作为参数反演的监测数据d,共有Ci7(i=1,2,…,7)种组合形式,每种组合形式代表一种监测方案,从而监测方案共有Ci7(i=1,2,…,7)种. 由于i=1,2,…,7,按照选取的监测井数量进行划分,监测类型共有7类. 根据1.2节可知,每类监测方案优化问题其实就是在Ci7(i=1,2,…,7)种监测方案里面选取信息熵最小的监测方案,信息熵最小的监测方案可视为最优监测方案. 问题可概化如下:
min E(MP) = -ln p(α) + min U(MP) (19)
式中:MP表示监测方案.
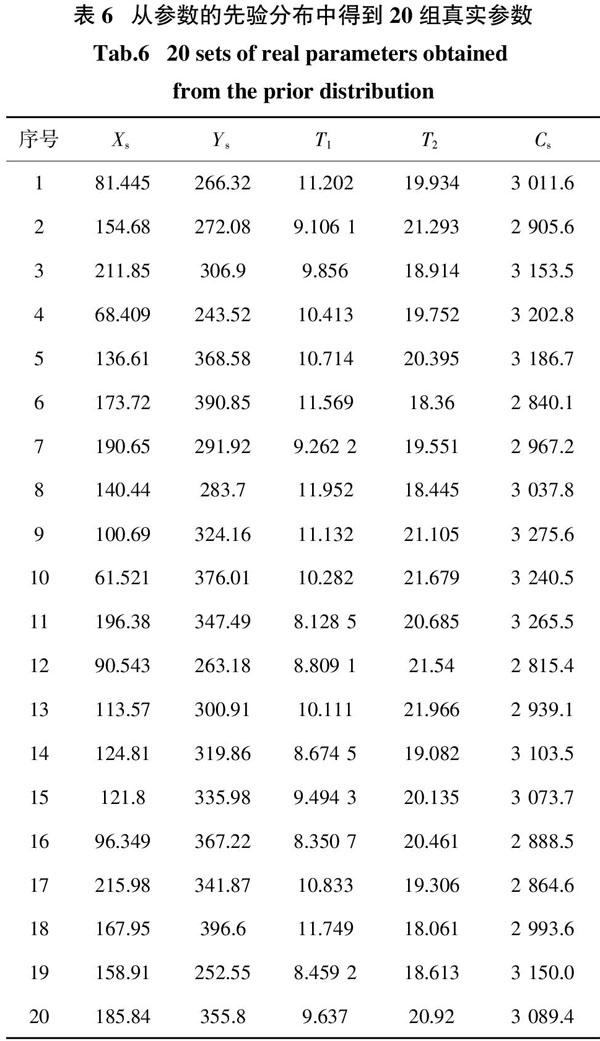
根据式(12)(14)(15)分别求得不同监测方案的信息熵E(MP).为了验证基于贝叶斯公式与信息熵的监测井优化设计效果,以信息熵E(MP)与反演结果相对误差均值MRE(MP)为指标对Ci7种监测方案进行评价.从参数α的先验分布里运用拉丁超立方抽样方法随机并且均匀地得到20组参数作为真实参数(表6),对应于Ci7种监测方案,20组真实参数通过Kriging替代模型产生了20×Ci7组浓度监测值.利用产生的监测值,运用DREAM算法(初始平行链数为10)反演参数α,其中每条马尔科夫链长度为12 000,在马尔科夫链长度10 000时所有参数的收敛性判断指标■<1.2.为了保证精度,只将马尔科夫链趋于稳定后的最后2 000组样本进行后验统计,得出参数后验均值估计MMP . 并将表6中的真实参数α一并代入MRE(MP)表达式,如下:
式中: j为第j组真实参数α;k表示参数α的第k个分量. 由式(20)得出Ci7种监测方案的反演结果MRE(MP),如表7所示.
分别将表7中1眼井监测方案,2眼井组合监测方案以及3眼井组合监测方案下的MRE(MP)与 E(MP)进行线性拟合,结果见图3和表8. 由于4眼井组合监测方案,5眼井组合监测方案以及6眼井组合监测方案下E(MP)数值接近,同时MRE(MP)数值也十分接近,并且考虑到计算误差的影响,不再对这3种类型监测方案下MRE(MP) 与E(MP)进行线性拟合.
由于图3(c)中决定系数R2=0.552比较小,运用 F检验对图3(c)中线性方程的显著性进行检验[32].
检验假设H0 : E(MP) 和RT(MP)之间没有真正的线性关系,H1 : E(MP)和RT(MP)之间有线性关系;显著性水平α = 0.05.
经计算可得F检验统计量F = 40.739,而Fα(1,35-2) = Fα(1,33) = 4.139,因此F > Fα(1,33),拒绝H0 . F檢验表明E(MP) 和RT(MP)之间存在线性关系. 另外图3(c)中实线表示拟合直线,两侧虚线标出其95%置信区间,只有2个点落在置信区间外面,也充分说明了E(MP) 和RT(MP)之间具有正线性关系.
综上,由图3和表8可知,MRE(MP)与E(MP)呈较好的正相关关系,说明E(MP)是参数反演结果精度的有效量度,E(MP)越小,参数反演结果精度越高. 但表7中E(MP)取得最小值的监测方案的MRE(MP)未必是最小值(如1眼监测井情况下,选取3监测方案时E(MP)为12.772,MRE(MP)为0.069;选取2监测方案时E(MP)为13.004,MRE(MP)为0.063),主要原因在于选取20组参数真值(表6)时,虽然运用拉丁超立方抽样方法使20组参数真值尽量均匀分布在参数先验范围内,但由于数据较少,无法在真正意义上均匀分布在先验范围内,而信息熵的求解运用蒙特卡洛方法(MC方法)在参数先验范围内运用拉丁超立方抽样方法抽取样本20 000次,二者相比,因此认为以E(MP)最小值作为选取最优监测方案的指标更加可信,而不能以MRE(MP)最小值作为选取最优监测方案的指标.
另由表7可知,并不是任何条件下监测井数量越多,信息熵越小,如两眼监测井情况下,(2,3)组合方式下的E(MP)为9.723,3眼监测井情况下,(1,5,6)组合方式下的E(MP)为11.666. 表7显示每种监测类型下均存在信息熵最小的最优监测井方案.因此从表7中各监测类型中筛选出信息熵最小的监测方案作为相应监测井组合方案中的最优方案,并绘制不同监测类型中最优方案的信息熵
E(MP)随监测井数量的变化曲线,如图4所示.
由图4可知,在各监测类型的最优方案条件下,信息熵随着监测井数量的增加而减小,其中两眼井的信息熵显著小于一眼井的信息熵,但是与其他数量的监测井的信息熵相差不大.
通常情况下,对于利用监测井进行污染源识别,既要考虑反演精度,又要考虑监测成本. 因此本算例选取3种监测方案进行污染源识别. 方案1:监
测成本最小的1眼监测井方案(3号单井). 方案2:兼顾反演精度与监测成本的监测井方案:由于2眼井的信息熵与3~7眼井的信息熵相差不大,但随着监测井数量的增加,监测费用显著增加,因此该方案选2眼井监测方案(监测井(2,3)组合). 方案3:基于较高反演精度的监测井方案,由于3~7眼井的信息熵相差不大,认为反演精度相近,因此该方案选3眼井监测方案(监测井(2,3,5)组合).
2.4 基于优化监测方案的污染源识别
以表6中第1组参数真值α=(Xs,Ys,T1,T2,Cs)=(81.4,266.3,11.2,19.9,3 011.6)为例,分别利用2.3节选取的3种监测方案,运用DREAM算法(初始平行链数为10,反演稳定后平行链数记为n)进行污染源参数反演,其中每条马尔科夫链长度是12 000.
由表9和图5可知,方案1到方案3参数后验分布范围逐渐减小,与相应监测方案信息熵的变化趋势一致(图4),且参数真值均在参数后验分布范围内. 进一步表明监测方案信息熵越小,参数后验分布不确定性越小.
为进一步说明3种监测方案的参数反演效果,对马尔科夫链稳定后的剩余2 000个样本点进行后验统计分析,结果见表10.
由表10可知,从方案1到方案3,5个参数的标准差均逐渐减小;方案2与方案3下5个参数后验均值相对误差数值接近,与方案1相比,Xs,Ys以及T1的后验均值相对误差均大幅减少,但是T2、Cs 2个参数的后验均值相对误差却有所增大.结合图3、图4及表10分析,进一步说明参数后验分布的信息熵与5个参数后验均值相对误差的平均值成正比,但不能保证参数后验分布的信息熵与每个参数后验均值相对误差成正比,即运用参数后验分布的信息熵作为监测井优化设计的指标,在参数整体反演精度最高的情况下,不能保证每个参数的反演效果均达到最佳.
监测井数越多所需费用越多,单井监测费用最少. 方案2与方案3信息熵差距很小,5个参数后验样本均值相对误差的平均值也近似相等,却增加了1眼井进行监测,费用明显增加. 对于本文案例,如果需要综合考虑监测成本及参数后验分布范围大小,认为方案2为最佳的监测井方案.
3 结 论
1)与拉丁超立方抽样方法相比,最优拉丁超立方抽样可有效提高参数先验分布抽样的均匀性,避免抽样结果的随机性及对整个抽样空间的覆盖填充程度的差异性.
2)Kriging替代模型属于黑箱模型,能以较小的计算量得到和地下水数值模型相近的输入输出关系,在保证模拟精度的条件下,显著降低计算负荷.
3)参数反演结果的相对均方根误差与监测方案信息熵呈现较好的正相关关系. 信息熵是参数后验分布不确定性的有效量度,信息熵越小,参数后验范围越小,基于贝叶斯公式与信息熵的监测方案优化设计方法是确定地下水污染监测方案的有效方法.
4)并非监测井数量越多越有利于污染源的反
演识别,必须以信息熵为筛选指标制定各监测类型下的最优监测井组合方案,而且可以以监测成本、监测效率、反演精度等为限制条件进行具体工况条件下最优监测方案的选择.
参考文献
[1] CZANNER G,SARMA S V,EDEN U T,et al. A signal-to-noise ratio estimator for generalized linear model systems [J]. Lecture Notes in Engineering & Computer Science,2008,2171:1063—1069.
[2] HUAN X,MARZOUK Y M. Simulation-based optimal Bayesian experimental design for nonlinear systems [J]. Journal of Computational Physics,2013,232(1):288—317.
[3] LINDLEY D V. On a measure of the information provided by an experiment [J]. The Annals of Mathematical Statistics,1956,27(4):986—1005.
[4] SHANNON C E. A mathematical theory of communication [J]. The Bell System Technical Journal,1948,27(3):379—423.
[5] SOHN M D,SMALL M J,PANTAZIDOU M. Reducing uncertainty in site characterization using bayes monte carlo methods [J]. Journal of Environmental Engineering-asce,2000,126(10):893—902.
[6] CHEN M,IZADY A,ABDALLA O A,et al. A surrogate-based sensitivity quantification and Bayesian inversion of a regional groundwater flow model[J]. Journal of Hydrology,2018,557:826—837.
[7] SNODGRASS M F,KITANIDIS P K. A geostatistical approach to contaminant source identification [J]. Water Resources Research,1997,33(4):537—546.
[8] RUZEK B,KVASNICKA M. Differential evolution algorithm in the earthquake hypocenter location [J]. Pure and Applied Geophysics,2001,158:667—693.
[9] GIACOBBO F,MARSEGUERRA M,ZIO E. Solving the inverse problem of parameter estimation by genetic algorithms:the case of a groundwater contaminant transport model [J]. Annals of Nuclear Energy,2002,29(8):967—981.
[10] DOUGHERTY D E,MARRYOTT R A. Optimal groundwater management:simulated annealing [J]. Water Resources Research,1991,27(10):2493—2508.
[11] TANNER M A. Tools for statistical inference:methods for the expectation of posterior distribution and likelihood functions [M]. Berlin:Springer,1996:14—39.
[12] ROBERTS C P,CASELLA G. Monte carlo statistical methods [M] .2nd ed. Berlin:Springer,2004:79—122.
[13] METROPOLIS N,ROSENBLUTH A W,ROSENBLUTH M N,et al. Equation of state calculations by fast computing machines [J]. The Journal of Chemical Physics,1953,21(6):1087—1092.
[14] HASTINGS W K. Monte Carlo sampling methods using Markov chains and their applications [J]. Biometrika,1970,57(1):97—109.
[15] TIERNEY L,MIRA A. Some adaptive Monte Carlo methods for bayesian inference [J]. Statistics in Medicine,1999,18:2507—2515.
[16] MIRA A. Ordering and improving the performance of Monte Carlo Markov Chains [J]. Statistical Science,2002,16:340—350.
[17] HAARIO H,SAKSMAN E,TAMMINEN J. An adaptive metropolis algorithm [J]. Bernoulli,2001,7(2):223—242.
[18] HAARIO H,LAINE M,MIRA A. DRAM:efficient adaptive MCMC [J]. Statistics and Computing,2006,16(4):339—354.
[19] 张江江. 地下水污染源解析的贝叶斯监测设计与参数反演方法 [D]. 杭州:浙江大学环境与资源学院,2017.
ZHANG J J. Bayesian monitoring design and parameter inversion for groundwater contaminant source identification [D]. Hangzhou:College of Environmental and Resource Sciences,Zhejiang University,2017. (In Chinese)
[20] TER BRAAK C J F. A Markov Chain Monte Carlo version of the genetic algorithm differential evolution:easy Bayesian computing for real parameter spaces [J]. Statistics and Computing,2006,16(3):239—249.
[21] VRUGT J A,TER BRAAK C J F,DIKS C G H,et al. Accelerating Markov Chain Monte Carlo simulation by differential evolution with self-adaptive randomized subspace sampling [J]. International Journal of Nonlinear Sciences and Numerical Simulation,2009,10(3):273—290.
[22] KNILL D L,GIUNTA A A,BAKER C A,et al. Response surface models combining linear and Euler aerodynamics for supersonic transport design [J]. Journal of Aircraft ,1999,36(1):75—86.
[23] LI J,CHEN Y,PEPPER D. Radial basis function method for 1-D and 2-D groundwater contaminant transport modeling [J]. Computational Mechanics,2003,32(1):10—15.
[24] 肖傳宁,卢文喜,赵莹,等.基于径向基函数模型的优化方法在地下水污染源识别中的应用 [J]. 中国环境科学,2016,36(7):2067—2072.
XIAO C N,LU W X,ZHAO Y,et al. Optimization method of identification of groundwater pollution sources based on radial basis function model [J]. China Environmental Science,2016,36(7):2067—2072. (In Chinese)
[25] CHRISTIE M,DEMYANOV V,ERBAS D. Uncertainty quantification for porous media flows [J]. Journal of Computational Physics,2006,217(1):143—158.
[26] MATHERTON G. Principles of geostatistics [J]. Economic Geology,1963,58(8):1246—1266.
[27] SACKS J,WELCH W J,MITCHELL T J,et al. Design and analysis of computer experiments [J]. Statistical Science,1989,4(4):409—435.
[28] 高月华.基于Kriging 代理模型的优化设计方法及其在注塑成型中的作用 [D]. 大连:大连理工大学运载工程与力学学部,2008.
GAO Y H. Optimization methods based on Kriging surrogate model and their application in injection molding [D]. Dalian:Faculty of Vehicle Engineering and Mechanics,Dalian University of Technology,2008. (In Chinese)
[29] LOPHAVEN S N,NIELSEN H B,SONDERGAARD J. Dace:A MATLAB Kriging toolbox[R]. Kongens Lyngby: Technical University of Denmark,Technical Report No. IMM-TR-2002—12.
[30] GELMAN A G,RUBIN D B. Inference from iterative simulation using multiple sequences [J]. Statistical Science,1992,7:457—472.
[31 HICKERNELL F J. A generalized discrepancy and quadrature error bound [J]. Mathematics of Computation of the American Mathematical Society,1998,67(221):299—322.
[32] 周圣武,李金玉,周长新. 概率论与数理统计[M].2版. 北京:煤炭工业出版社,2007:208—215.
ZHOU S W,LI J Y,ZHOU C X. Probability theory and mathematical statistics [M].2nd ed. Beijin:China Coal Industry Publishing House,2007:208—215.(In Chinese)

