变中抓不变 助推初中数学课堂深入本质

陈立顺

我们知道，虽然初中生的抽象思维已占主导地位，但其仍然是属于经验型的，因此初中数学课堂教学应坚持具体与抽象相结合的原则，教师要善于创设合理的情境，以激发学生的兴趣，并帮助学生合理生成和理解知识。然而，我们也看到，由于过度地依赖情境和活动，数学课堂中“去数学化”的现象却很严重.那么如何根据情境，促使学生更合理地进行归纳猜想、推理论证，从而不断将数学课堂推向深入，以更顺利地解决问题呢？其中“变中抓不变”就是一种很有效的策略和方法。下面笔者就结合平时的教学谈一些想法和做法。

一、变中抓不变 让概念抽象因凸显本质而易于生成

抽象是人类从现实进入到数学的内心活动，它是从许多事物中舍弃个别的、非本质属性，得到共同的、本质属性的思维过程。这个过程既要关注研究对象的共性，又要关注研究对象与其它事物之间的差异，这个过程也可以理解为是一个变中抓不变的过程。变化的是研究对象及其之间的差异，不变的是研究对象之间的共性。在这个过程中，教师要善于引导学生进行科学地观察，合理地归纳和猜想。

爱因斯坦曾说：“理论决定着你能观察到什么”。在概念教学时，如果学生心中拥有“变中抓不变”的思想，那么当教师将一些典型素材呈现给学生时，学生就能有意识地去观察分析这些对象的共性和差异，从而触摸到概念的本质，为概念的生成和理解奠定基础。例如，函数概念是初中数学的一个难点，若能用变中抓不变的思想来生成，可较容易地突破。教师先向学生呈现一个我国人口从1949至2011年变化的统计表，同时呈现一个人口理论计算公式和变化折线图，让学生分析我国人口变化趋势，并让学生预测10年、20年后我国将有的人口情况，以供国家领导决策，接着教师提出一个触及函数本质属性的问题：当两个变量具有什么样的关系时，才能实现由一个变量来唯一确定另一个变量的目的。在说明上面三个例子中两个变量均能够实现上述目的后，再列举一些生活中分别用图象、表格及等式表示两个变量对应关系的例子（正反例都有），让学生分析其共性和差异，从而合理抽象出函数的概念。这样教学，就能使函数概念的本质得到用变中抓不变思想来揭示概念，变化的是对象和它们的差异，不变的是不同对象的共性，也即概念的本质特征，教师要善于创设便于学生进行概念本质抽象的情境。

二、变中抓不变 让命题教学因紧扣本质而深入开展

命题是数学最基本的表达方式之一。中学数学命题教学的基本要求是：使学生深刻理解数学命题的意义，明确其推导过程和适用范围，具备灵活运用数学命题解决问题能力。命题的教学过程主要靠推理完成。在这个过程中，若能运用变中抓不变的思想，就能使命题教学紧扣本质而深入开展。我们知道，教材上展现在学生面前的定理、公式等都是经过千锤百炼完美无缺的，它略去了曲折复杂的发现过程。教师在教学时，应根据这些定理、公式的本质特征，去构建“再发现”、“再创造”的情景，以培养学生发现、创新、归纳、猜想和推理的能力。可如何构建“再发现”、“再创造”的情景，对教师是一个挑战。此时，教师若能利用变中抓不变的思想来设计，就可以收到意想不到的效果。例如三角形内角和定理的再发现，教师可创设这样的情境，用几何画板在屏幕上画出△ABC，然后固定顶点B和C，拖动点A，让学生观察△ABC各内角的变化，体验有些角变大就必然有些角要变小的现象，体验三角形的角之间是存在某种神秘关系的。由于学生小学已知道三角形内角和等于180度的事实，所以当教师问及三角形三个内角有什么关系时，学生基本会回答出答案。但教师要去追问，当初世界上第一個发现此事实的人如何发现这一规律的？当学生困惑时，教师接着启发：我们知道，世界上第一个发现三角形内角和定理的人（泰勒斯）是通过拼图发现这一规律的，今天我们要通过另一条途径来发现这一规律：现在我们让点A沿着一条与BC平行的直线上运动，看看三角形的角有什么不变的关系？这一“变中有不变”的情境创设，不仅能使学生

“再发现”三角形内角和定理的事实。而且还能从中获得该定理的证法。在教学中，运用变中抓不变思想，不仅有利于发现一些正确的结论，还经常能辨析出一些错误的结论，如数学中有些静态的图形中。两条看似相等的线段其实是无法证明相等的，这时可让图形动起来，动到一个比较特殊的位置，再观察两条线段的长短变化，这时往往结论就跃然纸上了。

命题的证明是命题教学的重要方面。教师要让学生分清命题的条件和结论及其之间的因果关系，这是本质。在证明命题时，教师要善于用变中抓不变的思想理解和应用条件，因为题目呈现在学生面前的除了已知条件外，往往还伴随有其它必然或偶然的隐含条件，教师要关于引导学生去排除一些或然条件的干扰，让学生集中精力朝正确方向找到一些必然的隐含条件，从而较快地形成证明思路。如圆周角定理的证明是初中教学的一个难点，对教材中证明过程为什么要分三种情况讨论学生更是不理解。当教师创设情境，让学生发现“圆周角的度数等于它所对弧上的圆心角度数的一半”的事实后，教师可这样启发学生探索其证明方法，在圆中，一条弧对着一个圆心角和无数个圆周角，也就是说圆周角的顶点是可以变化的，但不管位置如何变，这个结论始终是成立的，那么作为圆上的任意一点，它所隐含的必然结论有哪些？从这里能不能找到证明的突破口呢？这样启发，学生自然就想到要连接半径了，因为半径处处相等，于是问题就转化为证明学生熟悉的等腰三角形中与其顶角相邻的外角与其底角之间两倍的关系的问题了。当学生证出一种情况后，教师要顺势启发，这样证明有漏洞吗？接着教师可借助多媒体演示，让圆周角的顶点继续在弧上运动，让学生自主分析第一种情况的证法能否代表其它情况的证明，最后通过学生自主合作探究完成证明。

定理、法则的应用也是命题教学的必要环节。只有通过应用，学生才能深刻理解并掌握定理或法则。心理学研究证明，若知识在单一的背景下重复和应用，那么只会形成僵化的知识，情境一变，学生就不会了。因此，教师在定理、法则教学后一定要让其在不同情境中得到应用，让学生去体验那变中不变的规律。如学过相似三角形的判定定理后，教师可实行“一题多变”，将相似三角形的判定与双曲线、抛物线、特殊四边形及圆等知识进行组合，通过知识的不同组合来加深对知识的理解。

三、变中抓不变 让问题解决因回归本质而精准突破

数学模型是数学与外部世界联系的桥梁，在数学建模的过程中，一些非本质的，对反映客观事实影响不大的东西已被去掉，只留下本质的东西及其联系。因此模型能够适应变化。教师在引导学生解决问题时，要让学生树立变中抓不变的思想，要善于引导学生去弄通情景，把实际问题转化成数学问题，要善于抓住不变的本质特征，去寻找或构造模型。当找不到数学模型解决时，也要善于用变的观点换个角度看问题，如运用数形结合将代数领域问题映射到几何领域中去解决等等。如下例，若能用变中抓不变的思想来思考，就很容易找到模型加以突破。

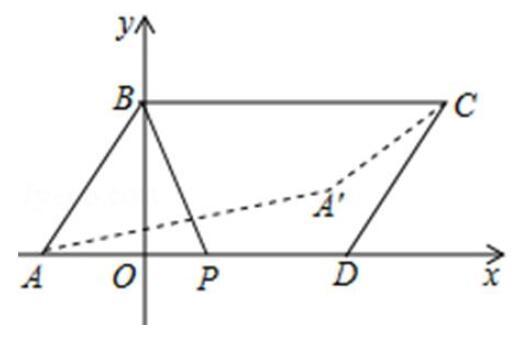
已知，在平面直角坐标系中，平行四边形ABCD的坐标分别为A（-1，0）、B（0，2）、C（3，2）、D（2，0），点P是AD边上的一个动点，若点A关于BP的对称点为A'，试求A'C的最小值。

分析 这个问题一些学生可能会想到用三角形两边之差小于第三边的模型来思考。但若能用变中抓不变的思想来分析，则更易理解和突破。由BA′=BA=5

可知，当点P在AD上运动变化时，点A′也在运动，但不变的是点A′是在以B为圆心，以5为半径的圆弧上运动的，这样就很容易想到当A′点落在边BC与⊙B的交点时A′C最小，往从而可求得A′C最小值为3-5。

总之，变中抓不变是一个带有哲学意义的思想方法，它应该贯穿于整个数学教学的过程中，因为利用它，可以使透过现象看到本质，让错综复杂的问题得以破解，从而也让我们的课堂教学更加“数学化”，更加地深入本质，最终让我们学生的数学思维和素养得到根本的提升。

【参考文献】

[1]史宁中.数学基本思想18讲[M].北京：北京师范大学出版社，2016.10：13-14，116-117.

[2]孙维刚.谈全班55%学生怎样考上清华北大[M].北京：北京师范大学出版社，1999.09：143-145.

（作者单位：江山市城南中学）