基于核的k-最近邻在水下目标识别中的应用∗
严良涛 项晓丽
(1 中国人民解放军91388部队 湛江 524022)
(2 广州杰赛科技股份有限公司 广州 510220)
0 引言
水下辐射声场和水声信道的复杂性是造成水下目标识别难度大的根本原因[1]。这两方面因素的影响使声呐接收的噪声信号都是相互耦合、调制甚至畸变的,因此研究者们提出了多种特征提取方法[2−4],试图从不同角度得到噪声信号的特征,但水下环境的复杂性决定了这些特征必然呈现强非线性[5]。在目标识别过程中,为保证识别的正确率应将多种特征加以组合,但这会造成数据维数过高,识别速率下降。为此,本文提出了基于核(Kernel)的k近邻[6](k-nearest neighbor,k-NN)水下目标识别方法。该方法利用主成分分析[7](Principal components analysis,PCA)对高维的特征矩阵进行降维,解决目标识别速率低的问题;利用Kernel技巧将降维后的非线性特征映射到高维空间并在该空间进行k-NN分类识别,能够有效减小非线性特征在低维度空间距离度量误差,提高识别正确率。实际实验数据的验证结果表明:与k-NN相比,基于核的k-NN的目标识别速率略低,但目标的识别正确率得到较大提高;与BP神经网络分类器相比,基于核的k-NN的目标识别正确率略低,但目标的识别速率得到较大提高。
1 基于核的k-NN基本原理
1.1 空间映射及核函数
给定特征样本x,将其从n维特征空间映射到m维特征空间:

其中,S1为原始n维特征空间,S2为m维映射特征空间。x为S1中的特征样本,ψ(x)为对应S2中的特征样本。ψ为将S1映射到S2的非线性映射,φi为特征映射函数,i=1,···,m。
对x,y∈S1,其核函数(Kernel)表示形式为

1.2 k-NN的核化
在k-NN中,原始空间特征样本x和y之间的距离二范数为
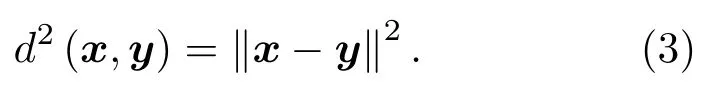
假定将x和y映射至高维特征空间中,那么此时高维空间特征样本ψ(x)和ψ(y)之间的距离二范数为
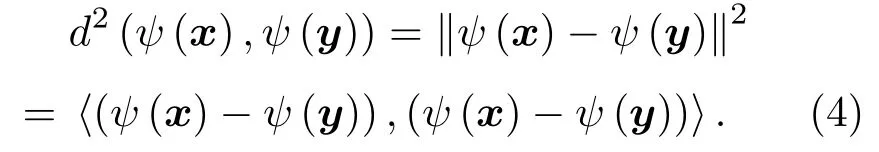
式(4)中存在内积项⟨(ψ(x)−ψ(y)),(ψ(x)−ψ(y))⟩,根据1.1节可知,利用Kernel可实现对该内积的直接计算。此时:
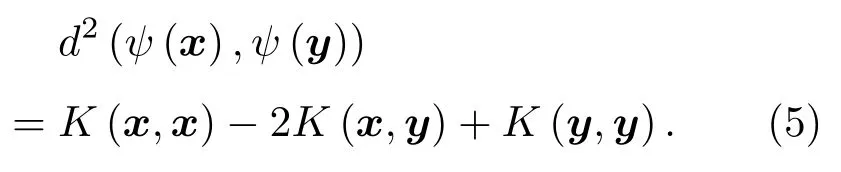
由式(5)可知,高维特征空间样本ψ(x)和ψ(y)之间的距离可通过Kernel在原始空间中直接计算,而不受维度和映射ψ的限制。
1.3 基于核的k-NN的算法实现
基于核的k-NN的实现过程如下:给定一个用于训练的特征数据集,将其映射到高维特征空间,对新的输入实例,利用Kernel计算其在高维特征空间中最邻近的k个实例,若这k个实例的大多数属于某个类,就把该新实例划分为这个类。本文选择高斯核函数进行运算,具体过程如表1所示。

表1 基于核的k-NN的算法实现过程Table 1 The algorithm of k-NN based on Kernel
在上述实现过程中选择的高斯核函数灵活度高,不同的核参数C可以将原始空间映射到任意维空间。在对核参数C的优化过程中,C值过大,高次特征上的权重衰减快,所映射出空间相当于原始空间的子空间;C值过小,可将任意数据映射至线性可分的空间,但这很可能带来严重的过拟合问题[8],因此C值的优化尤其重要。k值的确定采用在一定范围内[9](样本量开平方附近)进行枚举计算确定。
2 基于核的k-NN在水下目标识别中的应用
2.1 数据来源与预处理
将实测的166段水下目标噪声信号进行筛选、标记和梅尔频率倒谱系数(Mel frequency cepstrum coefficient,MFCC)特征提取[10]后,得到120组特征数据,分属4类目标,每类30组,将其中20×4组作为训练样本集D(22×80),其余10×4组作为测试样本集T(22×40)。利用PCA对训练样本集D进行降维,具体过程如表2所示。

表2 PCA的降维过程Table 2 The algorithm of reducing dimensionality with PCA
这样就可以将一个特征样本x映射到一个d′维特征子空间上去,此空间的维度小于原始的d维空间:

本文取阈值t=95%,根据计算确定d′=16,其方差贡献图如图1所示。
从图1可看出,第一主元占方差总和的22%左右,前16个主元占总体方差的95%左右。
训练样本集D(22×80)经过PCA降维后就转换成低维数据集Z(16×80),接下来就可以在矩阵Z中利用1.3节中的基于核的k-NN进行分类。

图1 PCA方差贡献图Fig.1 Variance contribution graph with PCA
2.2 训练过程及分析
选择高斯Kernel进行距离度量计算,不同核参数C值代表将数据集Z(16×80)={z1,z2,···,z80}映射到不同的高维空间。在最优C值的高维空间内同一类别的样本最聚集,正确分类识别率最高。核参数C值的优化属于超参数优化问题[11],本文采用sklearn.grid_search模块下的GridSearchCV对象对C值进行优化,其主要应用对象为小数据集,基本原理是对人工设置的超参数进行网格搜索得到最优值;若算法中存在多个超参数需优化,那么依次选取对模型影响最大的参数调优,直到所有的参数调整完毕。本文中只涉及核参数C值的优化,应用上述方法得到的最优值为45.62。
对k值在样本量开平方附近进行枚举计算确定,得到在训练样本中不同k值与识别正确率之间的关系如图2所示。

图2 k值与识别正确率之间的关系Fig.2 The relationship between k and recognition accuracy
从图2可看出,k=8时识别正确率最高约为88%,实际值为88.23%。
2.3 验证与比较
根据2.1节和2.2节得到的最优d′、C及k值,将测试样本T(22×40)进行分类并与各样本类别标签进行对比得出识别正确率,同时计算每个测试样本识别过程的消耗时间t。与传统线性k-NN和BP神经网络分类器的比较如表3所示。

表3 基于核的k-NN、k-NN和BP神经网络分类器性能比较Table 3 The performance comparison of k-NN based on Kernel,k-NN and BP neural network
由表3可知,基于核的k-NN分类器的平均识别正确率为85%,高于k-NN分类器11.25%,低于BP神经网络分类器2.5%;平均耗时为22.562 s,高于k-NN分类器4.144 s,低于BP神经网络分类器33.908 s。BP神经网络分类器平均识别正确率虽略高于本文基于核的k-NN分类器,但其平均耗时超出基于核的k-NN分类器一倍多;k-NN分类器的平均耗时略小于基于核的k-NN分类器,在可接受范围内,但其平均识别正确率相对于基于核的k-NN分类器过低。所以得出结论:相对于k-NN分类器和BP神经网络分类器,基于核的k-NN分类器综合性能更优。
3 结论
本文利用Kernel技巧将原始空间数据映射至高维特征空间,实现了原始空间的非线性耦合数据在高维特征空间的线性可分,有效解决了水下目标特征数据非线性不可分的问题。并采用PCA对特征数据矩阵进行降维,利用k-NN进行分类识别,形成了基于核的k-NN水下目标识别方法。通过与传统k-NN和BP神经网络分类器对比,说明了基于核的k-NN分类器性能的优越性。

