共形时域有限差分技术在戏场八字墙中的应用∗
黄武琼 卢义刚
(华南理工大学建筑学院 广州 510640)
0 引言
中国传统戏曲是我国乃至世界珍贵的艺术文化遗产,与之相应的演出场所也具有其独特的形式和布局。中国传统戏场主要与宗教活动有关,多建于庙宇之间,从“露台”逐渐变成三面围观的形式,部分戏台还设有八字形侧墙、穹顶等建筑构件。据考察,山西省介休市袄神楼、太原市阳曲县大卜村关帝庙、晋中市榆次城隍庙悬鉴楼等部分戏楼都设有八字墙[1],这类八字形侧墙集中出现在山西省内的戏场中。薛林平等[2]认为,八字墙的设置是古人有意识地改善戏场音质的行为。然而,目前对这一建筑构件的研究还较欠缺,因此本文将利用时域有限差分法(Finite-different time-domain,FDTD)对这类八字墙在戏场中产生的声音效果进行研究。
时域有限差分法最初由Yee[3]提出并应用于解决电磁场问题,随后被应用于其他领域的研究。20世纪90年代,Botteldooren等[4]开始将其引入了声学领域。在电磁场问题中,传统的FDTD方法都是基于Yee直角网格对研究目标进行离散化,对于含有曲面等结构比较复杂的边界采用阶梯近似法。然而,阶梯近似法会带来较大的阶梯近似误差和数值色散误差。为了克服这些缺陷,主要从两个方面解决。其一,减小网格步长。但网格的减小会增大存储内存,增加计算时间。其二,就是采用共形技术。从90年代开始,学者们便提出了多种共形处理方法。1992年,Jurgens等[5]提出了环路法,但这一方法缺乏灵活性,在计算编程时较难实现,并没有得到推广。1997年,Dey等[6]提出了用于电磁场的共形时域有限差分法(Conformal finite-difference time-domain,CFDTD),该方法仅对磁场进行求解,不需要对电场进行处理,结果精度较高而且编程也较容易,但是,CFDTD技术亦存在计算不稳定的问题,当共形网格的面积很小时,需要减小有效网格步长,相应的最大稳定时间步长也需要减小。2000年,Yu等[7]提出一种将变形网格面积近似为规则网格面积的共形技术,虽然精度不如前者,但多用于解决实际的工程问题。2003年,Li等[8]提出简化的共形时域有限差分法(simplified CFDTD,SCFDTD)将面积小于1/6的变形网格近似为规则网格的1/6。2007年,Zagorodnov等[9]提出了有限积分法(Finite integration technique,FIT),不用减小最大的稳定时间步长,运算量和算法逻辑也与阶梯法一样,在现有的FDTD代码中较易实现。之后,学者们主要致力于介电参数和多种方法混合使用方面的研究[10−12]。
建筑声学问题的计算机仿真方法,主要有基于几何声学的声学仿真软件和基于波动声学的有限元法、边界元法、时域有限差分法。时域有限差分法算法比较简单有效,可以直观地反映声波在房间里的传播情况,能够直接得到房间任意点的脉冲响应,从而实现对房间内音质参量的分析。对于戏场中的非直角边界,本文将借鉴电磁场的共形网格CFDTD技术,引进声压更新方程中研究戏场八字墙的声学问题。
1 FDTD共形网格技术
为了便于观察声场变化,本文先考虑二维情形。在理想空气介质中,声波运动方程和连续性方程为

其中,p表示声压;ux和uy分别表示空气质点速度沿着x、y方向的分量;c为空气中的声速;ρ0为空气的静态密度。对于常规均匀直角网格,式(1)∼(3)的中心差分交错格式为

其中,∆t表示离散时间间隔;∆h表示离散空间间隔;n表示离散时间刻度;i和j分别表示在直角坐标系x和y方向的位置。对于曲线边界,需采用共形网格技术。在二维直角坐标系下,曲边经过的共形网格如图1所示,深灰色的区域1为墙体,深灰色以外的区域2为墙体外侧,图中斜线阴影网格为曲边附近的共形网格,需利用共形网格技术来计算。设声压位于直角网格的中心,不管该中心在区域2或区域1。共形网格中,质点速度递推方程与常规网格的递推方程一样,只需处理声压的更新方程[13]。
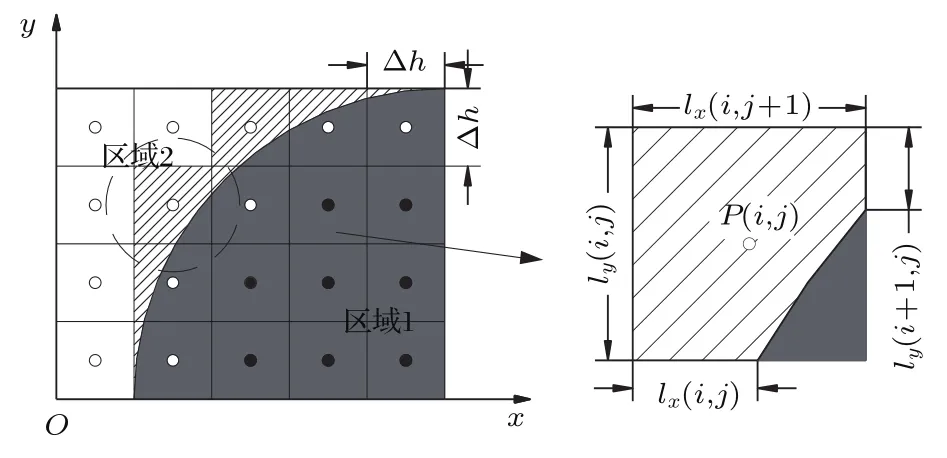
图1 直角坐标系下的共形网格Fig.1 Conformal grids in rectangular coordinates
对式(3)两边进行二重积分,得

由格林公式,式(7)右边可化为

综合式(7)与式(8),可以得到
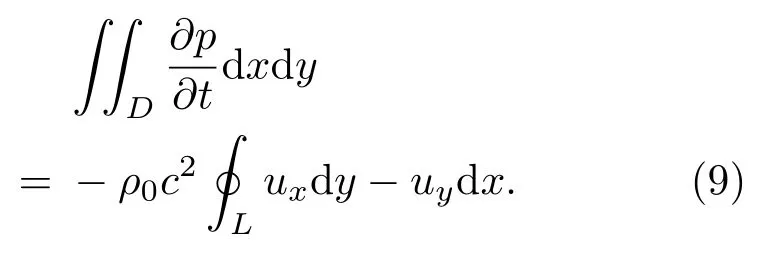
设墙体边界为刚性边界,那么墙体上的质点速度为零,仅需考虑网格中墙体外的质点速度的贡献,于是由式(9)可得共形网格的FDTD递推方程:


其中,lx和ly分别为质点速度对应的棱边在墙体外的长度,A为元胞在墙体外的面积。当lx=ly=∆h,A=∆h2时,式(10)就退化为常规直角网格的递推公式(6),可见,共形网格的更新方程可以用于所有网格的更新方程。为了便于编程,引入相对长度与相对面积

共形网格的更新方程最终化为

共形网格技术的一个关键点在于相对长度和相对面积的求取。若曲线边界是由规则的方程决定,可由方程与网格的交点算出相对长度,以下部分讨论的椭圆房间与八字墙都是规则方程,可以容易计算得到相对长度。共形网格的相对面积一般直接取规则网格面积或者规则网格面积的一半,显然这样处理太粗糙,本文利用双加权平均法求得相对面积[14]。共形网格处理受到变形网格特性的制约,共形面积过小会使程序不稳定,因此,本文利用SCFDTD方法[8],将相对面积小于1/6的网格近似为常规网格面积的1/6,以此来改善计算的稳定性问题。
2 精度验证
为了验证共形网格技术的精确度,模拟一个椭圆房间内的声场变化。根据费马原理,波总是沿着“波程”为极小值的路径传播,从椭圆一焦点发射出的声线,经过界面的各种反射,最终会聚集在另一焦点[15]。以下利用共形网格技术和传统的阶梯法模拟椭圆的曲线边界,比较两者声场结果的精确度。
图2为在6 ms、131 ms、189 ms 3个时刻,3种情况下椭圆房间内的声场分布图。声源采用微分高斯脉冲[16],图2(a)将声源设在偏离焦点水平位置0.7 m处,图2(b)和图2(c)的声源都设在其中一个焦点上。根据稳定性条件,空间步长设为0.07 m,时间步长设为0.117 ms;椭圆形墙壁设为刚性边界。计算的总网格数为180×300。计算用Matlab软件编写。
在6 ms时,波前未到达反射面,波阵面几乎一致,圆形波前向前传播,可以看出利用FDTD方法计算声波方程的精确性和稳定性较好。当声源不设在焦点上时,声线不能在另一焦点聚集,如图2(a)所示;而当声源设在焦点上时,共形网格技术和阶梯法都有聚集焦点的现象,验证了费马原理在声学上的正确性。比较图2(b)与图2(c)可以看出,利用共形网格技术得到的聚焦的声波波前基本上保持圆形波前,而阶梯法得到的聚焦声波波前不够圆。共形技术得到的聚焦区域更集中于焦点,而阶梯法得到的聚焦区域较大,不够集中,共形网格技术比阶梯法的精确度高。
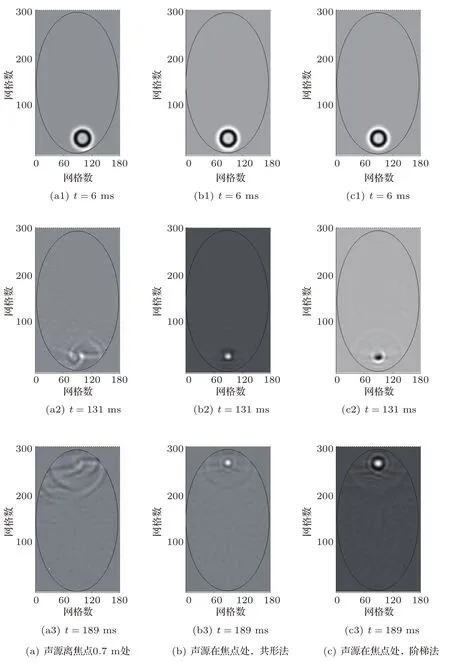
图2 三种情况下椭圆房间内的声场分布Fig.2 Sound field of three cases in the oval room
3 八字墙的声音效果分析

图3 4类戏台平面图Fig.3 Four types of stage plan

图4 设有八字墙戏台的庭院模型Fig.4 A courtyard model of an theater stage with the splayed walls
参考多处戏台的构造,如图3所示,榆次市聂店村戏台的前台在山墙之外,新降县樊店村关帝庙戏台的前台在山墙之间,对于设有八字墙的戏台,太谷县静信寺戏台的八字墙的宽度相对于戏台前台较短,介休市袄神楼戏台的八字墙的宽度相对于戏台前台较长。综合以上戏台的构造和大小,建立大小为23.45 m×23.45 m的含有戏台的庭院模型,如图4所示,戏台两侧设有3.5 m的山墙,紧连着山墙设有八字墙,八字墙的宽度L设为3 m或5 m,八字墙与山墙所在直线之间的夹角θ设为30◦、45◦或者60◦。在戏台中轴线上的5个位置设有声源点,声源采用上述微分高斯脉冲。以中轴线为基准,在庭院内观众席处设两个相邻的测区1和测区2,山墙旁边设测区3。测区1正对山墙之间,测区2紧邻着测区1,面积与测区1相同。山墙与八字墙均设为刚性边界。在实际戏场中,考虑声能消耗,庭院模型四周围合墙壁设为阻抗边界条件[17],平均吸声系数为0.15。
3.1 各个区域的声能分析
为了研究戏台构件的声学作用,考察各个测区获得的声强大小。本文以1 s时长内测区的所有声能叠加作为总声能强度,各个测区内的总声能强度由式(15)计算:

由图5的结果可见,对于无八字墙的戏台,不论声源设在山墙之间或是超过山墙很多距离,在测区1和测区2获得的声能强度都比有八字墙的小。在测区3获得声能强度反而比有八字墙的大。显然八字墙的存在减小了测区3的衍射声能。从图6波阵面可见,声场在山墙顶端产生了次声源,八字墙把衍射声能反射到观众区,无八字墙时,则有较多声能传播到了山墙旁的测区3。当声源距离超过一定位置后,测区2接收到的声强骤减,因此,欲使测区2能接收到较高的声能,声源应尽量在山墙之间,即前台不应凸出山墙太多。
当八字墙的宽度都取5 m或3 m时,如图5和图7所示,声压变化与角度之间没有明显的正比关系,这可能是山墙与八字墙的共同作用导致的混乱现象。当夹角θ为30◦、声源距离在2.8 m时,测区1得到的声强都大于其他两种夹角;但当夹角θ为30◦、八字墙宽为5 m时,在测区2得到的声强较其他两种角度的声强都小。因此,若观众席集中在戏台正前方时,八字墙的夹角设为30◦更佳,若希望观众席的范围扩到两侧更远的地方,八字墙的夹角选择45◦或者60◦更佳,但要综合考虑戏台正前方与两侧都能得到较强的声能,夹角最好取中间值45◦左右。

图6 27 ms时刻两种戏台模型的波形图Fig.6 Waveforms of two stage models in t=27 ms

图7 八字墙角度对声能强度的影响Fig.7 The Influence of the angels of the splayed walls on the sound energy strength
当夹角都为30◦时,除了声源距离为5.95 m时在测区2得到的特殊值外,不管八字墙的宽度为3 m或是5 m,声能强度随声源距离的变化趋势大致相同,如图8所示。当夹角为45◦或是60◦时,声能强度随声源距离的变化趋势也是大致相同的,比较图5与图7即可看出,在此不赘述。取同一夹角时,八字墙的宽度越大,测区1和测区2的声能强度越大,而测区3的声能强度越小,显而易见,八字墙的宽度越大时,观众区接收到的反射声必然会越多,从而也验证了利用FDTD计算声场的正确性。
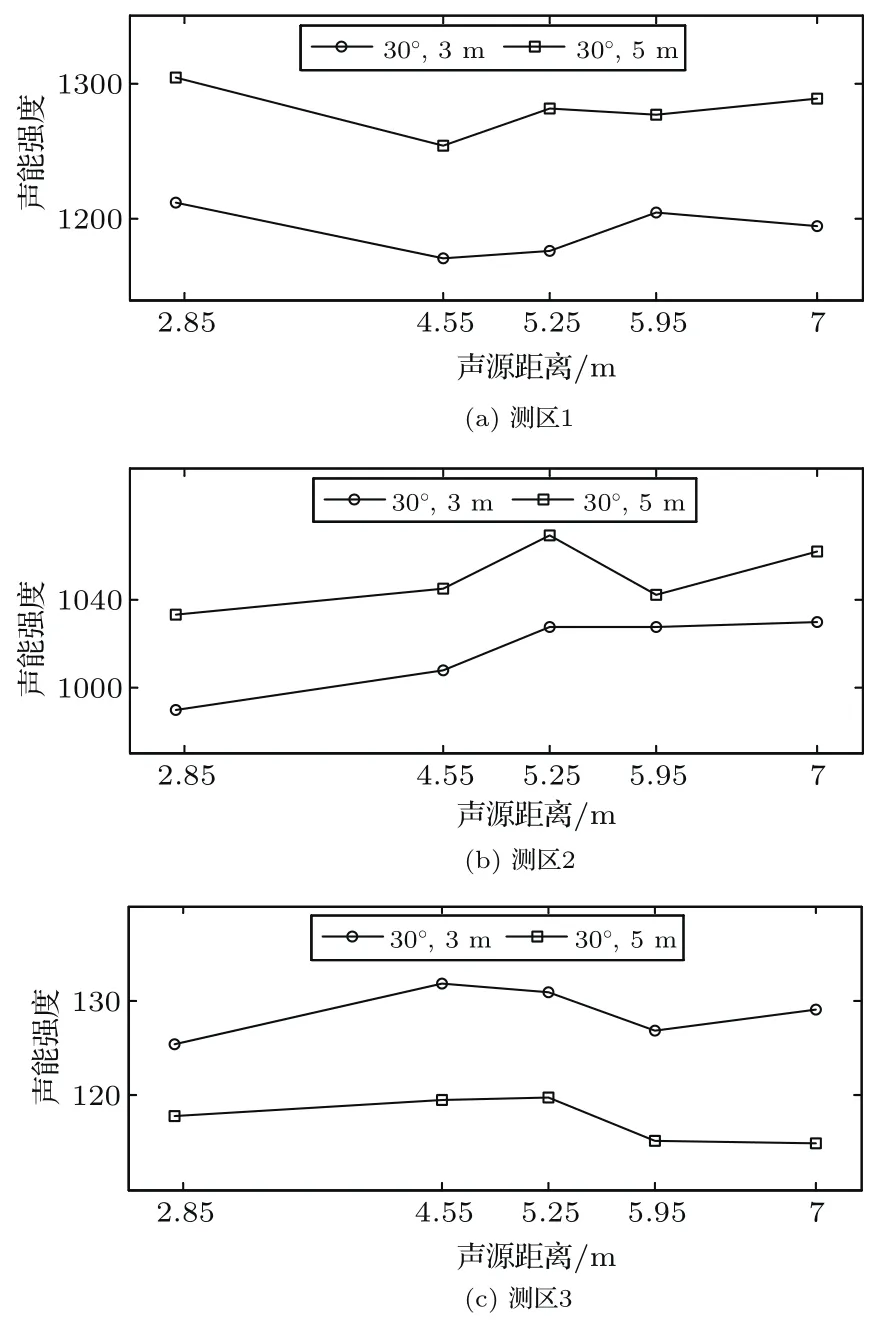
图8 八字墙宽度对声能强度的影响Fig.8 The Influence of the widths of the splayed walls on the sound energy strength
3.2 侧向反射声及早期声分析
20世纪60年代末,声学家们发现了侧向反射声能对于听觉空间感的重要性,据此提出了若干评价指标,较重要的是侧向能量因子(Lateral energy factor,LEF),LEF的定义为
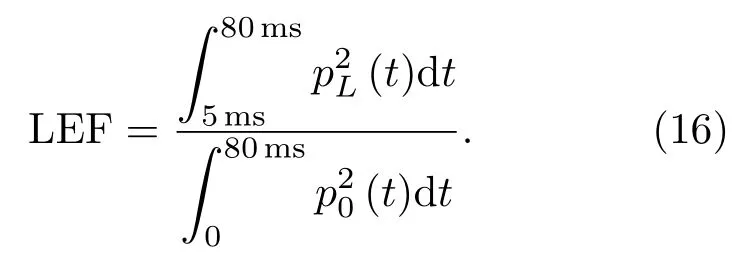
式(16)表示直达声到达后延迟5∼80 ms之内的能量与80 ms之内到达的总能量之比。为了得到八字墙对侧向反射声的作用,将庭院模型中除了后墙的其他三面墙设为完全匹配层(Perfectly matched layer,PML)吸收边界,即忽略侧墙的侧向反射声。在戏台模型的正前方设3个接收点R1、R2、R3,八字墙的正前方另设3个接收点R4、R5、R6,如图4所示,以下只讨论八字墙宽度为5 m时三种夹角的声场情况。经计算,各个模型的侧向能量因子如表1所示。图9是4个模型R1点、R3点和R4点的脉冲响应。

表1 各接收点在4个模型中的侧向能量因子Table 1 Lateral energy factors of receivers in four models
表1的结果显示,有八字墙的侧向能量因子基本都比无八字墙的要大,最大的差值可达0.21,如果LEF值能达到0.2左右或者更大,说明有较丰富的早期侧向反射声,其音乐听感也较好[17]。而且,靠近八字墙正前方接收点的侧向反射声比正对戏台接收点的侧向反射声丰富。从图9中也可以看出,接收点R1的脉冲响应中的反射声没有接收点R3和R4多。此外,60◦夹角时,接收点R4、R5、R6的侧向能量因子明显小于30◦与45◦。从图9(c)亦可见,夹角为60◦时,直达声与后墙第一次反射声之间的脉冲响应与无八字墙的差不多,而夹角为30◦和45◦时在直达声与第一次反射声之间还有一次较强的反射声,此为八字墙提供的早期侧向反射声,比后墙第一次反射声还先到达了接收点。因此,为了使八字墙提供更多的早期侧向反射声,夹角不宜取太大。
此外,从图9各接收点脉冲响应可看出,八字墙对早期声(直达声之后延迟50 ms内到达的反射声)亦有一定的加强作用。表2列出了有八字墙与无八字墙模型的早期声能比,即

其中,p0表示无八字墙时的声压值,p1表示有八字墙时的声压值。由表2中结果可知,夹角取30◦与45◦时,早期声能都大于无八字墙的情况,而夹角取60◦时,接收点R1、R2、R3的早期声能大于无八字墙的情况,接收点R4、R5、R6的早期声能小于无八字墙的情况。可见,八字墙的存在会提供更多的早期声,早期声可以加强直达声,提高声源清晰度,但夹角仍然不宜取太大。
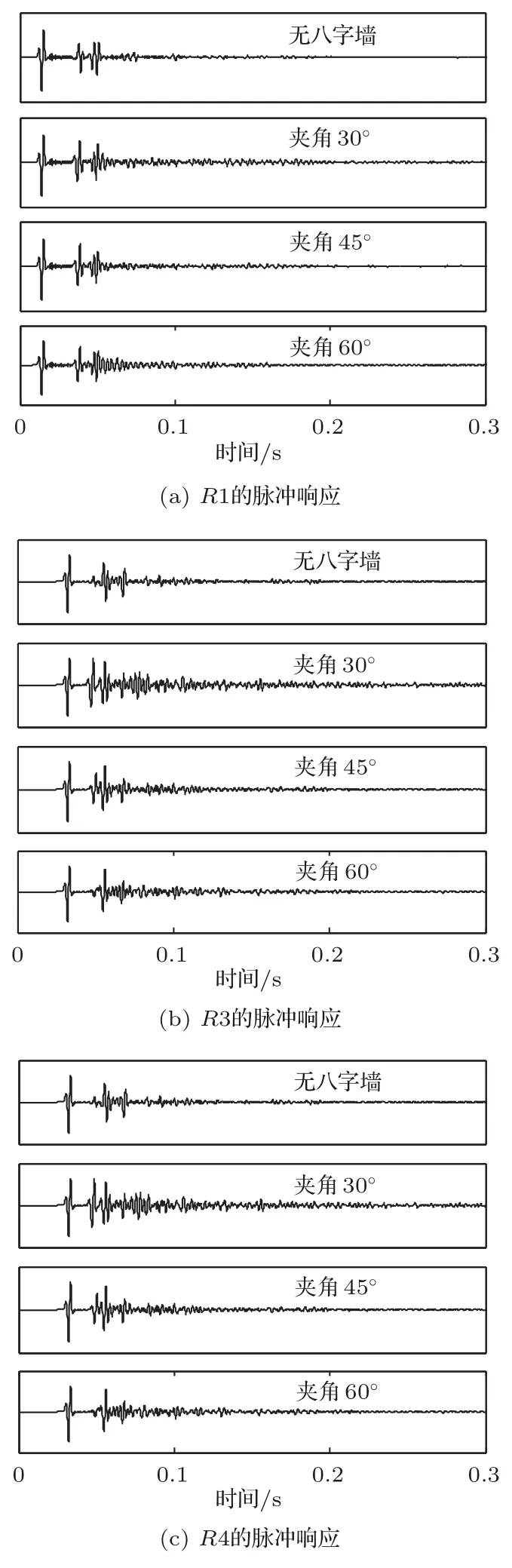
图9 3个接收点在4个模型中的脉冲响应Fig.9 Impulse responses of three receivers in four models
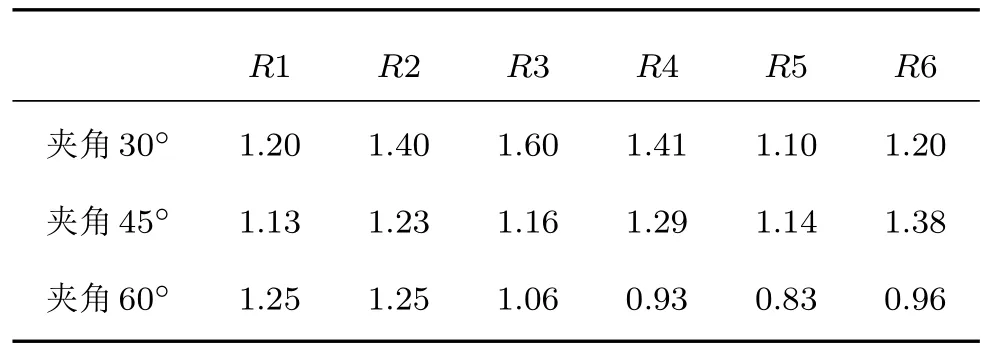
表2 有八字墙与无八字墙模型的早期声能比Table 2 The ratios of early sound energy between models with splayed walls and without splayed walls
4 结论
共形时域有限差分法引入到声波动方程,有利于对曲面边界建筑声学问题计算分析,相比于阶梯近似法具有更高的精确度。共形时域有限差分法分析表明:(1)含有八字墙的戏台比不含八字墙的戏台能加强观众席的声强。(2)八字墙与山墙之间的角度越小,越能加强正面观众席的声音。若将观众席扩充到更大的范围,八字墙的夹角取45◦或60◦时比夹角取30◦时的效果更好,但要综合考虑戏台正前方与两侧都能得到较强的声能,夹角取中间值45◦左右最好。(3)当夹角一定时,八字墙的宽度越长,越能加强观众席的声能大小。(4)八字墙对早期侧向反射声起到一定的加强作用,使听觉空间感更好,但夹角不宜取太大。(5)八字墙可提供更多的早期声,加强直达声的清晰度。
尽管没有确切的八字墙起源的历史记载,古人在戏台设八字墙或许只是主观经验,但从本文计算分析结果看,八字墙对戏台的声场起到了一定的加强作用,在类似的自然声演出场所可参考八字墙构件改善声音效果。

