基于鞍点法与互易性的远探测波场模拟∗
许家旗 胡恒山
(哈尔滨工业大学力学系 哈尔滨 150001)
0 引言
声波远探测技术是近年来发展较快的技术,可以对井外范围数十米的裂缝、断层、地质界面进行探测,具有巨大的应用前景。多年来,国内外对声波远探测方法开展了一系列研究,Hornby[1]在1989年从阵列波数据中提取反射波,并利用偏移的方法得到了井旁地层结构变化的图像。国内薛梅[2]、乔文孝等[3]以及何峰江[4]针对单极源条件下的反射波成像问题展开了一系列研究。但是,单极子声波远探测无法识别反射体的方位,且单极子源较高的声源频率造成其探测范围有限。针对单极子声源存在的不足与问题,Tang[5]首次提出了用偶极子声源来进行声波远探测。随后,Tang等[6]利用四分量偶极数据对井旁裂缝和盐丘内部的精细构造进行了成像。Wei等[7]采用有限差分模拟了偶极源远探测中弹性波的辐射、反射以及接收系数,发现SH波有较大的辐射范围以及较强的接收敏感度,适合反射波成像;在慢速地层中,P波也有较强的接收敏感度,也可用来反射波成像。在声波远探测中,快速准确地进行波场的正演模拟对于成像具有重要的意义。而当井外存在反射体时,结构是非轴对称的,很难获得解析解,通常采用有限差分进行数值模拟[7−9]。在有限差分中,需要设置较小的网格尺寸来模拟井孔,当反射界面距离井孔较远时要耗费大量的时间。为了满足现场测井数据实时处理的需求,快速准确地进行波场计算具有重要的意义。
声波远探测中井孔的存在对弹性波的辐射与接收的影响不可忽略。对于弹性波的辐射,Lee等[10]计算了低频时井内点源激发的远场波场。Gibson[11]计算了声波测井频率范围内井内声源激发的远场波场。对于弹性波的接收,Schoenberg[12]计算了低频时井外入射波在井内激发的波场,Lee[13]研究了井外平面P波、SV波和SH波斜入射时井壁上的位移分布。Lovell等[14]研究了井外平面波以不同角度入射时引起的井内声压。Peng[15]在Schoenberg理论的基础上计算了声波测井频率范围内井外入射波在井内激发的位移与位移场。但是采用Schoenberg理论计算井外入射波激发的井内响应是复杂的,Tang等[16]利用互易性将井外入射波激发的井内响应问题转为井内声源的远场辐射问题,给出了偶极源声波远探测中反射波位移的渐近解可以快速模拟声波远探测问题。Wang等[9]给出了流固分层介质中多极源之间的互易关系,本文将Wang等的互易关系应用在声波远探测中,旨在获得声波远探测中井内波场的渐近解。
本文首先通过鞍点法(也称最速下降积分法)获得井内单极源和偶极源远场辐射场波数域积分的渐近表达式,并将渐近解与实轴积分获得的精确解进行比较,验证渐近解的准确性。井内声源的辐射波遇到界面发生反射,界面反射波可以等效为集中力的辐射波,将反射波激发井内波场问题转换为井外集中力激发井内波场问题。最后,利用井外集中力源与井内声源之间的互易关系获得了反射波场激发的井内响应的渐近解。本文的计算流程如图1所示。
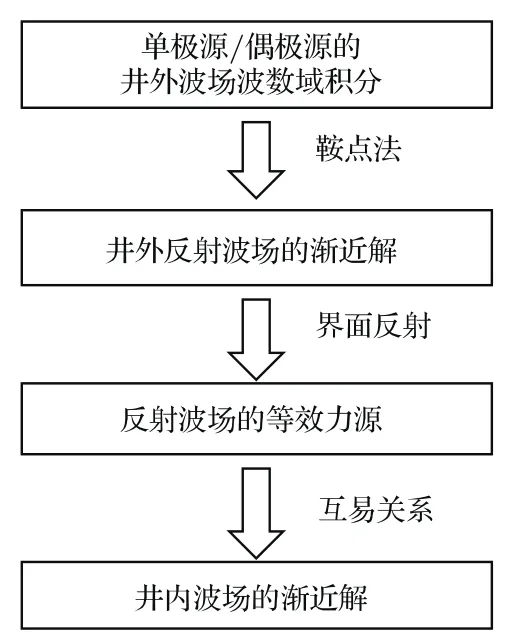
图1 计算流程图Fig.1 Computational flow chart
1 井中声源的辐射场
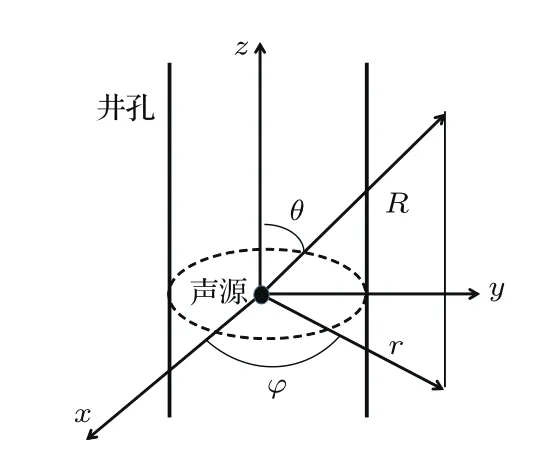
图2 井中声源辐射示意图Fig.2 The model of radiation of the source in the borehole
在本节中首先考虑充液井孔中的井轴处放置单极源或者偶极源,如图2所示,井孔半径为a,R是辐射波传播的距离,φ是方位角,θ是辐射波相对于井轴的倾角。声源用V0G(t)来描述,其中V0是体积变化量,G(t)是声源的时间函数。在本研究里,傅里叶变换表达如下:
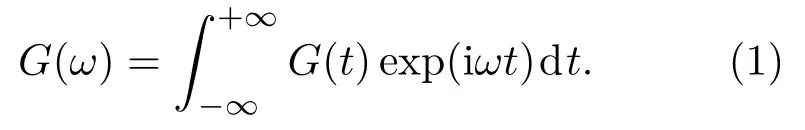
流体中位移可表示为

其中,ϕd是直达波的位移势,ϕr是井内反射波的位移势,∇是柱坐标系下的拉普拉斯算子。
地层中的位移可表示为
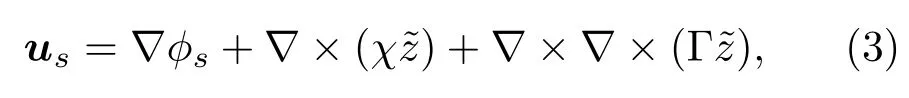
其中,ϕs是地层P波位移势函数,χ是地层SH波位移势函数,Γ是地层SV波位移势函数。
井内的位移势函数可表示为[17]
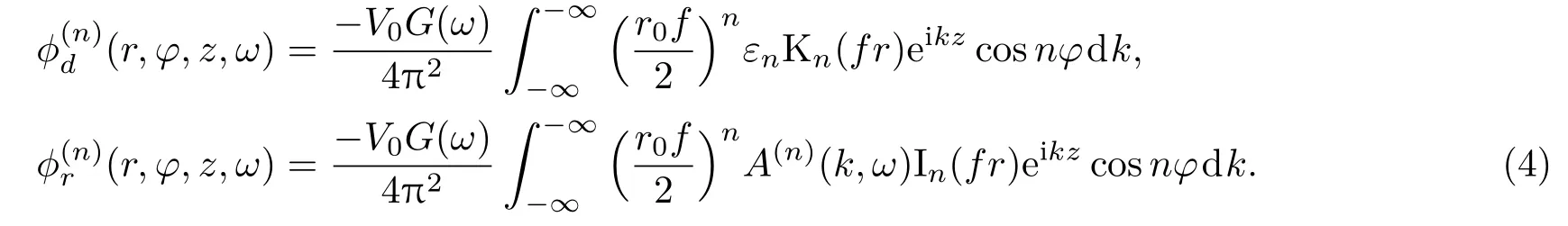
井外的位移势函数可表示为
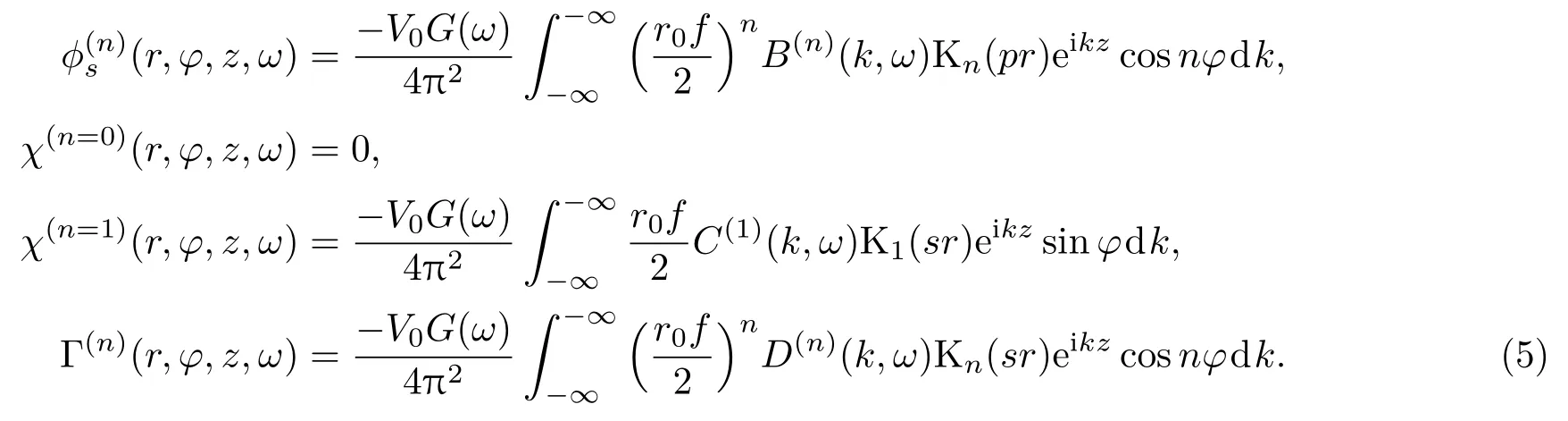
其中,f2=k2−ω2/α2f,p2=k2−ω2/α2,s2=k2− ω2/β2。上标n=0代表单极源,n=1 代表偶极源;In和Kn分别是第一类和第二类贝塞尔函数;εn是纽曼因子,当n=0时εn=1,其余情况εn=2;r0是偶极源的半径;k、f、p和s分别是轴向波数、流体径向波数、纵波径向波数、横波径向波数;αf、α和β分别是流体声速、地层的纵波与横波波速。系数A(n)、B(n)、C(1)和D(n)可以通过井壁上的边界条件来获得[18]。
1.1 最速积分法获得远场辐射场的渐近解
地层中的势函数涉及到复杂的波数域积分,传统的计算方法是采用实轴积分方法进行波数域积分的计算[19],该方法计算较为繁琐。当反射界面离井孔位置较远时,可以采用最速下降积分法获得井孔中声源远场辐射场的渐近表达式[20]:
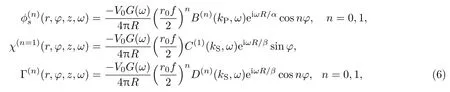
1.2 最速积分法的渐近解与实轴积分法的比较
为了验证远场辐射波的渐近解的准确性,将采用式(6)得到的渐近结果与实轴积分计算的结果进行比较,计算采用的参数由表1给出。地层分别为慢速地层和快速地层2,井孔半径为0.1 m,井外观测点的位置为r=5 m,z=1 m,φ=0◦,声源为中心频率3 kHz、半带宽为2 kHz的余弦包络脉冲函数。图3给出了井外地层为快速地层时渐近解与实轴积分精确解的对比结果,图4给出了井外地层为慢速地层时渐近解与实轴积分精确解的对比结果。从图3和图4中可以看出,无论是慢速地层还是快速地层,采用最速下降积分法得到的渐近结果与实轴积分的精确结果符合较好,这也说明了在远场位置,渐近解是准确可信的,且鞍点的计算与频率无关[6]。
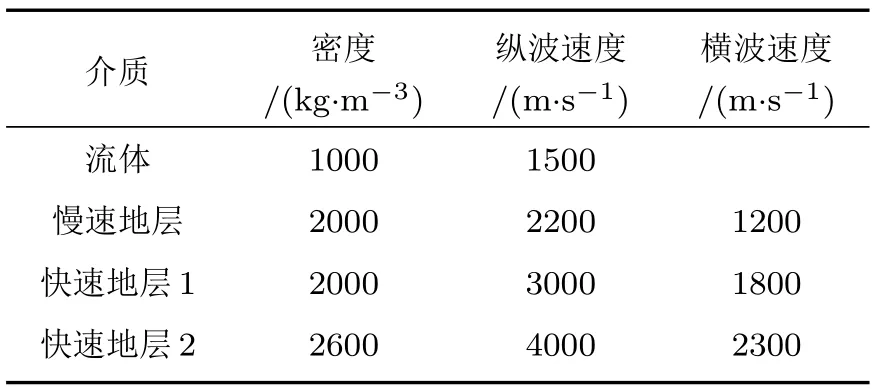
表1 井中流体以及地层参数Table 1 The parameters of the borehole fluid and formations
将式(6)代入式(3),并忽略高阶小项,得到井内单极源的远场辐射位移表达式:
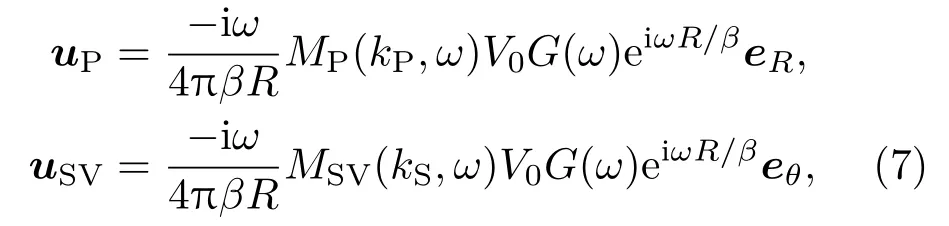
井内偶极源的远场辐射位移表达式为

图3 快速地层条件下采用实轴积分与最速下降积分计算的井外辐射波Fig.3 The radiated wave calculated using real-axis integration and steepest descent integration in the fast formation

图4 慢速地层条件下采用实轴积分与最速下降积分计算的井外辐射波Fig.4 The radiated wave calculated using real-axis integration and steepest descent integration in the slow formation

其中,
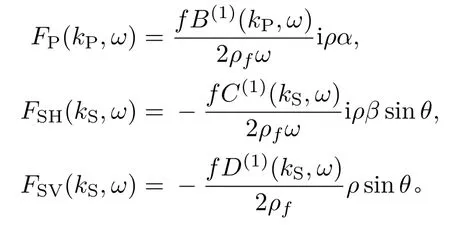
2 反射场的接收
下面研究声源为偶极源时,井内接收到来自井外界面的反射波场。由式(8)可以看出,井内偶极源的远场辐射波具有球面的形式,当遇到界面发生反射。当反射界面的尺寸远大于波长时,可以将界面当成一个无限大平面。当反射界面距离声源较远时,可以将球面波入射可以视为平面波入射,球面波反射系数可以用平面波反射系数代替[20],反射波可以写作

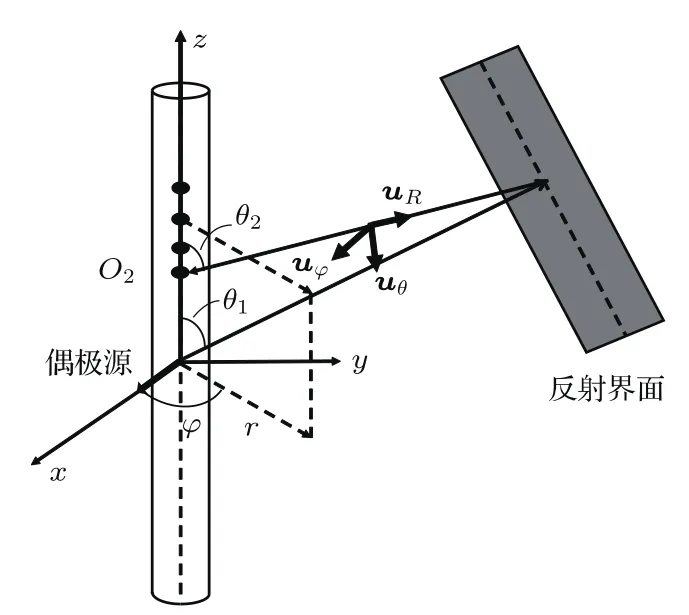
图5 井外存在反射体时的反射波示意图Fig.5 The reflected wave from the reflector outside the borehole
其中,GSH、GSV和GP分别是SH波、SV波和P波的反射系数。反射波uφ、uθ和uR的偏振方向如图5所示。
从界面反射回来的波由井中的接收器接收,在远探测的声波频率范围内,井孔的存在对波场的影响不可忽略。采用Schoenberg理论[12]计算井内的波场比较复杂,在本文中,在已知井内辐射场的基础上,利用互易定理求解反射波在井内激发的位移以及声压。
2.1 反射波场的等效虚源
无限大均匀弹性介质中,集中力在该力的作用线上的位置激发且只激发出球面纵波[21],
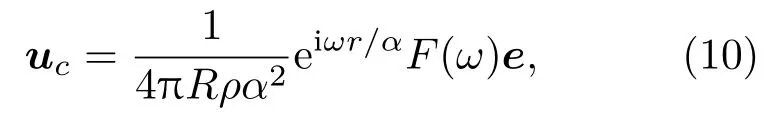
其中,F(ω)为集中力的大小,e为集中力的方向,是观测位置与集中力之间的距离。在垂直于该力方向并经过其作用点的直线上集中力激发且只激发出球面横波us,
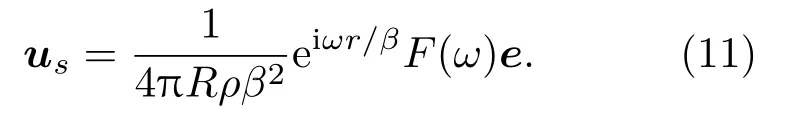
将反射波式(9)代入式(10)和式(11),可以得到与反射波等效的集中力源:
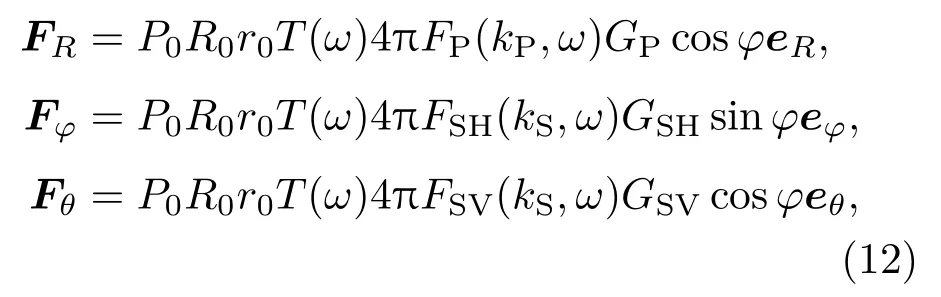
式(12)中,P0R0表示在距离声源R0的压强为P0,T(ω)为声压源的频谱函数[22]。如图6所示,等效集中力FR、Fφ和Fθ作用的位置与声源关于反射界面对称,其中FR沿反射P波的偏振方向,Fφ沿反射SH波的偏振方向,Fθ沿反射SV波的偏振方向。这样就将求解反射波激发的井内响应问题转化为求解井外虚源激发井内响应问题,虚源由三个相互正交的集中力构成。注意到在图6中,在反射波等效为虚源的辐射波后,反射界面也不再存在了。
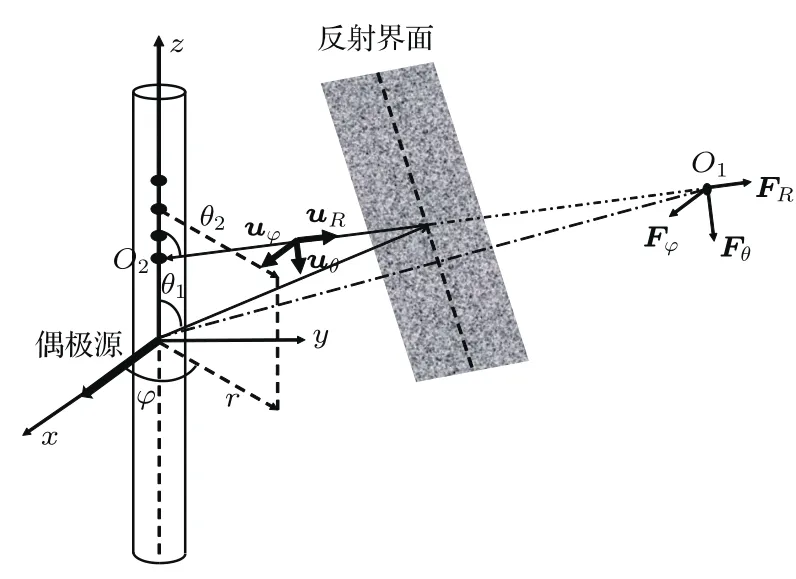
图6 反射波的等效集中力Fig.6 The concentrated force equivalent to the reflected wave
2.2 利用互易性获得井中反射波场的响应
为了获得井外集中力激发的井内响应,利用互易定理求解。Wang等[9]建立了多极声源以及集中力源在流固分层介质中的互易关系。首先求井外集中力激发的井内声压,如图7所示。
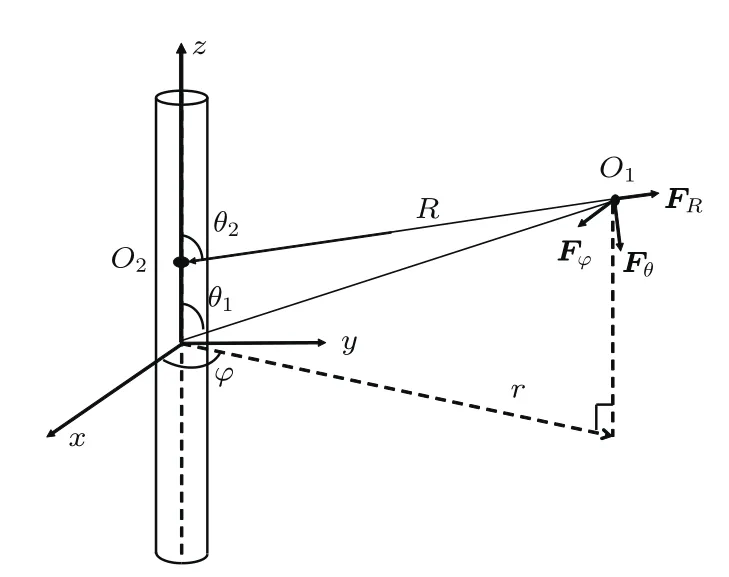
图7 井中接收声压信号示意图Fig.7 The reception of pressure in the borehole
为了获得井中O2处的声压,在O2处放置一个单极源膨胀点源,其在井外远场O1处的辐射位移ui(i=R,θ,φ)由式(7)给出。单极源与集中力之间的互易关系为[9]
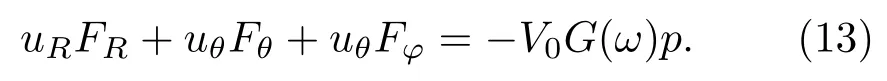
将式(7)和式(12)代入式(13),得到反射波激发的井内声压p,

其中,

L是波传播的总距离,θ1是辐射波传播方向相对于井轴的倾角,θ2是反射波传播方向相对于井轴的倾角。
类似地,如图8所示,为获得井外集中力激发的沿x方向井内位移,在接收位置O2处放置一个沿x方向的偶极源D,其在井外O1处的辐射位移ui(i=R,θ,φ)由式(8)给出。单极源与集中力之间的互易关系为[9]
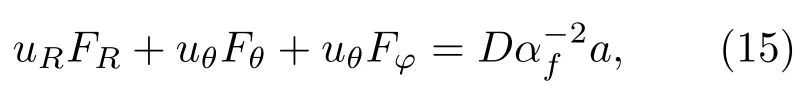
其中,a=−ω2u′是O2处沿x方向的加速度。将式(8)和式(12)代入式(15),获得反射波激发的井内沿x方向井内位移,
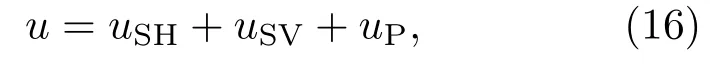
其中,
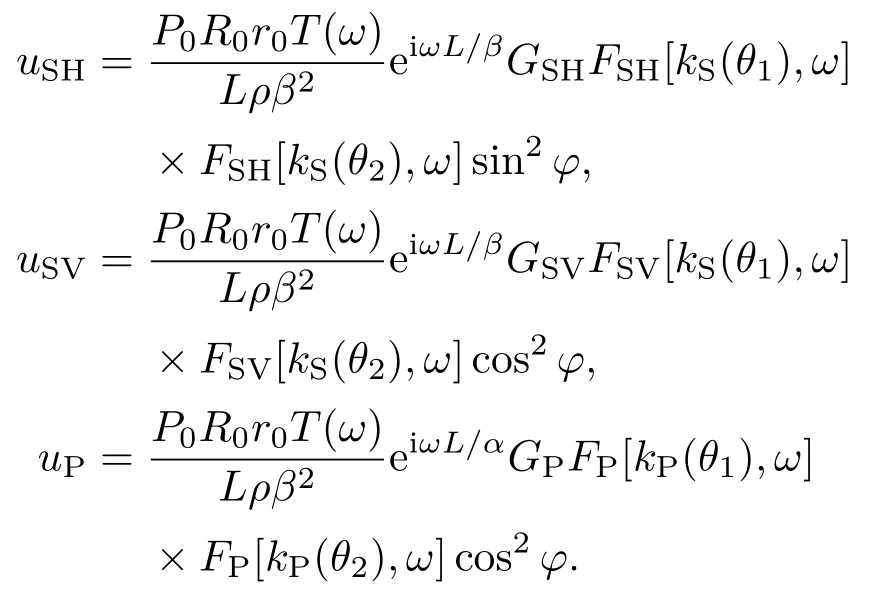
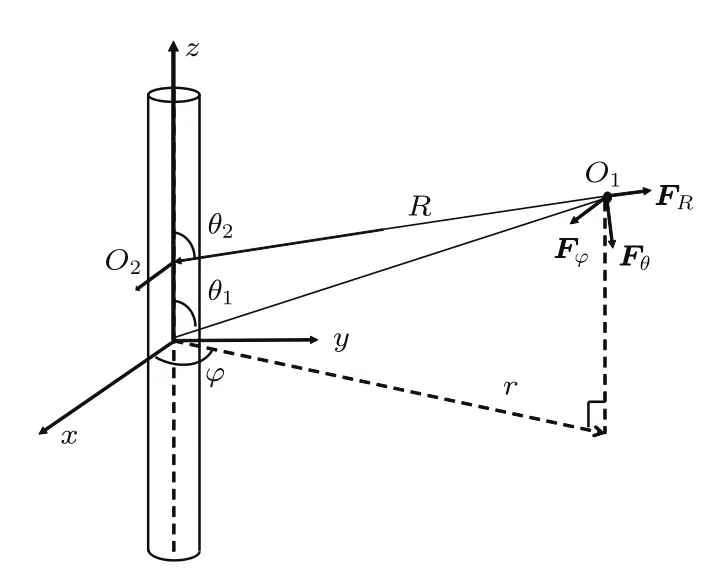
图8 井中接收位移信号示意图Fig.8 The reception of displacement in the borehole
为了验证渐近解的准确性,采用三维有限差分模拟声波远探测中反射波激发的声压与位移,如图9所示,反射体距离声源3 m,倾角为15◦,计算参数在表1给出,声源的中心频率为3 kHz,声源为偶极源并可以沿井轴旋转。
当偶极源方向平行于反射界面,接收沿x方向的位移,采用渐近解与数值解的对比结果如图10所示。从图10中可以看出,渐近解模拟的反射SH波与有限差分吻合较好,当偶极源方向平行于反射体走向时,只有SH波的位移且SH波位移达到最大,除此之外,全波中最先达到的是弯曲波,幅度在全波中最大。
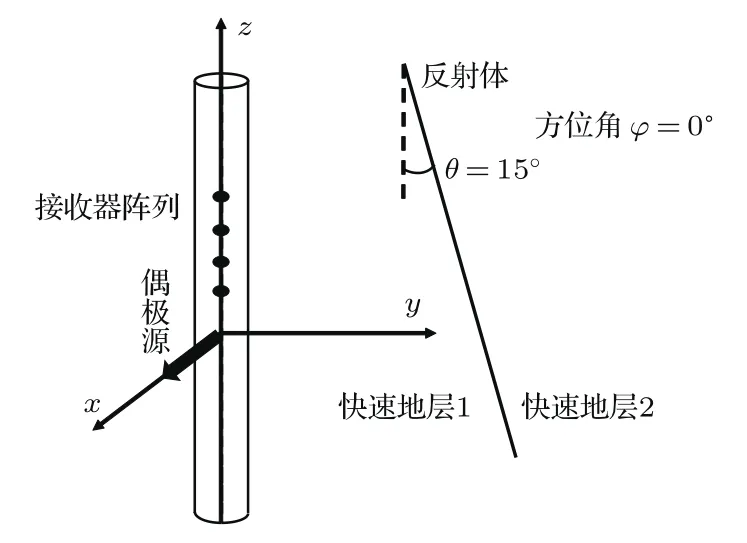
图9 偶极声波远探测示意图Fig.9 The model of dipole single-well imaging
当偶极源方向指向反射界面,接收声压,采用渐近解与数值解的对比结果如图11所示。从图11中可以看出,渐近解与数值解的结果吻合较好。渐近解与数值解之间的差异来自于P-SV转换的贡献,随着收发距离的增大,转换波的贡献随之增大,这是因为收发距离增大时入射角也变大,导致反射波的P-SV转换系数增大。显然,当反射界面距离声源较远时,入射角变小,转换波减小,渐近解与数值解之间的误差也会变小。值得注意的是,当采用偶极声源发射,单极接收的收发方式,接收的全波中没有井孔弯曲波,这也是与Kurkjian等[17]的结论是一致的。这种混合模式的收发方式,理论上可以达到消除井孔波而凸显出反射波信号的目的,这将有利于后续的信号提取以及反演。另外,从式(14)可以看出,当反射体方位角改变180◦时,接收的声压信号的极性发生偏转。目前远探测中存在的反射体方位角180◦不确定性问题[5−6],而本文的研究发现:采用偶极发射-单极接收的收发模式,当方位角改变180◦时,接收的信号极性发生偏转,这可以用来消除反射体方位角不确定性来唯一确定反射体方位角。

图10 井内位移渐近解与数值解之间的对比Fig.10 Comparison between asymptotic solutions to horizontal displacement at the borehole axis and exact numerical results to displacement
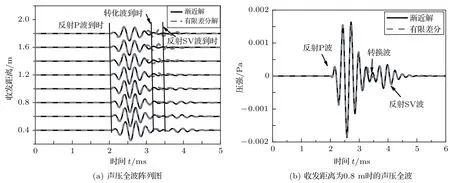
图11 井内声压渐近解与数值解之间的对比Fig.11 Comparison between asymptotic solutions to pressure at the borehole axis and exact numerical results to pressure
通过与有限差分结果的比较,验证了渐近解的正确性。而采用有限差分要耗费大量的时间,同时对计算机的性能要求很高,而采用渐近解可以快速获得波场的正确结果,对于实际声波远探测中数据实时处理具有重要的意义。
3 结论
本文采用解析法给出了求解声波远探测中非轴对称波场的具体方法,获得了以下结论和成果:
(1)采用鞍点法计算了充液井孔中偶极源和单极源激发的远场辐射波场的渐近解,并与采用实轴积分法计算的精确结果相一致,证明了采用鞍点法计算井外辐射场的准确性。
(2)当井外存在倾向的反射界面时,来自界面的反射波可以等效为三个集中力源的辐射波,利用井内单极源与井外集中力之间的互易关系获得了井内声压信号,利用井内偶极源与井外集中力之间的互易关系获得了井内位移信号。此解析法计算结果与有限差分的结果一致,且解析法显著提高了计算效率,对于实际测井中数据的实时处理具有重要意义。
(3)传统的声波远探测仪器采用同一类型的声源与接收器,例如声源和接收器都为单极或者偶极,这种收发模式接收到的波场信号中含有较强的井孔模式波且幅度较大,不利于反射波的提取。采用偶极源发射,居中单极接收的收发模式,理论上可以消除井孔模式波来凸显反射波,可提高实际测井数据实时处理的效率。
(4)在偶极发射-单极接收的收发模式下,当反射体方位角改变180◦时,接收的反射波波形极性会发生偏转,可以用来消除目前声波远探测中反射体方位角多解性问题来唯一确定反射体方位角。
——超集中力
—— 梁在集中力作用点处的剪力分析

