平板扬声器立体声重放的振动对比度控制方法∗

李子庆 罗平展 李晓东

(1中国科学院声学研究所 北京 100190)

(2中国科学院大学 北京 100049)

0 引言

平板扬声器通过激励薄板产生弯曲波向周围空气辐射声能量。典型的平板扬声器由一块矩形薄板和固定在薄板上的力激振器组成，激振器激励薄板产生弯曲波振动辐射声波。平板扬声器轻薄，工作频带宽，高频辐射没有明显的指向性，辐射声场可近似为扩散型[1−2]。此外，辐射声场存在较大失真，相关研究对该类型扬声器进行了优化设计获得了平坦的响应曲线[3−5]。

多媒体设备的显示屏也可以作为平板扬声器的振动结构辐射声波[6]。这种发声方式一方面可以使设备更加轻薄，另一方面显示屏局部振动辐射的声场可以再现声源的空间信息，进而增加一定的沉浸效果。利用加筋的方法可以将OLED显示屏划分为左中右三个相互隔离的振动区域，每个区域有对应的激振器激励该区域的屏幕振动。该方法将左声道、中置声道和右声道信号分别馈给对应区域的激振器从而实现了多声道声重放[7]。除上述改变结构的方法，利用阵列信号处理技术也可以在平板的不同区域重放不同的声源信号，而相关的研究比较少。Heilemann等[8]利用模态叠加方法(Eigenfunction superposition,ES)在一定频带范围内实现了声源的局域化，并利用该局域化控制方法在一个铝板上实现了多声源重放。该方法一方面需要获得模态的先验信息；另一方面为了保证模态的独立可控性，激振器的数量需要等于独立可控模态的数量。独立可控的最高阶模态固有频率决定了有效带宽的上限，即激振器的数目越多有效频带越宽。在触觉反馈应用中，Woo等[9]利用模态叠加(ES)和行波控制(Traveling wave control,TWC)两种方法在300 Hz单频处也实现了振动的局域化控制。

本文利用激振器阵列通过振动对比度控制方法(Vibrational contrast control,VCC)在平板上实现声源的局域化控制，并利用该控制方法实现平板扬声器的立体声重放。首先针对某一声道信号，将平板的对应区域定义为辐射区，其他区域为非辐射区。通过最大化辐射区的平均动能将该声道声源集中在辐射区。辐射区内平板振幅较大，辐射声功率较强，而非辐射区振幅较小，辐射声功率较弱。然后通过弯曲波振动的线性叠加使左右声道的声源分别位于平板的左侧和右侧。最后通过实验表明该方法可以在较宽频带范围内实现声源的局域化，从而可以在平板扬声器上实现立体声重放。

1 理论背景

1.1 各向同性有限平板的振动方程

位于xOy平面的平板沿z轴方向的弯曲波振动方程为[10]

其中，f(x,y,t)为平板在z方向受到的外力，ρ为平板密度，h为平板厚度，D为弯曲刚度，

其中，E为杨氏模量，ν为泊松系数。假设阻尼比为η，此时弯曲刚度D′=D(1+jη)。

结构的振动响应可以表示为系统固有模态的线性组合。理想情况下，完备的结构模态空间由无穷个相互正交的模态组成。模态的固有频率距离工作频率越远，该模态对结构振动的响应贡献越小。对于有限的工作带宽，一般仅保留对结构响应贡献较大的前R阶模态。假设各激振器位置为(xn,yn),n=1,···,N，其产生沿z轴方向的点源力。省略时间项ejωt，平板在z方向的复位移幅度为(x,y)，其在(xn,yn)处受到的简谐力幅度为(xn,yn)。(x,y)可以分解为R个振动模态的叠加，

将各模态按照固有频率从小到大的顺序排序，r表示排序后各模态的阶数，r1和r2分别表示第r阶模态在x和y方向的模态序数。Mr、ωr、ϕr(x,y)和分别为第r阶模态的模态质量、固有频率、固有振型和激励简谐力幅值

平板在z轴方向的振动速度为位移(x,y)ejωt对时间的导数，

其中Hr为第r阶模态的频率响应，

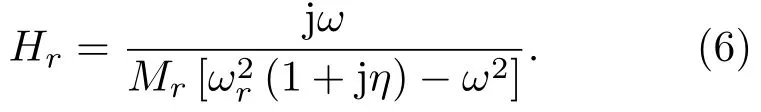
在实际应用中，平板多用矩形框固定，其边界条件可近似为固支边界。在固支边界条件下，各模态的固有频率和固有振型计算复杂。相关研究证明，固支边界条件时固有频率可以近似为修改模态序数r1=r1+∆r1和r2=r2+∆r2后的简支边界条件下的固有频率，其中∆r1和∆r2称为“边界效应因子”；固有振型可以直接近似为简支条件的振型[11]。

其中，固有振型向量Φ=(ϕ1,ϕ2,···,ϕR)，激振器的输出向量f=(f1,f2,···,fN)T，模态的频率响应矩阵H=diag(H1,H2,···,HR)，激振器阵列输出和模态力的耦合矩阵为

令Y=ΦHΦc为激振器阵列到平板上一点的导纳函数，其中第n列表示第n个激振器在平板上产生的速度场，公式(7)可以表示为

本文通过传感器进行测量得到导纳函数Y；利用该函数，通过振动对比度控制方法实现平板扬声器的声源局域化控制。该方法不需要预先估计平板各阶模态的固有频率和固有振型。

1.2 振动对比度控制

利用激振器阵列将平板的振动能量局域在某一个子区域，该子区域内平板振速较高，辐射声场的能力强，称为辐射区；其他区域振速较低，辐射声场的能力弱，称为非辐射区。相似的算法被用于扬声器阵列的局部声重放应用中[12−15]，例如声能量对比度控制。局部声重放技术将声音内容传播到听音者所在的听音区域，同时抑制声音在同一空间中其他区域的传播。设输入信号，激振器阵列的空间滤波器为q，则各激振器的激励信号f=。定义整个平板的振动区域为振动区，用符号Ωt表示。将振动区分为辐射区Ωr和非辐射区Ωm，其中Ωt=Ωr∪Ωm且Ωr∩Ωm=∅(∅表示空集)。各区域振动总动能为

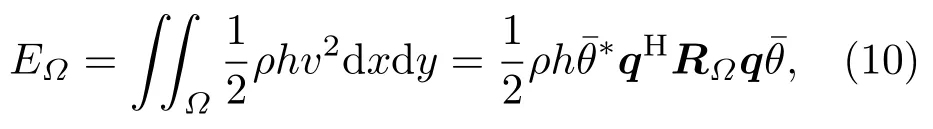
其中Ω∈{Ωt,Ωr,Ωm}，各区域对应的空间相关矩阵RΩ为

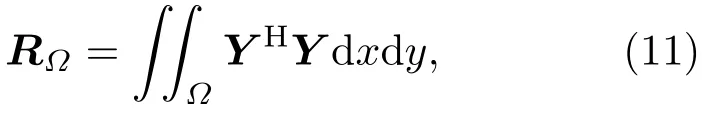
[RΩ]ij表示第i和j个激振器产生的振动场在区域Ω内的空间相关性。设平均动能比值

其中，Sr为辐射区面积，St为振动区面积。当空间相关性矩阵RΩt可逆时，C表示辐射区Ωr和振动区Ωt的平均动能之比。最大化公式(12)的最优空间滤波器qo为

即最优空间滤波器qo为矩阵的最大特征值Cmax对应的特征向量。

平板的总动能等于辐射区动能和非辐射区动能之和。令非辐射区和振动区的平均动能之比为C′，

其中，Sm为非辐射区面积。则C和C′满足如下关系式：

由公式(15)可知，最大化辐射区和振动区的平均动能比值C等于最小化C′，因此最大化C可以间接实现最大化辐射区和非辐射区的平均动能比值。

VCC方法旨在最大化辐射区动能和平板总动能的比值。当约束辐射区的平均动能大于某一固定值Er时，最优滤波器qo需要乘以适当的系数以满足辐射区约束条件。当空间相关性矩阵不可逆时，即至少两个激振器产生相同的振动场，VCC方法会抑制平板的总动能而并非最大化辐射区动能。由于在低频段模态叠加因子(Model overlap factor,MO)较小，所以各激振器产生的速度场相关性较高。虽然VCC获得了较大的动能比值，但是此时平板的总动能较小，即局域化控制方法增加了平板的等效机械阻抗。通过正则化技术可以在最大化平均动能比值和减小等效阻抗之间取折衷。此时最优空间滤波器为

其中，λ为正则化参数，Q{∗}表示求矩阵∗最大特征值对应的特征向量。

λ取值较大时平板的动能较高，辐射区和振动区的平均动能比值较小，在非辐射区也存在较强的声源；λ取值较小时可以获得较大的平均动能比值，但是此时平板的等效机械阻抗较高，辐射功率较小。由公式(5)可知，激振器产生的速度场为各阶模态振速的叠加，频率越高，MO越大，各激振器产生的速度场相关性越小。因此频率较低时λ取值较大，频率较高时λ的取值较小。

由于弯曲振动在z方向的位移幅度远小于板厚度，所以利用叠加定理可以使平板的左右区域分别播放立体声的左右声道信号。假设左右声道信号分别为θL和θR。以左侧区域为辐射区，其他区域为非辐射区的最优滤波器为qoL；以右侧区域为辐射区，其他区域为非辐射区的最优滤波器为qoR。左右声道信号分别由对应滤波器滤波后相加，然后馈给各激振器激励平板振动。叠加后的激励信号为

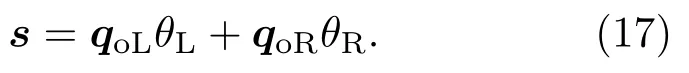
利用公式(17)计算的激励信号激励平板振动，可以在平板的左右辐射区辐射对应声道信号，实现左右声道声源的空间解耦。

2 平板局域化振动控制分析

为了验证控制方法的有效性进行仿真分析。仿真的平板长度la、宽度lb和厚度h分别为0.480 m、0.270 m和0.001 m。仿真模拟平板为铝制薄板的情况，故杨氏模量、密度和泊松比分别取68 GPa、2700 kg/m3和0.33。边界条件为固支边界，阻尼比η取0.01[16]。仿真利用模态叠加方法计算激振器阵列到测量点的导纳函数，其中模态序数r1和r2的最大值分别取16和10，共160个模态，且第160阶模态的固有频率约为6000 Hz。

2.1 单声道振动控制

各区域划分如图1所示，其中辐射区的中心位置为(0.85la,0.50lb)，长宽分别为0.30la和1.00lb。在x和y方向的采样点数分别为16和10。当平板阻尼较大时，高频段平板仅在激振器附近区域振动。因此为兼顾高频播放，在平板的左右两区域分别布置4个激振器，以平板左下角为坐标原点，各激振器坐标如表1所示。

图1 辐射区测量点、非辐射区测量点和激振器位置Fig.1 The locations of the actuators and the measurement points for the radiated zone and the non-radiated zone

表1 激振器阵列坐标Table 1 The coordinates of the actuators

图2为λ取不同数值时平均动能比值和振动区总动能随频率的变化，其中λ0=0表示不进行正则化处理，λ1、λ2和λ3分别为0.001、0.01和0.1。一方面λ取值越小，平均动能比值越大，平板的总动能越小。另一方面激振器产生的速度场相关性越高，平板的总动能越小。因此VCC增加了平板的等效机械阻抗。例如图2(b)中λ为0或0.001时，频率较低时MO较小，激振器产生的速度场相关性较高，VCC方法控制后平板的等效机械阻抗较大，总动能较小。频率较高时由于阵列可以有效激励的模态数量不同，导致不同频率处MO不同，MO较大的频段速度场相关性较低，平板的总动能较大；相反MO较小的频段速度场相关性较大，总动能较小。

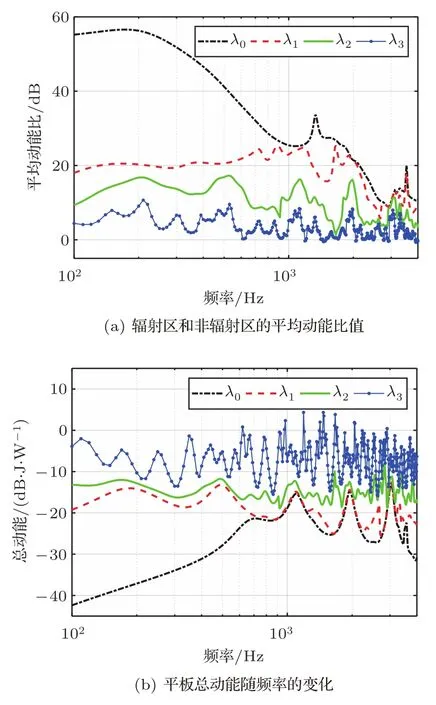
图2 λ取不同值时，平均动能比值以及平板总动能随频率的变化Fig.2 The average kinetic energy contrasts and the total kinetic energies of the flat panel plotted as a function of frequency with different value ofλ

相关的局域化控制方法主要有ES和TWC。ES首先将目标振动形状展开为模态叠加形式，并将其截断为前几阶模态的叠加。然后通过激振器阵列控制这些模态的幅值和相位，利用这些模态的叠加在一定频带内实现目标振型。TWC首先求出激振器阵列到测量点的导纳函数，然后利用最小二乘法获得实现目标振型的最优空间滤波器，最后输入信号通过该滤波器滤波后馈给激振器阵列激励平板按照目标振型振动。结合本文VCC方法，对不同的局域化控制方法进行比较，其结果如图3所示。其中VCC和TWC在100 Hz∼4000 Hz利用按照表1分布的激振器阵列进行辐射区局域化振动控制，且正则化参数λ=0.0025；ES利用前8阶模态实现局域化控制，由于第8阶模态的固有频率约为350 Hz，所以该方法的有效频带范围为20 Hz∼350 Hz。针对ES方法，仿真中利用低通和高通滤波器将输入信号分为低频和高频两部分，其中低通和高通滤波器均为6阶Butterworth滤波器，3 dB截止频率分别为400 Hz和800 Hz。低频部分，为保证模态的独立可控，需要对激振器的位置进行优化。本文利用文献[8]中的优化结果布置激振器阵列的位置，对低频部分进行局域化控制。高频部分，基于平板仅在激振器附近产生振动的假设[8]，采用额外的一个激振器播放高频信号，该激振器放置于辐射区的中心位置处。此外图3也给出了不进行局域化控制，利用同一个输入信号同时驱动8个激振器激励平板产生振动的结果。

图3 平均动能比值以及平板总动能随频率的变化Fig.3 The average kinetic energy contrasts and the total kinetic energies of the flat panel

如图3(a)，三种方法在各自的有效带宽范围内均可以实现较好的局域化控制效果，频率较高时由于激振器数量限制使VCC和TWC的局域化效果有所下降。在100 Hz∼4000 Hz范围内，VCC的平均动能比值均不低于TWC。采用8个激振器时，ES理论上在350 Hz以下均有较好的局域化效果，其仿真结果和理论相符合。ES在400 Hz以上频段不进行局域化控制，由于阻尼比η较小，即使在较高频段用于播放高频信号的激振器产生的振动也分布于整个平板，所以ES在较高频段没有局域化效果。图3中黑色虚线为不进行局域化控制的结果，此时平板没有局域化效果，辐射区和非辐射区的平均动能比值约为0 dB。此外在一些频率处，平均动能比值出现“谷点”，例如120 Hz、450 Hz、1050 Hz等，这是因为平板在这些频率处模态的线性叠加使非辐射区出现较大振动。例如120 Hz时平板的振动形式主要有(1,1)和(1,3)模态决定，两模态的叠加使平板的辐射区振动较弱而非辐射区振动较强。图3(b)为平板的总动能随频率的变化。三种控制方法均使平板的动能减小，即平板的等效机械阻抗增大。和另外两种方法相比，ES在有效控制带宽内平板的动能更低。

图4为最优化空间滤波器的频响曲线，其中位于辐射区一侧的滤波器具有较高的幅度响应，而位于非辐射区一侧的滤波器幅度响应相对较低，例如在低频段激振器A5∼A8高于A1∼A4约20 dB。当λ=0.0025时，辐射区和非辐射区的平均动能比值以及振动区总动能如图5所示。其中平均动能比值随频率变化，在2000 Hz以下平均动能比值约为17 dB；2000 Hz以上频段由于激振器的数目限制，控制效果下降并且波动较大，平均动能比的平均值约为6 dB。图5(b)为各区域总动能随频率的变化。三条曲线的峰谷位置相同，其中“谷点”表明该频率时各激振器产生的速度场相关性较强，局域化控制算法使平板的动能减小，等效机械阻抗增大。

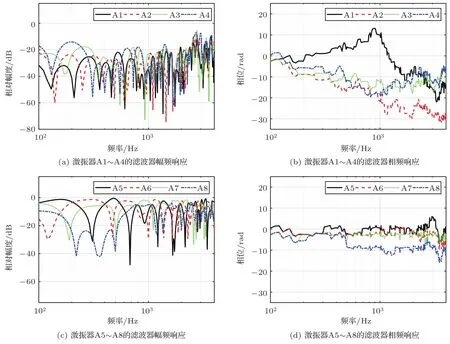
图4 最优滤波器的频响曲线Fig.4 Frequency responses of the optimal filters

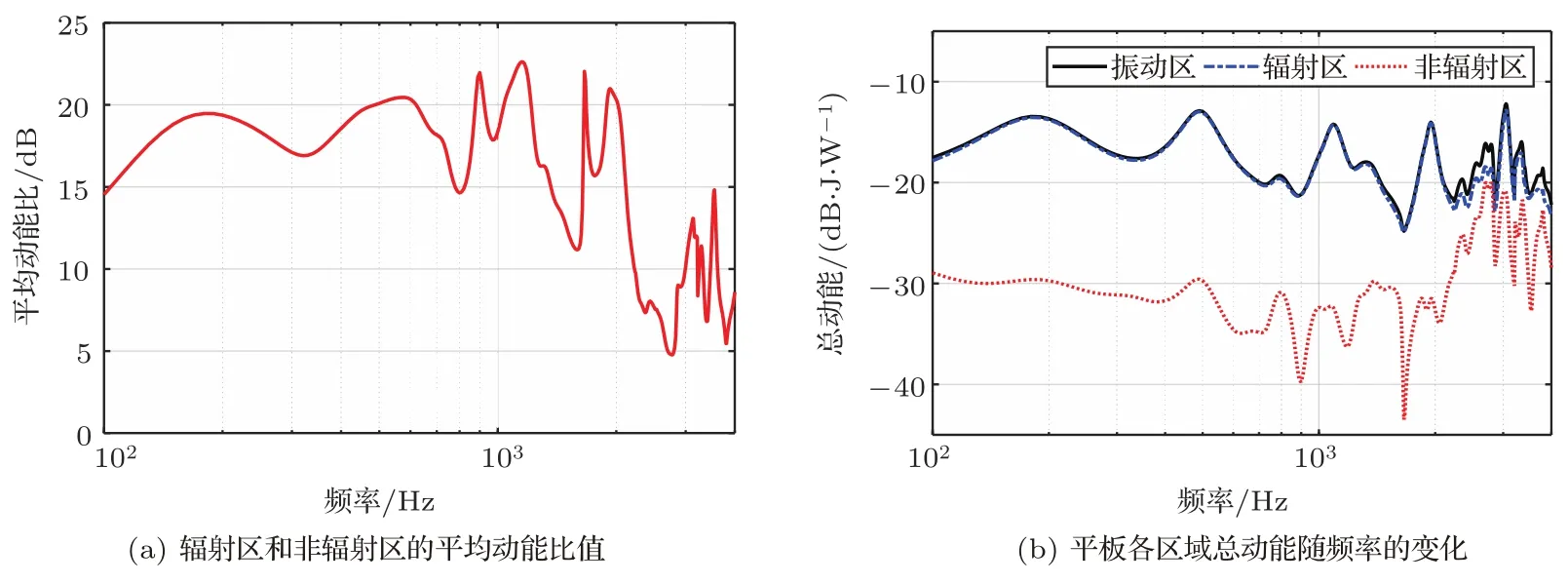
图5 平板振动局域化结果Fig.5 Results of the vibrational contrast control method

图6为不同频率处平板的动能分布(各子图利用所示频点测量点振幅的最大值对各测量点进行归一化)。平板的振动在各频点处均被局域在辐射区内。在低频段，辐射区各测量点振动速度同相位；在较高频段，由于VCC方法仅约束辐射区振动速度的幅值，所以辐射区内出现驻波，各测量点的振动速度同相或反相。

图6 单声道振动控制，不同频率下平板的归一化动能分布Fig.6 The distributions of the normalized kinetic energy at different frequencies for single channel vibration control

2.2 双声道振动控制

假设左声道的辐射区中心位置为(0.15la,0.50lb)，右声道中心位置为(0.85la,0.50lb)，两区域长宽均为0.30la和1.00lb。仿真中左右声道的辐射区分别辐射各自声道的声信号，且两声道的信号不相关。此时平板的振动分布如图7所示，其中左侧矩形框内区域为左辐射区，右侧矩形框内区域为右辐射区。在各频率处，左右声道声源分别被局域在平板的左右辐射区，并且较高频率时左右辐射区内均出现驻波。

图7 双声道振动控制，不同频率下平板的归一化动能分布Fig.7 The distributions of the normalized kinetic energy at different frequencies for stereo vibration control

3 实验验证

设计了一个平板扬声器用于验证本文方法的有效性。该扬声器采用矩形铝板作为振动薄板，其长宽分别为0.480 m和0.270 m，厚度为0.001 m；铝板四周利用不锈钢框架钳定以实现固支边界，如图8(a)所示。实验采用8个激振器，以铝板左下角为坐标原点，激振器A1∼A8的位置和仿真相同，坐标如表1所示。在长度x和宽度y方向，采样间隔均为0.040 m，采样点数分别为12和7，共计84个采样点。实验所用仪器包括Fireface UFX声卡、8通道功率放大器和PDV-100激光测振仪，实验设置如图8(b)所示。

图8 平板扬声器和实验设置示意图Fig.8 The prototype panel and the experimental setup

3.1 单声道振动控制

首先利用5 s长度的100 Hz∼4000 Hz线性扫频信号测量激振器到测量点的导纳函数。然后计算最大化右声道辐射区平均动能对应的最优滤波器qoR，其中辐射区中心位置为(0.408 m,0.135 m)，长宽分别为0.144 m和0.270 m。最后利用该滤波器在1/3倍频程的中心频率处验证算法的控制效果。图9为各频率处辐射区和非辐射区的平均动能比值以及平板总动能随频率的变化曲线。其中图9(a)中黑色虚线为不进行局域化控制的结果，此时8个激振器的输入信号相同。未控制时，在200 Hz∼4000 Hz辐射区和非辐射区的平均动能比值约为0 dB，平板的振动没有局域化效果。由于100 Hz时平板的振动主要由(1,1)和(1,3)模态决定，并且两模态的叠加使辐射区的振动较弱而非辐射区的振动较强，所以100 Hz时两区域的平均动能比为−10 dB。图9(a)中红色实线为局域化控制后的结果，在100 Hz∼4000 Hz的平均动能比值均有所提升，其中100 Hz∼2000 Hz的平均动能比值平均为12 dB。随着频率增加，控制效果有所下降。图9(b)为功放输出1 W功率时，局域化控制前后平板总动能随频率的变化。和仿真结果相同，VCC使平板的振动能量减小，其中低频的减小量大于高频。例如100 Hz∼500 Hz动能衰减约20 dB，500 Hz∼3000 Hz衰减约10 dB。图10为未局域化控制时平板动能的分布图，其中白色虚线内区域为辐射区，其他区域为非辐射区。低频时模态叠加较少，平板振动具有明显的模态特性，如图10(a)和图10(b)所示。频率较高时，由于MO较大，铝板振动比较复杂，如图10(e)和图10(f)所示。

图9 平板振动局域化结果Fig.9 Results of the vibrational contrast control method

图10 不进行局域化控制，不同频率下平板的归一化动能分布Fig.10 The distributions of the normalized energy at different frequencies for the case of without control

图11为单通道振动控制时平板动能的分布图。VCC使平板的振动被局域在辐射区内部。和仿真结果相同，低频时辐射区各测量点的振动速度相位相同，平板做类活塞式振动，如图11(a)和图11(b)所示；在较高频率时辐射区内出现驻波，如图11(c)所示。虽然频率较高时局域化控制的效果有所下降，但在3150 Hz处辐射区和非辐射区的平均动能比值仍有10 dB，如图9(a)所示，所以高频时VCC仍有较好的控制效果，如图11(f)所示。

3.2 双声道振动控制

由于平板振动满足线性叠加，左右声道声源的振动可以分别被局域在各自的辐射区内，进而实现立体声重放。假设左右声道的辐射区中心分别为(0.408 m,0.135 m)和(0.072 m,0.135 m)，长宽为0.144 m和0.270 m；两声道信号分别为θL和θR，并且两者不相关。分别计算局域化两声道信号的空间滤波器qoL和qoR，然后利用公式(17)得到8个激振器各自的输入信号。利用激光测振仪记录各测量点的振动速度，将记录的信号转换至频域得到不同频率下平板的动能分布，如图12所示。在各频点左右声道的声源均被局域在各自的辐射区内。低频时两辐射区的振动均类似活塞振动，如图12(a)和图12(b)所示；高频时两辐射区均出现驻波，如图12(c)和图12(d)所示。

图12 双声道振动控制时，不同频率下平板的归一化动能分布Fig.12 The distributions of the normalized kinetic energy at different frequencies for stereo channel vibration control

4 结论

本文利用振动对比度控制方法在矩形平板上实现了声源的局域化控制，并利用该方法实现了平板扬声器立体声重放的声源振动控制。实验表明，利用该方法可以在较宽的频带范围内实现声源的局域化控制，从而将左右声道的声源局域在平板扬声器的两侧。此外，包括本文方法在内的三种局域化控制方法均增加了平板的等效机械阻抗，从而使平板的动能减小。